Dropout NeuralNetworks
1.0.0
Dans ce projet de recherche, je me concentrerai sur les effets de l'évolution des taux d'abandon scolaire sur l'ensemble de données MNIST. Mon objectif est de reproduire la figure ci-dessous avec les données utilisées dans le document de recherche. Le but de ce projet est d'apprendre comment la figure d'apprentissage automatique a été produite. Plus précisément, se renseigner sur les effets sur l'erreur de classification lors de la modification/ne pas modifier la probabilité d'abandon.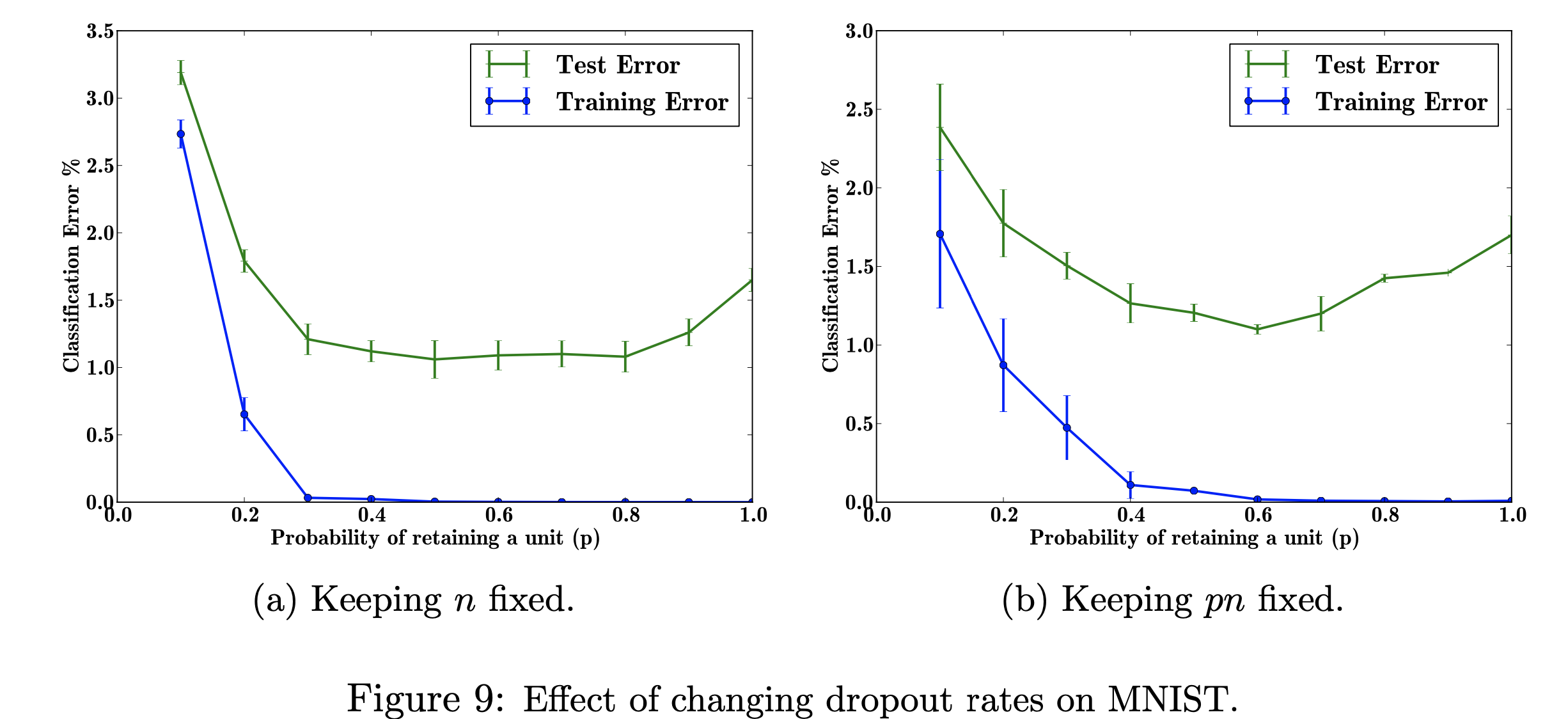
Figure référencée par : Srivastava, N., Hinton, G., Krizhevsky, A., Krizhevsky, I., Salakhutdinov, R., Dropout : un moyen simple d'empêcher le surapprentissage des réseaux neuronaux, Figure 9
J'ai utilisé TensorFlow pour exécuter le dropout sur l'ensemble de données MNIST, Matplotlib pour aider à recréer la figure dans le document. J'ai également utilisé une bibliothèque décimale intégrée pour calculer les différentes valeurs de p, de 0,0 à 1,0. La bibliothèque "csv" a été importée pour ajouter des données précédemment exécutées dans un fichier CSV, afin de gagner du temps dans le calcul des valeurs de p déjà calculées. Numpy a été importé pour que le tracé ait la même taille de pas sur les axes x et y. Enfin, j'ai importé "os" afin de pouvoir me débarrasser d'une erreur due à l'utilisation d'un CPU plutôt que d'un GPU.
Explorer les effets des valeurs variables de l'hyperparamètre réglable « p » (la probabilité de conserver une unité dans le réseau) et du nombre de couches cachées, « n », qui affectent les taux d'erreur. Lorsque le produit de p et n est fixe, nous pouvons voir que l'ampleur de l'erreur pour les petites valeurs de p a diminué (fig. 9a) par rapport au maintien constant du nombre de couches cachées (fig. 9b).
Avec des données d'entraînement limitées, de nombreuses relations complexes entre entrées/sorties seront le résultat du bruit d'échantillonnage. Ils existeront dans l'ensemble d'apprentissage, mais pas dans les données de test réelles, même si elles proviennent de la même distribution. Cette complication conduit à un surapprentissage, c'est l'un des algorithmes permettant d'éviter que cela ne se produise. L'entrée de cette figure est un ensemble de données de chiffres manuscrits, et le résultat après l'ajout de l'abandon sont différentes valeurs qui décrivent le résultat de l'application de la méthode d'abandon. Dans l’ensemble, il y a moins d’erreurs après l’ajout d’un abandon.
Un problème réel auquel cela peut s'appliquer est la recherche sur Google, quelqu'un peut rechercher un titre de film, mais il se peut qu'il ne recherche que des images parce qu'il apprend davantage visuellement. Ainsi, supprimer les parties textuelles ou de brèves explications vous aidera à vous concentrer sur les caractéristiques de l'image. L'article indique d'où ils récupèrent les données (http://yann.lecun.com/exdb/mnist/). Chaque image est une représentation de 28 x 28 chiffres. Les étiquettes y semblent être les colonnes de données d'image.
Mon objectif en reproduisant cette figure est de tester/entraîner les données et de calculer l'erreur de classification pour chaque probabilité de p (probabilité de conserver une unité dans le réseau). Mon objectif est d'augmenter p à mesure que l'erreur diminue pour montrer que mon implémentation est valide, et j'ajusterai cet hyper paramètre pour obtenir le même résultat. Je ferai cela en parcourant toutes les données de formation et de test en utilisant une architecture 784-2048-2048-2048-10 et en gardant le n fixe, puis en modifiant le pn pour qu'il soit corrigé. Je rassemblerai/écrirai ensuite les données dans un fichier csv. Ce fichier csv contiendra alors toutes les données nécessaires pour sortir les chiffres. Dans ce projet, j'apprendrai comment le taux d'abandon peut profiter à l'erreur globale dans un réseau neuronal.
Cliquez pour voir
