Résout le puzzle de la Tour de Hanoï par apprentissage par renforcement.
Dans un environnement Python avec Numpy et Pandas installés, exécutez le script hanoi.py pour produire les trois tracés affichés dans la section Résultats. Le script peut facilement être adapté pour jouer au jeu avec un nombre de disques N différent, par exemple.
L'apprentissage par renforcement a récemment suscité un regain d'intérêt avec le passage à tabac d'un joueur de Go humain professionnel par AlphaGo de Google Deepmind. Ici, un casse-tête plus simple est résolu : le jeu de la Tour de Hanoï. L'implémentation suit l'algorithme Q-learning proposé initialement par Watkins & Dayan [1].
Le jeu Tower of Hanoi se compose de trois piquets et d'un certain nombre de disques de différentes tailles qui peuvent glisser sur les piquets. Le puzzle commence avec tous les disques empilés sur le premier piquet par ordre croissant, le plus grand en bas et le plus petit en haut. L'objectif du jeu est de déplacer tous les disques vers le troisième pion. Les seuls mouvements légaux sont ceux qui font passer le disque le plus haut d'un plot à un autre, avec la restriction qu'un disque ne peut jamais être placé sur un disque plus petit. La figure 1 montre la solution optimale pour 4 disques.

Figure 1. Une solution animée du puzzle de la Tour de Hanoï pour 4 disques. (Source : Wikipédia).
À la suite d'Anderson [2], nous représentons l'état du jeu par des tuples, où le i ème élément indique sur quelle cheville se trouve le i ème disque. Les disques sont étiquetés par ordre croissant de taille. Ainsi, l'état initial est (111) et l'état final souhaité est (333) (Figure 2).
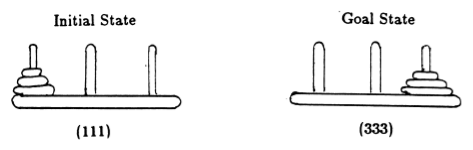
Figure 2. États initiaux et objectifs du puzzle Tour de Hanoï avec 3 disques. (De [2]).
Les états du puzzle et les transitions entre eux correspondant aux mouvements légaux forment le graphique de transition d'état du puzzle, illustré à la figure 3.
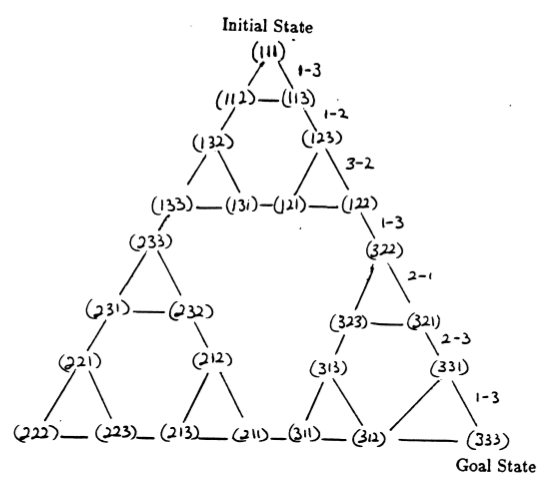
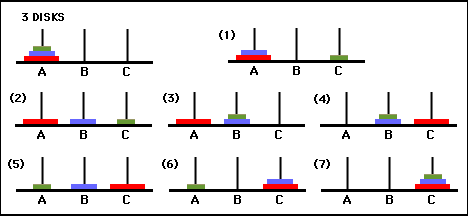
Figure 3. Graphique de transition d'état pour le puzzle à trois disques de la Tour de Hanoï (ci-dessus) et la solution optimale correspondante en 7 mouvements (ci-dessous), qui suit le chemin du côté droit du graphique. (De [2] et Mathforum.org).
Le nombre minimum de mouvements requis pour résoudre un puzzle de la Tour de Hanoï est de 2 N - 1, où N est le nombre de disques. Ainsi, pour N = 3, le puzzle peut être résolu en 7 mouvements, comme le montre la figure 3. Dans la section suivante, nous décrivons comment cela est réalisé par le Q-learning.
R et la matrice 'valeur d'action' Q pour 2 disques La première étape du programme consiste à générer une matrice de récompense R qui capture les règles du jeu et donne une récompense en cas de victoire. Par souci de simplicité, la matrice de récompense est présentée pour N = 2 disques dans la figure 4.
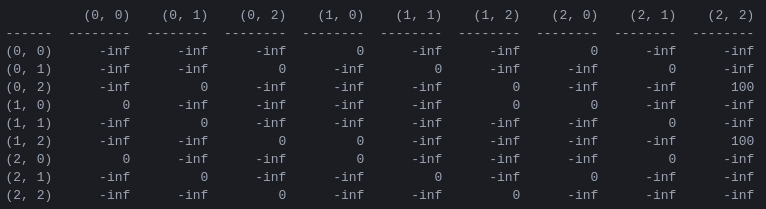
Figure 4. Matrice de récompense R pour un puzzle Tour de Hanoï avec N = 2 disques. Le ( i , j )ème élément représente la récompense pour le passage de l'état i à j . Les états sont étiquetés par des tuples comme dans les figures 2 et 3, à la différence que les piquets sont indexés « pythoniquement » de 0 à 2 plutôt que de 1 à 3. Les mouvements qui mènent à l'état objectif (2,2) se voient attribuer une récompense. de 100, les mouvements illégaux de , et tous les autres mouvements de 0.
La matrice de récompense R ne décrit que les récompenses immédiates : une récompense de 100 ne peut être obtenue qu'à partir des avant-derniers états (0,2) et (1,2). Dans les autres États, chacun des 2 ou 3 mouvements possibles a une récompense égale de 0, et il n'y a aucune raison apparente de choisir l'un plutôt que l'autre.
En fin de compte, nous cherchons à attribuer une « valeur » à chaque mouvement possible dans chaque état, de sorte qu'en maximisant ces valeurs, nous puissions définir une politique menant à la solution optimale. La matrice de « valeurs » pour chaque action dans chaque état est appelée Q et peut être résolue de manière récursive, ou « apprise », de manière stochastique comme décrit par Watkins & Dayan [1]. Le résultat pour 2 disques est présenté dans la figure 5.
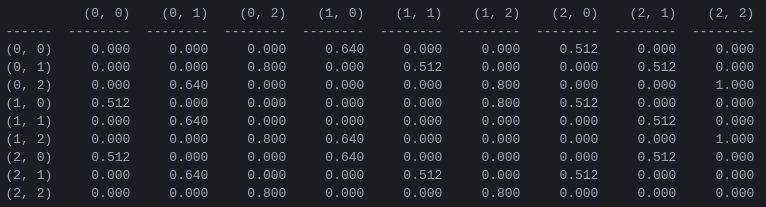
Figure 5. Matrice Q de « valeur d'action » pour le jeu Tower of Hanoi avec 2 disques, appris avec un facteur d'actualisation de = 0,8, un facteur d'apprentissage = 1,0 et 1 000 épisodes d'entraînement.
Les valeurs de la matrice Q sont essentiellement des poids qui peuvent être attribués aux sommets du graphe de transition d'état de la figure 3, qui guident l'agent de l'état initial à l'état objectif de la manière la plus courte possible. Dans cet exemple, en commençant à l'état (0,0) et en choisissant successivement le mouvement avec la valeur de Q la plus élevée, le lecteur peut se convaincre que la matrice Q guide l'agent à travers la séquence d'états (0,0) - (1 ,0) - (1,2) - (2,2), ce qui correspond à la solution optimale en 3 coups du jeu à 2 disques de la Tour de Hanoï (Figure 6).
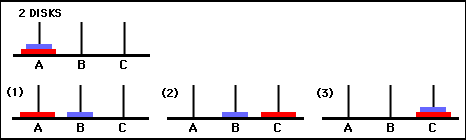
Figure 6. Solution du jeu Tour de Hanoï avec 2 disques. Les états consécutifs sont représentés respectivement par (0,0), (1,0), (1,2) et (2,2). (Source : mathforum.org).
Dans cet exemple où la matrice Q a convergé vers sa valeur optimale, elle définit une politique stationnaire : chaque ligne contient une action avec une valeur maximale unique. Cependant, au cours du processus d’apprentissage, différentes actions peuvent avoir la même valeur de Q . (En particulier, c'est le cas au début de l'entraînement lorsque Q est initialisé à une matrice de zéros). Dans les simulations présentées dans la section suivante, de telles situations sont traitées par la politique stochastique suivante : dans les cas où la valeur Q maximale est partagée entre plusieurs actions, choisir une de ces actions au hasard.
Les performances de l'algorithme Q-learning peuvent être mesurées en comptant le nombre de mouvements nécessaires (en moyenne) pour résoudre le puzzle de la Tour de Hanoï. Ce nombre diminue avec le nombre d'épisodes d'entraînement jusqu'à atteindre finalement la valeur optimale 2 N - 1, où N est le nombre de disques, comme illustré sur la figure 7 pour N = 2, 3 et 4.
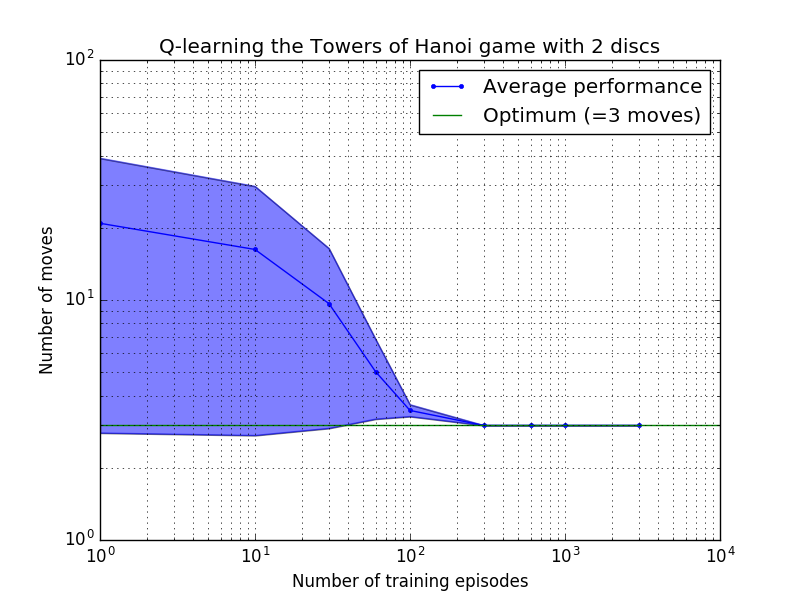
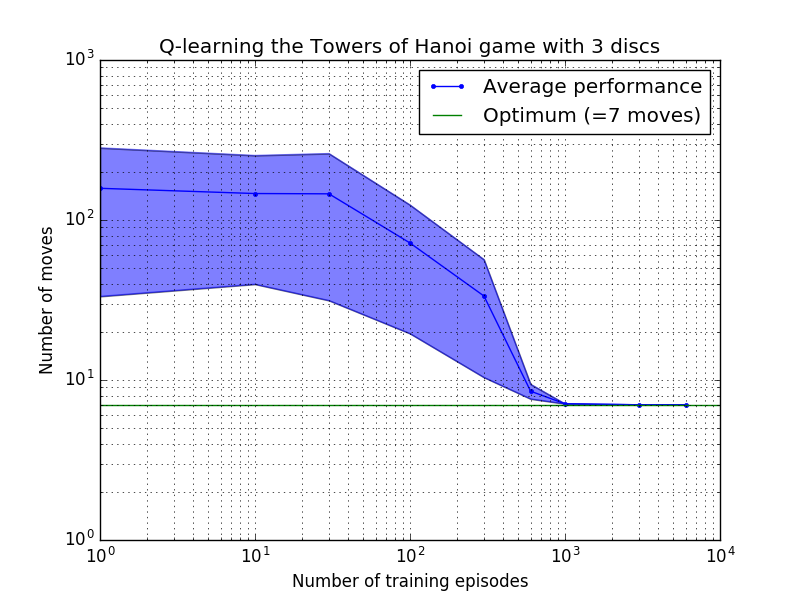
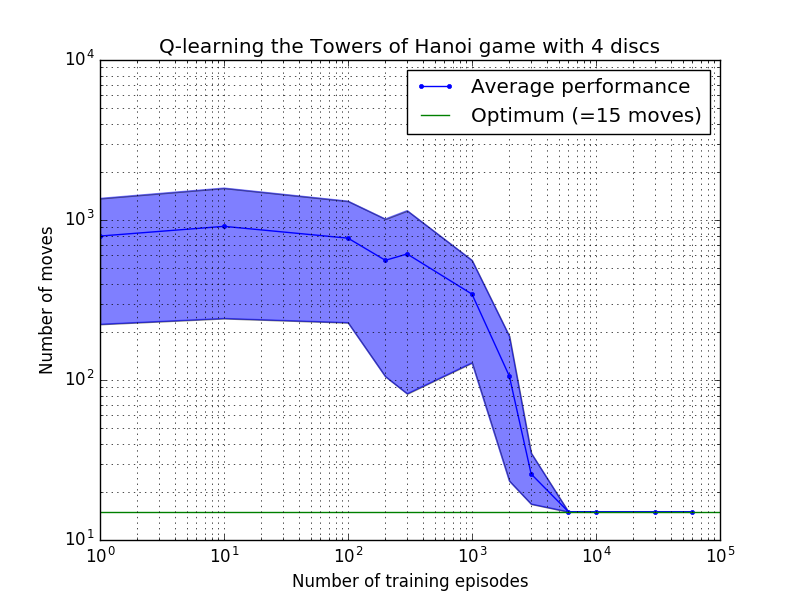
Figure 7. Performances de l'algorithme Q-learning pour le jeu Tower of Hanoi avec, de haut en bas, 2, 3 et 4 disques. Dans tous les cas, l'apprentissage a été réalisé avec un facteur d'actualisation de = 0,8 et un facteur d'apprentissage de = 1,0. La courbe bleue continue représente la performance moyenne sur 100 époques d'entraînement et de jeu 100 fois pour chaque politique stochastique résultante. Les limites supérieure et inférieure de la zone ombrée en bleu sont décalées par rapport à la moyenne de l'écart type estimé. (Pour N = 3 et N = 4, le nombre d'épisodes d'entraînement et de temps de jeu ont été réduits à 10 et 10, respectivement, en raison de contraintes informatiques).
Une caractéristique intéressante des caractéristiques d'apprentissage de la figure 7 est que dans tous les cas, l'apprentissage est lent au départ, et l'agent ne fait guère mieux que la politique de « formation zéro » consistant à choisir des mouvements au hasard. À un moment donné, l'apprentissage atteint un « point d'inflexion », puis converge vers le nombre optimal de mouvements à un rythme accéléré (bien que cela soit quelque peu exagéré par l'échelle logarithmique).
Un script Python résout avec succès le puzzle de la Tour de Hanoï de manière optimale pour n'importe quel nombre de disques grâce à Q-learning. Le script peut être facilement adapté à d'autres problèmes avec une matrice de récompense R différente.
Le nombre d'épisodes d'entraînement nécessaires pour converger vers une solution optimale augmente fortement avec le nombre de disques N : pour N=2 disques il faut environ 300 épisodes, alors que pour N=4 il en faut environ 6 000. Une amélioration possible de l'algorithme d'apprentissage serait de lui permettre de rechercher automatiquement des solutions récursives, comme l'a fait Hengst [3].
[ 1 ] Watkins & Dayan, Q-learning , Machine Learning, 8, 279-292 (1992). (PDF).
[ 2 ] Anderson, Apprentissage et résolution de problèmes avec les systèmes connexionnistes multicouches , Ph.D. thèse (1986). (PDF).
[ 3 ] Hengst, Discovering Hierarchy in Reinforcement Learning with HEXQ , Actes de la dix-neuvième conférence internationale sur l'apprentissage automatique (2002). (PDF).