
Mojo — un nouveau langage de programmation pour tous les développeurs, scientifiques IA/ML et ingénieurs logiciels.
Une liste organisée de superbes codes Mojo, de résolution de problèmes, de solutions et, à l'avenir, de bibliothèques, de frameworks, de logiciels et de ressources.
Accumulons ici des connaissances technologiques très récentes et les meilleures pratiques.
Mojo est un langage de programmation qui combine la convivialité de Python avec les capacités de performances de C++ et Rust. De plus, Mojo permet aux utilisateurs d'exploiter le vaste écosystème de bibliothèques Python.
En bref
Mojo est un nouveau langage de programmation qui comble le fossé entre la recherche et la production en combinant le meilleur de la syntaxe Python avec la programmation système et la métaprogrammation.
hello.mojo ou hello. l'extension du fichier peut être un emoji !
Vous pouvez en savoir plus sur pourquoi Modular fait cela Pourquoi Mojo
Ce que nous voulions, c'était un modèle de programmation innovant et évolutif, capable de cibler les accélérateurs et autres systèmes hétérogènes omniprésents dans le domaine de l'IA. ... Les systèmes d'IA appliquée doivent résoudre tous ces problèmes, et nous avons décidé qu'il n'y avait aucune raison pour que cela ne puisse pas être fait avec un seul langage. Ainsi, Mojo est né.
Mais Python a très bien fait son travail =)
Nous n'avons pas vu la nécessité d'innover dans la syntaxe du langage ou dans la communauté. Nous avons donc choisi d'adopter l'écosystème Python parce qu'il est très largement utilisé, qu'il est apprécié par l'écosystème de l'IA et parce que nous pensons que c'est un langage vraiment sympa.
Mojo signifie « un charme magique » ou « des pouvoirs magiques ». Nous avons pensé que c'était un nom approprié pour un langage qui apporte des pouvoirs magiques à Python :python:, notamment en ouvrant un modèle de programmation innovant pour les accélérateurs et autres systèmes hétérogènes omniprésents dans l'IA aujourd'hui.
Guido van Rossum, dictateur bienveillant à vie et Christopher Arthur Lattner, inventeur distingué, créateur et leader bien connu de la prononciation Mojo =)
Selon le descriptif
Qui sait, ces langages de programmation seront très heureux, car Mojo bénéficie de formidables enseignements tirés des autres langages Rust, Swift, Julia, Zig, Nim, etc.
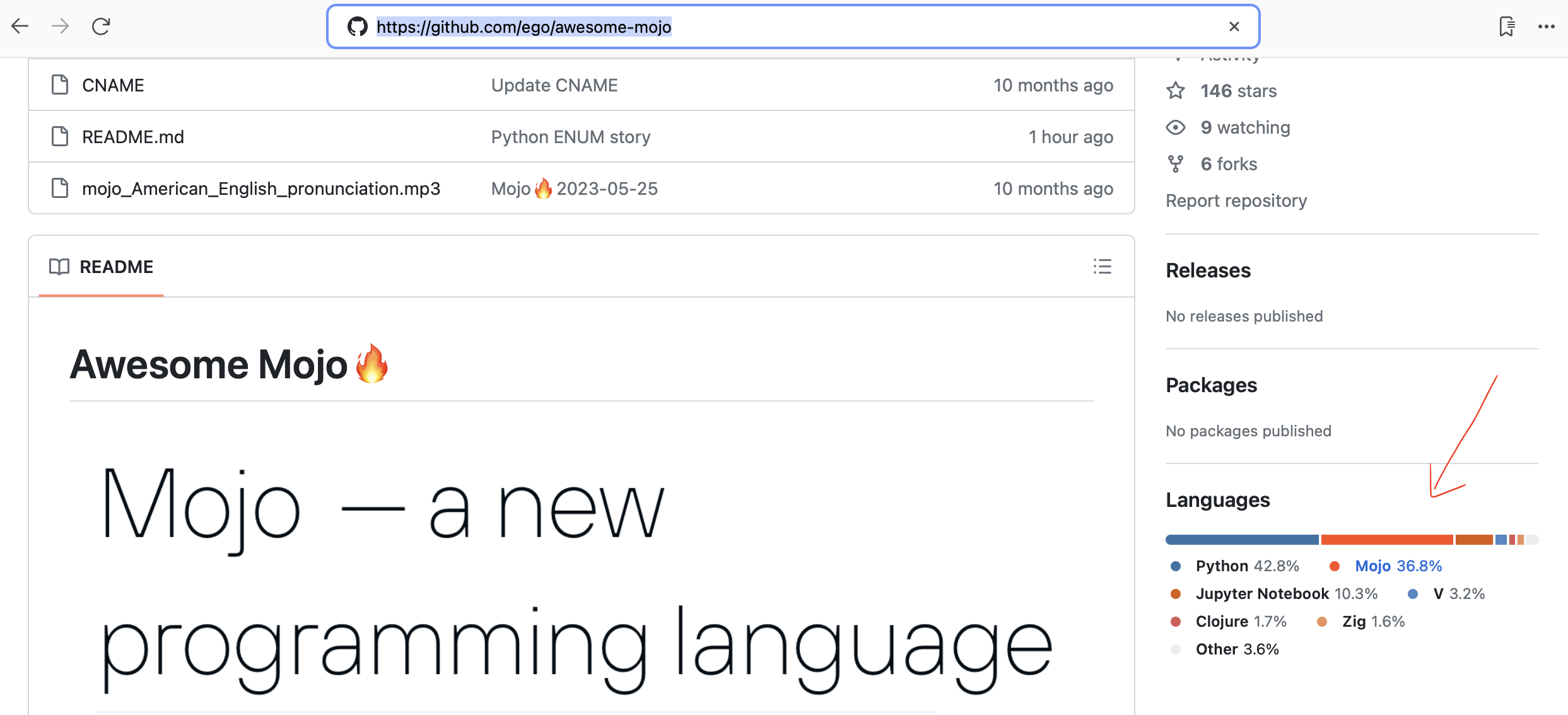
[nouveau]
Github détecte désormais automatiquement le code Mojo !
Framework HTTP simple et rapide pour Mojo ! Parfait pour créer des services Web et des API simples. Pour les Mojiciens
Cadre d'analyse comparative des implémentations LLama
Traduction automatisée du code Python vers Mojo
Recherche sur les bases de données des langages de programmation
19 octobre 2023 Mojo est désormais disponible sur Mac ! Utiliser la console développeur
Chris Lattner : L'avenir de la programmation et de l'IA | Podcast Lex Fridman #381
Explication du système de types Mojo et Python | Chris Lattner et Lex Fridman
Mojo peut-il exécuter du code Python ? | Chris Lattner et Lex Fridman
Passer de Python au langage de programmation Mojo | Chris Lattner et Lex Fridman
Nouveau sujet GitHub mojo-lang. Vous pouvez donc le suivre.
Guido van Rossum à propos de Mojo = Python avec performances C++/GPU ?
Structure Tensor avec quelques opérations de base #251
Matrice fn avec numpy #267
Mises à jour sur les fermetures lambda et parameter et les fonctions d'ordre supérieur dans mojo #244
25 mai 2023, Guido van Rossum (gvanrossum#8415), créateur et émérite BDFL de Python, visitez le chat Discord public Mojo
En attente d'une coloration syntaxique Mojo sur GitHub
Nouvelle version Mojo 2023-05-24
[vieux]
Mojo
brew install hyperfinebrew install macchinapip3 install numpy matplotlib scipybrew install silicon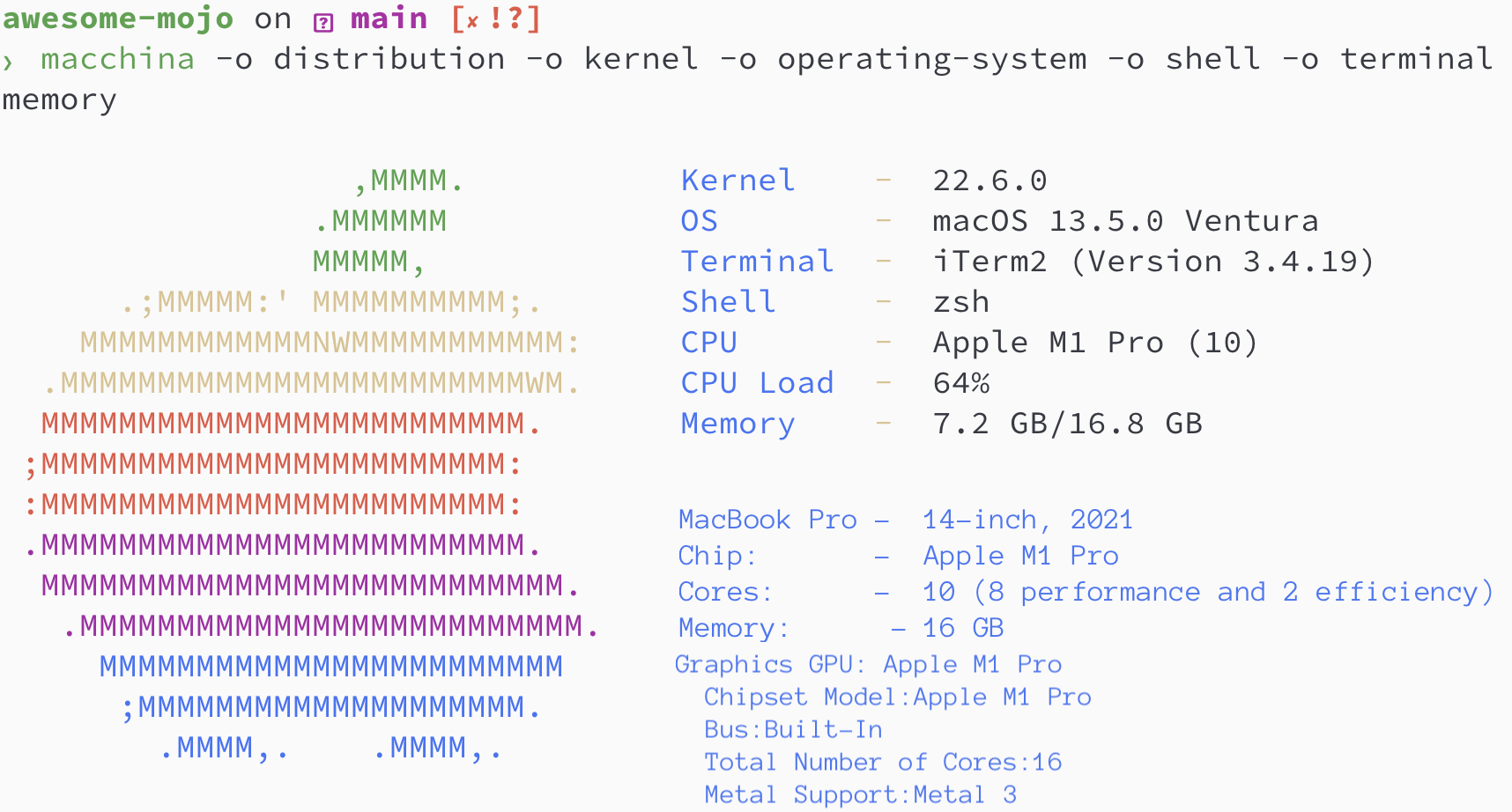
Versions Python / Mojo / Codon / Rust
> python3 --version
Python 3.11.6
> mojo --version
mojo 0.4.0 (9e33b013)
> codon --version
0.16.3
> rustc --version
rustc 1.65.0-nightly (9243168fa 2022-08-31)Trouvons la séquence de Fibonacci où
N = 100
def fibonacci_recursion ( n ):
return n if n < 2 else fibonacci_recursion ( n - 1 ) + fibonacci_recursion ( n - 2 )
fibonacci_recursion ( 100 )hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json python_recursion.json ' python3 benchmarks/fibonacci_sequence/python_recursion.py 'RESULTAT : TIMEOUT, j'ai annulé le calcul après 1 min
def fibonacci_iteration ( n ):
a , b = 0 , 1
for _ in range ( n ):
a , b = b , a + b
return a
fibonacci_iteration ( 100 )hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/python_iteration.json ' python3 benchmarks/fibonacci_sequence/python_iteration.py ' RÉSULTAT :
Benchmark 1 : python3 benchmarks/fibonacci_sequence/python_iteration.py
Temps (moyenne ± σ) : 16 374,7 µs ± 904,0 µs [Utilisateur : 11 483,5 µs, Système : 3 680,0 µs]
Plage (min … max): 15 361,0 µs … 22 863,3 µs 100 exécutions
python3 -m compileall benchmarks/fibonacci_sequence/python_recursion.py
python3 -m compileall benchmarks/fibonacci_sequence/python_iteration.pyhyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/python_recursion.cpython-311.json ' python3 benchmarks/fibonacci_sequence/__pycache__/python_recursion.cpython-311.pyc '
# TIMEOUT!
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/python_iteration.cpython-311.json ' python3 benchmarks/fibonacci_sequence/__pycache__/python_iteration.cpython-311.pyc ' RÉSULTAT :
Benchmark 1 : python3 benchmarks/fibonacci_sequence/ pycache /python_iteration.cpython-311.pyc
Temps (moyenne ± σ) : 16 584,6 µs ± 761,5 µs [Utilisateur : 11 451,8 µs, Système : 3 813,3 µs]
Plage (min … max): 15 592,0 µs … 20 953,2 µs 100 exécutions
fn fibonacci_recursion ( n : Int) -> Int:
return n if n < 2 else fibonacci_recursion(n - 1 ) + fibonacci_recursion(n - 2 )
fn main ():
_ = fibonacci_recursion( 100 )hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/mojo_recursion.json ' mojo run benchmarks/fibonacci_sequence/mojo_recursion.mojo 'RESULTAT : TIMEOUT, j'ai annulé le calcul après 1 min
fn fibonacci_iteration ( n : Int) -> Int:
var a : Int = 0
var b : Int = 1
for _ in range (n):
a = b
b = a + b
return a
fn main ():
_ = fibonacci_iteration( 100 )hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/mojo_iteration.json ' mojo run benchmarks/fibonacci_sequence/mojo_iteration.mojo ' RÉSULTAT :
Benchmark 1 : mojo run benchmarks/fibonacci_sequence/mojo_iteration.mojo
Temps (moyenne ± σ) : 43 852,7 µs ± 1 353,5 µs [Utilisateur : 38 156,0 µs, Système : 10 407,3 µs]
Plage (min … max): 42 033,6 µs … 49 357,3 µs 100 exécutions
mojo build benchmarks/fibonacci_sequence/mojo_recursion.mojo
mojo build benchmarks/fibonacci_sequence/mojo_iteration.mojohyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/mojo_recursion.exe.json ' ./benchmarks/fibonacci_sequence/mojo_recursion '
# TIMEOUT!
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/mojo_iteration.exe.json ' ./benchmarks/fibonacci_sequence/mojo_iteration ' RÉSULTAT :
Référence 1 : ./benchmarks/fibonacci_sequence/mojo_iteration
Temps (moyenne ± σ) : 934,6 µs ± 468,9 µs [Utilisateur : 409,8 µs, Système : 247,8 µs]
Plage (min … max): 552,7 µs … 4522,9 µs 100 exécutions
def fibonacci_recursion(n):
return n if n < 2 else fibonacci_recursion(n - 1) + fibonacci_recursion(n - 2)
fibonacci_recursion(100)
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/codon_recursion.json ' codon run --release benchmarks/fibonacci_sequence/codon_recursion.codon 'RESULTAT : TIMEOUT, j'ai annulé le calcul après 1 min
def fibonacci_iteration(n):
a, b = 0, 1
for _ in range(n):
a, b = b, a+b
return a
fibonacci_iteration(100)
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/codon_iteration.json ' codon run --release benchmarks/fibonacci_sequence/codon_iteration.codon ' RÉSULTAT :
Benchmark 1 : codon run --release benchmarks/fibonacci_sequence/codon_iteration.codon
Temps (moyenne ± σ) : 628060,1 µs ± 10430,5 µs [Utilisateur : 584524,3 µs, Système : 39358,5 µs]
Plage (min … max): 612742,5 µs … 662716,9 µs 100 exécutions
codon build --release -exe benchmarks/fibonacci_sequence/codon_recursion.codon
codon build --release -exe benchmarks/fibonacci_sequence/codon_iteration.codonhyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json codon_recursion.exe.json ' ./benchmarks/fibonacci_sequence/codon_recursion '
# TIMEOUT!
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/codon_iteration.exe.json ' ./benchmarks/fibonacci_sequence/codon_iteration ' RÉSULTAT :
Référence 1 : ./benchmarks/fibonacci_sequence/codon_iteration
Temps (moyenne ± σ) : 2 732,7 µs ± 1 145,5 µs [Utilisateur : 1 466,0 µs, Système : 1 061,5 µs]
Plage (min … max): 2036,6 µs … 13236,3 µs 100 exécutions
fn fibonacci_recursive ( n : i64 ) -> i64 {
if n < 2 {
return n ;
}
return fibonacci_recursive ( n - 1 ) + fibonacci_recursive ( n - 2 ) ;
}
fn main ( ) {
let _ = fibonacci_recursive ( 100 ) ;
} rustc -C opt-level=3 benchmarks/fibonacci_sequence/rust_recursion.rs -o benchmarks/fibonacci_sequence/rust_recursion
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/rust_recursion.json ' ./benchmarks/fibonacci_sequence/rust_recursion 'RESULTAT : TIMEOUT, j'ai annulé le calcul après 1 min
fn fibonacci_iteration ( n : usize ) -> usize {
let mut a = 1 ;
let mut b = 1 ;
for _ in 1 ..n {
let old = a ;
a = b ;
b += old ;
}
b
}
fn main ( ) {
let _ = fibonacci_iteration ( 100 ) ;
} rustc -C opt-level=3 benchmarks/fibonacci_sequence/rust_iteration.rs -o benchmarks/fibonacci_sequence/rust_iteration
hyperfine --warmup 10 -r 100 --time-unit=microsecond --export-json benchmarks/fibonacci_sequence/rust_iteration.json ' ./benchmarks/fibonacci_sequence/rust_iteration ' RÉSULTAT :
Référence 1 : ./benchmarks/fibonacci_sequence/rust_iteration
Temps (moyenne ± σ) : 848,9 µs ± 283,2 µs [Utilisateur : 371,8 µs, Système : 261,4 µs]
Plage (min … max): 525,9 µs … 2607,3 µs 100 courses
# Merge all JSON files into benchmarks.json
python3 benchmarks/hyperfine-scripts/merge_jsons.py benchmarks/fibonacci_sequence/ benchmarks/fibonacci_sequence/benchmarks.json
python3 benchmarks/hyperfine-scripts/plot2.py benchmarks/fibonacci_sequence/benchmarks.json
python3 benchmarks/hyperfine-scripts/plot3.py benchmarks/fibonacci_sequence/benchmarks.json
python3 benchmarks/hyperfine-scripts/advanced_statistics.py benchmarks/fibonacci_sequence/benchmarks.json > benchmarks/fibonacci_sequence/benchmarks.json.md
silicon benchmarks/fibonacci_sequence/benchmarks.json.md -l python -o benchmarks/fibonacci_sequence/benchmarks.json.md.pngStatistiques avancées
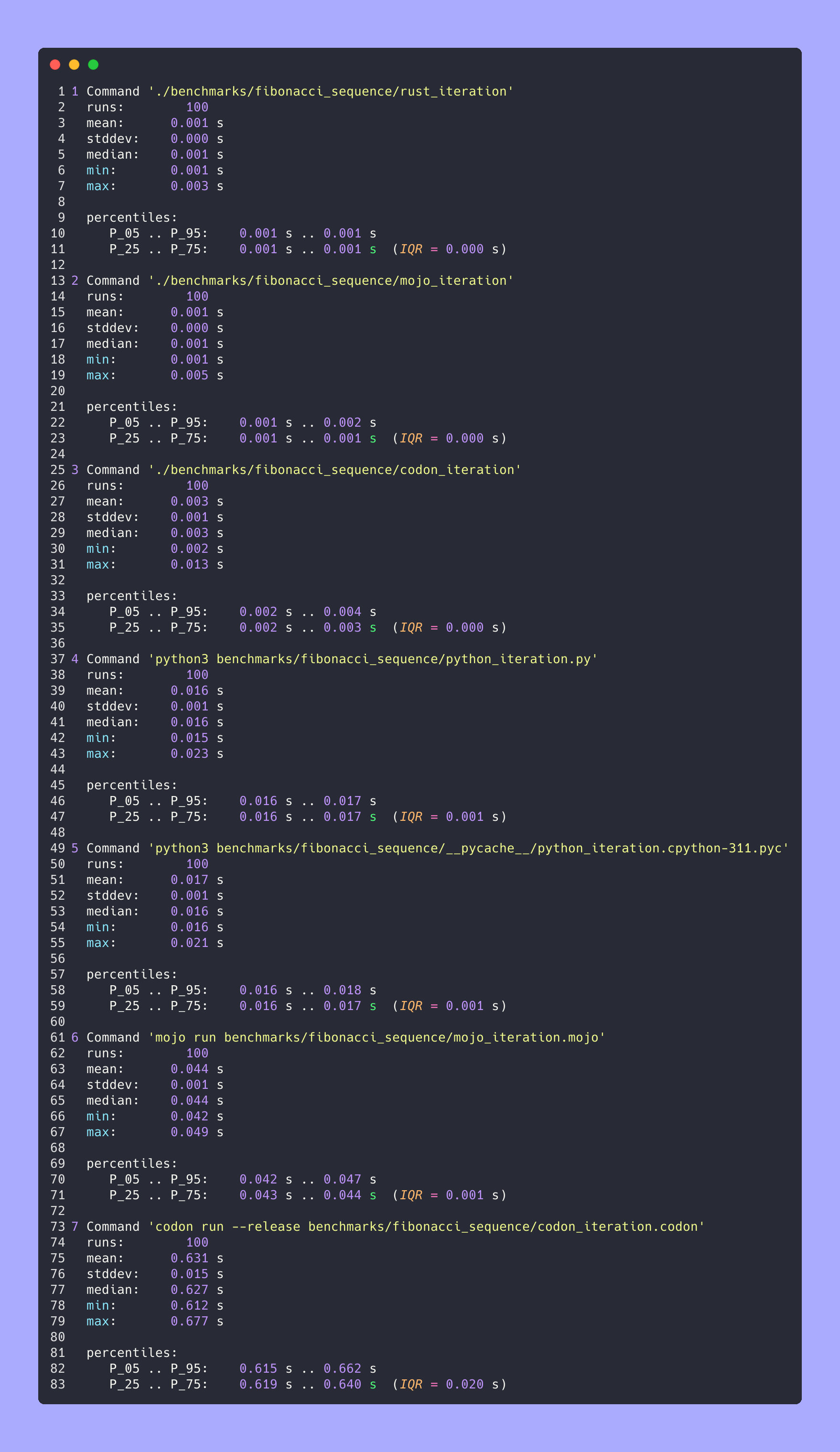
Tous ensemble
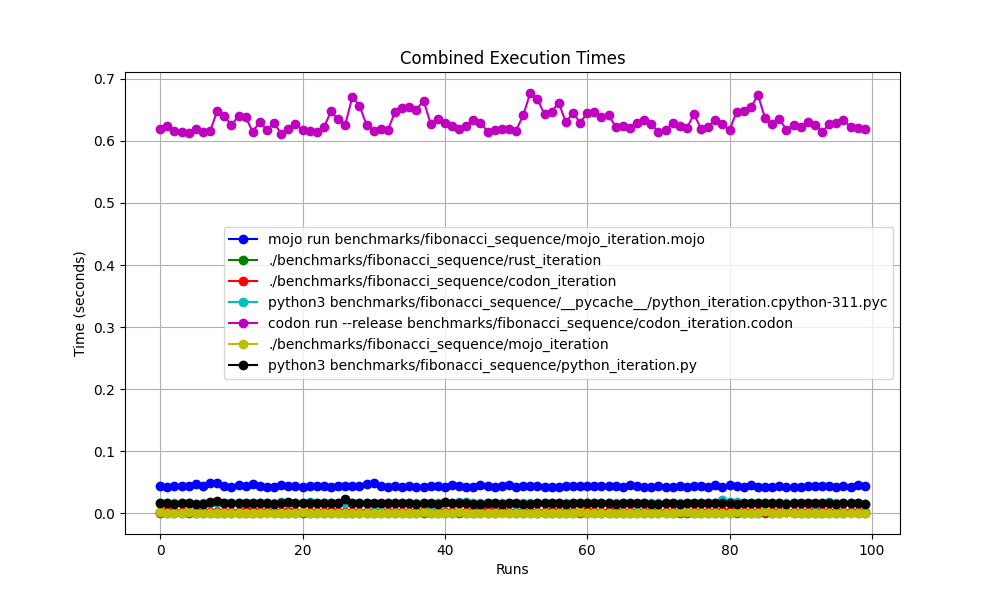
Zoomé
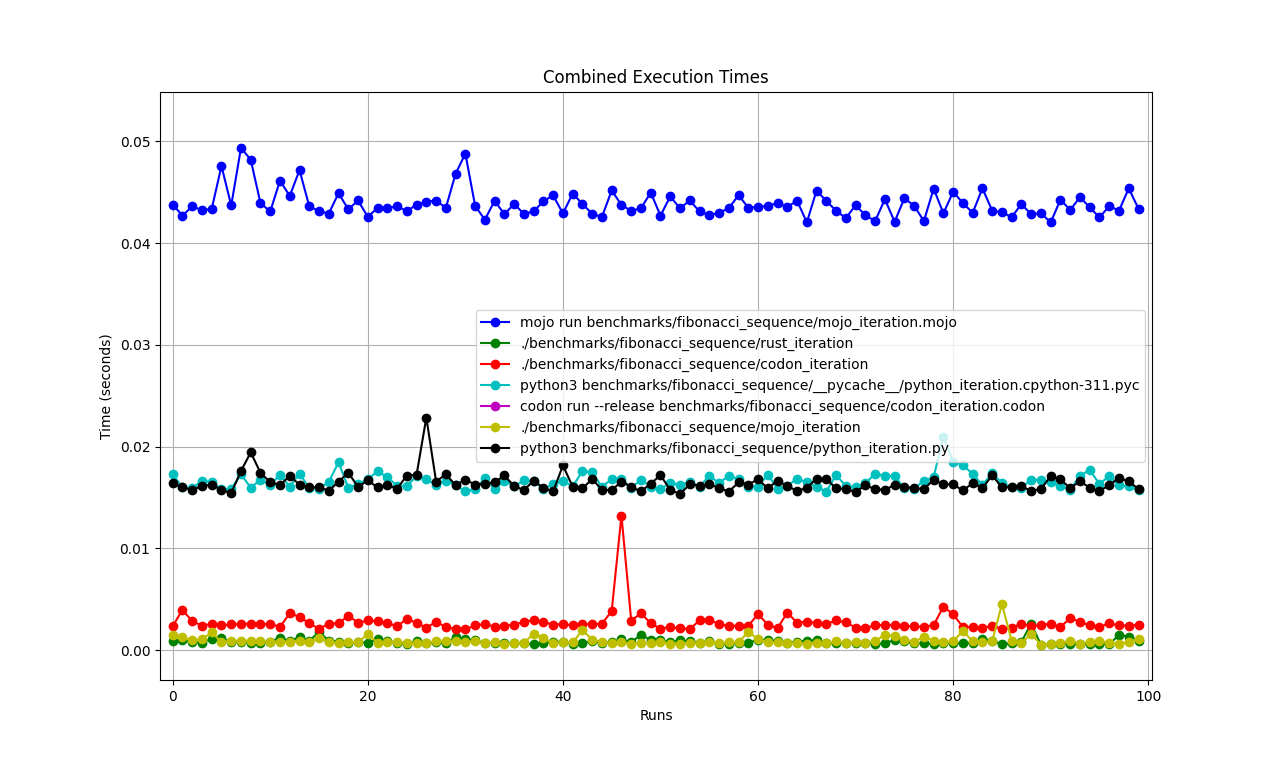
Détaillé un par un
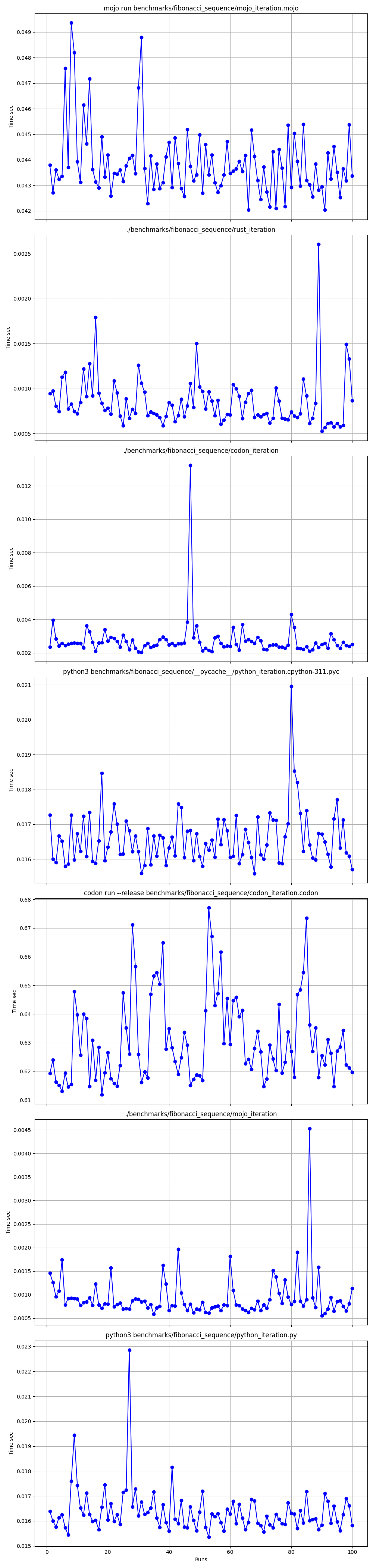
Lieux
Mais ici beaucoup de questions :
mojo run si lentement ?codon run --release est-il si lent ?run interpréteur Python plus rapide que Mojo/Codon ?On peut donc dire que Mojo est aussi rapide que Rust sur Mac !
Trouvons Mandelbrot Set où
LARGEUR = 960
HAUTEUR = 960
MAX_ITERS = 200
MIN_X = -2,0
MAX_X = 0,6
MIN_Y = -1,5
MAX_Y = 1,5
def mandelbrot_kernel ( c ):
z = c
for i in range ( MAX_ITERS ):
z = z * z + c # Change this for different Multibrot sets (e.g., 2 for Mandelbrot)
if z . real * z . real + z . imag * z . imag > 4 :
return i
return MAX_ITERS
def compute_mandelbrot ():
t = [[ 0 for _ in range ( WIDTH )] for _ in range ( HEIGHT )] # Pixel matrix
dx = ( MAX_X - MIN_X ) / WIDTH
dy = ( MAX_Y - MIN_Y ) / HEIGHT
for row in range ( HEIGHT ):
for col in range ( WIDTH ):
t [ row ][ col ] = mandelbrot_kernel ( complex ( MIN_X + col * dx , MIN_Y + row * dy ))
return t
compute_mandelbrot ()python3 -m compileall benchmarks/multibrot_set/multibrot.py
hyperfine --warmup 10 -r 10 --time-unit=microsecond --export-json benchmarks/multibrot_set/multibrot.cpython-311.json ' python3 benchmarks/multibrot_set/__pycache__/multibrot.cpython-311.pyc ' RÉSULTAT :
Benchmark 1 : python3 benchmarks/multibrot_set/ pycache /multibrot.cpython-311.pyc
Temps (moyenne ± σ) : 5444155,4 µs ± 23059,7 µs [Utilisateur : 5419790,1 µs, Système : 18131,3 µs]
Plage (min … max): 5408155,3 µs … 5490548,4 µs 10 exécutions
Version Mojo sans optimisation.
# Compute the number of steps to escape.
def multibrot_kernel ( c : ComplexFloat64) -> Int:
z = c
for i in range ( MAX_ITERS ):
z = z * z + c # Change this for different Multibrot sets (e.g., 2 for Mandelbrot)
if z.squared_norm() > 4 :
return i
return MAX_ITERS
def compute_multibrot () -> Tensor[FloatType]:
# create a matrix. Each element of the matrix corresponds to a pixel
t = Tensor[FloatType]( HEIGHT , WIDTH )
dx = ( MAX_X - MIN_X ) / WIDTH
dy = ( MAX_Y - MIN_Y ) / HEIGHT
y = MIN_Y
for row in range ( HEIGHT ):
x = MIN_X
for col in range ( WIDTH ):
t[Index(row, col)] = multibrot_kernel(ComplexFloat64(x, y))
x += dx
y += dy
return t
_ = compute_multibrot()mojo build benchmarks/multibrot_set/multibrot.mojo
hyperfine --warmup 10 -r 10 --time-unit=microsecond --export-json benchmarks/multibrot_set/multibrot.exe.json ' ./benchmarks/multibrot_set/multibrot ' RÉSULTAT :
Référence 1 : ./benchmarks/multibrot_set/multibrot
Temps (moyenne ± σ) : 135880,5 µs ± 1175,4 µs [Utilisateur : 133309,3 µs, Système : 1700,1 µs]
Plage (min … max) : 134639,9 µs … 137621,4 µs 10 courses
fn mandelbrot_kernel_SIMD [
simd_width : Int
]( c : ComplexSIMD[float_type, simd_width]) -> SIMD [float_type, simd_width]:
""" A vectorized implementation of the inner mandelbrot computation. """
let cx = c.re
let cy = c.im
var x = SIMD [float_type, simd_width]( 0 )
var y = SIMD [float_type, simd_width]( 0 )
var y2 = SIMD [float_type, simd_width]( 0 )
var iters = SIMD [float_type, simd_width]( 0 )
var t : SIMD [DType.bool, simd_width] = True
for i in range ( MAX_ITERS ):
if not t.reduce_or():
break
y2 = y * y
y = x.fma(y + y, cy)
t = x.fma(x, y2) <= 4
x = x.fma(x, cx - y2)
iters = t.select(iters + 1 , iters)
return iters
fn compute_multibrot_parallelized () -> Tensor[float_type]:
let t = Tensor[float_type](height, width)
@parameter
fn worker ( row : Int):
let scale_x = (max_x - min_x) / width
let scale_y = (max_y - min_y) / height
@parameter
fn compute_vector [ simd_width : Int]( col : Int):
""" Each time we operate on a `simd_width` vector of pixels. """
let cx = min_x + (col + iota[float_type, simd_width]()) * scale_x
let cy = min_y + row * scale_y
let c = ComplexSIMD[float_type, simd_width](cx, cy)
t.data().simd_store[simd_width](
row * width + col, mandelbrot_kernel_SIMD[simd_width](c)
)
# Vectorize the call to compute_vector where call gets a chunk of pixels.
vectorize[simd_width, compute_vector](width)
# Parallelized
parallelize[worker](height, height)
return t
def main ():
_ = compute_multibrot_parallelized()mojo build benchmarks/multibrot_set/multibrot_mojo_parallelize.mojo
hyperfine --warmup 10 -r 10 --time-unit=microsecond --export-json benchmarks/multibrot_set/multibrot_mojo_parallelize.exe.json ' ./benchmarks/multibrot_set/multibrot_mojo_parallelize ' RÉSULTAT :
Référence 1 : ./benchmarks/multibrot_set/multibrot_mojo_parallelize
Temps (moyenne ± σ) : 7 139,4 µs ± 596,4 µs [Utilisateur : 36 535,2 µs, Système : 6 670,1 µs]
Plage (min … max) : 6 222,6 µs … 8 269,7 µs 10 courses
def mandelbrot_kernel(c):
z = c
for i in range(MAX_ITERS):
z = z * z + c # Change this for different Multibrot sets (e.g., 2 for Mandelbrot)
if z.real * z.real + z.imag * z.imag > 4:
return i
return MAX_ITERS
def compute_mandelbrot():
t = [[0 for _ in range(WIDTH)] for _ in range(HEIGHT)] # Pixel matrix
dx = (MAX_X - MIN_X) / WIDTH
dy = (MAX_Y - MIN_Y) / HEIGHT
@par(collapse=2)
for row in range(HEIGHT):
for col in range(WIDTH):
t[row][col] = mandelbrot_kernel(complex(MIN_X + col * dx, MIN_Y + row * dy))
return t
compute_mandelbrot()
Pour un test ou un tracé (décommentez le code dans le fichier)
CODON_PYTHON=/opt/homebrew/opt/[email protected]/Frameworks/Python.framework/Versions/3.11/lib/libpython3.11.dylib codon run --release benchmarks/multibrot_set/multibrot.codonConstruire et exécuter
codon build --release -exe benchmarks/multibrot_set/multibrot.codon -o benchmarks/multibrot_set/multibrot_codon
hyperfine --warmup 10 -r 10 --time-unit=microsecond --export-json benchmarks/multibrot_set/multibrot_codon.json ' ./benchmarks/multibrot_set/multibrot_codon ' RÉSULTAT :
Référence 1 : ./benchmarks/multibrot_set/multibrot_codon
Temps (moyenne ± σ) : 44184,7 µs ± 1142,0 µs [Utilisateur : 248773,9 µs, Système : 72935,3 µs]
Plage (min … max): 42963,8 µs … 46456,2 µs 10 courses
codon build --release -exe benchmarks/multibrot_set/multibrot_codon_par.codon -o benchmarks/multibrot_set/multibrot_codon_par
hyperfine --warmup 10 -r 10 --time-unit=microsecond --export-json benchmarks/multibrot_set/multibrot_codon_par.json ' ./benchmarks/multibrot_set/multibrot_codon_par ' # Merge all JSON files into benchmarks.json
python3 benchmarks/hyperfine-scripts/merge_jsons.py benchmarks/multibrot_set/ benchmarks/multibrot_set/benchmarks.json
python3 benchmarks/hyperfine-scripts/plot2.py benchmarks/multibrot_set/benchmarks.json
python3 benchmarks/hyperfine-scripts/plot3.py benchmarks/multibrot_set/benchmarks.json
python3 benchmarks/hyperfine-scripts/advanced_statistics.py benchmarks/multibrot_set/benchmarks.json > benchmarks/multibrot_set/benchmarks.json.md
silicon benchmarks/multibrot_set/benchmarks.json.md -l python -o benchmarks/multibrot_set/benchmarks.json.md.pngStatistiques avancées
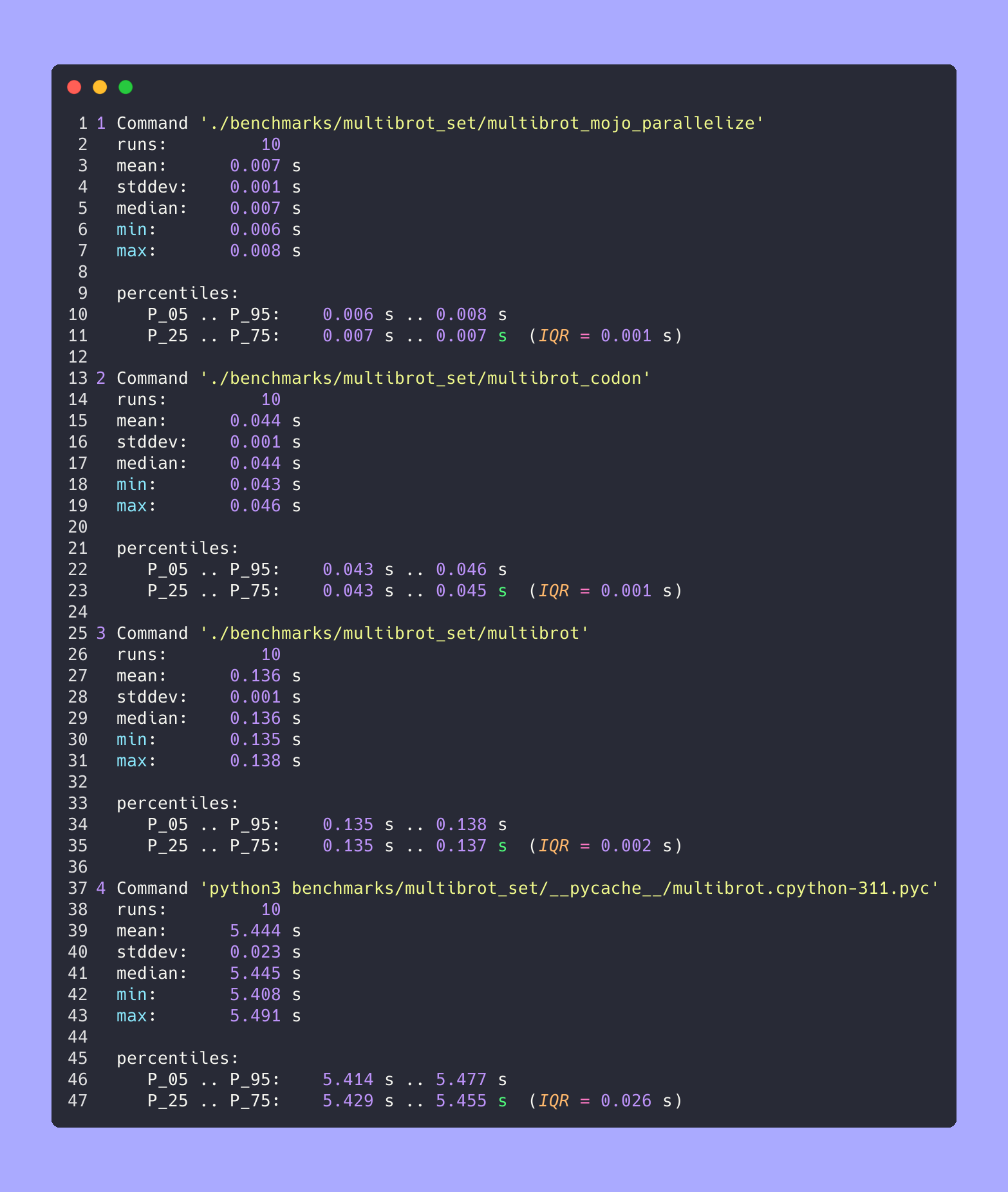
Tous ensemble
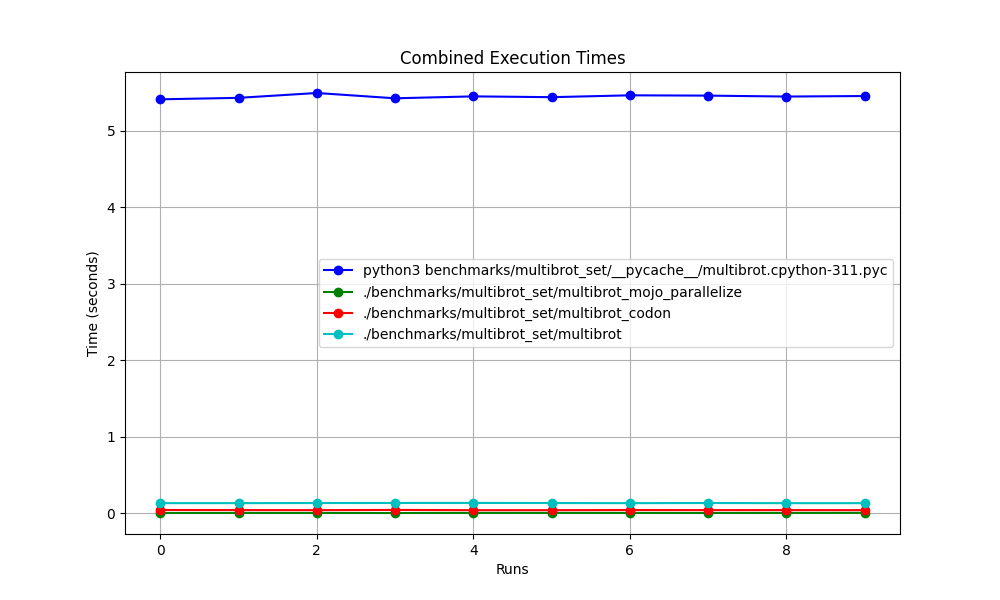
Zoomé
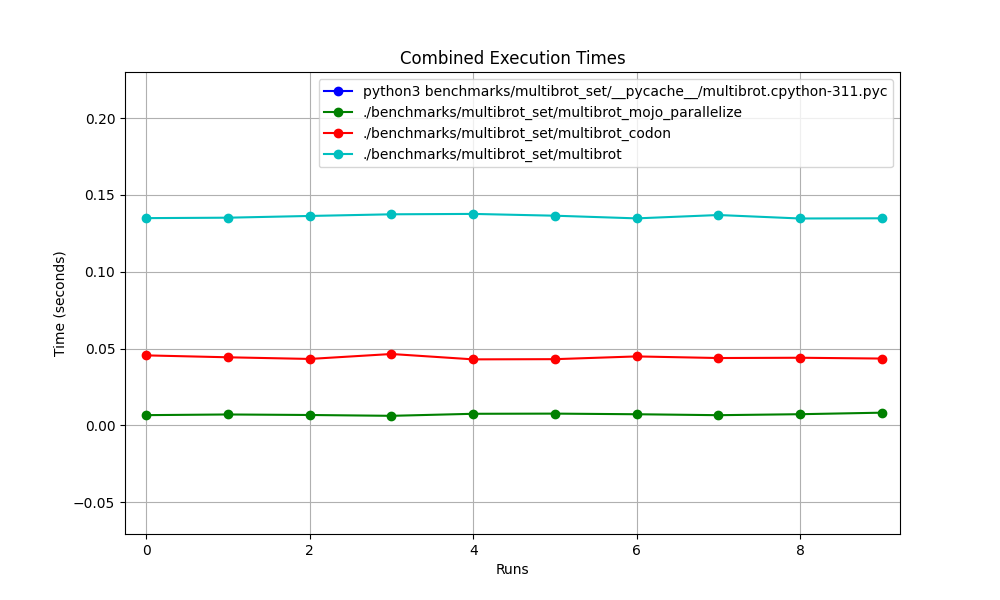
Détaillé un par un
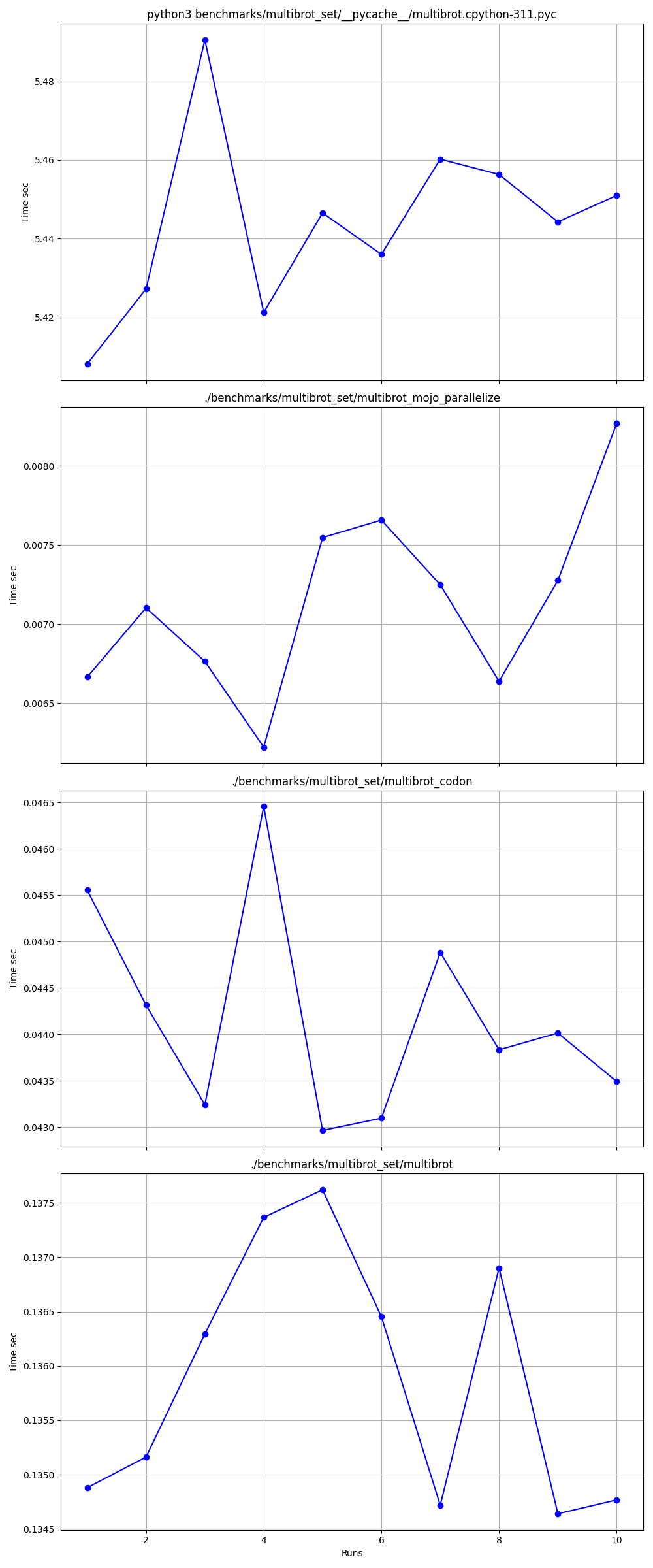
Lieux
Links:
Mandelbrot = Multibrot avec power = 2
z = z ** power + c # You can change this for different setOreiller intégré ImagingEffectMandelbrot
Version Exaloop Codon de Mandelbrot
Version Mojo modulaire de Mandelbrot
Complexe Mojo squared_norm
Matplotlib Mandelbrot
En informatique, l'algorithme de recherche binaire, également connu sous le nom de recherche à demi-intervalle, de recherche logarithmique ou de hachage binaire, est un algorithme de recherche qui trouve la position d'une valeur cible dans un tableau trié.
Faisons du code avec Python, Mojo, Swift, V, Julia, Nim, Zig.
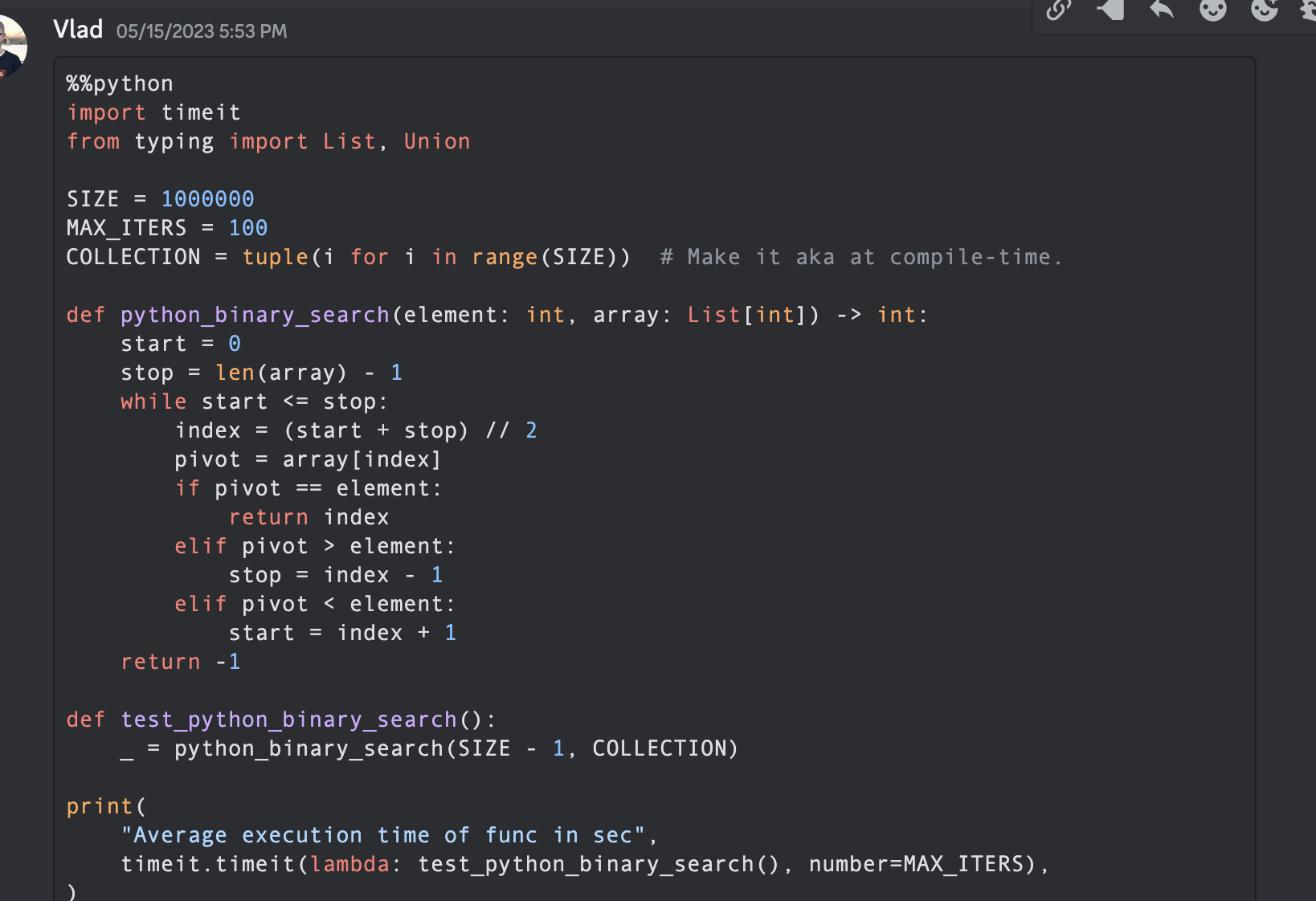
Remarque : Pour les versions Python et Mojo , je laisse une certaine optimisation et je rends le code similaire pour la mesure et la comparaison.
from typing import List
import timeit
SIZE = 1000000
MAX_ITERS = 100
COLLECTION = tuple ( i for i in range ( SIZE )) # Make it aka at compile-time.
def python_binary_search ( element : int , array : List [ int ]) -> int :
start = 0
stop = len ( array ) - 1
while start <= stop :
index = ( start + stop ) // 2
pivot = array [ index ]
if pivot == element :
return index
elif pivot > element :
stop = index - 1
elif pivot < element :
start = index + 1
return - 1
def test_python_binary_search ():
_ = python_binary_search ( SIZE - 1 , COLLECTION )
print (
"Average execution time of func in sec" ,
timeit . timeit ( lambda : test_python_binary_search (), number = MAX_ITERS ),
) """Implements basic binary search."""
from Benchmark import Benchmark
from Vector import DynamicVector
alias SIZE = 1000000
alias NUM_WARMUP = 0
alias MAX_ITERS = 100
fn mojo_binary_search ( element : Int , array : DynamicVector [ Int ]) - > Int :
var start = 0
var stop = len ( array ) - 1
while start <= stop :
let index = ( start + stop ) // 2
let pivot = array [ index ]
if pivot == element :
return index
elif pivot > element :
stop = index - 1
elif pivot < element :
start = index + 1
return - 1
@ parameter # statement runs at compile-time.
fn get_collection () - > DynamicVector [ Int ]:
var v = DynamicVector [ Int ]( SIZE )
for i in range ( SIZE ):
v . push_back ( i )
return v
fn test_mojo_binary_search () - > F64 :
fn test_closure ():
_ = mojo_binary_search ( SIZE - 1 , get_collection ())
return F64 ( Benchmark ( NUM_WARMUP , MAX_ITERS ). run [ test_closure ]()) / 1e9
print (
"Average execution time of func in sec " ,
test_mojo_binary_search (),
)Il s'agit de la première recherche binaire écrite dans la communauté Mojoby (@ego) et publiée dans mojo-chat.
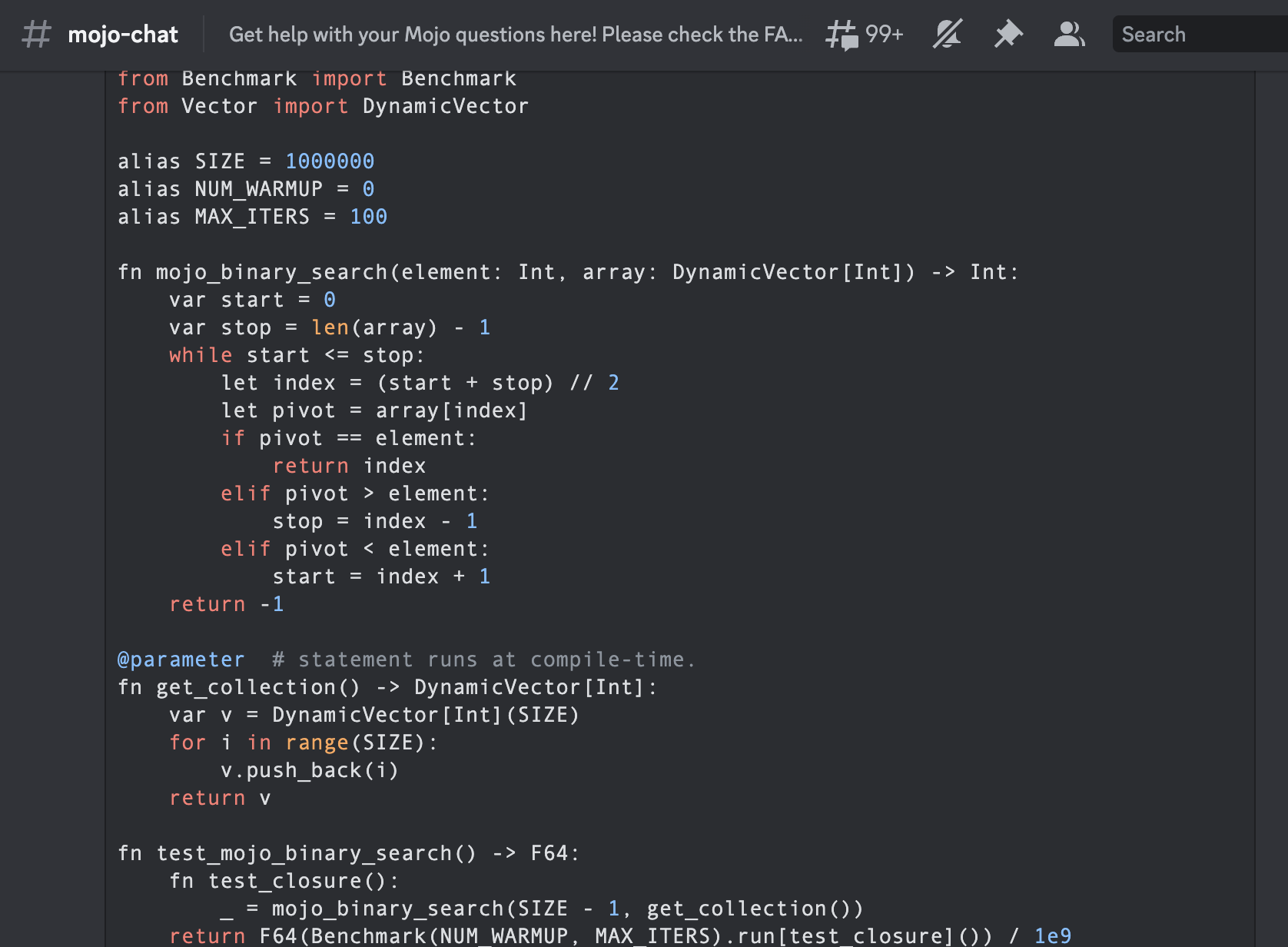
func binarySearch ( items : [ Int ] , elem : Int ) -> Int {
var low = 0
var high = items . count - 1
var mid = 0
while low <= high {
mid = Int ( ( high + low ) / 2 )
if items [ mid ] < elem {
low = mid + 1
} else if items [ mid ] > elem {
high = mid - 1
} else {
return mid
}
}
return - 1
}
let items = [ 1 , 2 , 3 , 4 , 0 ] . sorted ( )
let res = binarySearch ( items : items , elem : 4 )
print ( res ) function binarysearch (lst :: Vector{T} , val :: T ) where T
low = 1
high = length (lst)
while low ≤ high
mid = (low + high) ÷ 2
if lst[mid] > val
high = mid - 1
elseif lst[mid] < val
low = mid + 1
else
return mid
end
end
return 0
end proc binarySearch [T](a: openArray [T], key: T): int =
var b = len (a)
while result < b:
var mid = ( result + b) div 2
if a[mid] < key: result = mid + 1
else : b = mid
if result >= len (a) or a[ result ] != key: result = - 1
let res = @ [ 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 14 , 16 , 18 , 20 , 22 , 25 , 27 , 30 ]
echo binarySearch (res, 10 ) const std = @import ( "std" );
fn binarySearch ( comptime T : type , arr : [] const T , target : T ) ? usize {
var lo : usize = 0 ;
var hi : usize = arr . len - 1 ;
while ( lo <= hi ) {
var mid : usize = ( lo + hi ) / 2 ;
if ( arr [ mid ] == target ) {
return mid ;
} else if ( arr [ mid ] < target ) {
lo = mid + 1 ;
} else {
hi = mid - 1 ;
}
}
return null ;
} fn binary_search (a [] int , value int ) int {
mut low := 0
mut high := a.len - 1
for low < = high {
mid := (low + high) / 2
if a[mid] > value {
high = mid - 1
} else if a[mid] < value {
low = mid + 1
} else {
return mid
}
}
return - 1
}
fn main () {
search_list := [ 1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 , 10 ]
println ( binary_search (search_list, 9 ))
} fn breadth_first_search_path (graph map [ string ][] string , vertex string , target string ) [] string {
mut path := [] string {}
mut visited := [] string {init: vertex}
mut queue := [][][] string {}
queue << [[vertex], path]
for queue.len > 0 {
mut idx := queue.len - 1
node := queue[idx][ 0 ][ 0 ]
path = queue[idx][ 1 ]
queue. delete (idx)
if node == target {
path << node
return path
}
for child in graph[node] {
mut tmp := path. clone ()
if child ! in visited {
visited << child
tmp << node
queue << [[child], tmp]
}
}
}
return path
}
fn main () {
graph := map {
'A' : [ 'B' , 'C' ]
'B' : [ 'A' , 'D' , 'E' ]
'C' : [ 'A' , 'F' ]
'D' : [ 'B' ]
'E' : [ 'B' , 'F' ]
'F' : [ 'C' , 'E' ]
}
println ( 'Graph: $graph ' )
path := breadth_first_search_path (graph, 'A' , 'F' )
println ( 'The shortest path from node A to node F is: $path ' )
assert path == [ 'A' , 'C' , 'F' ]
} import timeit
SIZE = 100
MAX_ITERS = 100
def _fizz_buzz (): # Make it aka at compile-time.
res = []
for n in range ( 1 , SIZE + 1 ):
if ( n % 3 == 0 ) and ( n % 5 == 0 ):
s = "FizzBuzz"
elif n % 3 == 0 :
s = "Fizz"
elif n % 5 == 0 :
s = "Buzz"
else :
s = str ( n )
res . append ( s )
return res
DATA = _fizz_buzz ()
def fizz_buzz ():
print ( " n " . join ( DATA ))
print (
"Average execution time of Python func in sec" ,
timeit . timeit ( lambda : fizz_buzz (), number = MAX_ITERS ),
)
# Average execution time of Python func in sec 0.005334990004485007 ( import '[java.io OutputStream])
( require '[clojure.java.io :as io])
( def devnull ( io/writer ( OutputStream/nullOutputStream )))
( defmacro timeit [n expr]
`(with-out-str ( time
( dotimes [_# ~( Math/pow 1 n)]
( binding [*out* devnull]
~expr)))))
( defmacro macro-fizz-buzz [n]
`( fn []
( print
~( apply str
( for [i ( range 1 ( inc n))]
( cond
( zero? ( mod i 15 )) " FizzBuzz n "
( zero? ( mod i 5 )) " Buzz n "
( zero? ( mod i 3 )) " Fizz n "
:else ( str i " n " )))))))
( print ( timeit 100 ( macro-fizz-buzz 100 )))
; ; "Elapsed time: 0.175486 msecs"
; ; Average execution time of Clojure func in sec 0.000175486 seconds from String import String
from Benchmark import Benchmark
alias SIZE = 100
alias NUM_WARMUP = 0
alias MAX_ITERS = 100
@ parameter # statement runs at compile-time.
fn _fizz_buzz () - > String :
var res : String = ""
for n in range ( 1 , SIZE + 1 ):
if ( n % 3 == 0 ) and ( n % 5 == 0 ):
res += "FizzBuzz"
elif n % 3 == 0 :
res += "Fizz"
elif n % 5 == 0 :
res += "Buzz"
else :
res += String ( n )
res += " n "
return res
fn fizz_buzz ():
print ( _fizz_buzz ())
fn run_benchmark () - > F64 :
fn _closure ():
_ = fizz_buzz ()
return F64 ( Benchmark ( NUM_WARMUP , MAX_ITERS ). run [ _closure ]()) / 1e9
print (
"Average execution time of func in sec " ,
run_benchmark (),
)
# Average execution time of func in sec 0.000104 C'est le premier buzz Fizz écrit en Mojo par la communauté (@Ego).
Nous utiliserons l'algorithme d'une référence bien connue pour le livre d'algorithmes Introduction aux algorithmes A3.
Sa renommée a conduit à l'usage courant de l'abréviation « CLRS » (Cormen, Leiserson, Rivest, Stein), ou, dans la première édition, « CLR » (Cormen, Leiserson, Rivest).
Chapitre 2 "2.3.1 L'approche diviser pour régner".
% % python
import timeit
MAX_ITERS = 100
def merge ( A , p , q , r ):
n1 = q - p + 1
n2 = r - q
L = [ None ] * n1
R = [ None ] * n2
for i in range ( n1 ):
L [ i ] = A [ p + i ]
for j in range ( n2 ):
R [ j ] = A [ q + 1 + j ]
i = 0
j = 0
k = p
while i < n1 and j < n2 :
if L [ i ] <= R [ j ]:
A [ k ] = L [ i ]
i += 1
else :
A [ k ] = R [ j ]
j += 1
k += 1
while i < n1 :
A [ k ] = L [ i ]
i += 1
k += 1
while j < n2 :
A [ k ] = R [ j ]
j += 1
k += 1
def merge_sort ( A , p , r ):
if p < r :
q = ( p + r ) // 2
merge_sort ( A , p , q )
merge_sort ( A , q + 1 , r )
merge ( A , p , q , r )
def run_benchmark_merge_sort ():
A = [ 14 , 72 , 50 , 83 , 18 , 20 , 13 , 30 , 17 , 87 , 94 , 65 , 24 , 99 , 70 , 44 , 5 , 12 , 74 , 6 , 32 , 63 , 91 , 88 , 43 , 54 , 27 , 39 , 64 , 78 , 29 , 62 , 58 , 59 , 61 , 89 , 2 , 15 , 41 , 9 , 93 , 90 , 23 , 96 , 73 , 14 , 8 , 28 , 11 , 42 , 77 , 34 , 52 , 80 , 57 , 84 , 21 , 60 , 66 , 40 , 7 , 85 , 47 , 98 , 97 , 35 , 82 , 36 , 49 , 3 , 68 , 22 , 67 , 81 , 56 , 71 , 4 , 38 , 69 , 95 , 16 , 48 , 1 , 31 , 75 , 19 , 10 , 25 , 79 , 45 , 76 , 33 , 53 , 55 , 46 , 37 , 26 , 51 , 92 , 86 ]
merge_sort ( A , 0 , len ( A ) - 1 )
print (
"Average execution time of Python `merge_sort` in sec" ,
timeit . timeit ( lambda : run_benchmark_merge_sort (), number = MAX_ITERS ),
)
# Average execution time of Python `merge_sort` in sec 0.019136679999064654
def run_benchmark_sort ():
A = [ 14 , 72 , 50 , 83 , 18 , 20 , 13 , 30 , 17 , 87 , 94 , 65 , 24 , 99 , 70 , 44 , 5 , 12 , 74 , 6 , 32 , 63 , 91 , 88 , 43 , 54 , 27 , 39 , 64 , 78 , 29 , 62 , 58 , 59 , 61 , 89 , 2 , 15 , 41 , 9 , 93 , 90 , 23 , 96 , 73 , 14 , 8 , 28 , 11 , 42 , 77 , 34 , 52 , 80 , 57 , 84 , 21 , 60 , 66 , 40 , 7 , 85 , 47 , 98 , 97 , 35 , 82 , 36 , 49 , 3 , 68 , 22 , 67 , 81 , 56 , 71 , 4 , 38 , 69 , 95 , 16 , 48 , 1 , 31 , 75 , 19 , 10 , 25 , 79 , 45 , 76 , 33 , 53 , 55 , 46 , 37 , 26 , 51 , 92 , 86 ]
A . sort ()
print (
"Average execution time of Python builtin `sort` in sec" ,
timeit . timeit ( lambda : run_benchmark_sort (), number = MAX_ITERS ),
)
# Average execution time of Python builtin `sort` in sec 0.00019922800129279494 from Benchmark import Benchmark
from Vector import DynamicVector
from StaticTuple import StaticTuple
from Sort import sort
alias NUM_WARMUP = 0
alias MAX_ITERS = 100
fn merge ( inout A : DynamicVector [ Int ], p : Int , q : Int , r : Int ):
let n1 = q - p + 1
let n2 = r - q
var L = DynamicVector [ Int ]( n1 )
var R = DynamicVector [ Int ]( n2 )
for i in range ( n1 ):
L [ i ] = A [ p + i ]
for j in range ( n2 ):
R [ j ] = A [ q + 1 + j ]
var i = 0
var j = 0
var k = p
while i < n1 and j < n2 :
if L [ i ] <= R [ j ]:
A [ k ] = L [ i ]
i += 1
else :
A [ k ] = R [ j ]
j += 1
k += 1
while i < n1 :
A [ k ] = L [ i ]
i += 1
k += 1
while j < n2 :
A [ k ] = R [ j ]
j += 1
k += 1
fn merge_sort ( inout A : DynamicVector [ Int ], p : Int , r : Int ):
if p < r :
let q = ( p + r ) // 2
merge_sort ( A , p , q )
merge_sort ( A , q + 1 , r )
merge ( A , p , q , r )
@ parameter
fn create_vertor () - > DynamicVector [ Int ]:
let st = StaticTuple [ MAX_ITERS , Int ]( 14 , 72 , 50 , 83 , 18 , 20 , 13 , 30 , 17 , 87 , 94 , 65 , 24 , 99 , 70 , 44 , 5 , 12 , 74 , 6 , 32 , 63 , 91 , 88 , 43 , 54 , 27 , 39 , 64 , 78 , 29 , 62 , 58 , 59 , 61 , 89 , 2 , 15 , 41 , 9 , 93 , 90 , 23 , 96 , 73 , 14 , 8 , 28 , 11 , 42 , 77 , 34 , 52 , 80 , 57 , 84 , 21 , 60 , 66 , 40 , 7 , 85 , 47 , 98 , 97 , 35 , 82 , 36 , 49 , 3 , 68 , 22 , 67 , 81 , 56 , 71 , 4 , 38 , 69 , 95 , 16 , 48 , 1 , 31 , 75 , 19 , 10 , 25 , 79 , 45 , 76 , 33 , 53 , 55 , 46 , 37 , 26 , 51 , 92 , 86 )
var v = DynamicVector [ Int ]( st . __len__ ())
for i in range ( st . __len__ ()):
v . push_back ( st [ i ])
return v
fn run_benchmark_merge_sort () - > F64 :
fn _closure ():
var A = create_vertor ()
merge_sort ( A , 0 , len ( A ) - 1 )
return F64 ( Benchmark ( NUM_WARMUP , MAX_ITERS ). run [ _closure ]()) / 1e9
print (
"Average execution time of Mojo `merge_sort` in sec " ,
run_benchmark_merge_sort (),
)
# Average execution time of Mojo `merge_sort` in sec 1.1345999999999999e-05
fn run_benchmark_sort () - > F64 :
fn _closure ():
var A = create_vertor ()
sort ( A )
return F64 ( Benchmark ( NUM_WARMUP , MAX_ITERS ). run [ _closure ]()) / 1e9
print (
"Average execution time of Mojo builtin `sort` in sec " ,
run_benchmark_sort (),
)
# Average execution time of Mojo builtin `sort` in sec 2.988e-06Vous pouvez l'utiliser comme :
# Usage: merge_sort
var A = create_vertor ()
merge_sort ( A , 0 , len ( A ) - 1 )
print ( len ( A ))
print ( A [ 0 ], A [ 99 ]) from Sort import sort est un peu plus rapide que notre implémentation, mais nous pouvons l'optimiser en profondeur dans le langage et comme d'habitude avec des algorithmes =) et des paradigmes de programmation.
| Lang | seconde |
|---|---|
| Python fusion_sort | 0,019136679 |
| Tri intégré Python | 0,000199228 |
| Mojo merge_sort | 0,000011346 |
| Tri intégré Mojo | 0,000002988 |
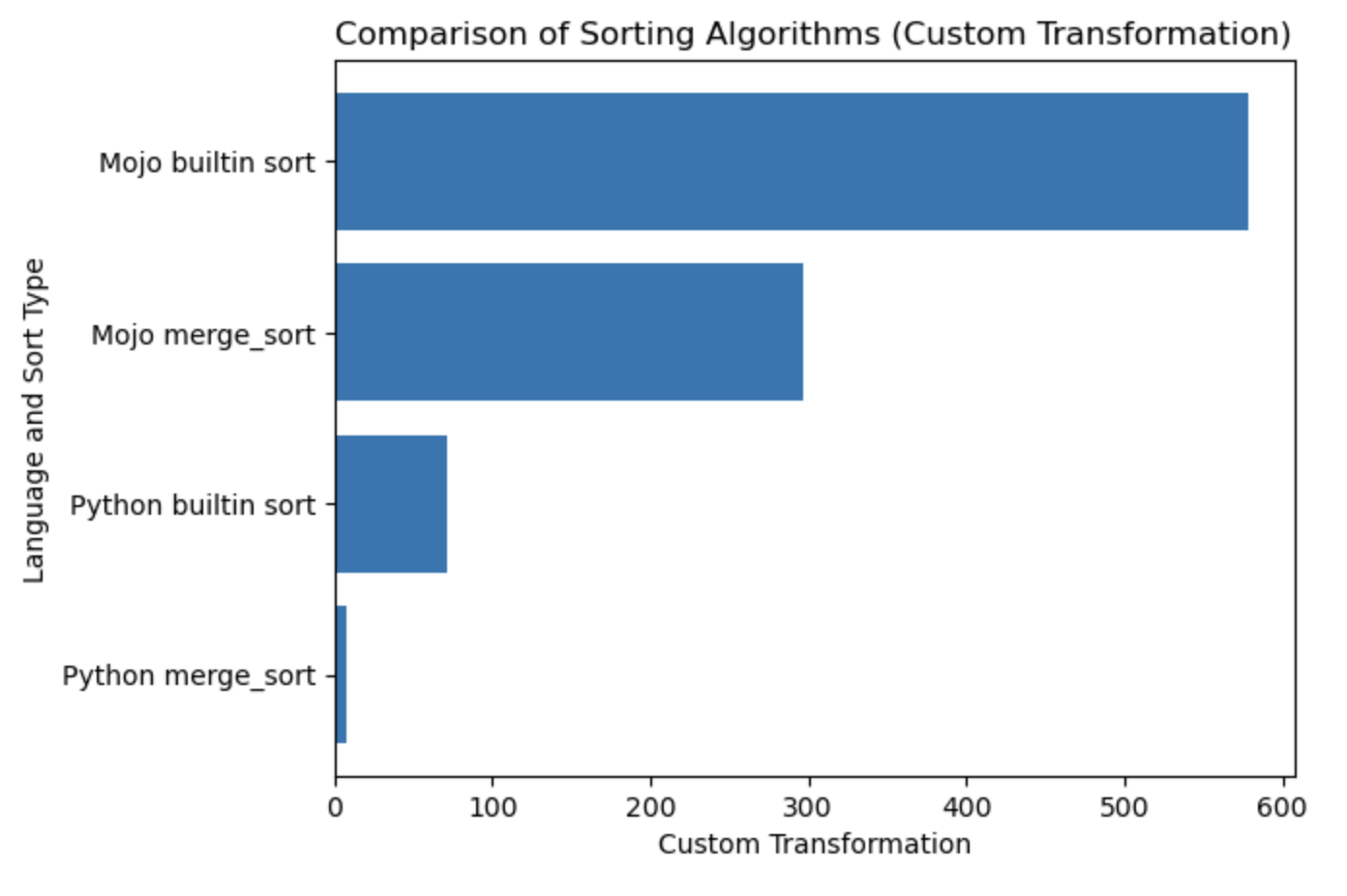
Construisons un tracé pour cette table.
#%%python
import matplotlib . pyplot as plt
import numpy as np
languages = [ 'Python merge_sort' , 'Python builtin sort' , 'Mojo merge_sort' , 'Mojo builtin sort' ]
seconds = [ 0.019136679 , 0.000199228 , 0.000011346 , 0.000002988 ]
# Apply a custom transformation to the values
transformed_seconds = [ np . sqrt ( 1 / x ) for x in seconds ]
plt . barh ( languages , transformed_seconds )
plt . xlabel ( 'Custom Transformation' )
plt . ylabel ( 'Language and Sort Type' )
plt . title ( 'Comparison of Sorting Algorithms (Custom Transformation)' )
plt . show ()Tracez des notes, plus c'est mieux et plus vite.
J'ai fortement recommandé de commencer à partir d'ici HelloMojo et de comprendre le paramétrage des [paramètres] et des [expressions de paramètres] ici. Comme dans cet exemple :
fn concat [ len1 : Int , len2 : Int ]( lhs : MySIMD [ len1 ], rhs : MySIMD [ len2 ]) - > MySIMD [ len1 + len2 ]:
let result = MySIMD [ len1 + len2 ]()
for i in range ( len1 ):
result [ i ] = lhs [ i ]
for j in range ( len2 ):
result [ len1 + j ] = rhs [ j ]
return result
let a = MySIMD [ 2 ]( 1 , 2 )
let x = concat [ 2 , 2 ]( a , a )
x . dump () Heure de compilation [Paramètres] : fn concat[len1: Int, len2: Int] .
Temps d'exécution (Args) : fn concat(lhs: MySIMD, rhs: MySIMD) .
Paramètres Syntaxe PEP695 entre crochets [] .
Maintenant en Python :
def func ( a : _T , b : _T ) -> _T :
...Maintenant dans Mojo :
def func [ T ]( a : T , b : T ) -> T :
... Les [Paramètres] sont nommés et ont des types comme les valeurs normales dans un programme Mojo, mais parameters[] sont évalués au moment de la compilation .
Le programme d'exécution peut utiliser la valeur de [parameters] - car les paramètres sont résolus au moment de la compilation avant d'être nécessaires au programme d'exécution - mais les expressions des paramètres au moment de la compilation ne peuvent pas utiliser de valeurs d'exécution.
Saisie Self à partir du PEP673
fn __sub__ ( self , rhs : Self ) - > Self :
let result = MySIMD [ size ]()
for i in range ( size ):
result [ i ] = self [ i ] - rhs [ i ]
return resultDans la documentation, vous pouvez trouver des champs de mots, c'est-à-dire des attributs de classe dans Python.
Donc, vous les appelez avec dot .
from DType import DType
let bool_type = DType . bool from DType import DType
DType . si8 from DType import DType
from SIMD import SIMD , SI8
alias MY_SIMD_DType_si8 = SIMD [ DType . si8 , 1 ]
alias MY_SI8 = SI8
print ( MY_SIMD_DType_si8 == MY_SI8 )
# true from DType import DType
from SIMD import SIMD , SI8
from Vector import DynamicVector
from String import String
alias a = DynamicVector [ SIMD [ DType . si8 , 1 ]]
alias b = DynamicVector [ SI8 ]
print ( a == b )
print ( a == String )
print ( b == String )
# all true Ainsi, la String n'est qu'un alias pour quelque chose comme DynamicVector[SIMD[DType.si8, 1]] .
VariadicList pour déstructurer/décompresser/accéder aux arguments from List import VariadicList
fn destructuring_arguments ( * args : Int ):
let my_var_list = VariadicList ( args )
for i in range ( len ( my_var_list )):
print ( "argument" , i , ":" , my_var_list [ i ])
destructuring_arguments ( 1 , 2 , 3 , 4 )C’est très utile pour créer des collections initiales. On peut écrire ainsi :
from Vector import DynamicVector
from StaticTuple import StaticTuple
fn create_vertor () - > DynamicVector [ Int ]:
let st = StaticTuple [ 4 , Int ]( 1 , 2 , 3 , 4 )
var v = DynamicVector [ Int ]( st . __len__ ())
for i in range ( st . __len__ ()):
v . push_back ( st [ i ])
return v
v = create_vertor ()
print ( v [ 0 ], v [ 3 ])
# or
from List import VariadicList
fn create_vertor () - > DynamicVector [ Int ]:
let var_list = VariadicList ( 1 , 2 , 3 , 4 )
var v = DynamicVector [ Int ]( len ( var_list ))
for i in range ( len ( var_list )):
v . push_back ( var_list [ i ])
return v
v = create_vertor ()
print ( v [ 0 ], v [ 3 ])En savoir plus sur les fonctions def et fn
from String import String
# String concatenation
print ( String ( "'" ) + String ( 1 ) + "' n " )
# Python's join
print ( String ( "|" ). join ( "a" , "b" , "c" ))
# String format
from IO import _printf as print
let x : Int = 1
print ( "'%i' n " , x . value )Pour une chaîne, vous pouvez utiliser Builtin Slice avec le format de chaîne slice[start:end:step].
from String import String
let hello_mojo = String ( "Hello Mojo!" )
print ( "Till the end:" , hello_mojo [ 0 ::])
print ( "Before last 2 chars:" , hello_mojo [ 0 : - 2 ])
print ( "From start to the end with step 2:" , hello_mojo [ 0 :: 2 ])
print ( "From start to the before last with step 3:" , hello_mojo [ 0 : - 1 : 3 ])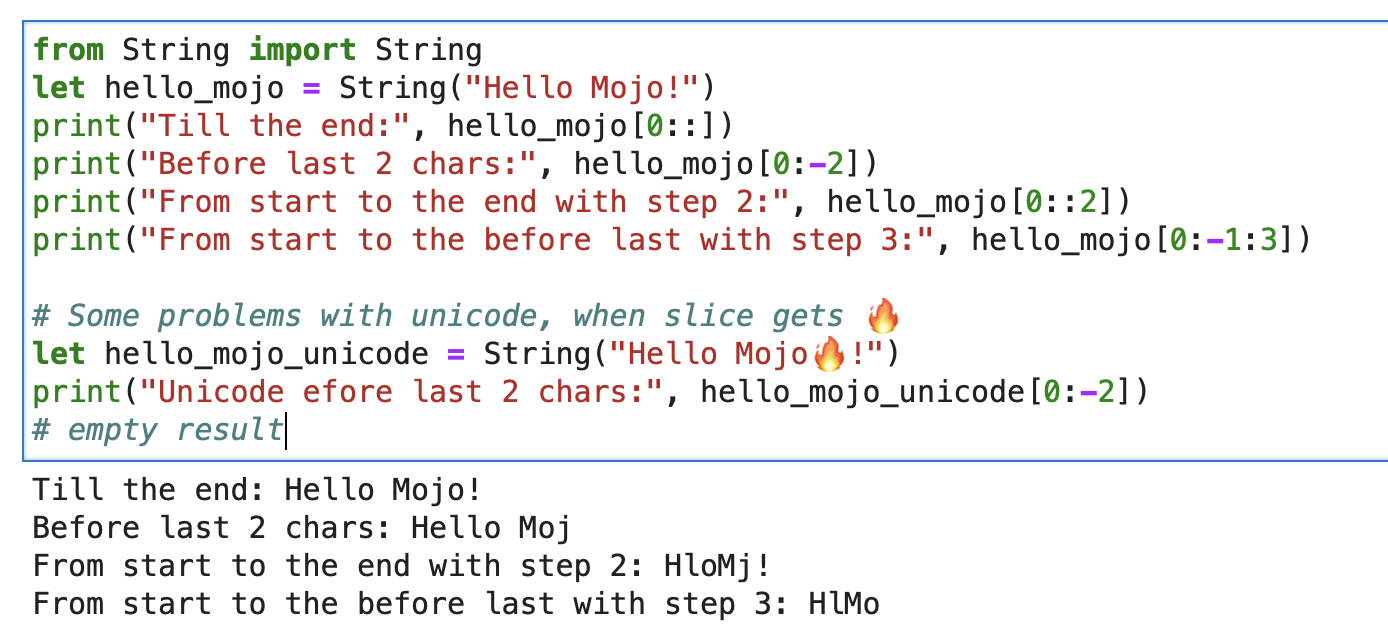
Il y a un problème avec Unicode, lors du découpage :
let hello_mojo_unicode = String ( "Hello Mojo!" )
print ( "Unicode efore last 2 chars:" , hello_mojo_unicode [ 0 : - 2 ])
# no result, silentsVoici une explication et quelques discussions.
mbstowcs - convertit une chaîne multi-octets en chaîne de caractères larges
décorateur struct alias Python @dataclass . Il générera automatiquement les méthodes __init__ , __copyinit__ , __moveinit__ pour vous.
@ value
struct dataclass :
var name : String
var age : Int Notez que le décorateur @value ne fonctionne que sur les types dont les membres sont copyable et/ou movable .
Types triviaux. Ce décorateur indique à Mojo que le type doit être copiable __copyinit__ et mobile __moveinit__ . Il indique également à Mojo de préférer transmettre la valeur dans les registres du CPU. Permet structs d'accepter d'être transmises dans un register au lieu de passer par memory .
@ register_passable ( "trivial" )
struct Int :
var value : __mlir_type . `!pop.scalar<index>`Décorateurs qui offrent un contrôle total sur les optimisations du compilateur . Demande au compilateur de toujours intégrer cette fonction lorsqu'elle est appelée.
@ always_inline
fn foo ( x : Int , y : Int ) - > Int :
return x + y
fn bar ( z : Int ):
let r = foo ( z , z ) # This call will be inlinedIl peut être placé sur des fonctions imbriquées qui capturent les valeurs d'exécution pour créer des fermetures de capture « paramétriques ». Il permet de transmettre les fermetures qui capturent les valeurs d'exécution en tant que valeurs de paramètre.
@ always_inline
@ parameter
fn test (): return Quelques exemples de casting
s : StringLiteral
let p = DTypePointer [ DType . si8 ]( s . data ()). bitcast [ DType . ui8 ]()
var result = 0
result += (( p . simd_load [ 64 ]( offset ) >> 6 ) != 0b10 ). cast [ DType . ui8 ](). reduce_add (). to_int ()
let rest_p : DTypePointer [ DType . ui8 ] = stack_allocation [ simd_width , UI8 , 1 ]()
from Bit import ctlz
s : String
i : Int
let code = s . buffer . data . load ( i )
let byte_length_code = ctlz ( ~ code ). to_int ()DTypePointer - stocke une adresse avec un DType donné, vous permettant d'attribuer, de charger et de modifier des données avec un accès pratique aux opérations SIMD.
from Pointer import DTypePointer
from DType import DType
from Random import rand
from Memory import memset_zero
# `heap`
var my_pointer_on_heap = DTypePointer [ DType . ui8 ]. alloc ( 8 )
memset_zero ( my_pointer_on_heap , 8 )
# `stack or register`
var data = my_pointer_on_heap . simd_load [ 8 ]( 0 )
print ( data )
rand ( my_pointer_on_heap , 4 )
# `data` does not contain a reference to the `heap`, so load the data again
data = my_pointer_on_heap . simd_load [ 8 ]( 0 )
print ( data )
# simd_load and simd_store
var half = my_pointer_on_heap . simd_load [ 4 ]( 0 )
half = half + 1
my_pointer_on_heap . simd_store [ 4 ]( 4 , half )
print ( my_pointer_on_heap . simd_load [ 8 ]( 0 ))
# Pointer move back
my_pointer_on_heap -= 1
print ( my_pointer_on_heap . simd_load [ 8 ]( 0 ))
# Mast free memory
my_pointer_on_heap . free ()Struct peut minimiser le danger potentiel des pointeurs en limitant le détournement.
Excellent article sur le blog Mojo Dojo sur DTypePointer ici
Plus son exemple Matrix Struct et DTypePointer
Le pointeur stocke une adresse sur n’importe quel register_passable type et en alloue un nombre n au heap .
from Pointer import Pointer
from Memory import memset_zero
from String import String
@ register_passable # for syntaxt like `let coord = p1[0]` and let it be passed through registers.
struct Coord : # memory-only type
var x : UI8
var y : UI8
var p1 = Pointer [ Coord ]. alloc ( 2 )
memset_zero ( p1 , 2 )
var coord = p1 [ 0 ] # is an identifier to memory on the stack or in a register
print ( coord . x )
# Store the value
coord . x = 5
coord . y = 5
print ( coord . x )
# We need to store the data.
p1 . store ( 0 , coord )
print ( p1 [ 0 ]. x )
# Mast free memory
p1 . free ()Article complet sur Pointeur
Plus un exemple de pointeur et de structure
Les intrinsèques modulaires sont une sorte de backends d'exécution :
Mojo-> Dialectes MLIR -> backends d'exécution avec code et architectures d'optimisation.
MLIR est une infrastructure de compilateur qui implémente diverses passes de transformation et d'optimisation pour différents langages et architectures de programmation.
MLIR lui-même ne fournit pas directement de fonctionnalités permettant d'interagir avec les appels système du système d'exploitation.
Les interfaces de bas niveau vers les services du système d'exploitation sont généralement gérées au niveau du langage de programmation cible ou du système d'exploitation lui-même. MLIR est conçu pour être indépendant du langage et de la cible, et son objectif principal est de fournir une représentation intermédiaire pour effectuer des optimisations. Pour effectuer des appels système du système d'exploitation dans MLIR, nous devons utiliser un backend spécifique à la cible.
Mais avec ces execution backends , nous avons essentiellement accès aux appels système du système d’exploitation. Et nous avons tout le monde des trucs C/LLVM/Python sous le capot.
Jetons un coup d'œil rapide en pratique :
from OS import getenv
print ( getenv ( "PATH" ))
print ( getenv ( StringRef ( "PATH" )))
# or like this
from SIMD import SI8
from Intrinsics import external_call
var path1 = external_call [ "getenv" , StringRef ]( StringRef ( "PATH" ))
print ( path1 . data )
var path2 = external_call [ "getenv" , StringRef ]( "PATH" )
print ( path2 . data )
let abs_10 = external_call [ "abs" , SI8 , Int ]( - 10 )
print ( abs_10 ) Dans cet exemple simple, nous avons utilisé external_call pour obtenir une variable d'environnement du système d'exploitation avec un type de conversion entre les fonctions Mojo et libc. Plutôt cool, ouais !
J'ai beaucoup d'idées sur ce sujet et j'attends avec impatience l'opportunité de les mettre en œuvre bientôt. Agir peut conduire à des résultats étonnants =)
Faisons quelque chose d'intéressant - appelez libc function gethostname.
La fonction a cette interface int gethostname (char *name, size_t size) .
Pour cela, nous pouvons utiliser la fonction d'assistance external_call du module Intrinsics ou écrire notre propre MLIR.
Allons coder :
from Intrinsics import external_call
from SIMD import SIMD , SI8
from DType import DType
from Vector import DynamicVector
from DType import DType
from Pointer import DTypePointer , Pointer
# We can use `from String import String` but for clarification we will use a full form.
# DynamicVector[SIMD[DType.si8, 1]] == DynamicVector[SI8] == String
# Compile time stuff.
alias cArrayOfStrings = DynamicVector [ SIMD [ DType . si8 , 1 ]]
alias capacity = 1024
var c_pointer_to_array_of_strings = DTypePointer [ DType . si8 ]( cArrayOfStrings ( capacity ). data )
var c_int_result = external_call [ "gethostname" , Int , DTypePointer [ DType . si8 ], Int ]( c_pointer_to_array_of_strings , capacity )
let mojo_string_result = String ( c_pointer_to_array_of_strings . address )
print ( "C function gethostname result code:" , c_int_result )
print ( "C function gethostname result value:" , star_hostname ( mojo_string_result ))
@ always_inline
fn star_hostname ( hostname : String ) - > String :
# [Builtin Slice](https://docs.modular.com/mojo/MojoBuiltin/BuiltinSlice.html)
# string slice[start:end:step]
return hostname [ 0 : - 1 : 2 ]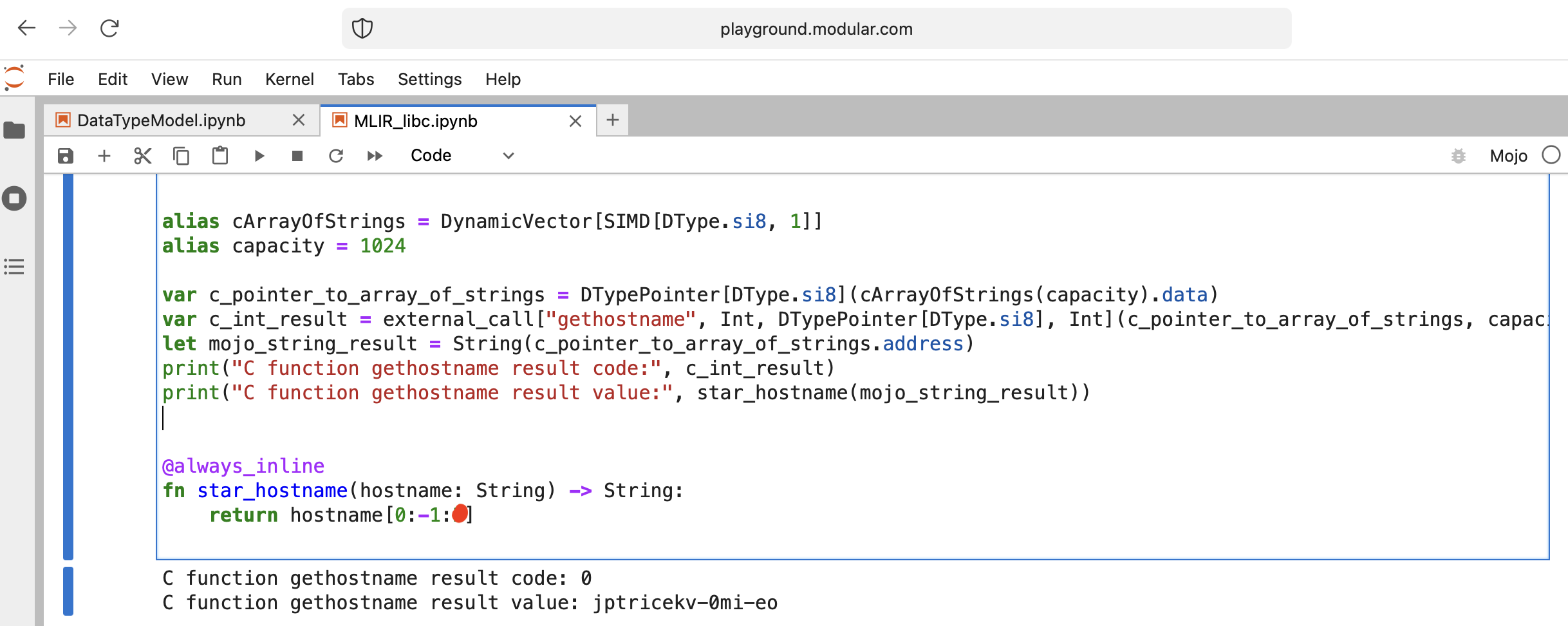
Faisons quelques choses pour un WEB avec Mojo. Nous n'avons pas accès à Internet sur Playground.modular.com. Mais nous pouvons faire des choses intéressantes comme TCP sur une seule machine.
Écrivons le premier code client-serveur TCP dans Mojo avec PythonInterface
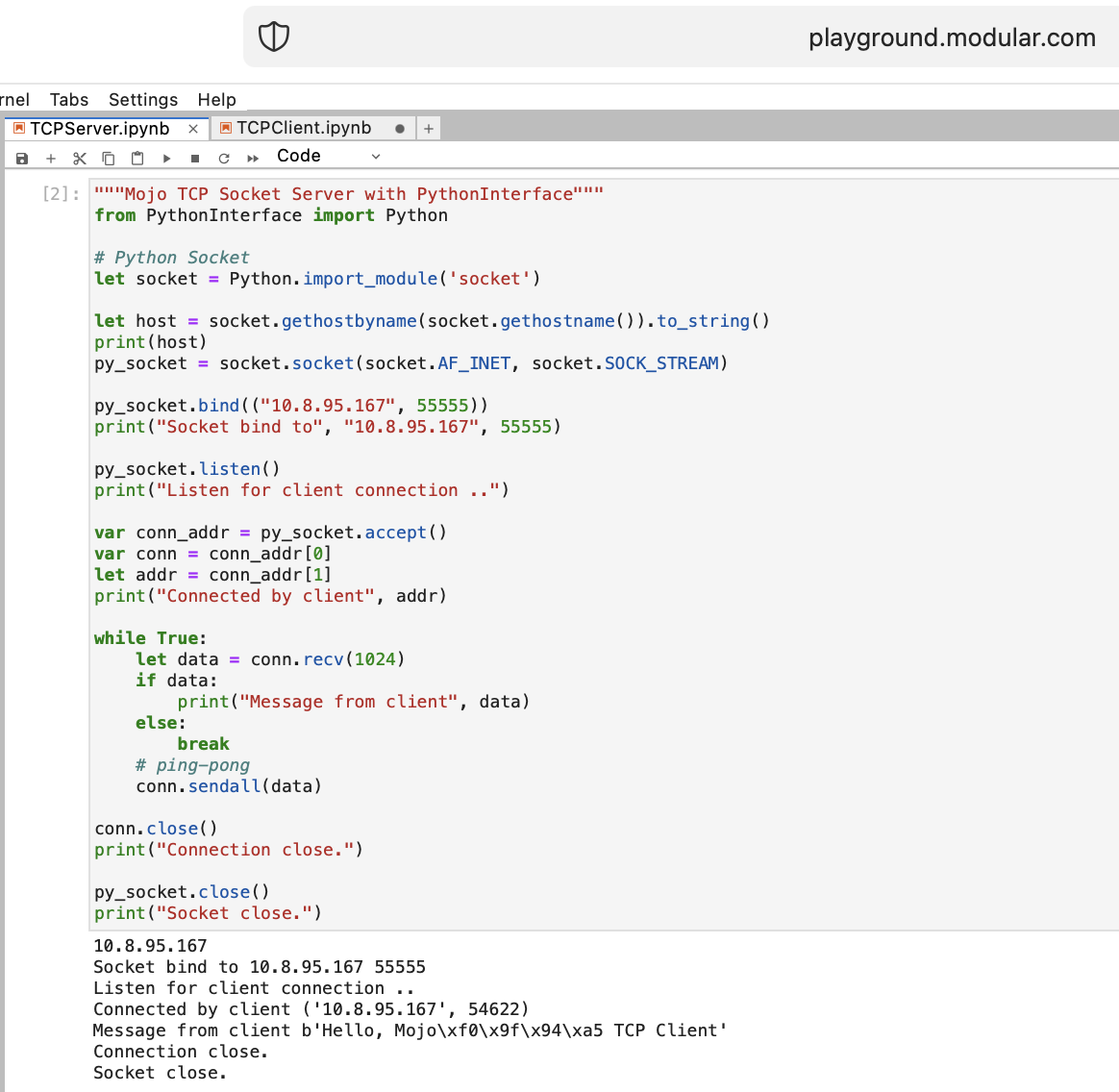
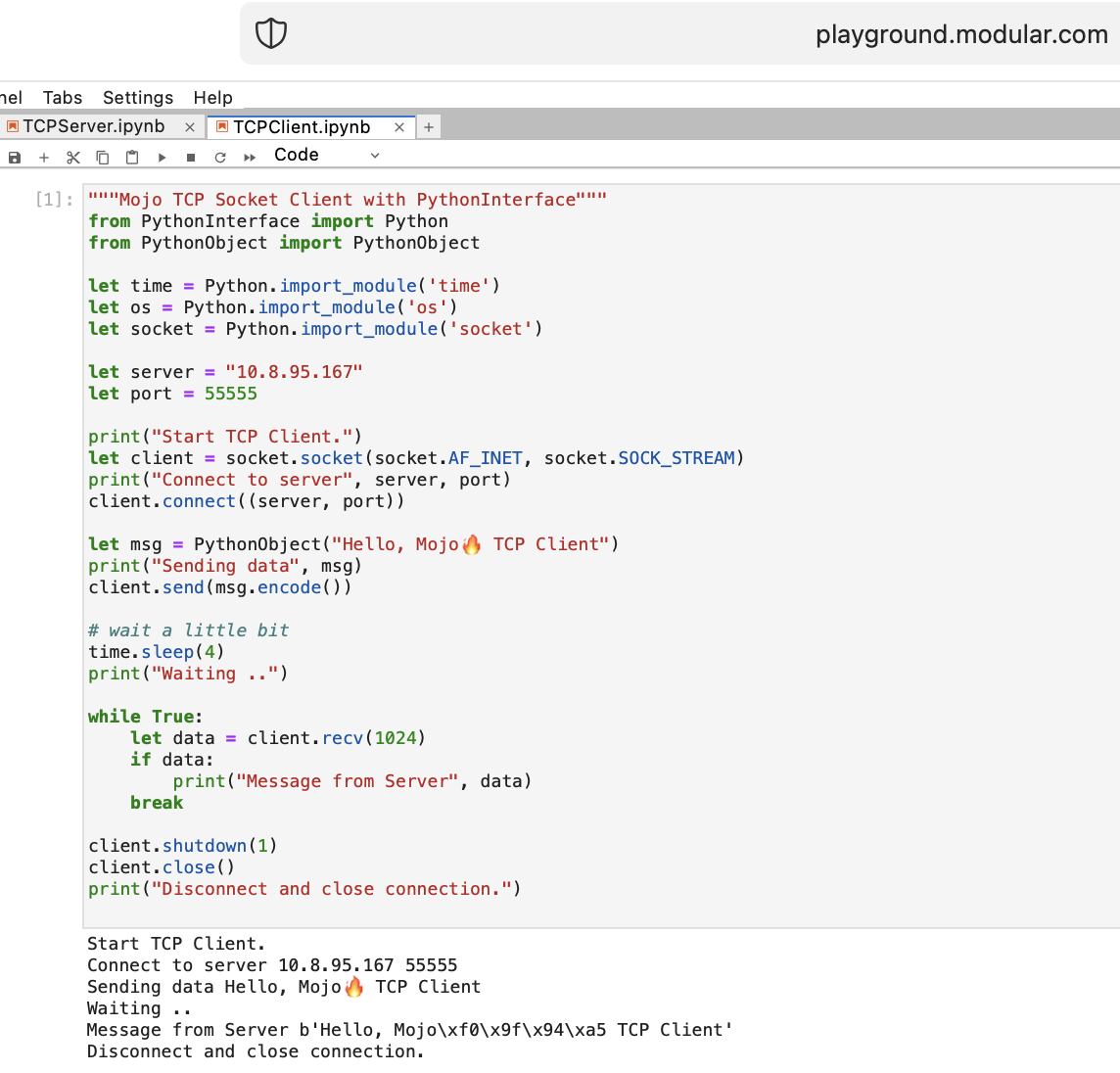
Vous devez créer deux blocs-notes distincts et exécuter d'abord TCPSocketServer , puis TCPSocketClient .
La version Python de ce code est presque la même, sauf :
with la syntaxelet attribuera, b = (1, 2)Après TCP Server dans Mojo, nous allons de l'avant =)
C'est fou, mais essayons d'exécuter le serveur Web Python moderne FastAPI avec Mojo !
Nous devons télécharger le code FastAPI sur le terrain de jeu. Donc, sur votre machine locale, faites
pip install --target=web fastapi uvicorn
tar -czPf web.tar.gz web et téléchargez web.tar.gz sur l'aire de jeux via l'interface Web.
Ensuite, nous devons l' install , il suffit de le placer dans le dossier approprié :
% % python
import os
import site
site_packages_path = site . getsitepackages ()[ 0 ]
# install fastapi
os . system ( f"tar xzf web.tar.gz -C { site_packages_path } " )
os . system ( f"cp -r { site_packages_path } /web/* { site_packages_path } /" )
os . system ( f"ls { site_packages_path } | grep fastapi" )
# clean packages
os . system ( f"rm -rf { site_packages_path } /web" )
os . system ( f"rm web.tar.gz" ) from PythonInterface import Python
# Python fastapi
let fastapi = Python . import_module ( "fastapi" )
let uvicorn = Python . import_module ( "uvicorn" )
var app = fastapi . FastAPI ()
var router = fastapi . APIRouter ()
# tricky part
let py = Python ()
let py_code = """lambda: 'Hello Mojo!'"""
let py_obj = py . evaluate ( py_code )
print ( py_obj )
router . add_api_route ( "/mojo" , py_obj )
app . include_router ( router )
print ( "Start FastAPI WEB Server" )
uvicorn . run ( app )
print ( "Done" ) from PythonInterface import Python
let http_client = Python . import_module ( "http.client" )
let conn = http_client . HTTPConnection ( "localhost" , 8000 )
conn . request ( "GET" , "/mojo" )
let response = conn . getresponse ()
print ( response . status , response . reason , response . read ())Comme d'habitude, vous devez créer deux blocs-notes distincts et exécuter d'abord FastAPI , puis FastAPIClient .
Il y a beaucoup de questions ouvertes, mais dans l’ensemble, nous atteignons l’objectif.
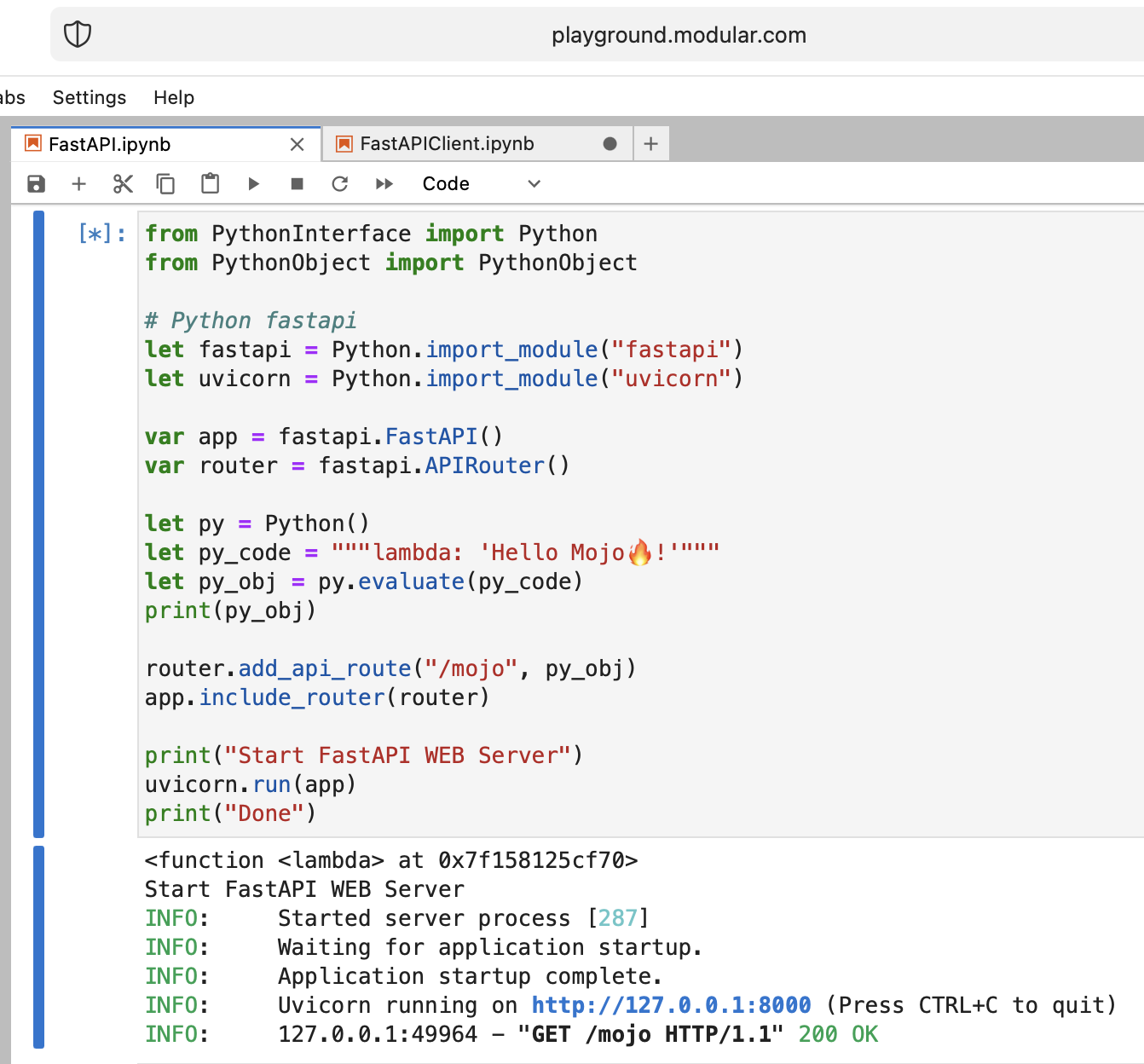
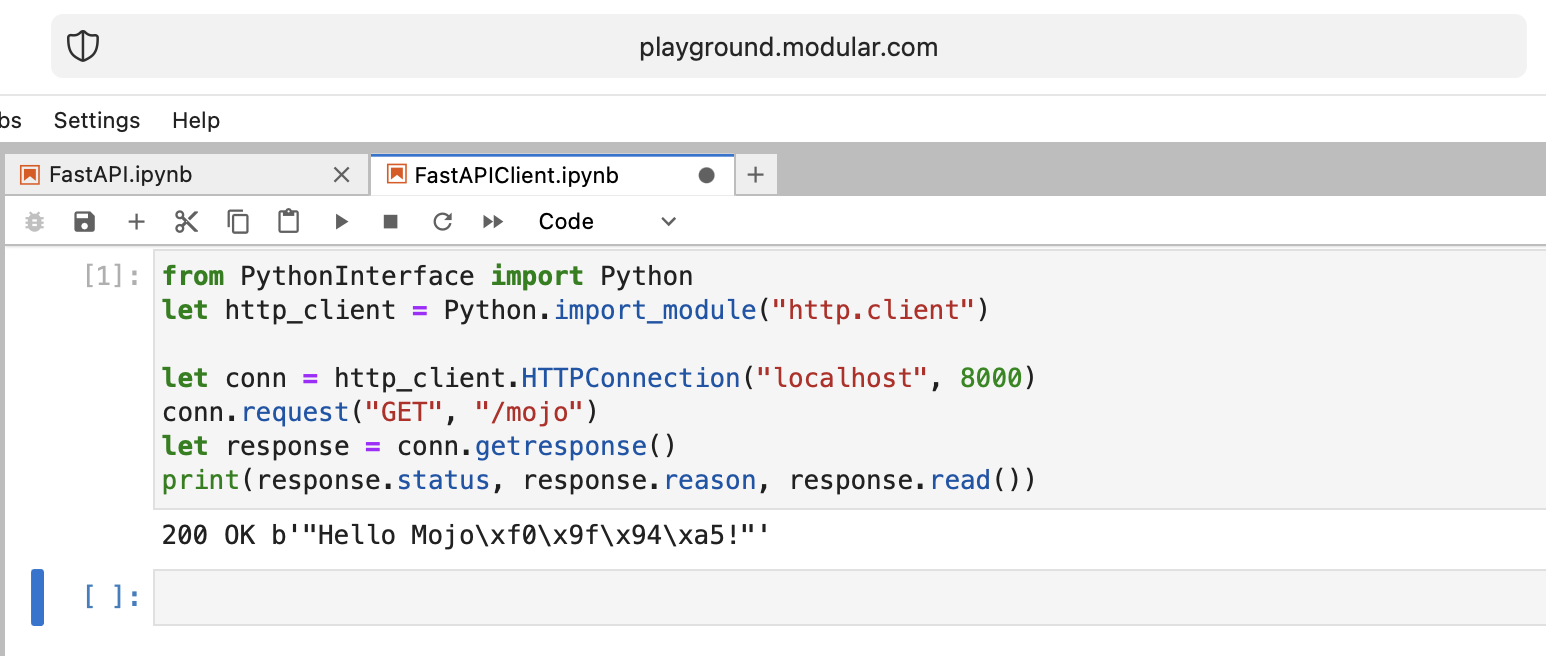
Mojo, bravo !
Quelques questions ouvertes :
from PythonInterface import Python
let pyfn = Python . evaluate ( "lambda x, y: x+y" )
let functools = Python . import_module ( "functools" )
print ( functools . reduce ( pyfn , [ 1 , 2 , 3 , 4 ]))
# How to, without Mojo pyfn.so?
def pyfn ( x , y ):
retyrn x + yL’avenir s’annonce très optimiste !
Links:
Benchmark Mojo vs Numba par Nick Wogan
Utilitaires du temps par Samay Kapadia @Zalando
Connexion à votre terrain de jeu Mojo depuis VSCode ou DataSpell
par Maxim Zaks
from String import String
from PythonInterface import Python
let pathlib = Python . import_module ( 'pathlib' )
let txt = pathlib . Path ( 'nfl.csv' ). read_text ()
let s : String = txt . to_string ()implémentation de la bibliothèque
from DType import DType
from Buffer import Buffer
from Pointer import Pointer
from String import String , chr
let hello = "hello"
let pointer = Pointer ( hello . data ())
print ( "variant 1" )
var result = String ()
for i in range ( len ( hello )):
result += chr ( pointer . bitcast [ Int8 ](). offset ( i ). load (). to_int ())
print ( result )
print ( "variant 2" )
print ( StringRef ( hello . data ()))
print ( "variant 3" )
print ( StringRef ( pointer . address ))
print ( "variant 4" )
let pm : Pointer [ __mlir_type . `!pop.scalar<si8>` ] = Pointer ( hello . data ())
print ( StringRef ( pm . address ))
print ( "variant 5" )
print ( String ( pointer . address ))
print ( "variant 6" )
let x = Buffer [ 8 , DType . int8 ]( pointer )
let array = x . simd_load [ 10 ]( 0 )
var result = String ()
for i in range ( len ( array )):
result += chr ( array [ i ]. to_int ())
print ( result )right click le fichier dans l'explorateur et appuyez sur Open With > Editorselect all et copy.ipynbGithub le restitue correctement, puis si quelqu'un veut essayer le code dans son terrain de jeu, il peut copier-coller le code brut.
C'est mon point de vue personnel, alors ne me jugez pas trop durement.
Je ne peux pas dire que Mojo soit un langage de programmation facile à apprendre, comme Python par exemple.
Cela nécessite beaucoup de compréhension, de patience et d’expérience dans tout autre langage de programmation.
Si vous voulez construire quelque chose de pas anodin, ce sera dur mais drôle !
Cela fait 2 semaines que j'ai entrepris ce voyage et je suis ravi de partager que je connais désormais bien le Mojo.
Les subtilités de sa structure et de sa syntaxe ont commencé à se dévoiler sous mes yeux , et je suis rempli d'une nouvelle compréhension .
Je suis fier de dire que je peux désormais créer du code en toute confiance dans ce langage, ce qui me permet de donner vie à un large éventail d' idées .
Mojo est un langage de programmation de Modular Inc. Pourquoi Mojo dont nous avons discuté ici. À propos de l'entreprise, nous en savons moins, mais elle porte un nom très sympa Modular , auquel on peut faire référence :
"En d'autres termes : Mojo n'est pas magique, c'est modulaire."
Tout sur l'informatique, la programmation, l'IA/ML. Un très bon nom de domaine qui décrit avec précision le sens de la Société.
Il existe des documents supplémentaires sur l'histoire de la marque Modular et sur l'aide à Modular pour humaniser l'IA à travers la marque.
Aujourd'hui, je voudrais raconter une histoire sur le problème de Python Enum. En tant qu'ingénieurs logiciels, nous le rencontrons souvent sur un WEB. Supposons que nous ayons ce schéma de base de données (PostgreSQL) avec enum de statut :
CREATE TYPE public .status_type AS ENUM (
' FIRST ' ,
' SECOND '
);Dans un code Python, nous avons besoin de noms et de valeurs sous forme de chaînes (supposons que nous utilisons GraphQL avec un type ENUM pour notre côté frontend), et nous devons maintenir leur ordre et avoir la possibilité de comparer ces énumérations :
order2.status > order1.status > 'FIRST'
C'est donc un problème pour la plupart des langages courants =) mais nous pouvons utiliser une fonctionnalité Python little-known et remplacer la méthode de classe enum : __new__ .
MALE -> 1 , FEMALE -> 2 , comme le fait PostgreSQL.len ! import enum
from functools import total_ordering
@ total_ordering
@ enum . unique
class BaseUniqueSortedEnum ( enum . Enum ):
"""Base unique enum class with ordering."""
def __new__ ( cls , * args , ** kwargs ):
obj = object . __new__ ( cls )
obj . index = len ( cls . __members__ ) + 1 # This code line is a piece of advice, an insight and a tip!
return obj
# and then boring Python's magic methods as usual...
def __hash__ ( self ) -> int :
return hash (
f" { self . __module__ } _ { self . __class__ . __name__ } _ { self . name } _ { self . value } "
)
def __eq__ ( self , other ) -> bool :
self . _check_type ( other )
return super (). __eq__ ( other )
def __lt__ ( self , other ) -> bool :
self . _check_type ( other )
return self . index < other . index
def _check_type ( self , other ) -> None :
if type ( self ) != type ( other ):
raise TypeError ( f"Different types of Enum: { self } != { other } " )
class Dog ( BaseUniqueSortedEnum ):
# THIS ORDER MATTERS!
BLOODHOUND = "BLOODHOUND"
WEIMARANER = "WEIMARANER"
SAME = "SAME"
class Cat ( BaseUniqueSortedEnum )
# THIS ORDER MATTERS!
BRITISH = "BRITISH"
SCOTTISH = "SCOTTISH"
SAME = "SAME"
# and some tests
assert Dog . BLOODHOUND < Dog . WEIMARANER
assert Dog . BLOODHOUND <= Dog . WEIMARANER
assert Dog . BLOODHOUND != Dog . WEIMARANER
assert Dog . BLOODHOUND == Dog . BLOODHOUND
assert Dog . WEIMARANER == Dog . WEIMARANER
assert Dog . WEIMARANER > Dog . BLOODHOUND
assert Dog . WEIMARANER >= Dog . BLOODHOUND
assert Cat . BRITISH < Cat . SCOTTISH
assert Cat . BRITISH <= Cat . SCOTTISH
assert Cat . BRITISH != Cat . SCOTTISH
assert Cat . BRITISH == Cat . BRITISH
assert Cat . SCOTTISH == Cat . SCOTTISH
assert Cat . SCOTTISH > Cat . BRITISH
assert Cat . SCOTTISH >= Cat . BRITISH
assert hash ( Dog . BLOODHOUND ) == hash ( Dog . BLOODHOUND )
assert hash ( Dog . WEIMARANER ) == hash ( Dog . WEIMARANER )
assert hash ( Dog . BLOODHOUND ) != hash ( Dog . WEIMARANER )
assert hash ( Dog . SAME ) != hash ( Cat . SAME )
# raise TypeError
Dog . SAME <= Cat . SAME
Dog . SAME < Cat . SAME
Dog . SAME > Cat . SAME
Dog . SAME >= Cat . SAME
Dog . SAME != Cat . SAME La fin de l'histoire. et utilisez cet aperçu Python ENUM pour votre codage !