7 fonctions JavaScript simples qui vous donneront une idée de la façon dont les machines peuvent réellement « apprendre ».
Dans d'autres langues : Русский, Português
Cela pourrait également vous intéresser ? Expériences interactives d'apprentissage automatique
NanoNeuron est une version simplifiée du concept Neuron de Neural Networks. NanoNeuron est formé pour convertir les valeurs de température de Celsius en Fahrenheit.
L'exemple de code NanoNeuron.js contient 7 fonctions JavaScript simples (qui touchent à la prédiction de modèle, au calcul des coûts, à la propagation avant/arrière et à la formation) qui vous donneront une idée de la façon dont les machines peuvent réellement « apprendre ». Pas de bibliothèques tierces, pas d'ensembles de données ou de dépendances externes, uniquement des fonctions JavaScript pures et simples.
☝ Ces fonctions ne sont en aucun cas un guide complet de l'apprentissage automatique. De nombreux concepts d’apprentissage automatique sont ignorés et simplifiés à l’excès ! Cette simplification est faite exprès pour donner au lecteur une compréhension et une sensation vraiment basiques de la façon dont les machines peuvent apprendre et, finalement, pour permettre au lecteur de reconnaître qu'il ne s'agit pas de « MAGIE d'apprentissage automatique » mais plutôt de « MATH d'apprentissage automatique » ?.
Vous avez probablement entendu parler des neurones dans le contexte des réseaux de neurones. NanoNeuron est exactement cela, mais plus simple et nous allons l'implémenter à partir de zéro. Pour des raisons de simplicité, nous n'allons même pas construire un réseau sur les NanoNeurons. Nous ferons en sorte que tout fonctionne tout seul, faisant des prédictions magiques pour nous. À savoir, nous apprendrons à ce nanoneurone singulier à convertir (prédire) la température de Celsius en Fahrenheit.
À propos, la formule pour convertir Celsius en Fahrenheit est la suivante :
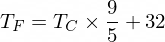
Mais pour l'instant notre NanoNeuron n'en est pas au courant...
Implémentons notre fonction de modèle NanoNeuron. Il implémente une dépendance linéaire de base entre x et y qui ressemble à y = w * x + b . Dire simplement que notre NanoNeuron est un « enfant » dans une « école » à qui on apprend à tracer la ligne droite en coordonnées XY .
Les variables w , b sont des paramètres du modèle. NanoNeuron ne connaît que ces deux paramètres de la fonction linéaire. Ces paramètres sont quelque chose que NanoNeuron va « apprendre » au cours du processus de formation.
La seule chose que NanoNeuron peut faire est d'imiter la dépendance linéaire. Dans sa méthode predict() il accepte certaines entrées x et prédit la sortie y . Pas de magie ici.
function NanoNeuron ( w , b ) {
this . w = w ;
this . b = b ;
this . predict = ( x ) => {
return x * this . w + this . b ;
}
}(...attendez... la régression linéaire, c'est vous ?) ?
La valeur de température en Celsius peut être convertie en Fahrenheit à l'aide de la formule suivante : f = 1.8 * c + 32 , où c est une température en Celsius et f est la température calculée en Fahrenheit.
function celsiusToFahrenheit ( c ) {
const w = 1.8 ;
const b = 32 ;
const f = c * w + b ;
return f ;
} ; A terme nous voulons apprendre à notre NanoNeuron à imiter cette fonction (pour apprendre que w = 1.8 et b = 32 ) sans connaître ces paramètres à l'avance.
Voici à quoi ressemble la fonction de conversion Celsius en Fahrenheit :
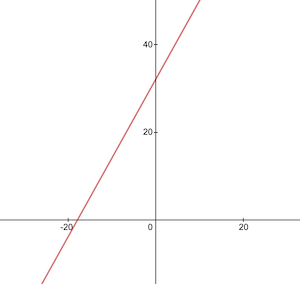
Avant la formation, nous devons générer des ensembles de données de formation et de test basés sur la fonction celsiusToFahrenheit() . Les ensembles de données sont constitués de paires de valeurs d'entrée et de valeurs de sortie correctement étiquetées.
Dans la vraie vie, dans la plupart des cas, ces données seraient collectées plutôt que générées. Par exemple, nous pourrions avoir un ensemble d’images de nombres dessinés à la main et l’ensemble de nombres correspondant qui explique quel nombre est écrit sur chaque image.
Nous utiliserons des exemples de données de TRAINING pour entraîner notre NanoNeuron. Avant que notre NanoNeuron grandisse et soit capable de prendre des décisions par lui-même, nous devons lui apprendre ce qui est bien et ce qui ne va pas à l'aide d'exemples de formation.
Nous utiliserons des exemples de TEST pour évaluer les performances de notre NanoNeuron sur les données qu'il n'a pas vues pendant la formation. C’est à ce moment-là que nous pouvons voir que notre « enfant » a grandi et peut prendre des décisions par lui-même.
function generateDataSets ( ) {
// xTrain -> [0, 1, 2, ...],
// yTrain -> [32, 33.8, 35.6, ...]
const xTrain = [ ] ;
const yTrain = [ ] ;
for ( let x = 0 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTrain . push ( x ) ;
yTrain . push ( y ) ;
}
// xTest -> [0.5, 1.5, 2.5, ...]
// yTest -> [32.9, 34.7, 36.5, ...]
const xTest = [ ] ;
const yTest = [ ] ;
// By starting from 0.5 and using the same step of 1 as we have used for training set
// we make sure that test set has different data comparing to training set.
for ( let x = 0.5 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTest . push ( x ) ;
yTest . push ( y ) ;
}
return [ xTrain , yTrain , xTest , yTest ] ;
} Nous avons besoin d'une métrique qui nous montrera à quel point la prédiction de notre modèle est proche des valeurs correctes. Le calcul du coût (l'erreur) entre la valeur de sortie correcte de y et prediction créée par notre NanoNeuron sera effectué à l'aide de la formule suivante :
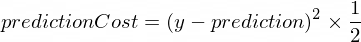
Il s’agit d’une simple différence entre deux valeurs. Plus les valeurs sont proches les unes des autres, plus la différence est faible. Nous utilisons ici une puissance de 2 juste pour nous débarrasser des nombres négatifs afin que (1 - 2) ^ 2 soit identique à (2 - 1) ^ 2 . La division par 2 a lieu juste pour simplifier davantage la formule de propagation vers l'arrière (voir ci-dessous).
La fonction de coût dans ce cas sera aussi simple que :
function predictionCost ( y , prediction ) {
return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
} Faire une propagation vers l'avant signifie faire une prédiction pour tous les exemples de formation à partir des ensembles de données xTrain et yTrain et calculer le coût moyen de ces prédictions en cours de route.
Nous laissons simplement notre NanoNeuron exprimer son opinion, à ce stade, en lui permettant simplement de deviner comment convertir la température. C'est peut-être bêtement faux ici. Le coût moyen nous montrera à quel point notre modèle est erroné à l’heure actuelle. Cette valeur de coût est vraiment importante depuis la modification des paramètres du NanoNeuron w et b , et en refaisant la propagation vers l'avant ; nous pourrons évaluer si notre NanoNeuron est devenu plus intelligent ou non après le changement de ces paramètres.
Le coût moyen sera calculé selon la formule suivante :
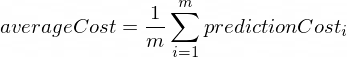
Où m est un nombre d'exemples de formation (dans notre cas : 100 ).
Voici comment nous pouvons l'implémenter dans le code :
function forwardPropagation ( model , xTrain , yTrain ) {
const m = xTrain . length ;
const predictions = [ ] ;
let cost = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
cost += predictionCost ( yTrain [ i ] , prediction ) ;
predictions . push ( prediction ) ;
}
// We are interested in average cost.
cost /= m ;
return [ predictions , cost ] ;
}Lorsque nous savons à quel point les prédictions de notre NanoNeuron sont bonnes ou fausses (basées sur le coût moyen à ce stade), que devons-nous faire pour rendre les prédictions plus précises ?
La propagation vers l'arrière nous donne la réponse à cette question. La propagation vers l'arrière est le processus d'évaluation du coût de la prédiction et d'ajustement des paramètres w et b du NanoNeuron afin que les prédictions suivantes et futures soient plus précises.
C'est ici que l'apprentissage automatique ressemble à de la magie ?♂️. Le concept clé ici est la dérivée qui montre la mesure à prendre pour se rapprocher du minimum de la fonction de coût.
N'oubliez pas que trouver le minimum d'une fonction de coût est le but ultime du processus de formation. Si nous trouvons des valeurs pour w et b telles que notre fonction de coût moyen soit petite, cela signifierait que le modèle NanoNeuron fait des prédictions vraiment bonnes et précises.
Les produits dérivés constituent un sujet important et distinct que nous n’aborderons pas dans cet article. MathIsFun est une bonne ressource pour en avoir une compréhension de base.
Une chose à propos des dérivées qui vous aidera à comprendre le fonctionnement de la propagation vers l'arrière est que la dérivée, de par sa signification, est une ligne tangente à la courbe de fonction qui pointe vers la direction du minimum de la fonction.
Source de l'image : MathIsFun
Par exemple, sur le graphique ci-dessus, vous pouvez voir que si nous sommes au point (x=2, y=4) alors la pente nous dit d'aller left et down pour arriver au minimum de la fonction. Notez également que plus la pente est grande, plus vite nous devons nous déplacer vers le minimum.
Les dérivées de notre fonction averageCost pour les paramètres w et b ressemblent à ceci :
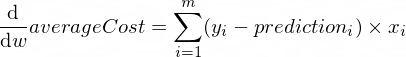
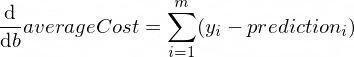
Où m est un nombre d'exemples de formation (dans notre cas : 100 ).
Vous pouvez en savoir plus sur les règles de dérivée et comment obtenir une dérivée de fonctions complexes ici.
function backwardPropagation ( predictions , xTrain , yTrain ) {
const m = xTrain . length ;
// At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
// Therefore we're setting up the changing steps for each parameters to 0.
let dW = 0 ;
let dB = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
dB += yTrain [ i ] - predictions [ i ] ;
}
// We're interested in average deltas for each params.
dW /= m ;
dB /= m ;
return [ dW , dB ] ;
} Nous savons maintenant comment évaluer l'exactitude de notre modèle pour tous les exemples d'ensembles de formation ( propagation vers l'avant ). Nous savons également faire de petits ajustements aux paramètres w et b de notre modèle NanoNeuron ( propagation vers l'arrière ). Mais le problème est que si nous effectuons une propagation vers l'avant puis vers l'arrière une seule fois, il ne suffira pas à notre modèle d'apprendre les lois/tendances des données d'entraînement. Vous pouvez comparer cela à la fréquentation d’une journée d’école primaire pour l’enfant. Il/elle ne devrait pas aller à l’école une fois, mais jour après jour et année après année pour apprendre quelque chose.
Nous devons donc répéter plusieurs fois la propagation avant et arrière de notre modèle. C'est exactement ce que fait la fonction trainModel() . C'est comme un "professeur" pour notre modèle NanoNeuron :
epochs ) avec notre modèle NanoNeuron un peu stupide et essaiera de le former/enseigner,xTrain et yTrain ) pour la formation,alpha Quelques mots sur le taux d'apprentissage alpha . Il s'agit simplement d'un multiplicateur pour les valeurs dW et dB que nous avons calculées lors de la propagation vers l'arrière. Ainsi, la dérivée nous a indiqué la direction que nous devons prendre pour trouver un minimum de la fonction de coût (signe dW et dB ) et elle nous a également montré à quelle vitesse nous devons aller dans cette direction (valeurs absolues de dW et dB ). Nous devons maintenant multiplier ces tailles de pas en alpha juste pour ajuster notre mouvement au minimum plus rapidement ou plus lentement. Parfois, si nous utilisons de grandes valeurs pour alpha , nous pouvons simplement sauter par-dessus le minimum et ne jamais le trouver.
L'analogie avec l'enseignant serait que plus il pousse fort notre « nano-enfant », plus notre « nano-enfant » apprendra vite, mais si l'enseignant pousse trop fort, le « enfant » fera une dépression nerveuse et gagnera. Je ne peux rien apprendre ?.
Voici comment nous allons mettre à jour les paramètres w et b de notre modèle :
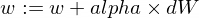
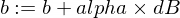
Et voici notre fonction formateur :
function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
// The is the history array of how NanoNeuron learns.
const costHistory = [ ] ;
// Let's start counting epochs.
for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
// Forward propagation.
const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
costHistory . push ( cost ) ;
// Backward propagation.
const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
// Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
nanoNeuron . w += alpha * dW ;
nanoNeuron . b += alpha * dB ;
}
return costHistory ;
}Utilisons maintenant les fonctions que nous avons créées ci-dessus.
Créons notre instance de modèle NanoNeuron. Pour le moment, le NanoNeuron ne sait pas quelles valeurs doivent être définies pour les paramètres w et b . Alors configurons w et b au hasard.
const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;Générez des ensembles de données de formation et de test.
const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ; Entraîneons le modèle avec de petites étapes incrémentielles ( 0.0005 ) pendant 70000 époques. Vous pouvez jouer avec ces paramètres, ils sont définis de manière empirique.
const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;Vérifions comment la fonction de coût a évolué au cours de la formation. Nous nous attendons à ce que le coût après la formation soit bien inférieur à celui d'avant. Cela signifierait que NanoNeuron serait devenu plus intelligent. L’inverse est également possible.
console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024 C'est ainsi que le coût de la formation évolue au fil des époques. Sur les axes x se trouve le numéro d’époque x1000.
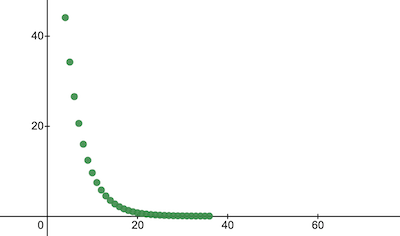
Jetons un coup d'œil aux paramètres du NanoNeuron pour voir ce qu'il a appris. Nous nous attendons à ce que les paramètres w et b du NanoNeuron soient similaires à ceux que nous avons dans la fonction celsiusToFahrenheit() ( w = 1.8 et b = 32 ) puisque notre NanoNeuron a essayé de l'imiter.
console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}Évaluez la précision du modèle pour l'ensemble de données de test pour voir dans quelle mesure notre NanoNeuron gère les nouvelles prédictions de données inconnues. Le coût des prédictions sur les ensembles de tests devrait être proche du coût de la formation. Cela signifierait que notre NanoNeuron fonctionne bien sur les données connues et inconnues.
[ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023Maintenant, puisque nous voyons que notre "enfant" NanoNeuron a bien performé à "l'école" pendant l'entraînement et qu'il peut convertir correctement les températures Celsius en Fahrenheit, même pour les données qu'il n'a pas vues, nous pouvons l'appeler "intelligent". et posez-lui quelques questions. C’était le but ultime de tout le processus de formation.
const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158Si proche ! Comme nous tous, humains, notre NanoNeuron est bon mais pas idéal :)
Bon apprentissage à vous !
Vous pouvez cloner le référentiel et l'exécuter localement :
git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuronnode ./NanoNeuron.jsLes concepts d'apprentissage automatique suivants ont été ignorés et simplifiés pour simplifier l'explication.
Fractionnement des ensembles de données d'entraînement/test
Normalement, vous disposez d’un grand ensemble de données. En fonction du nombre d'exemples dans cet ensemble, vous souhaiterez peut-être le diviser dans une proportion de 70/30 pour les ensembles d'entraînement/test. Les données de l'ensemble doivent être mélangées de manière aléatoire avant la division. Si le nombre d'exemples est important (c'est-à-dire des millions), alors la répartition peut se produire dans des proportions plus proches de 90/10 ou 95/5 pour les ensembles de données d'entraînement/test.
Le réseau apporte le pouvoir
Normalement, vous ne remarquerez pas l’utilisation d’un seul neurone autonome. Le pouvoir réside dans le réseau de ces neurones. Le réseau pourrait apprendre des fonctionnalités beaucoup plus complexes. NanoNeuron à lui seul ressemble plus à une simple régression linéaire qu’à un réseau neuronal.
Normalisation des entrées
Avant la formation, il serait préférable de normaliser les valeurs d'entrée.
Implémentation vectorisée
Pour les réseaux, les calculs vectoriels (matriciels) fonctionnent beaucoup plus rapidement que for les boucles. Normalement, la propagation avant/arrière fonctionne beaucoup plus rapidement si elle est implémentée sous forme vectorisée et calculée à l'aide, par exemple, de la bibliothèque Numpy Python.
Minimum de la fonction de coût
La fonction de coût que nous utilisions dans cet exemple est trop simplifiée. Il devrait avoir des composantes logarithmiques. Changer la fonction de coût modifiera également ses dérivées, de sorte que l'étape de rétro-propagation utilisera également des formules différentes.
Fonction d'activation
Normalement, la sortie d'un neurone doit passer par une fonction d'activation comme Sigmoïde ou ReLU ou autres.