Le risque est un jeu de bourse de stratégie de diplomatie, de conflit et de conquête pour deux à six joueurs. Turn tourne parmi les joueurs qui contrôlent les armées de pièces de jeu avec lesquelles ils tentent de capturer des territoires d'autres joueurs, avec des résultats déterminés par des rouleaux de dés. Le but du jeu est d'occuper tous les territoires du tableau et, ce faisant, d'éliminer les autres joueurs. Chaque tour se compose de deux actions:
Le but de ce projet a été de mettre en œuvre le jeu de risques avec quelques modifications apportées dans les règles et de concevoir un agent artificiellement intelligent qui est capable de jouer correctement le jeu et d'avoir une très grande chance de gagner lorsqu'il fait face à d'autres adversaires, y compris à la fois humain réel joueurs ou autres joueurs d'agent.
Le jeu est implémenté à l'aide du langage de programmation Java. Contrôle des virages, effectuant des actions demandées par le joueur, mise à jour de la carte du jeu, vérification si tout se passe selon les règles, etc., sont les choses que fait cette partie du code. L'interface utilisateur de jeu est également conçue via des fichiers .fxml qui dessine la carte et est le lecteur de connexion à la plate-forme à la logique du jeu.
Cette section se concentre sur la mise en œuvre et l'évaluation des heuristiques qui mènent à une forte IA pour le risque de jeu.
L'implémentation est basée sur l'algorithme d'élagage Alpha-Beta Minimax. Le joueur construit un arbre de prédiction basé sur l'algorithme DFS.
Chaque fois que c'est le tour de l'agent de jouer, un arbre est fabriqué. Les nœuds d'arbre sont les états du jeu (carte du jeu dans cet état) et chaque bord est une attaque possible faite de l'état actuel au résultat de l'attaque de la carte. Une action d'attaque consiste en les coordonnées des territoires de départ et de cible et le nombre d'unités choisies pour être dans l'armée attaquante. Le nœud racine est l'état actuel de la carte dont un lecteur doit choisir ses mouvements. Bien que l'arbre ne puisse prédire qu'à l'état de fin du jeu en raison d'un grand nombre de mouvements possibles qu'un joueur peut avoir dans chaque état que la mémoire et les délais ne permettent pas. Par conséquent, le joueur ne peut construire l'arbre qu'à une certaine profondeur que nous avons définie dans le code. Il existe également des simplifications appliquées à des parties particulières de la stratégie de jeu de l'agent qui seront toutes expliquées dans les sections suivantes. Afin de prendre la meilleure décision possible, l'heuristique est définie pour les nœuds les plus profonds (feuilles d'arbres) qui évaluent la quantité d'atteinte à cet état peut être bénéfique pour le joueur. A déclaré que l'heuristique sera expliquée dans le rapport. Lorsque les valeurs des feuilles sont déterminées, l'arbre sera transmis à l'élagage alpha-bêta minimax et cet algorithme bien connu trouvera la meilleure série d'actions que le joueur peut avoir.
La fourniture d'unités aux territoires peut être une tâche délicate; Dans le sens où nous voulons améliorer notre pouvoir d'attaque, mais nous assurons également d'avoir un pouvoir de défense suffisant dans les territoires qui risquent d'être attaqués. Le déploiement d'unités dans des pays adjacents aux territoires ennemis pourrait être un moyen intelligent de maintenir l'équilibre entre ces deux objectifs.
Projet de simplification:
Prédire et inclure tous les scénarios de projet possibles dans l'arbre de prédiction conduira à un arbre complexe qui ferait face aux problèmes mentionnés précédemment; Par conséquent, l'une des simplifications faites est que nous utilisons une heuristique de rédaction qui s'est avérée avoir toujours le meilleur résultat possible et prédire que les adversaires font également cette approche en rédaction; En d'autres termes, nous supprimons les résultats de rédaction car les possibilités forment l'arborescence de prédiction et les modifions en scénarios de projet définitif.
Pour ce faire, nous prenons les mesures suivantes:
Braft heuristique:
Étape 1:
AKING La sommation de toutes les unités dans les pays ennemis, à côté du pays x, donnera une mesure que nous appelons la menace de sécurité des frontières (BST) en x.
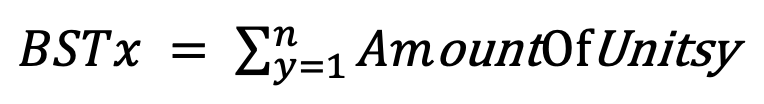
Étape 2:
La division de ce BST par les unités situées en x donne un rapport de sécurité des frontières (BSR) qui peut être comparée parmi tous les pays frontaliers.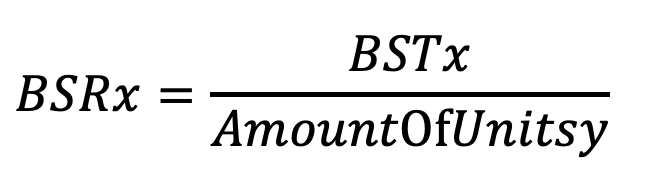
Les pays avec un BSR élevé sont plus susceptibles d'être conquis par un joueur ennemi, car le nombre d'unités ennemies dans les pays ennemis adjacents est relativement plus élevé que le nombre d'unités sur le pays lui-même. Choisir les pays avec un BSR élevé à fournir pour augmenter leur force défensive en abaissant le BSR. Fournir des unités à des pays un BSR inférieur, ce qui signifie qu'ils ont déjà une meilleure position défensive, augmentera leur force offensive, augmentant les chances d'une attaque réussie de ces pays.
Étape 3:
La normalisation du BSR en la divisant par la somme de tous les BSR des pays, un joueur possède, donnera une mesure directe par laquelle quelqu'un pourrait organiser des unités. Le rapport de sécurité des frontières normalisé (NBSR) est calculé par: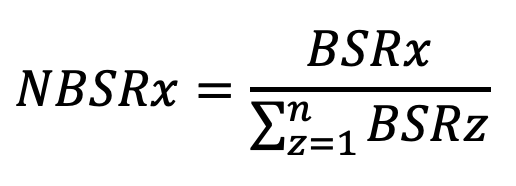
Il donne un rapport direct de la façon dont les unités pourraient être réparties entre les pays. À ce stade, nous pouvons voir qu'il y aurait un problème avec ces ratios car certaines données sont sans importance, et nous ne voulons pas ajouter d'unités à tous nos territoires, nous avons donc fixé un seuil entre les étapes deux et trois en triant les données BSRX dans Un ordre décroissant (nous nous concentrons davantage sur le renforcement de la puissance de défense), divisez les données du milieu et définissons les nombres dans la moitié inférieure à zéro.
Étape 4: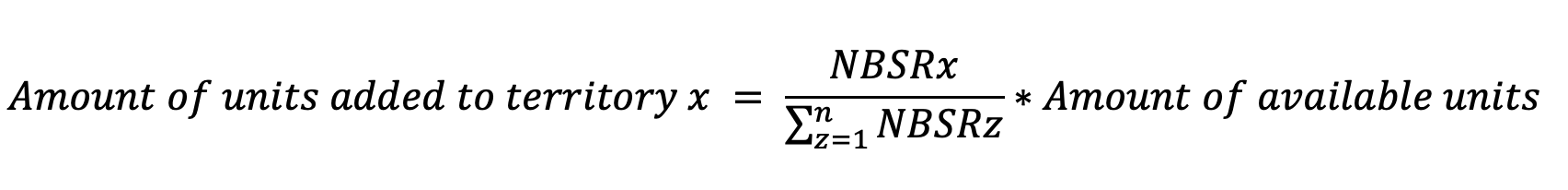
L'étape 4 se poursuivra jusqu'à ce qu'il ne reste plus d'unités disponibles à ajouter.
Il y a des simplifications appliquées dans la phase d'attaque afin de rendre l'arbre moins compliqué afin que nous puissions prédire à des niveaux plus profonds. Cela peut être fait en vérifiant quels scénarios d'attaque ont plus de chances de gagner la bataille et de les inclure dans l'arbre.
Afin d'évaluer à quel point une feuille d'arbre est bénéfique pour ce joueur spécifique; Nous avons défini quatre caractéristiques heuristiques que leurs meilleurs poids possibles sont trouvés lors de l'apprentissage de l'heuristique qui sera expliqué plus tard. Toutes les fonctionnalités renvoient un résultat entre zéro à un, car lorsque les fonctionnalités sont évaluées dans des rapports rapprochés les uns avec les autres, l'apprentissage et l'attribution de poids seraient plus précis.
Les fonctionnalités sont:
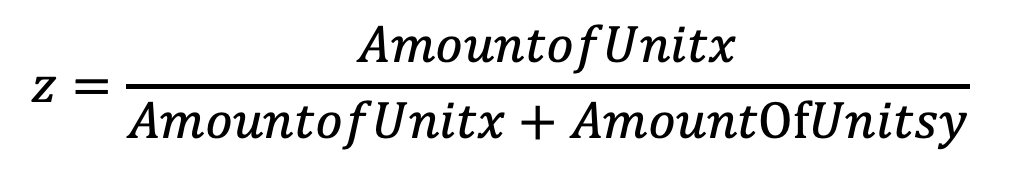
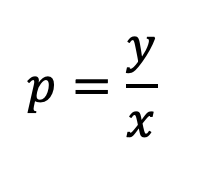
Donner du poids à chacune des heuristiques dans la partie précédente permet d'évaluer l'importance et l'influence de chacun d'eux pour un agent pour gagner le jeu. Le processus de recherche de ces poids est par génétique et apprendre. Chaque gène est un ensemble de quatre poids pour ces quatre caractéristiques. Nous commençons par générer 100 ensembles de poids aléatoires dans la plage [0,10]. Après cela, 10 tournois se produiront. Pour chaque tournoi, 10 gènes de la population primaire seront sélectionnés au hasard. Toutes les paires de gènes possibles joueront les unes contre les autres et le résultat de chaque jeu dans chaque tournoi sera documenté. La fonction de fitness est définie comme (nombre de victoires / nombre de jeux) pour chaque gène. Les trois gènes supérieurs de chaque tournoi (basé sur la fonction de fitness) seront sélectionnés, nous avons maintenant 30 gènes les plus sélectionnés. Parmi ceux-ci, nous sélectionnons 12 paires aléatoires et pour chaque paire, effectuez un crossover qui crée un nouveau gène en calculant le poids moyen de la paire de gènes. Par conséquent, nous avons maintenant 12 nouveaux gènes de ce croisement. D'un autre côté, 3 gènes sont sélectionnés au hasard dans les 30 gènes que nous avons eu et les muter en modifiant un poids aléatoire de chacun à un autre poids aléatoire dans la plage [0,10]. Après tout cela, nous avons maintenant 15 nouveaux gènes qui sont placés dans la population primaire, remplaçant les 15 moins bons que nous y avions déjà. À ce stade, la deuxième génération de gènes est générée. Ce processus continuera de se répéter jusqu'à ce que la génération 4 des gènes soit générée. Le gène supérieur de cette population sera sélectionné comme meilleur poids pour les caractéristiques de notre heuristique que l'agent utilisera pour jouer.