Il s'agit d'un petit programme qui analyse un enregistrement d'une montre ou d'une horloge et vous dit à quel point il fonctionne lente ou rapide. Vous pouvez l'utiliser pour réguler une montre mécanique en utilisant, par exemple, un téléphone portable pour enregistrer son tic-tac.
$ Python Fourier.py Recording.wav supposition initiale: 6,0 p / m 0,00606 Hz Devinez mis à jour: 5.9998549 P / M 1.88E-05 Hz L'erreur est de -2,1 secondes / jour
Le fichier recording.wav doit être un fichier son mono. Mon téléphone portable dispose d'un programme de «mémo vocale» qui enregistre l'audio à l'aide du microphone intégré. C'est très sensible à cet effet.
Avec un enregistrement de bonne qualité, vous verrez quelque chose comme ceci:
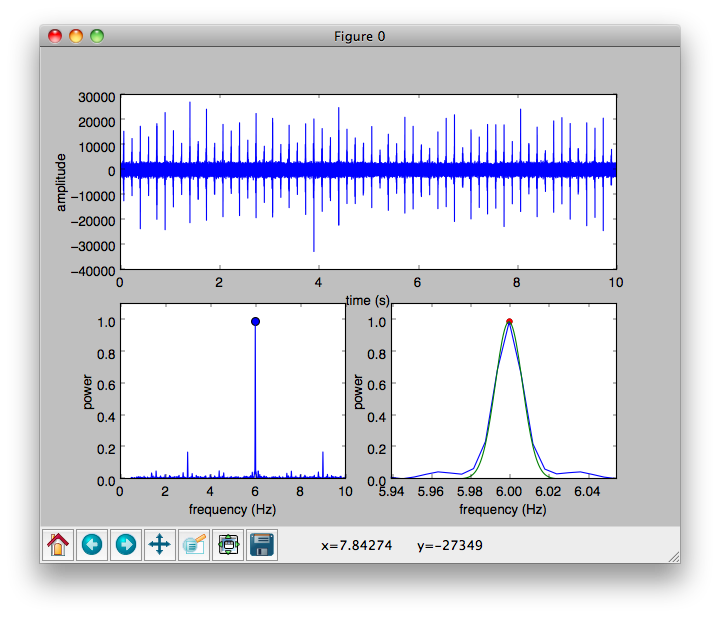
Le panneau supérieur montre les 10 dernières secondes de l'enregistrement… Cela vous permet d'évaluer la qualité de vos données. Ici, vous pouvez clairement voir les tiques individuelles, et que cette montre coche 6 fois par seconde. Le rapport signal / bruit est probablement 10 à environ dans cet exemple.
Le tracé en bas gauche montre la transformée de Fourier de l'enregistrement, zoomé dans la plage de 0,5 à 10 Hz. La pointe de ce tracé correspond à la fréquence de tic de la montre. Il est près de 6 tiques / par seconde, où ça devrait être… mais à quel point?
Le graphique en bas à droite montre un ajustement au pic, utilisé pour estimer la fréquence à une haute précision. Cette précision correspond facilement à la stabilité de la fréquence d'une montre mécanique (qui varie légèrement en raison des différences de température et d'orientation, entre autres).
Avec un enregistrement (très) de faible qualité, vous verrez plutôt quelque chose comme ceci:
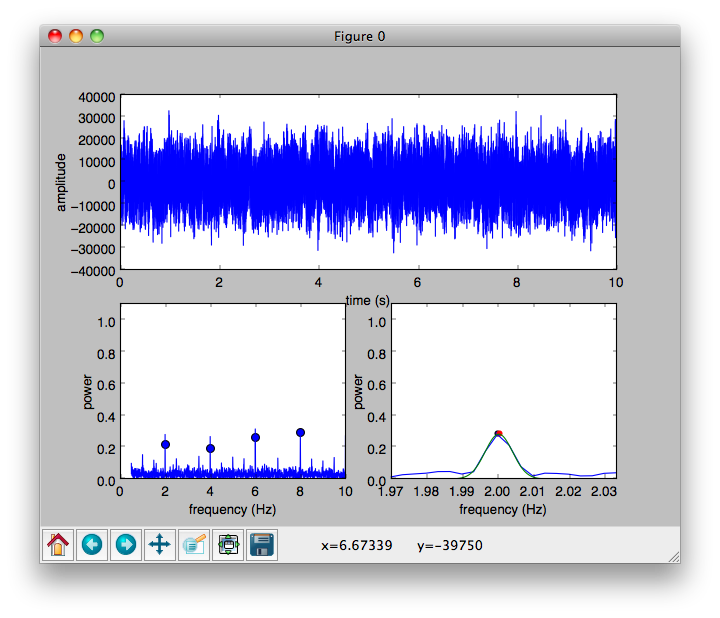
Ici, les tiques individuelles sont enterrées dans le bruit… mais le programme les choisit toujours! Vous avez cependant besoin d'un enregistrement plus long pour atteindre le même niveau de précision.
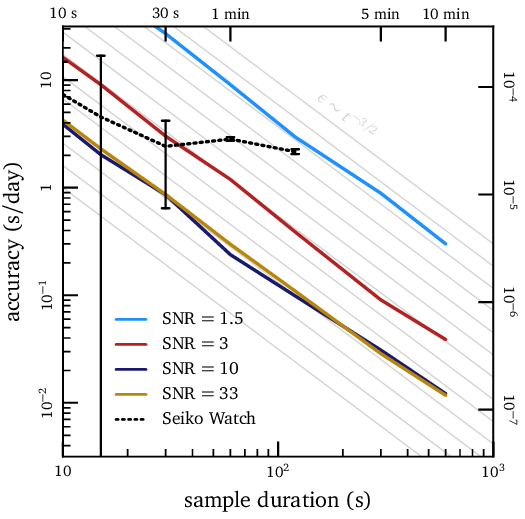
J'ai testé le programme à l'aide de signaux synthétiques générés de différentes manières. Les résultats sont résumés dans le tracé ci-dessus.
L'incertitude fractionnaire dans les échelles de mesure tombe avec la longueur de l'enregistrement à la puissance (3/2). Cela dépend également de la qualité de votre mesure. Ainsi, même si vous voulez faire un enregistrement aussi bon que possible, il peut être plus facile de compenser la qualité avec la quantité. Je trouve que 5 minutes de données de merde sont à peu près aussi bonnes que 30 secondes de données parfaites. Mais laisser votre montre et votre téléphone seul dans un tiroir à chaussettes pendant 5 minutes est beaucoup plus facile que de sortir et d'acheter un meilleur microphone. C'est donc à vous.
Si les données sont si mauvaises que vous ne pouvez même pas entendre des tiques dans l'enregistrement, vous pouvez avoir des ennuis, cependant. Rentez à nouveau dans un endroit plus calme ou trouvez un meilleur microphone. (Et, bien sûr, assurez-vous que votre horloge coche.)
La ligne noire en pointillés montre des mesures d'une vraie montre. Je voulais l'ajuster pour fonctionner avec quelques secondes par jour et j'ai trouvé un enregistrement de 30 secondes ou une minute a été suffisant pour la tâche. Vous poussez la barre du régulateur, enregistrez une minute, poussez à nouveau, et ainsi de suite jusqu'à ce que vous obteniez une réponse avec laquelle vous êtes satisfait. Je l'ai réglé à environ 2 secondes par jour, ce qui était mon objectif. Cela se traduit par une erreur inférieure à un centième de coche sur la durée de l'enregistrement, ce qui est assez impressionnant, je pense!
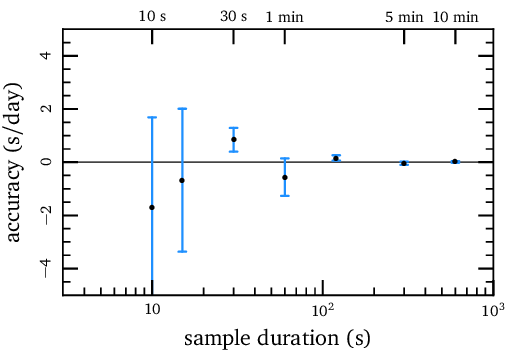
Le tracé ci-dessus montre un test à l'aide d'un signal synthétique «Tick» généré à l'aide de l'audace. Cela montre que l'incertitude rapportée par le programme est une représentation assez significative de l'incertitude «1-σ».
Le code est assez simple, et la plupart des efforts ont consisté à le faire fonctionner de manière prévisible sans aucune intervention humaine. I Fourier transforme le signal d'entrée pour mesurer la fréquence de pointe. Avant de transformer, je frappe le signal avec une fenêtre gaussienne… Je choisis la forme de la fenêtre de telle sorte que les pics de fréquence auront une forme gaussienne avec une largeur de ~ 3 bacs de fréquence. Cela peut être ajusté avec précision avec un profil gaussien, ce qui donne une bonne estimation de la véritable fréquence. Vous pouvez regarder les parcelles pour avoir une idée de la façon dont cela fonctionne.
J'utilise une fonction Scipy pour identifier automatiquement les pics, ce qui semble bien fonctionner.
Et j'essaie d'identifier une longueur «optimale» pour la FFT. Aucun problème avec cela jusqu'à présent.
Les résultats ne sont pas sensibles à la fréquence d'échantillonnage, à moins qu'il ne soit trop faible pour résoudre adéquatement le son de «coche» de l'horloge. Mais le programme fonctionne assez rapidement, il n'y a donc aucune raison de ne pas simplement utiliser le taux d'échantillonnage de 44,1 kHz qui est assez standard.