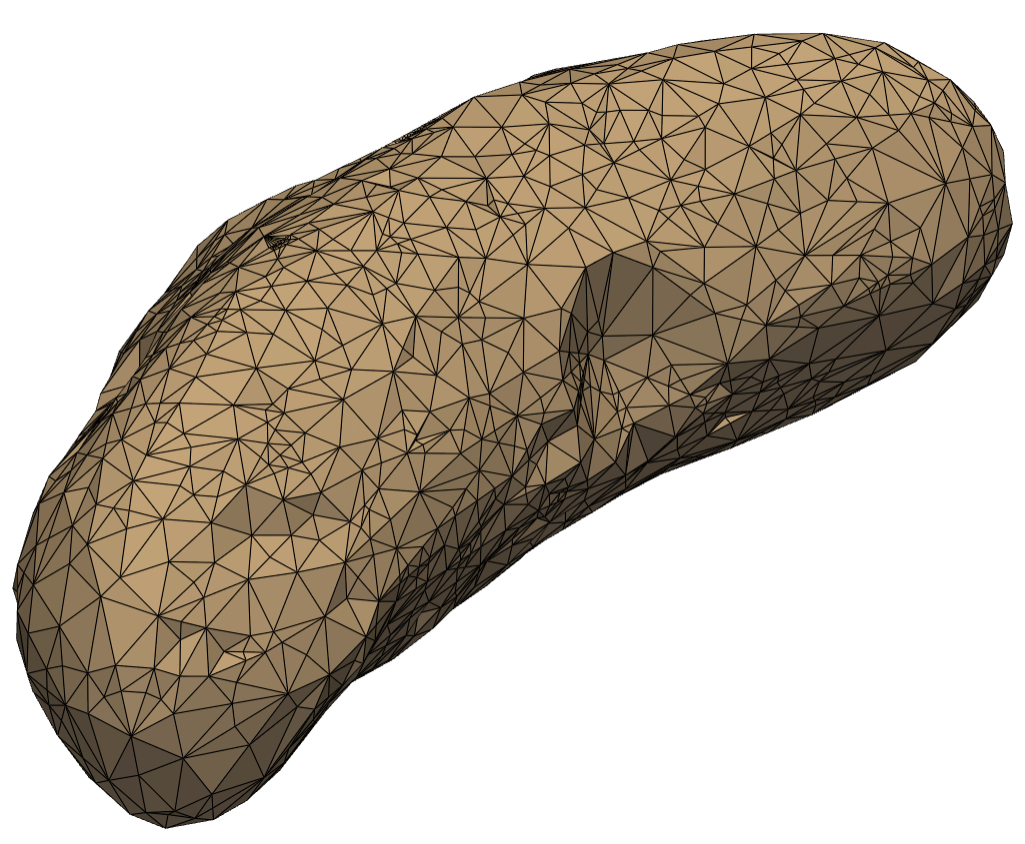
Mesh de (433) Eros avec 739 sommets et 1474 visages
Ce code est une implémentation validée dans C ++ 17 du modèle de gravité polyédrique par Tsoulis et al. De plus, le modèle fournit une liaison python. Il a été initialement créé dans un projet collaboratif entre Tu Munich et l'équipe Advanced Concepts d'ESA.
Si cette implémentation vous s'avère utile, veuillez envisager de citer l'article d'accompagnement publié dans le Journal of Open Source Software .
La mise en œuvre est basée sur le papier Tsoulis, D., 2012. Calcul analytique du tenseur de gravité complet d'une source polyédrique de forme arbitrairement arbitrairement en utilisant des intégrales de ligne. Géophysique, 77 (2), pp.f1-f11. et son implémentation correspondante dans Fortran.
Des détails supplémentaires peuvent être trouvés dans le papier plus récent Tsoulis, Dimitrios; Gavriilidou, Géorgie. Une revue de calcul de la formulation analytique intégrale de la ligne du signal de gravité polyédrique. Prospection géophysique, 2021, 69. Jg., Nr. 8-9, S. 1745-1760. et sa mise en œuvre correspondante dans MATLAB, qui est fortement basée sur l'ancienne implémentation dans Fortran.
Note
Les pages GitHub de ce projet contiennent la documentation complète complète de la bibliothèque C ++ et de l'interface Python ainsi que de l'arrière-plan sur le modèle Gravity et des paramètres avancés non détaillés ici.
L'évaluation du modèle de gravité polyédrique nécessite les paramètres suivants:
| Nom |
|---|
| Mesh polyédrique (soit comme sommets et visages, soit comme fichiers source polyédrique) |
| Densité constante |
Le maillage et l'unité de la densité des constantes doivent correspondre. Jetez un œil à la documentation pour afficher les fichiers de maillage pris en charge.
Le calcul sort les paramètres suivants pour chaque point de calcul p . Les unités de la sortie respective dépendent des unités des paramètres d'entrée (maillage et densité)! Par conséquent, si c'est par exemple votre maillage
| Nom | Unité (si je suis en train | Commentaire |
|---|---|---|
| Le potentiel ou également appelé énergie spécifique | ||
| L'accélération gravitationnelle dans les trois directions cartésiennes | ||
| Le taux spatial de variation de l'accélération gravitationnelle |
Note
La sortie de ce modèle de gravité obéit aux conventions de signe de la géodésie et de la géophysique. Par conséquent, le potentiel
L'exemple suivant montre comment utiliser l'interface Python pour calculer la gravité autour d'un cube:
import numpy as np
from polyhedral_gravity import Polyhedron , GravityEvaluable , evaluate , PolyhedronIntegrity , NormalOrientation
# We define the cube as a polyhedron with 8 vertices and 12 triangular faces
# The polyhedron's normals point outwards (see below for checking this)
# The density is set to 1.0
cube_vertices = np . array (
[[ - 1 , - 1 , - 1 ], [ 1 , - 1 , - 1 ], [ 1 , 1 , - 1 ], [ - 1 , 1 , - 1 ],
[ - 1 , - 1 , 1 ], [ 1 , - 1 , 1 ], [ 1 , 1 , 1 ], [ - 1 , 1 , 1 ]]
)
cube_faces = np . array (
[[ 1 , 3 , 2 ], [ 0 , 3 , 1 ], [ 0 , 1 , 5 ], [ 0 , 5 , 4 ], [ 0 , 7 , 3 ], [ 0 , 4 , 7 ],
[ 1 , 2 , 6 ], [ 1 , 6 , 5 ], [ 2 , 3 , 6 ], [ 3 , 7 , 6 ], [ 4 , 5 , 6 ], [ 4 , 6 , 7 ]]
)
cube_density = 1.0
computation_point = np . array ([ 0 , 0 , 0 ]) Nous définissons d'abord un polyèdre de densité constant des vertices et faces
cube_polyhedron = Polyhedron (
polyhedral_source = ( cube_vertices , cube_faces ),
density = cube_density ,
) Dans le cas où vous souhaitez remettre le polyèdre via un format de fichier pris en charge, remplacez simplement l'argument polyhedral_source par une liste de chaînes , où chaque chaîne est le chemin d'accès à un format de fichier pris en charge, par exemple polyhedral_source=["eros.node","eros.face"] ou polyhedral_source=["eros.mesh"] .
En continuant, le moyen le plus simple de calculer la gravité est d'utiliser la fonction evaluate :
potential , acceleration , tensor = evaluate (
polyhedron = cube_polyhedron ,
computation_points = computation_point ,
parallel = True ,
) Le moyen le plus avancé consiste à utiliser la classe GravityEvaluable . Il cache la structure et les propriétés des données internes qui peuvent être réutilisées pour plusieurs évaluations. Ceci est particulièrement utile si vous souhaitez calculer la gravité pour plusieurs points de calcul, mais ne connaissez pas les "points futurs" à l'avance.
evaluable = GravityEvaluable ( polyhedron = cube_polyhedron ) # stores intermediate computation steps
potential , acceleration , tensor = evaluable (
computation_points = computation_point ,
parallel = True ,
)
# Any future evaluable call after this one will be faster Notez que le computation_point pourrait également être un tableau en forme (n, 3) pour calculer plusieurs points à la fois. Dans ce cas, la valeur de retour de evaluate(..) ou une GravityEvaluable sera une liste de triplets comprenant du potentiel, de l'accélération et du tenseur.
Le modèle de gravité nécessite que toutes les normales de l'unité plane du polyèdre pointent systématiquement vers l'extérieur ou vers l'intérieur du polyèdre. Vous pouvez le spécifier via la normal_orientation . Cette propriété est - par défaut - vérifiée lors de la construction du Polyhedron ! Alors, ne vous inquiétez pas, il est impossible sinon explicitement désactivé de créer un Polyhedron non valide. Vous pouvez désactiver / activer ce paramètre via l'indicateur integrity_check en option et peut même réparer automatiquement la commande via HEAL . Si vous êtes convaincu que votre maillage est défini correctement (par exemple, vérifié une fois avec le chèque d'intégrité), vous pouvez désactiver ce chèque (via DISABLE ) pour éviter les frais généraux supplémentaires du chèque.
cube_polyhedron = Polyhedron (
polyhedral_source = ( cube_vertices , cube_faces ),
density = cube_density ,
normal_orientation = NormalOrientation . INWARDS , # OUTWARDS (default) or INWARDS
integrity_check = PolyhedronIntegrity . VERIFY , # VERIFY (default), DISABLE or HEAL
)Conseil
Plus d'exemples et de parcelles sont représentés dans le cahier Jupyter.
L'exemple suivant montre comment utiliser la bibliothèque C ++ pour calculer la gravité. Il fonctionne de manière analogue à l'exemple Python ci-dessus.
// Defining the input like above in the Python example
std::vector<std::array< double , 3 >> vertices = ...
std::vector<std::array< size_t , 3 >> faces = ...
double density = 1.0 ;
// The constant density polyhedron is defined by its vertices & faces
// It also supports the hand-over of NormalOrientation and PolyhedronIntegrity as optional arguments
// as above described for the Python Interface
Polyhedron polyhedron{vertices, faces, density};
std::vector<std::array< double , 3 >> points = ...
std::array< double , 3 > point = points[ 0 ];
bool parallel = true ; La bibliothèque C ++ fournit également deux façons de calculer la gravité. Via la fonction libre evaluate ...
const auto [pot, acc, tensor] = GravityModel::evaluate(polyhedron, point, parallel); ... ou via la classe GravityEvaluable .
// Instantiation of the GravityEvaluable object
GravityEvaluable evaluable{polyhedron};
// From now, we can evaluate the gravity model for any point with
const auto [potential, acceleration, tensor] = evaluable(point, parallel);
// or for multiple points with
const auto results = evaluable(points, parallel);De façon similaire à Python, l'implémentation C ++ fournit également des capacités de vérification de maillage.
Conseil
Pour référence, jetez un œil à la méthode principale de l'exécutable C ++.
L'interface Python peut être facilement installée avec Conda:
conda install -c conda-forge polyhedral-gravity-modelEn deuxième option, vous pouvez également installer l'interface Python avec PIP de PYPI.
pip install polyhedral-gravity Des binaires pour les plates-formes les plus courantes sont disponibles sur PYPI, notamment Windows, Linux et MacOS. Pour MacOS et Linux, des binaires pour x86_64 et aarch64 sont fournis. Dans le cas où pip utilise la distribution des sources, veuillez vous assurer que vous avez installé un compilateur et CMake capables C ++ 17.
Le projet utilise les dépendances suivantes, toutes sont automatiquement configurées via Cmake:
atan(..)Le module sera construit à l'aide d'un compilateur capable C ++ 17, CMake. Exécutez simplement la commande suivante dans le dossier racine du référentiel:
pip install . Pour modifier les options de construction (comme la parallélisation), jetez un œil au paragraphe suivant. Les options sont modifiées en définissant les variables d'environnement avant d'exécuter l' pip install . Commande, par exemple:
export POLYHEDRAL_GRAVITY_PARALLELIZATION= " TBB "
pip install .(Facultatif: pour une construction plus rapide, vous pouvez installer toutes les dépendances disponibles pour votre système dans votre environnement Python local. De cette façon, ils ne seront pas récupérés à partir de GitHub.)
Le programme est construit en utilisant CMake. Assurez-vous d'abord que vous avez installé Cmake, puis suivez ces étapes:
mkdir build
cd build
cmake .. < options >
cmake --build .Les options suivantes sont disponibles:
| Nom (par défaut) | Options |
|---|---|
Polyédre_gravity_parsallilization ( CPP ) | CPP = exécution série / OMP ou TBB = exécution parallèle avec OpenMP ou Intel TBB |
Logging_level ( INFO ) | TRACE , DEBUG , INFO , WARN , ERROR , CRITICAL , OFF |
Build_polyeddral_gravity_docs ( OFF ) | Construire cette documentation |
Build_polyeddral_gravity_tests ( ON ) | Construire les tests |
Build_polyeddral_python_interface ( ON ) | Construire l'interface Python |
Pendant le test PolyEdral_Gravity_Parallilization = TBB a été le plus performant. Il n'est pas en outre recommandé de changer le logging_level en autre chose que INFO=2 .
Les paramètres CMake recommandés utilisant le backend TBB ressembleraient à ceci:
cmake .. -POLYHEDRAL_GRAVITY_PARALLELIZATION= " TBB "Après la construction, le modèle de gravité peut être exécuté en exécutant:
./polyhedralGravity < YAML-Configuration-File > où le fichier de configuration YAML contient les paramètres requis. Des exemples de fichiers de configuration et de fichiers source polyédrique peuvent être trouvés dans ce référentiel dans le dossier /example-config/ .
La configuration doit ressembler à l'exemple donné ci-dessous. Il est nécessaire de spécifier les fichiers source du maillage du polyèdre (plus d'informations sur le fichier pris en charge dans la documentation), la densité du polyèdre et les points de calcul souhaités où le tenseur de gravité doit être calculé. Il faut en outre spécifier le nom du fichier de sortie .csv.
---
gravityModel :
input :
polyhedron : # polyhedron source-file(s)
- " ../example-config/data/tsoulis.node " # .node contains the vertices
- " ../example-config/data/tsoulis.face " # .face contains the triangular faces
density : 2670.0 # constant density, units must match with the mesh (see section below)
points : # Location of the computation point(s) P
- [ 0, 0, 0 ] # Here it is situated at the origin
check_mesh : true # Fully optional, enables mesh autodetect+repair of
# the polyhedron's vertex ordering (not given: true)
output :
filename : " gravity_result.csv " # The name of the output file
L'exécutable produit un fichier CSV contenant
Le projet utilise Googlest pour les tests. Dans Oder pour exécuter ces tests, exécutez simplement la commande suivante dans le répertoire de construction:
ctestPour la suite de test Python, veuillez exécuter la commande suivante dans le dossier racine du référentiel:
pytestNous sommes heureux d'accepter les contributions au projet sous forme de suggestions, de rapports de bogues et de demandes de traction. Veuillez consulter les directives contributives pour plus d'informations.