Pengambilan sampel ulang Lanczos (diucapkan Lanchos) adalah teknik canggih untuk menginterpolasi sinyal digital, menawarkan kualitas gambar yang unggul dibandingkan dengan metode sederhana seperti tetangga terdekat dan interpolasi bilinear. Dengan menjaga detail secara efektif dan meminimalkan artefak aliasing, pengambilan sampel ulang Lanczos banyak digunakan dalam aplikasi pemrosesan gambar dan sinyal.
Meskipun Lanczos unggul dalam kualitas gambar, hal ini harus mengorbankan kompleksitas komputasi yang meningkat. Selain itu, potensi artefak "berdering", terutama di sekitar tepi tajam, dapat menjadi kelemahan. Terlepas dari tantangan ini, Lanczos tetap menjadi pilihan utama untuk tugas-tugas seperti penskalaan dan rotasi gambar karena keunggulan kinerjanya secara keseluruhan.
Dokumen ini memberikan gambaran komprehensif tentang pengambilan sampel ulang Lanczos, termasuk dasar teoritisnya, rincian implementasi, dan aplikasi praktisnya. Ini berfungsi sebagai sumber berharga bagi pengembang dan peneliti yang ingin memahami dan memanfaatkan teknik canggih ini. Bagian selanjutnya mempelajari aspek-aspek penting dari pengambilan sampel ulang Lanczos, seperti kernel Lanczos, proses interpolasi dan pengambilan sampel ulang, pelestarian fluks, upsampling, downsampling, pemosisian sampel, rentang keluaran, interpolasi multidimensi, dan keterpisahan. Contoh praktis disertai kode sumber disertakan.
Kernel Lanczos, yang ditentukan untuk ukuran dukungan tertentu, adalah fungsi yang digunakan dalam pengambilan sampel ulang Lanczos. Kernel didefinisikan sebagai:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Di mana:
Fungsi sinc yang dinormalisasi didefinisikan sebagai:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
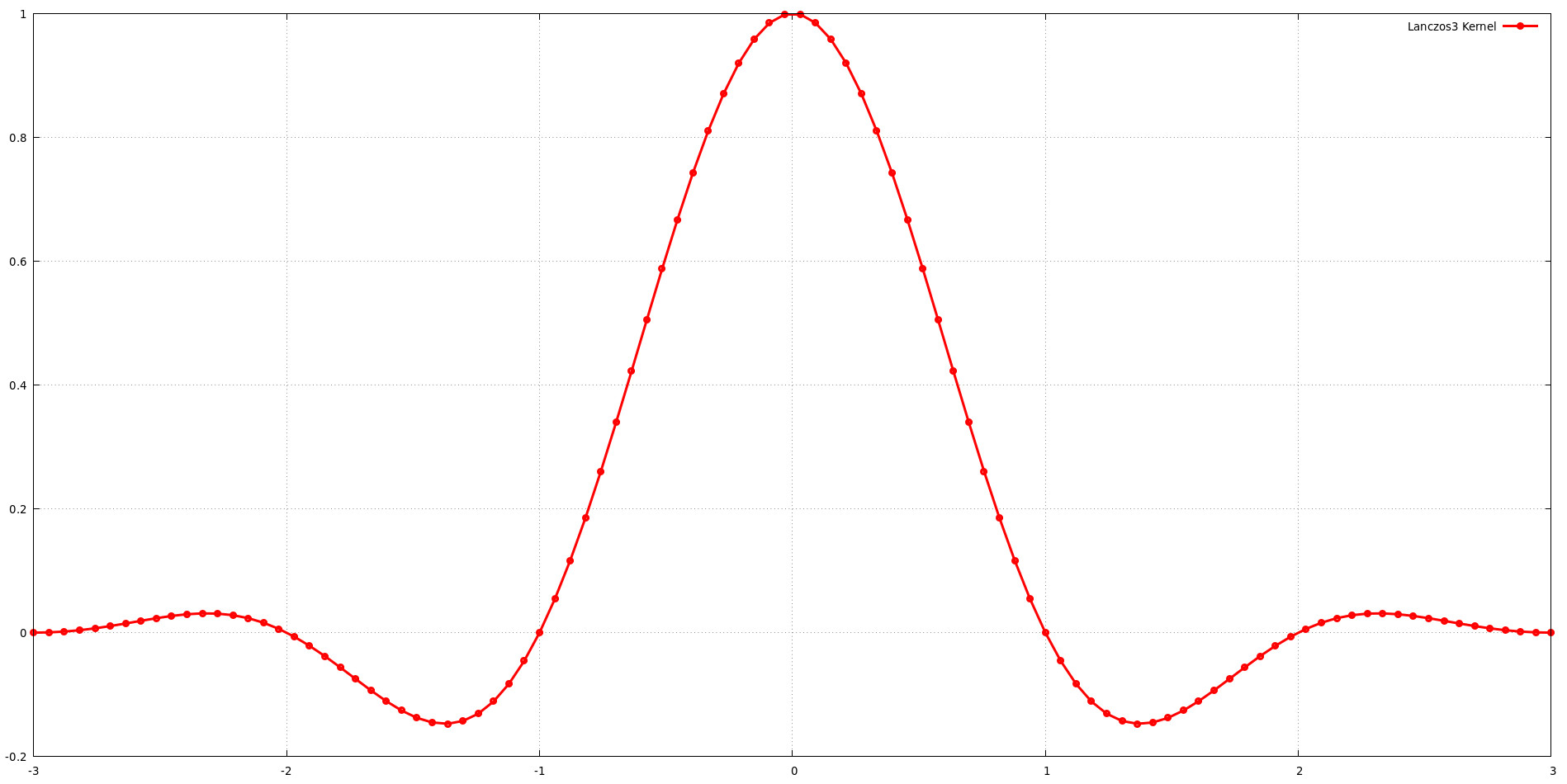
Grafik mengilustrasikan bentuk kernel Lanczos untuk ukuran dukungan a = 3. Ini berarti kernel mencakup tiga lobus fungsi sinc. Meskipun meningkatkan ukuran dukungan (a) umumnya memberikan lebih banyak fleksibilitas untuk membentuk respons frekuensi, hal ini juga meningkatkan biaya komputasi. Keseimbangan harus dicapai antara kualitas gambar dan efisiensi komputasi saat memilih ukuran dukungan. Temuan Jim Blinn bahwa kernel Lanczos dengan a = 3 menawarkan keseimbangan yang sangat baik antara pelestarian frekuensi rendah dan penolakan frekuensi tinggi mendukung gagasan ini.
Catatan: Istilah "lebar kernel", "ukuran dukungan", dan "ukuran filter" sering digunakan secara bergantian untuk menjelaskan parameter a. Namun, dalam konteks pengambilan sampel ulang Lanczos, "ukuran dukungan" paling akurat mencerminkan konsep tersebut.
Interpolasi Lanczos adalah teknik yang digunakan untuk mengambil sampel ulang sinyal diskrit ke tingkat pengambilan sampel baru. Hal ini dicapai dengan menggabungkan sinyal asli dengan kernel Lanczos.
Sinyal interpolasi s2(x) dapat dihitung sebagai berikut:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Di mana:
Mempertahankan Fluks:
Faktor normalisasi w(x) sangat penting untuk menjaga energi atau massa sinyal secara keseluruhan selama proses interpolasi. Ini memastikan bahwa jumlah nilai yang diinterpolasi mendekati jumlah sampel asli. Berat filter dihitung sebagai:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Pengambilan sampel:
Saat meningkatkan laju pengambilan sampel, persamaan interpolasi Lanczos dapat digunakan secara langsung tanpa modifikasi.
Pengambilan sampel yang lebih rendah:
Untuk menghindari artefak aliasing saat menurunkan laju pengambilan sampel, skala filter harus disesuaikan agar sesuai dengan laju pengambilan sampel yang baru.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Di mana:
Saat mengambil sampel ulang sinyal dari n1 sampel ke n2 sampel, posisi sampel berikut digunakan. Indeks j digunakan untuk mewakili sampel dari sinyal sampel s2(x). Suku (j + 0,5) adalah pusat sampel dalam s2(x). Langkah ini menskalakan suatu titik di s2(x) ke suatu titik di s1(x). Suku -0,5 terakhir dalam x adalah pergeseran fasa yang menyebabkan sampel koefisien Lanczos diimbangi.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Saat melakukan interpolasi Lanczos, perhatian khusus harus diberikan pada batas sinyal. Teknik penanganan tepi yang umum meliputi:
Bantalan Nol:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Menjepit:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
Penjepitan sering kali lebih disukai karena mengurangi artefak tepi yang disebabkan oleh diskontinuitas tajam di dekat tepian. Namun, pilihan metode penanganan tepi bergantung pada aplikasi spesifik dan keluaran yang diinginkan.
Kisaran s2(x) mungkin lebih besar dari s1(x) karena lobus L(x). Misalnya, sinyal input s1(x) yang sesuai dengan warna piksel dalam rentang [0.0,1.0] perlu dijepit ke rentang yang sama untuk memastikan bahwa nilai output tidak meluap ketika dikonversi kembali ke byte yang tidak ditandatangani [0,255] .
Kernel Lanczos dapat diperluas ke beberapa dimensi untuk melakukan interpolasi pada gambar atau data berdimensi lebih tinggi.
Kernel Lanczos dua dimensi didefinisikan sebagai:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
Sinyal interpolasi s2(x, y) dapat dihitung menggunakan rumus berikut:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Dimana w(x, y) adalah faktor normalisasi yang dihitung menggunakan kernel Lanczos dua dimensi.
Tidak seperti beberapa metode interpolasi, kernel Lanczos tidak dapat dipisahkan, artinya tidak dapat difaktorkan ke dalam produk kernel satu dimensi. Properti ini umumnya menyebabkan biaya komputasi yang lebih tinggi dibandingkan dengan kernel yang dapat dipisahkan. Untuk meningkatkan kinerja, beberapa implementasi mendekati kernel Lanczos dengan melakukan lintasan terpisah untuk dimensi horizontal dan vertikal.
Interpolasi Horisontal:
Interpolasi Vertikal:
Representasi Matematika:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Perhatikan bahwa faktor normalisasi w(x) dan w(y) dihitung menggunakan kernel Lanczos satu dimensi.
Poin Penting:
Demikian pula, pengambilan sampel ulang sinyal secara rekursif beberapa kali, seperti yang biasa dilakukan untuk menghasilkan peta mip tekstur, juga dapat menurunkan kualitas gambar karena akumulasi kesalahan dari setiap langkah pengambilan sampel ulang.
Jalankan contoh uji lancos dan gunakan gnuplot untuk melihat bagaimana pengambilan sampel ulang Lanczos memengaruhi sinyal satu dimensi sederhana ketika sampelnya ditingkatkan dan diturunkan sampelnya dengan faktor 2.
make
./lanczos-test
gnuplot
> load "output.plot"
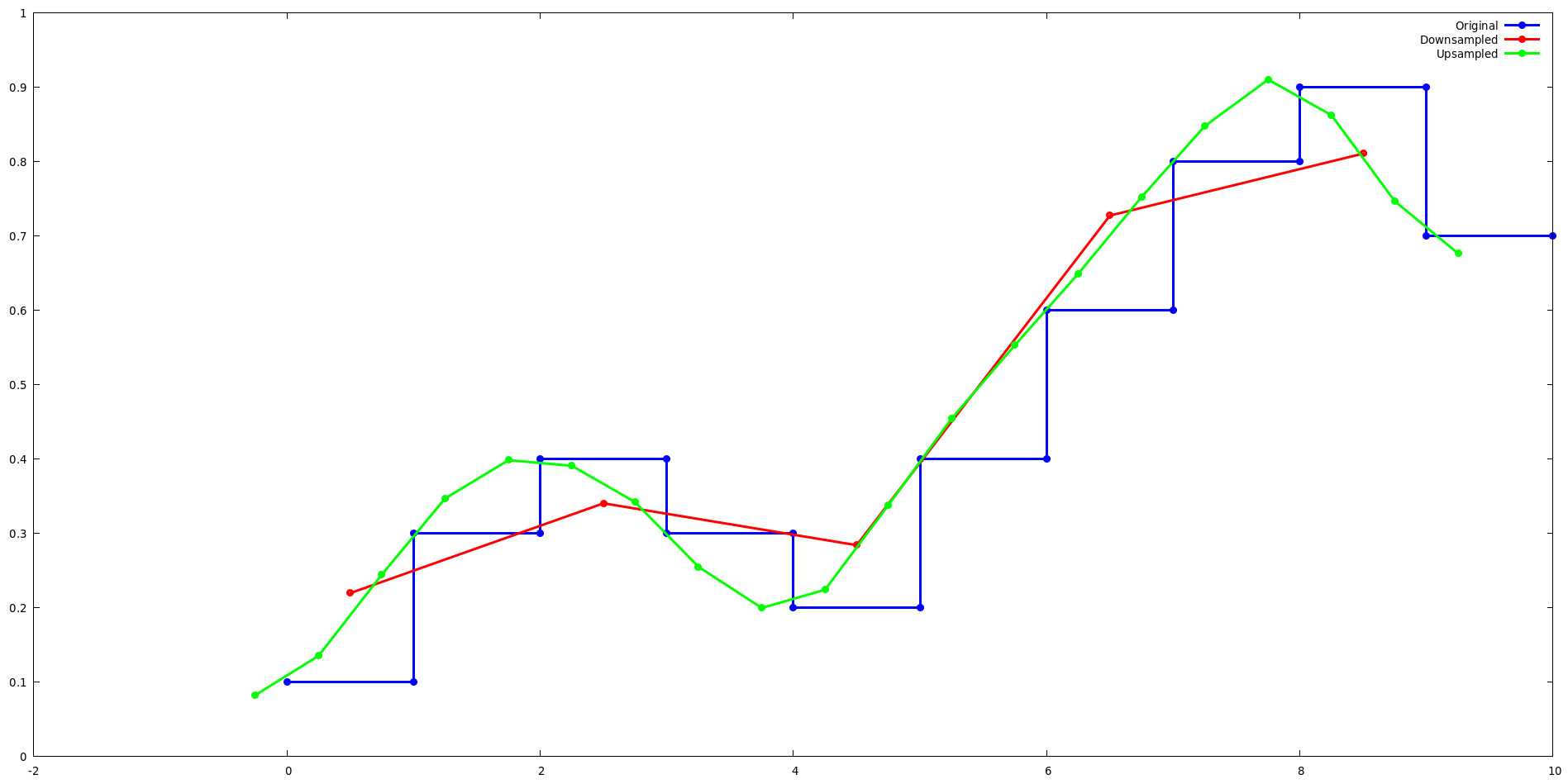
Pengambilan sampel:
Saat melakukan upsampling dengan kekuatan dua, kernel Lanczos melakukan siklus antara kumpulan nilai 2^level. Misalnya, perhatikan 4 output pertama dari contoh upsample lanzcos-test. Perhatikan bahwa keluaran untuk L(x) berulang untuk j={0,2} dan j={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Pengambilan sampel yang lebih rendah:
Saat melakukan downsampling dengan pangkat dua, kernel Lanczos menjadi tidak bergantung pada x karena (x - floor(x)) menjadi konstanta yang sesuai dengan pergeseran fasa. Misalnya, perhatikan 2 keluaran pertama dari contoh downsample uji lanzcos. Perhatikan bahwa keluaran L(x) berulang untuk setiap j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
Sebagai optimasi lebih lanjut, kernel Lanczos mungkin telah dihitung sebelumnya untuk kasus ini guna menghilangkan komputasi fungsi sinc yang mahal.
README ini dibuat dengan bantuan Google Gemini.
Referensi tambahan meliputi:
Kode ini diterapkan oleh Jeff Body di bawah Lisensi MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.