greta.gam: Model aditif umum di greta menggunakan mgcv

greta.gam memungkinkan Anda menggunakan fungsi halus mgcv dan sintaks rumus untuk menentukan istilah halus untuk digunakan dalam model greta. Anda kemudian dapat menentukan kemungkinan Anda sendiri untuk menyelesaikan model, dan menyesuaikannya dengan MCMC.

Ini sedang dalam proses!

Contoh

Berikut ini contoh sederhana yang diadaptasi dari file bantuan mgcv ?gam :

Dalam mgcv :

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

Sekarang memasang model yang sama di greta :

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )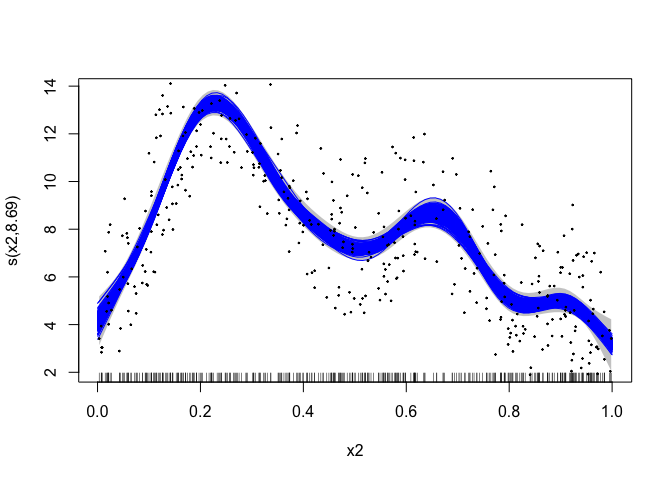

Detail teknis singkat

greta.gam menggunakan beberapa trik dari rutinitas jagam (Wood, 2016) di mgcv agar semuanya berfungsi. Berikut adalah beberapa detail singkat bagi mereka yang tertarik dengan cara kerja internal…

Interpretasi Bayesian terhadap GAM

GAM adalah model dengan interpretasi Bayesian (walaupun dilengkapi dengan metode “frequentist”). Matriks penalti yang lebih halus dapat dianggap sebagai matriks presisi sebelumnya dalam model efek acak Bayesian. Matriks desain dibuat persis seperti dalam kasus frequentist. Lihat Miller (2021) untuk latar belakang lebih lanjut mengenai hal ini.

Matriks penalti

Ada sedikit kesulitan dalam penafsiran Bayesian terhadap GAM karena, dalam bentuknya yang naif, prior tidak tepat sebagai ruang kosong dari hukuman (dalam kasus 1D, biasanya istilah linier). Untuk mendapatkan prior yang tepat, kita dapat menggunakan salah satu “trik” yang digunakan dalam Marra & Wood (2011) – yaitu memberikan penalti pada bagian penalti yang mengarah pada prior yang tidak tepat. Kami mengambil opsi yang disediakan oleh jagam dan membuat matriks penalti tambahan untuk ketentuan ini (dari dekomposisi eigen matriks penalti; lihat Marra & Wood, 2011).