Beranda | Instalasi | Dokumentasi | Tutorial | Pengembang
rodeo adalah pustaka Python cepat yang menggunakan numerik probabilistik untuk menyelesaikan persamaan diferensial biasa (ODE). Artinya, sebagian besar pemecah ODE (seperti metode Euler) menghasilkan perkiraan deterministik terhadap ODE pada grid dengan ukuran langkah
rodeo memberikan rangkaian perkiraan yang ringan dan dapat diperluas ke paradigma pemfilteran Bayesian nonlinier yang umum bagi banyak pemecah probabilistik (Tronarp dkk (2018)). Ini dimulai dengan menempatkan proses Gaussian sebelum solusi ODE, dan memperbaruinya secara berurutan seiring langkah pemecah melalui grid. rodeo dibangun di atas jax yang memungkinkan kompilasi just-in-time dan diferensiasi otomatis. API jax hampir setara dengan numpy .
rodeo menyediakan dua alat utama: satu untuk memperkirakan solusi ODE dan yang lainnya untuk inferensi parameter. Untuk yang pertama kami menyediakan:
solve : Implementasi pemecah ODE probabilistik yang menggunakan paradigma pemfilteran Bayesian nonlinier.Untuk yang terakhir kami menyediakan metode perkiraan kemungkinan:
basic : Implementasi metode perkiraan kemungkinan dasar (detailnya dapat ditemukan di Wu dan Lysy (2023)).fenrir : Implementasi Fenrir (Tronarp dkk (2022)).marginal_mcmc : implementasi MCMC dari metode Chkrebtii (Chkrebtii et al (2016)).dalton : Implementasi perkiraan kemungkinan ODE adaptif data kami (Wu dan Lysy (2023)).Contoh rinci penggunaannya dapat ditemukan di bagian Dokumentasi. Harap dicatat bahwa ini adalah rodeo versi jax saja. Untuk versi lawas yang menggunakan berbagai backend lain silakan lihat di sini.
Unduh repo dari GitHub lalu instal dengan skrip setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Silakan buka readthedocs terlebih dahulu untuk melihat dokumentasi yang diberikan untuk contoh berikut.
Tutorial memulai cepat tentang memecahkan masalah ODE sederhana.
Contoh penyelesaian ODE tingkat tinggi.
Contoh penyelesaian ODE chaos yang sulit.
Contoh masalah inferensi parameter dimana kita menggunakan pendekatan Laplace.
Dalam panduan ini, kami menunjukkan cara menyelesaikan ODE dengan pemecah probabilistik dan melakukan inferensi parameter. Pertama-tama kami akan mengilustrasikan pengaturan untuk menyelesaikan ODE. Untuk itu, mari kita perhatikan contoh ODE urutan pertama berikut (model FitzHugh-Nagumo ),
dimana solusinya
Mengikuti notasi (Wu dan Lysy (2023)), kita punya
untuk
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Kami membandingkan solusi dari solver dengan solusi deterministik yang disediakan oleh odeint di perpustakaan scipy .
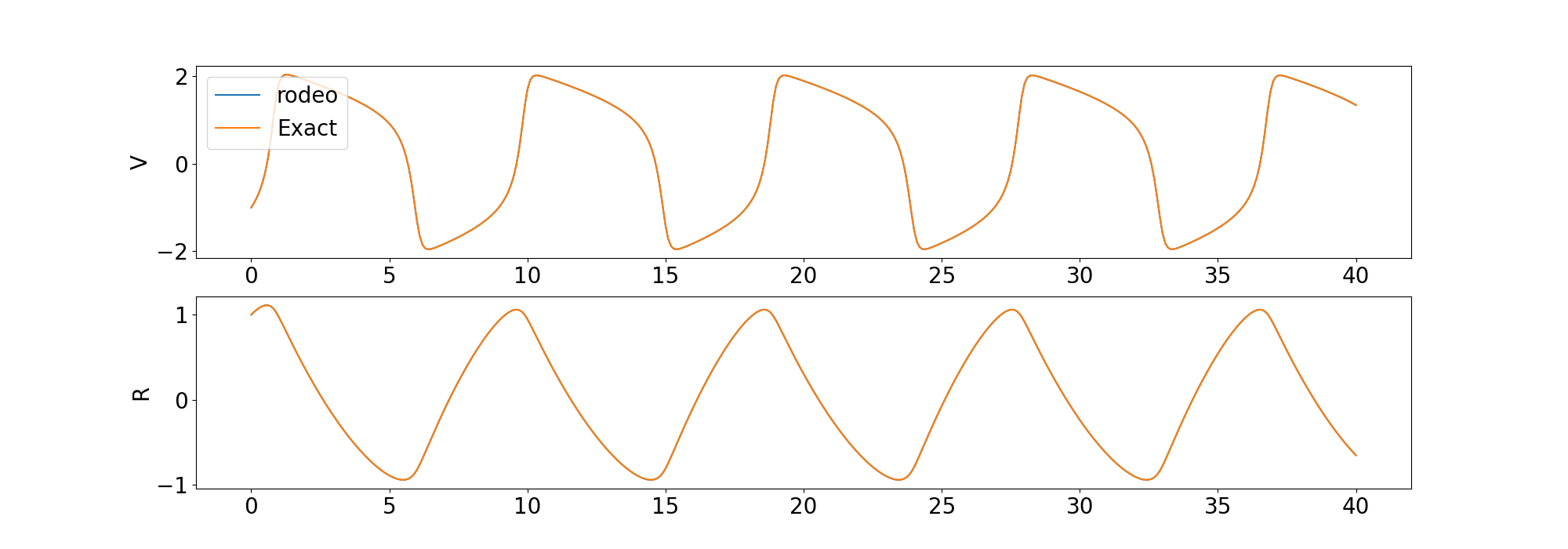
Kami juga menyertakan contoh untuk menyelesaikan ODE tingkat tinggi dan ODE chaos.
Kami sekarang beralih ke masalah inferensi parameter. rodeo berisi beberapa metode perkiraan kemungkinan yang dirangkum di bagian Deskripsi. Di sini, kita akan menggunakan metode perkiraan kemungkinan basic . Misalkan observasi disimulasikan melalui model
Di mana basic
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Ini adalah contoh dasar untuk menunjukkan penggunaan. Kami menyarankan perkiraan kemungkinan yang lebih canggih yang menyebarkan ketidakpastian solusi ke perkiraan kemungkinan seperti fenrir , marginal_mcmc dan dalton . Silakan merujuk ke tutorial inferensi parameter untuk lebih jelasnya.
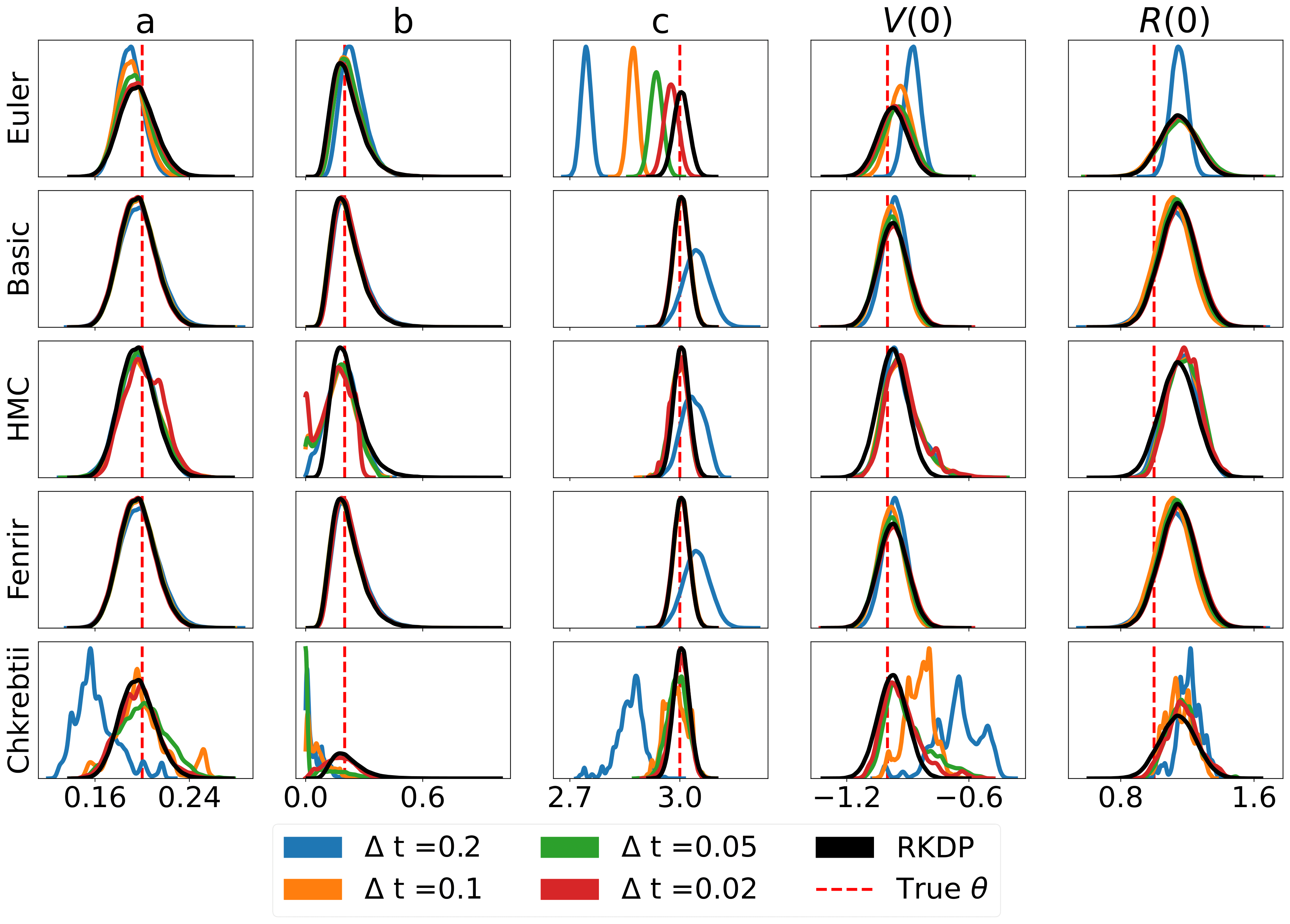
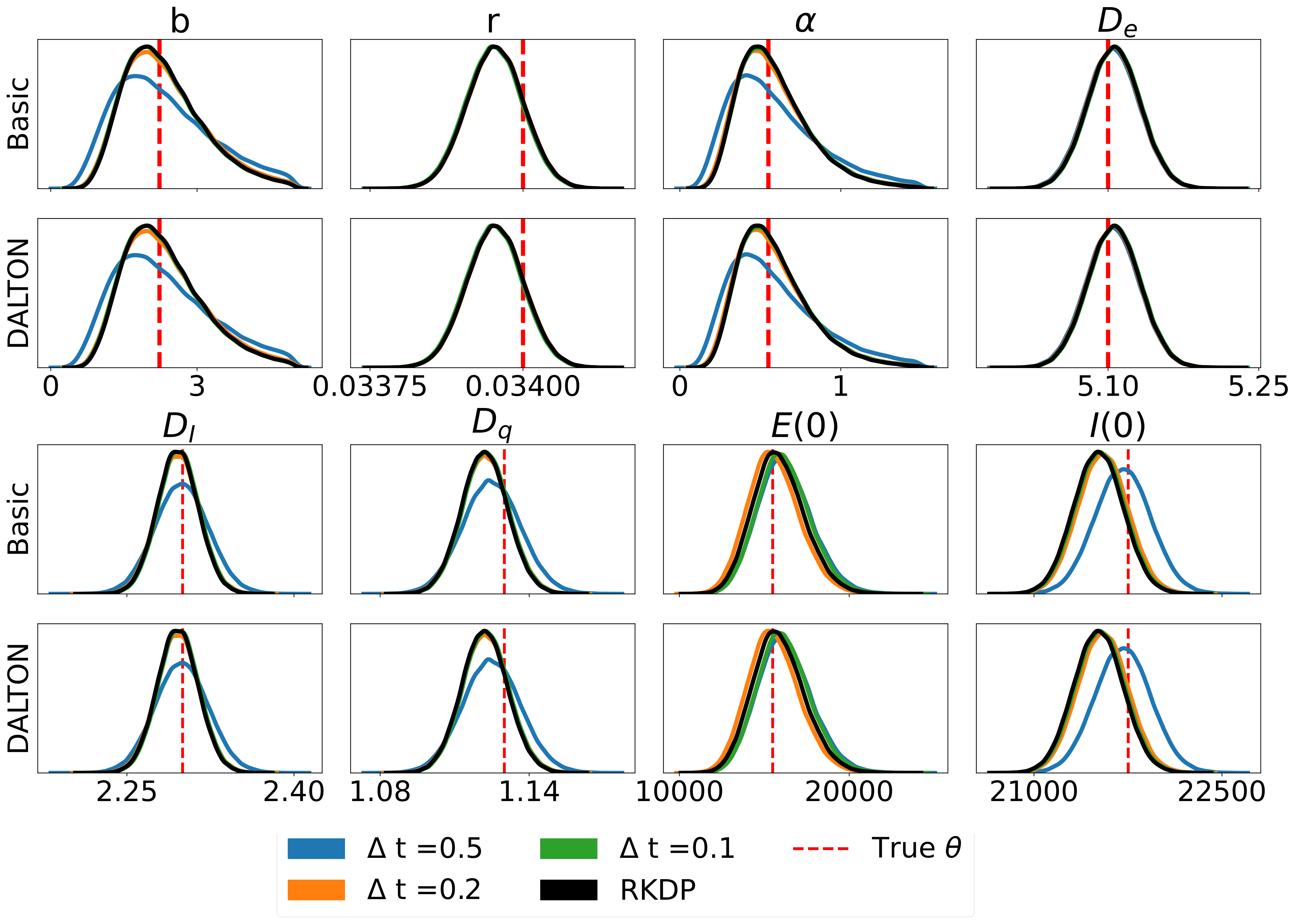
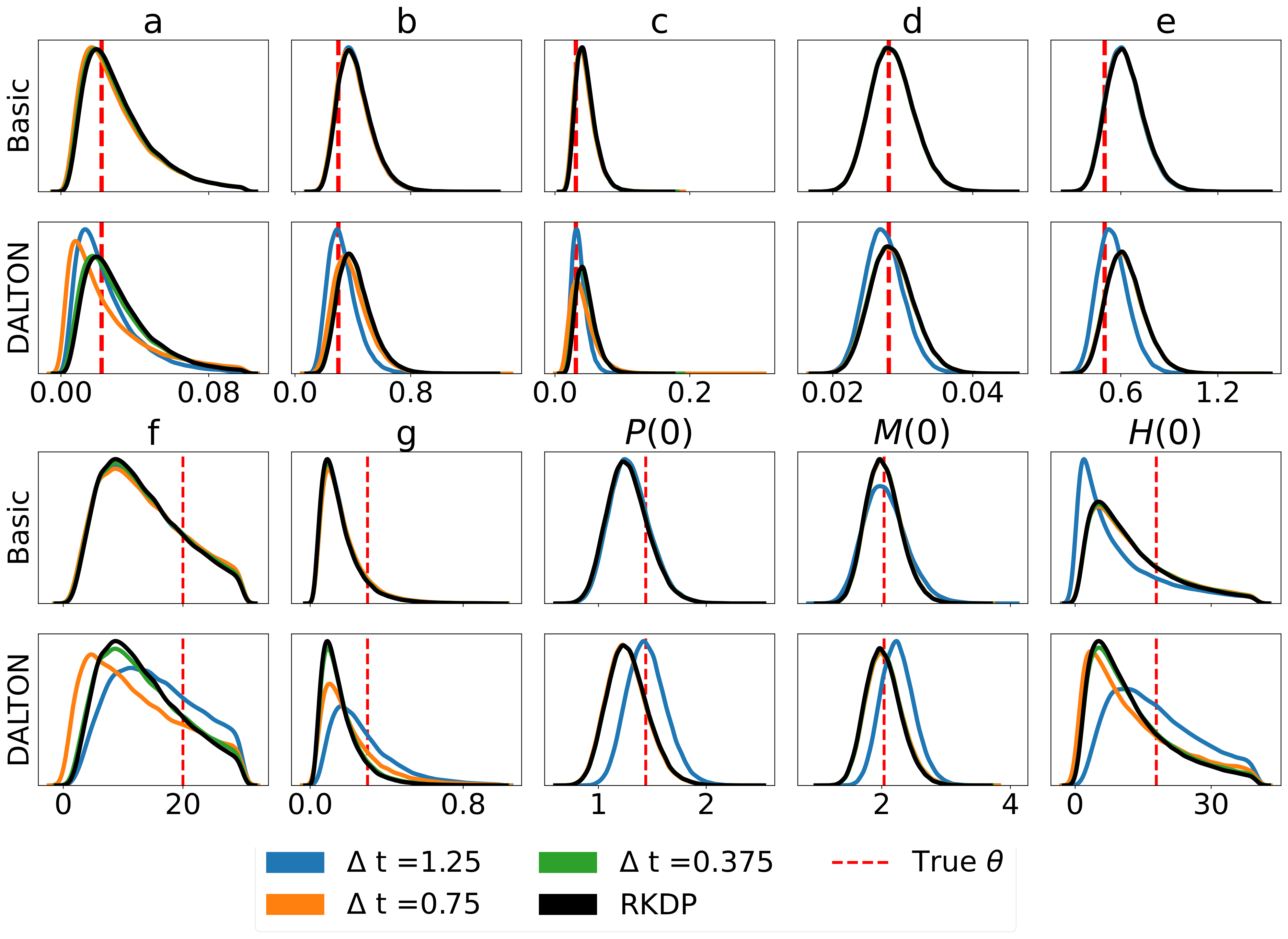
Berikut adalah beberapa hasil yang dihasilkan oleh berbagai perkiraan kemungkinan yang ditemukan di rodeo dari /examples/ :
Tes unit dapat dijalankan melalui perintah berikut:
cd tests
python -m unittest discover -v Atau, instal tox , lalu dari dalam rodeo masukkan baris perintah: tox .
Dokumentasi HTML dapat dikompilasi dari folder root:
pip install .[docs]
cd docs
make html Ini akan membuat dokumentasi di docs/build .