@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Tahukah Anda bahwa neurodiffeq mendukung kumpulan solusi dan dapat digunakan untuk menyelesaikan masalah sebaliknya? Lihat di sini!
? Sudah familiar dengan neurodiffeq? ? Langsung ke FAQ.
neurodiffeq adalah paket untuk menyelesaikan persamaan diferensial dengan jaringan saraf. Persamaan diferensial adalah persamaan yang menghubungkan suatu fungsi dengan turunannya. Mereka muncul dalam berbagai domain ilmiah dan teknik. Secara tradisional permasalahan ini dapat diselesaikan dengan metode numerik (misalnya beda hingga, elemen hingga). Meskipun metode ini efektif dan memadai, ekspresibilitasnya dibatasi oleh representasi fungsinya. Akan menarik jika kita dapat menghitung solusi persamaan diferensial yang kontinu dan terdiferensiasi.
Sebagai pendekatan fungsi universal, jaringan syaraf tiruan telah terbukti mempunyai potensi untuk memecahkan persamaan diferensial biasa (ODEs) dan persamaan diferensial parsial (PDEs) dengan kondisi awal/batas tertentu. Tujuan dari neurodiffeq adalah untuk mengimplementasikan teknik penggunaan ANN yang ada untuk menyelesaikan persamaan diferensial dengan cara yang memungkinkan perangkat lunak menjadi cukup fleksibel untuk menangani berbagai masalah yang ditentukan pengguna.
Seperti kebanyakan perpustakaan standar, neurodiffeq dihosting di PyPI. Untuk menginstal rilis stabil terbaru,
pip install -U neurodiffeq # '-U' berarti update ke versi terbaru
Alternatifnya, Anda dapat menginstal perpustakaan secara manual untuk mendapatkan akses awal ke fitur-fitur baru kami. Ini adalah cara yang direkomendasikan bagi pengembang yang ingin berkontribusi pada perpustakaan.
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip install -r persyaratan pemasangan pip. # Untuk membuat perubahan pada perpustakaan, gunakan `pip install -e .`pytest tes/ # Jalankan tes. Opsional.
Kami akan dengan senang hati membantu Anda jika ada pertanyaan. Sementara itu, Anda dapat membaca FAQ.
Untuk melihat tutorial lengkap dan dokumentasi neurodiffeq , silakan periksa Dokumentasi Resmi.
Selain dokumentasi, kami baru-baru ini membuat panduan singkat Video Demo dengan slide.
dari neurodiffeq impor difffrom neurodiffeq.solvers impor Solver1D, Solver2Ddari neurodiffeq.conditions impor IVP, DirichletBVP2Ddari neurodiffeq.networks impor FCNN, SinActv
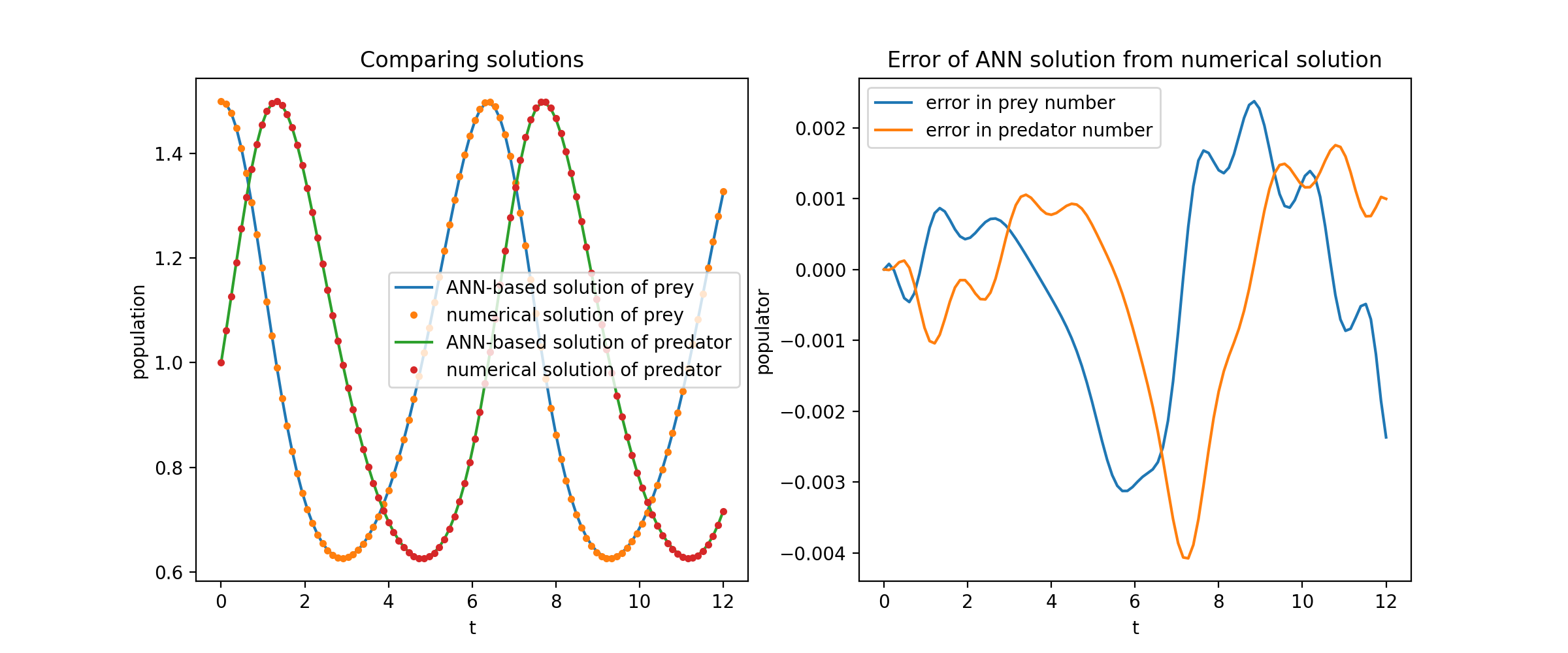
Di sini kita memecahkan sistem non-linier dari dua ODE, yang dikenal sebagai persamaan Lotka–Volterra. Ada dua fungsi yang tidak diketahui ( u dan v ) dan satu variabel independen ( t ).
def ode_system(u, v, t): mengembalikan [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]kondisi = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]jaring = [FCNN(actv=SinActv), FCNN(actv=SinActv)]pemecah = Solver1D(ode_system, kondisi, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution = solver.get_solution()
solution adalah objek yang dapat dipanggil, Anda dapat meneruskan array numpy atau tensor obor ke sana
u, v = solution(t, to_numpy=True) # t bisa berupa np.ndarray atau torch.Tensor
Merencanakan u dan v terhadap solusi analitiknya menghasilkan sesuatu seperti:
Di sini kita menyelesaikan Persamaan Laplace dengan kondisi batas Dirichlet pada sebuah persegi panjang. Perhatikan bahwa kami memilih persamaan Laplace karena kesederhanaannya dalam menghitung solusi analitis. Dalam praktiknya, Anda dapat mencoba PDE apa pun yang nonlinier dan kacau , asalkan Anda menyetel pemecahnya dengan cukup baik.
Menyelesaikan sistem PDE 2-D sangat mirip dengan menyelesaikan ODE, kecuali ada dua variabel x dan y untuk soal nilai batas atau x dan t untuk soal nilai batas awal, keduanya didukung.
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]kondisi = [DirichletBVP2D(x_min=0, x_min_val=lambda y: obor. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=lambda x: 0, y_max=1, y_max_val=lambda x: 0,
)
]jaring = [FCNN(n_input_units=2, n_output_units=1, unit_tersembunyi=(512,))]solver = Solver2D(pde_system, kondisi, xy_min=(0, 0), xy_max=(1, 1), jaring=jaring) solver.fit(max_epochs=2000)solusi = solver.get_solution() Tanda tangan solution untuk PDE 2D sedikit berbeda dari ODE. Sekali lagi, ini memerlukan array numpy atau tensor obor.
u = solusi(x, y, to_numpy=Benar)
Mengevaluasi u pada [0,1] × [0,1] menghasilkan plot berikut
| Solusi Berbasis ANN | Sisa PDE |
|---|---|
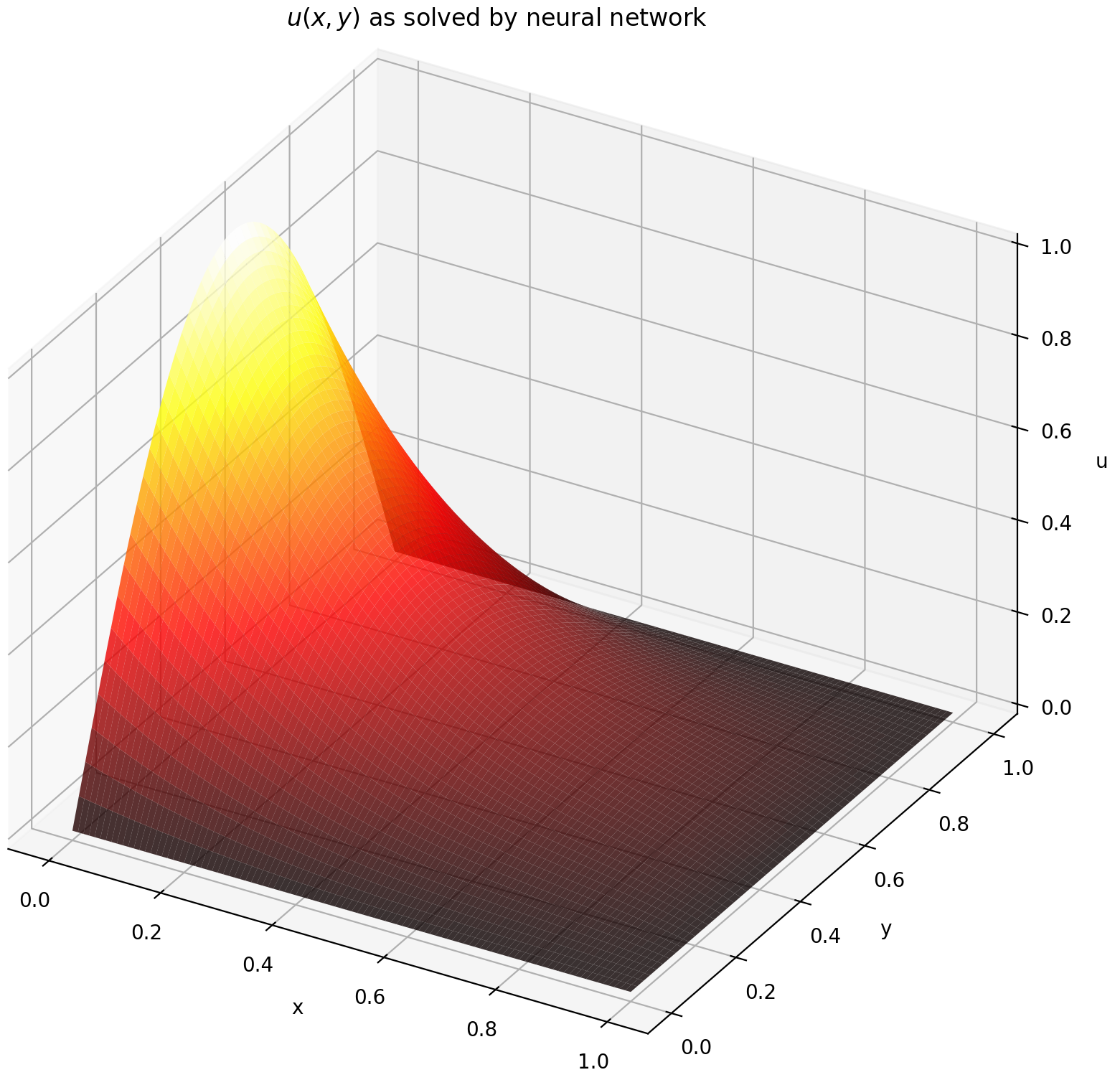 | 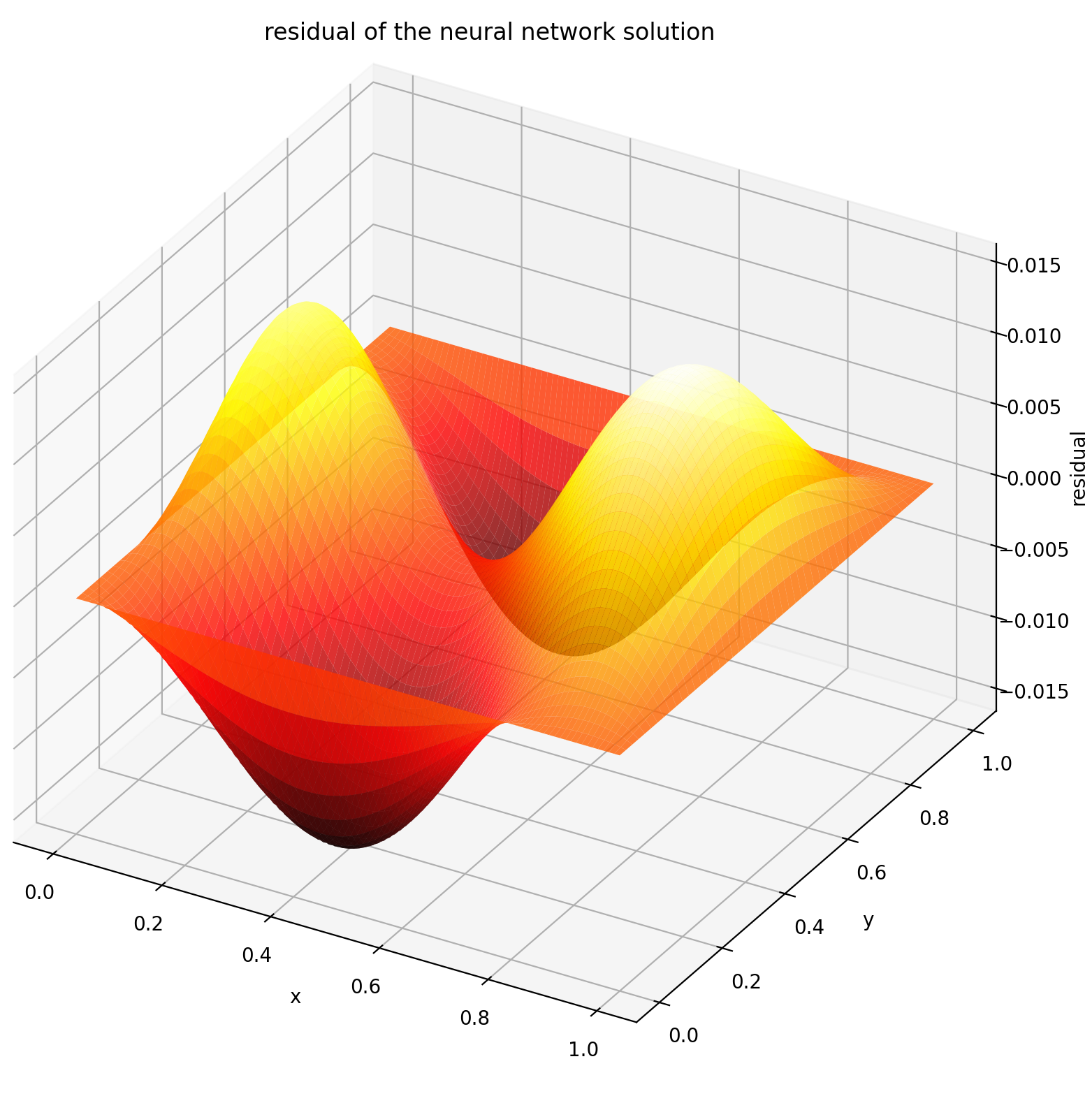 |
Monitor adalah alat untuk memvisualisasikan solusi PDE/ODE serta riwayat kerugian dan metrik khusus selama pelatihan. Pengguna Jupyter Notebooks perlu menjalankan keajaiban %matplotlib notebook . Untuk pengguna Jupyter Lab, coba %matplotlib widget .
dari neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
Anda akan melihat plot diperbarui setiap 100 epoch serta pada epoch terakhir , menampilkan dua plot — satu untuk visualisasi solusi pada interval [0,12] dan yang lainnya untuk riwayat kerugian (pelatihan dan validasi).
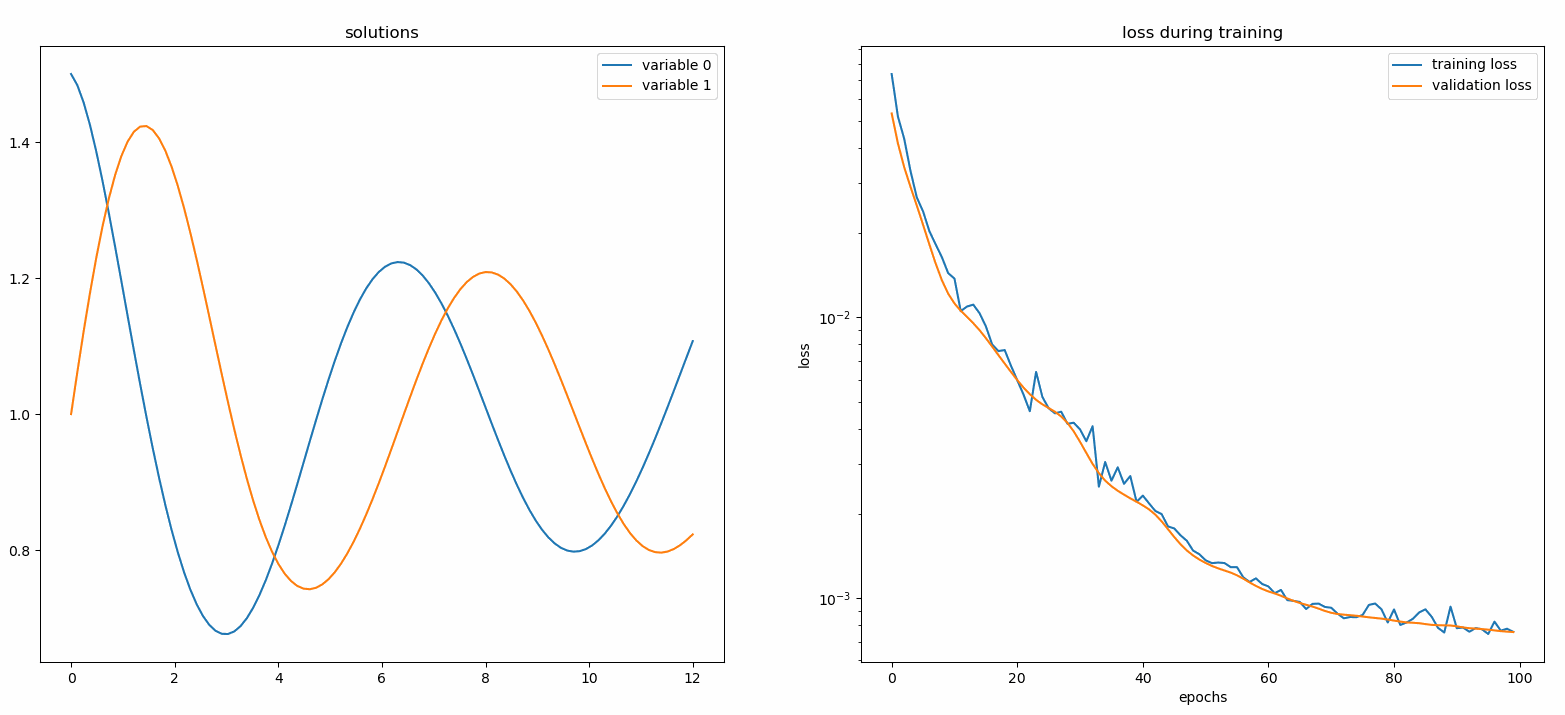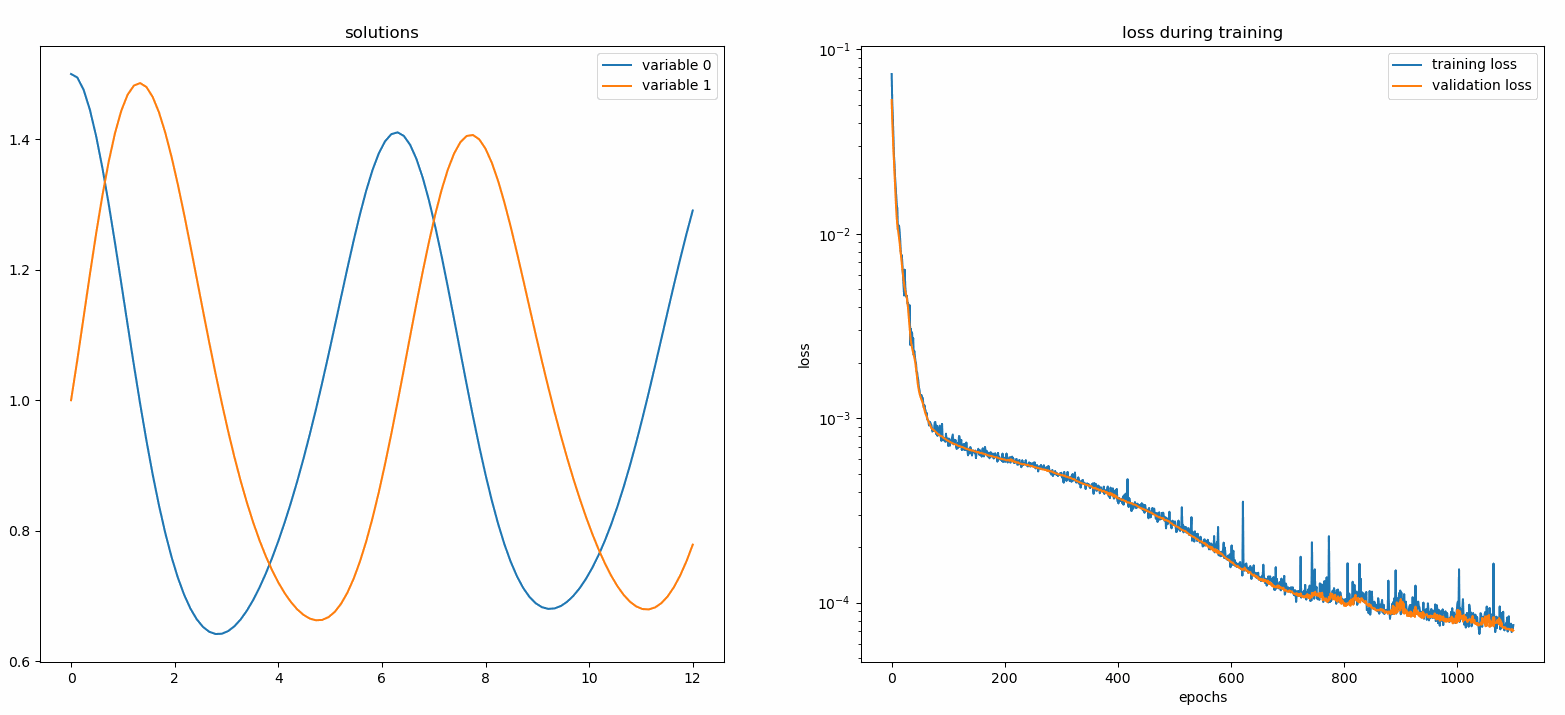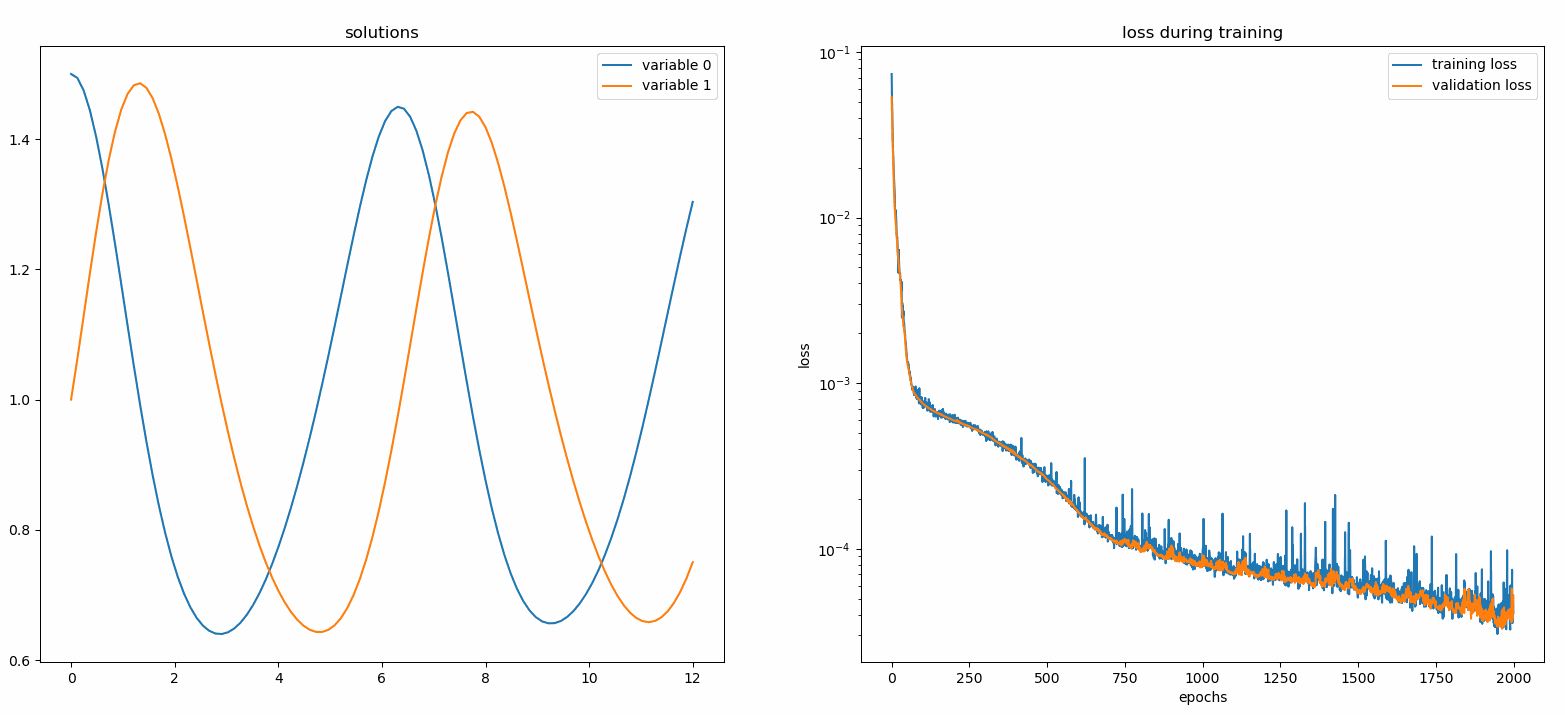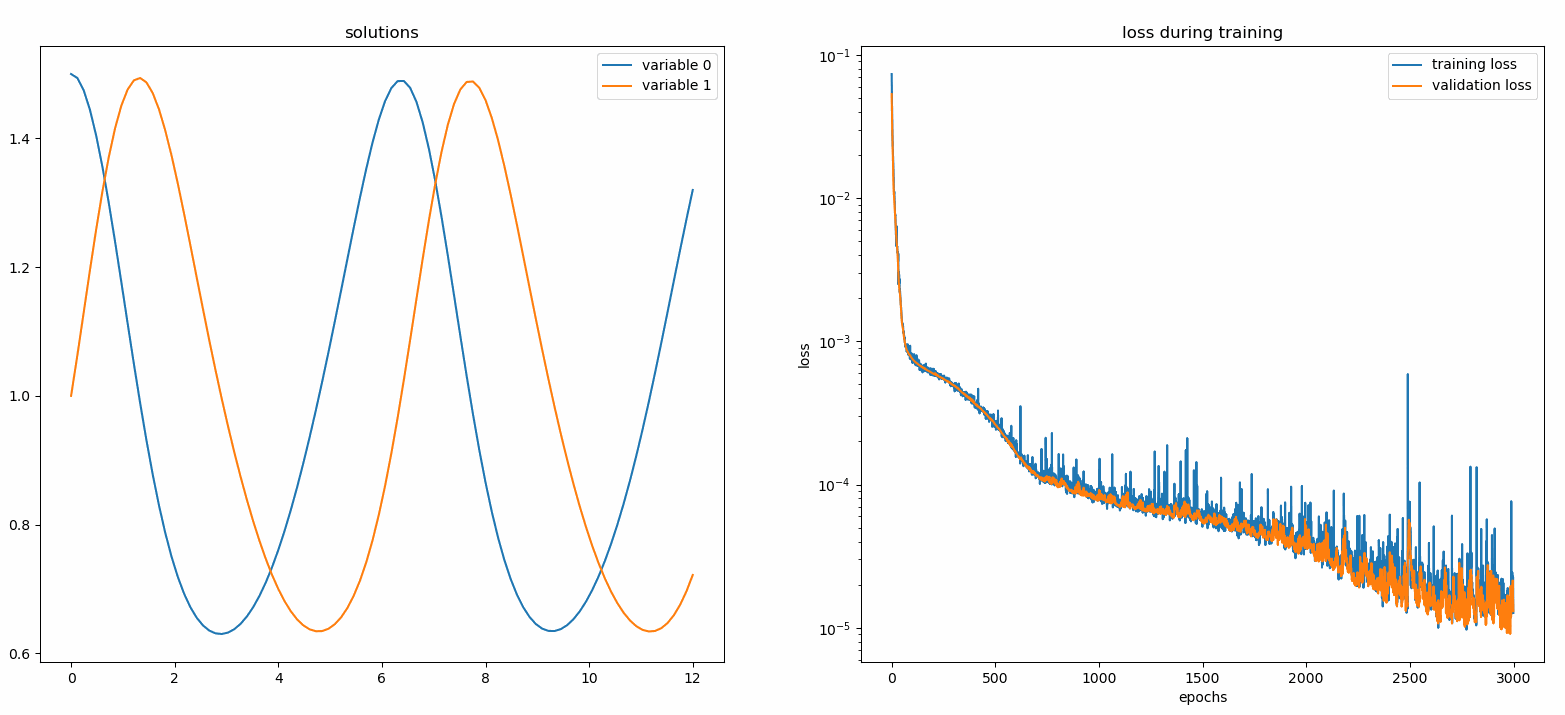
Demi kenyamanan, kami telah menerapkan FCNN – jaringan saraf yang terhubung sepenuhnya, yang unit tersembunyi dan fungsi aktivasinya dapat disesuaikan.
dari neurodiffeq.networks import FCNN# Default: n_input_units=1, n_output_units=1,hidden_units=[32, 32], activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=...,hidden_units=[ ..., ..., ...], aktivasi=...) ...jaring = [bersih1, bersih2, ...]
FCNN biasanya merupakan titik awal yang baik. Untuk pengguna tingkat lanjut, pemecah kompatibel dengan torch.nn.Module khusus apa pun. Satu-satunya kendala adalah:
Modul mengambil bentuk tensor (None, n_coords) dan menghasilkan output berbentuk tensor (None, 1) .
Harus ada total modul n_funcs di nets untuk diteruskan ke solver = Solver(..., nets=nets) .
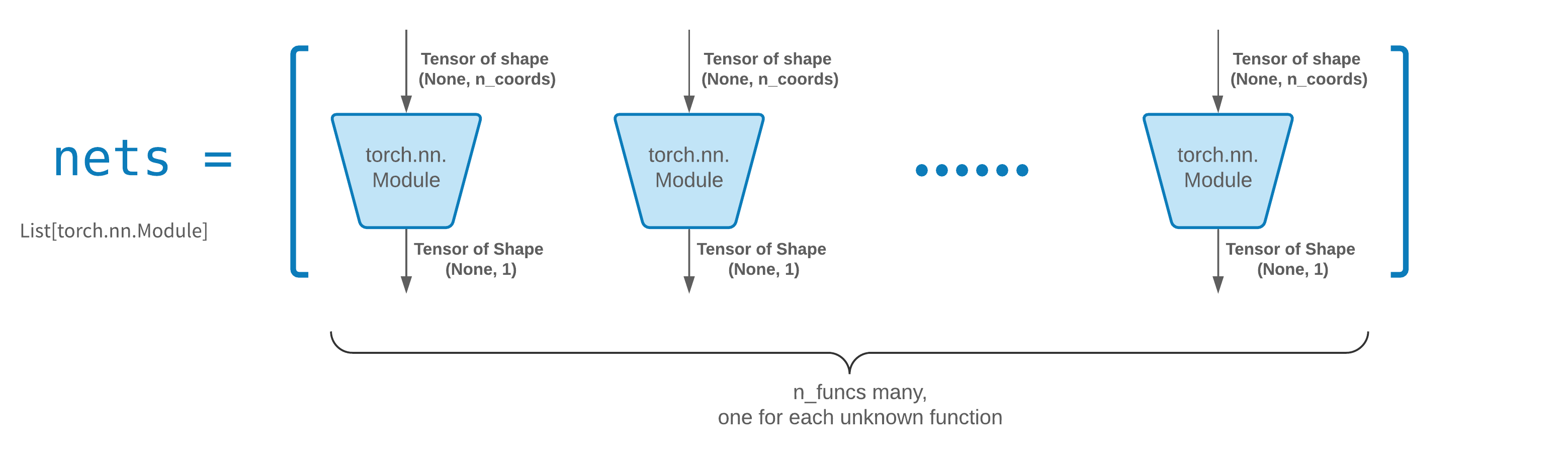
Sebenarnya, neurodiffeq memiliki fitur single_net yang tidak mematuhi aturan di atas, yang tidak akan dibahas di sini.
Baca tutorial PyTorch tentang membangun arsitektur jaringan Anda sendiri (alias modul).
Pembelajaran transfer mudah dilakukan dengan membuat serial old_solver.nets (daftar modul obor) ke disk dan kemudian memuatnya dan meneruskannya ke solver baru:
old_solver.fit(max_epochs=...)# ... membuang `old_solver.nets` ke disk# ... memuat jaringan dari disk, menyimpannya di beberapa `loaded_nets` variabelnew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
Saat ini kami sedang mengerjakan fungsi wrapper untuk menyimpan/memuat jaringan dan variabel internal Solvers lainnya. Sementara itu, Anda dapat membaca tutorial PyTorch tentang menyimpan dan memuat jaringan Anda.
Dalam neurodiffeq, jaringan dilatih dengan meminimalkan kerugian (residu ODE/PDE) yang dievaluasi pada sekumpulan titik dalam domain. Poin-poin tersebut diambil sampelnya secara acak setiap saat. Untuk mengontrol jumlah, distribusi, dan domain pembatas titik sampel, Anda dapat menentukan generator pelatihan/validasi Anda sendiri.
dari neurodiffeq.generators import Generator1D# Default t_min=0.0, t_max=1.0, method='uniform', noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., noise_std=...)g2 = Generator1D(ukuran=..., t_min=..., t_max=..., metode=..., noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
Berikut adalah beberapa contoh distribusi Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
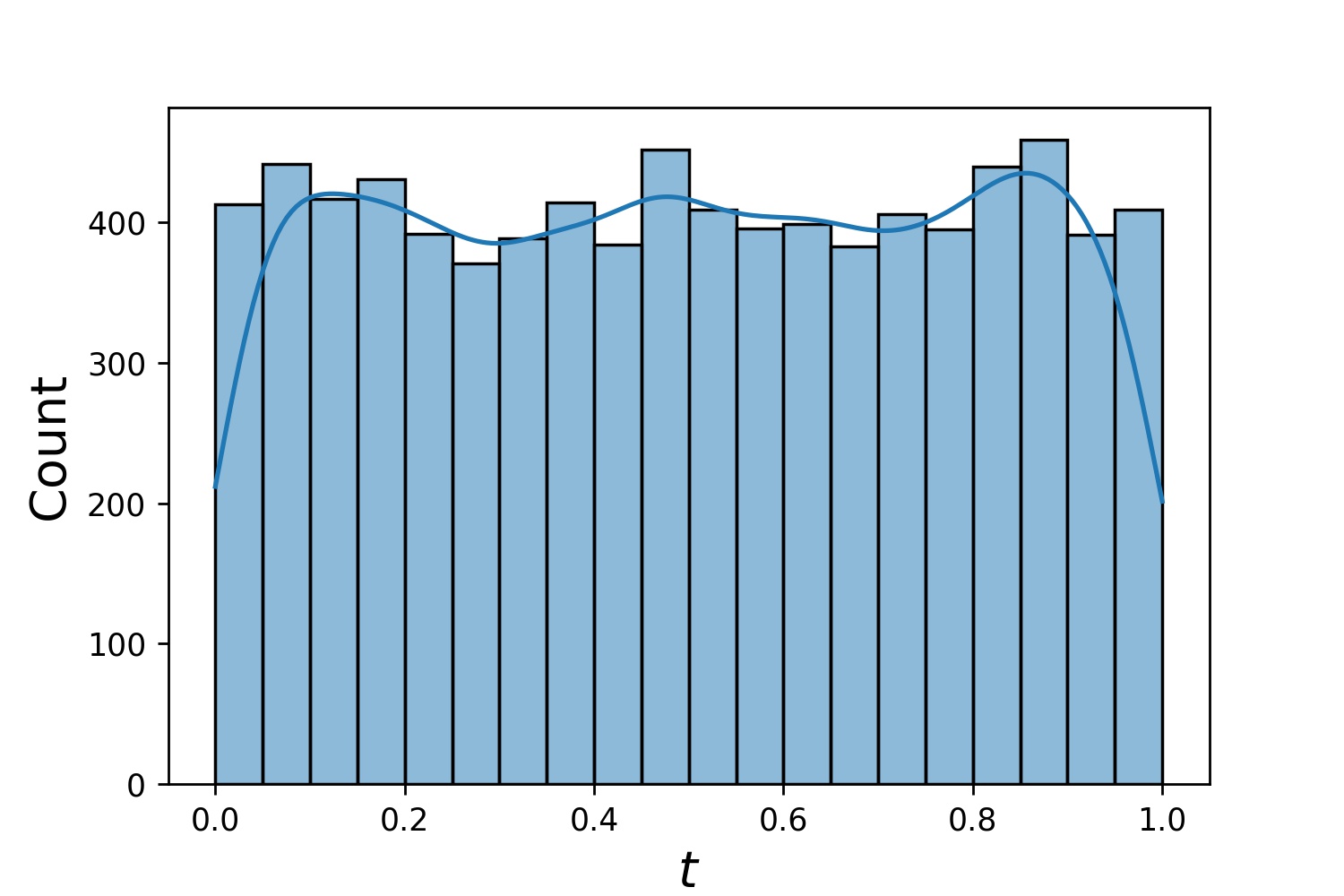 | 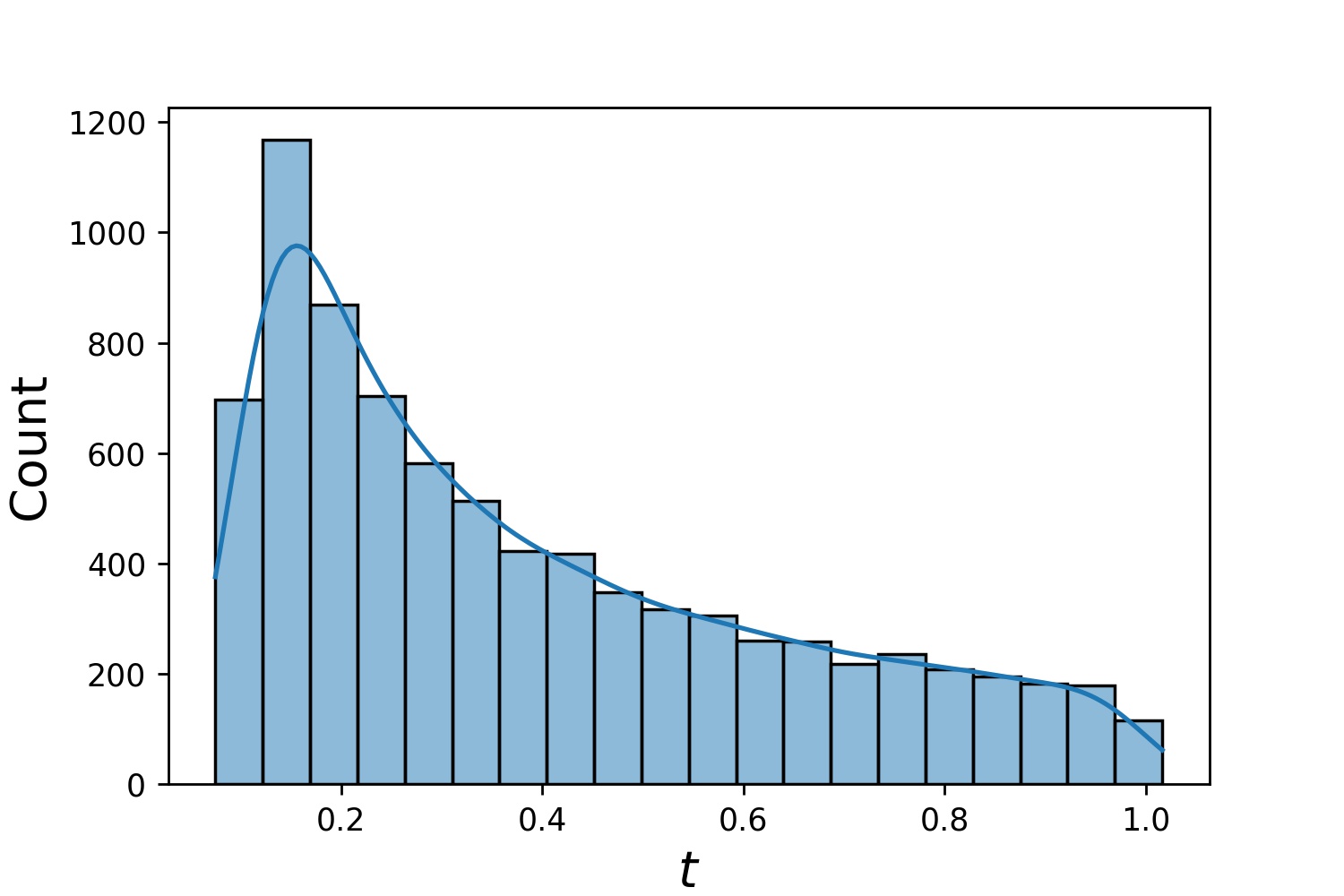 |
Perhatikan bahwa ketika train_generator dan valid_generator ditentukan, t_min dan t_max dapat dihilangkan di Solver1D(...) . Faktanya, meskipun Anda meneruskan t_min , t_max , train_generator , valid_generator secara bersamaan, t_min dan t_max akan tetap diabaikan.
Fitur bagus lainnya dari generator ini adalah Anda dapat menggabungkannya, misalnya
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2
Di sini, g akan menjadi generator yang mengeluarkan sampel gabungan g1 dan g2
g1 | g2 | g1 + g2 |
|---|---|---|
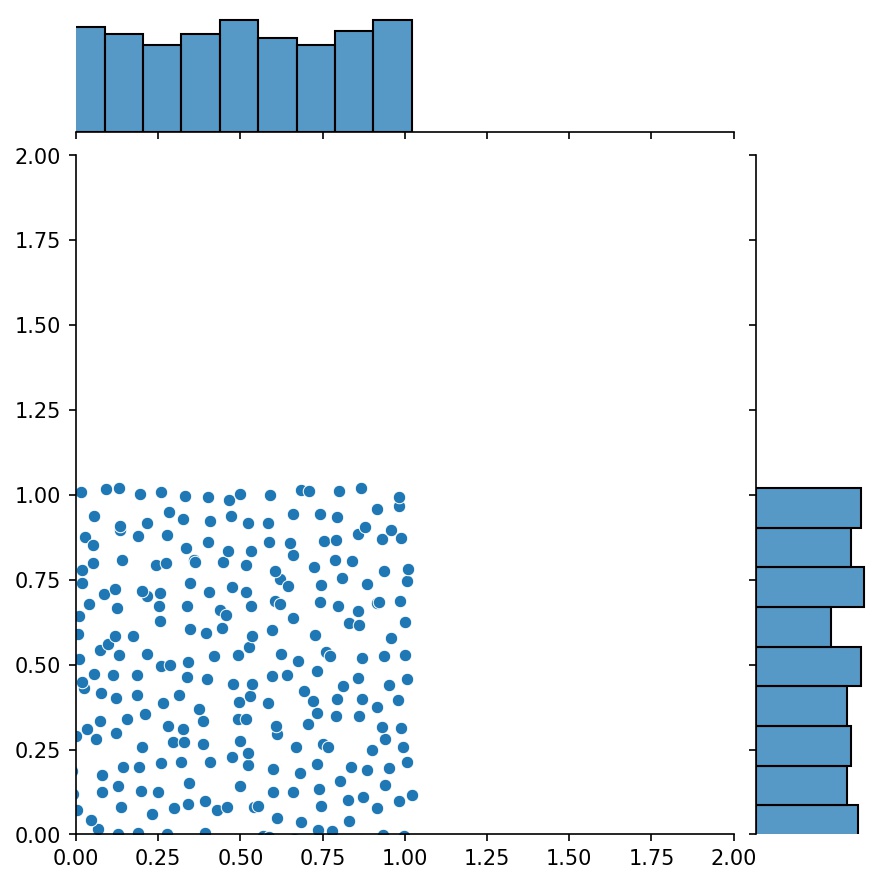 | 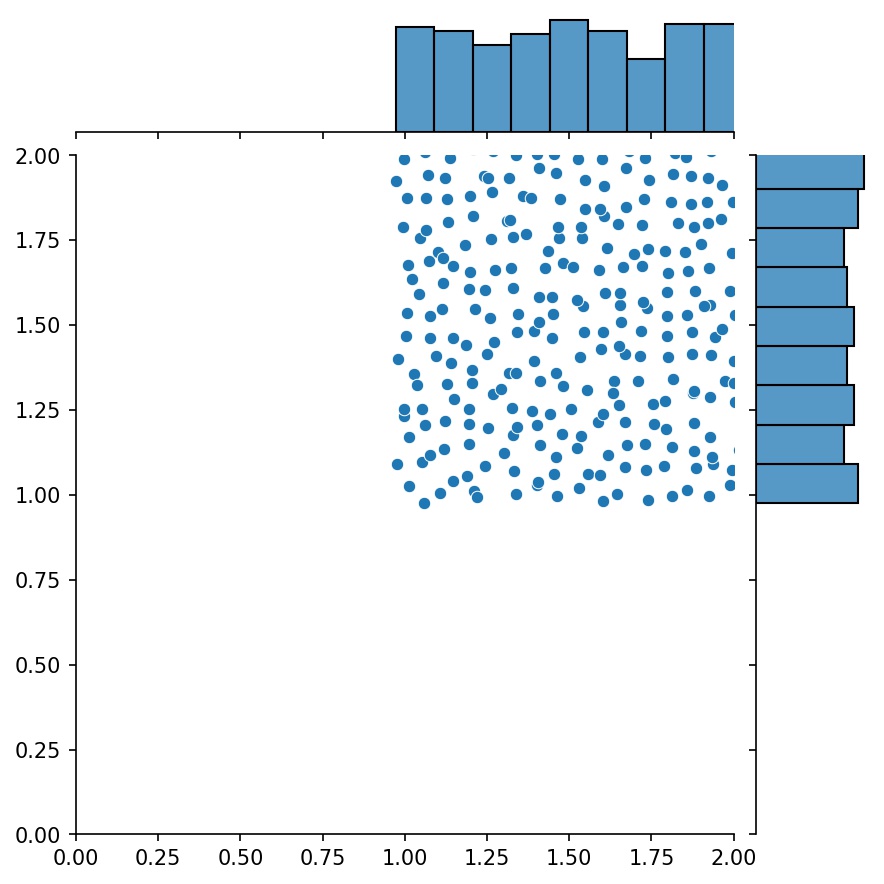 | 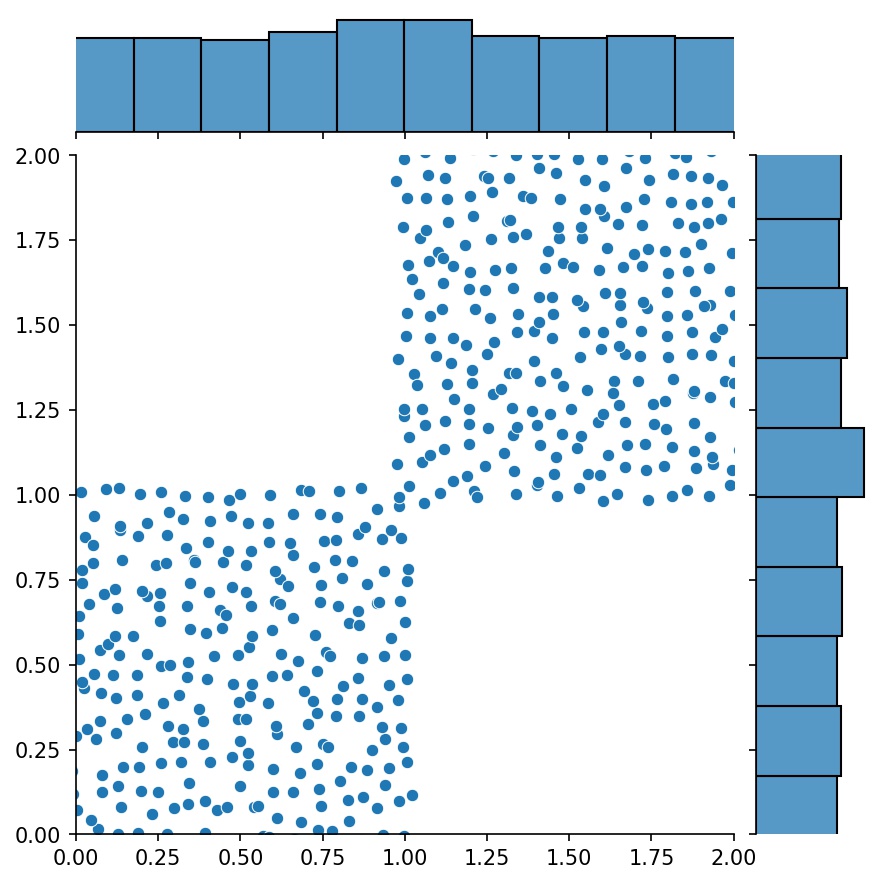 |
Anda dapat menggunakan Generator2D , Generator3D , dll. untuk titik pengambilan sampel dalam dimensi yang lebih tinggi. Tapi ada juga cara lain
g1 = Generator1D(1024, 2.0, 3.0, metode='seragam')g2 = Generator1D(1024, 0.1, 1.0, metode='log-spasi-noisy', noise_std=0.001)g = g1 * g2
Di sini, g akan menjadi generator yang menghasilkan 1024 titik dalam persegi panjang 2-D (2,3) × (0.1,1) setiap saat. Koordinat x diambil dari (2,3) menggunakan strategi uniform dan koordinat y diambil dari (0.1,1) menggunakan strategi log-spaced-noisy .
g1 | g2 | g1 * g2 |
|---|---|---|
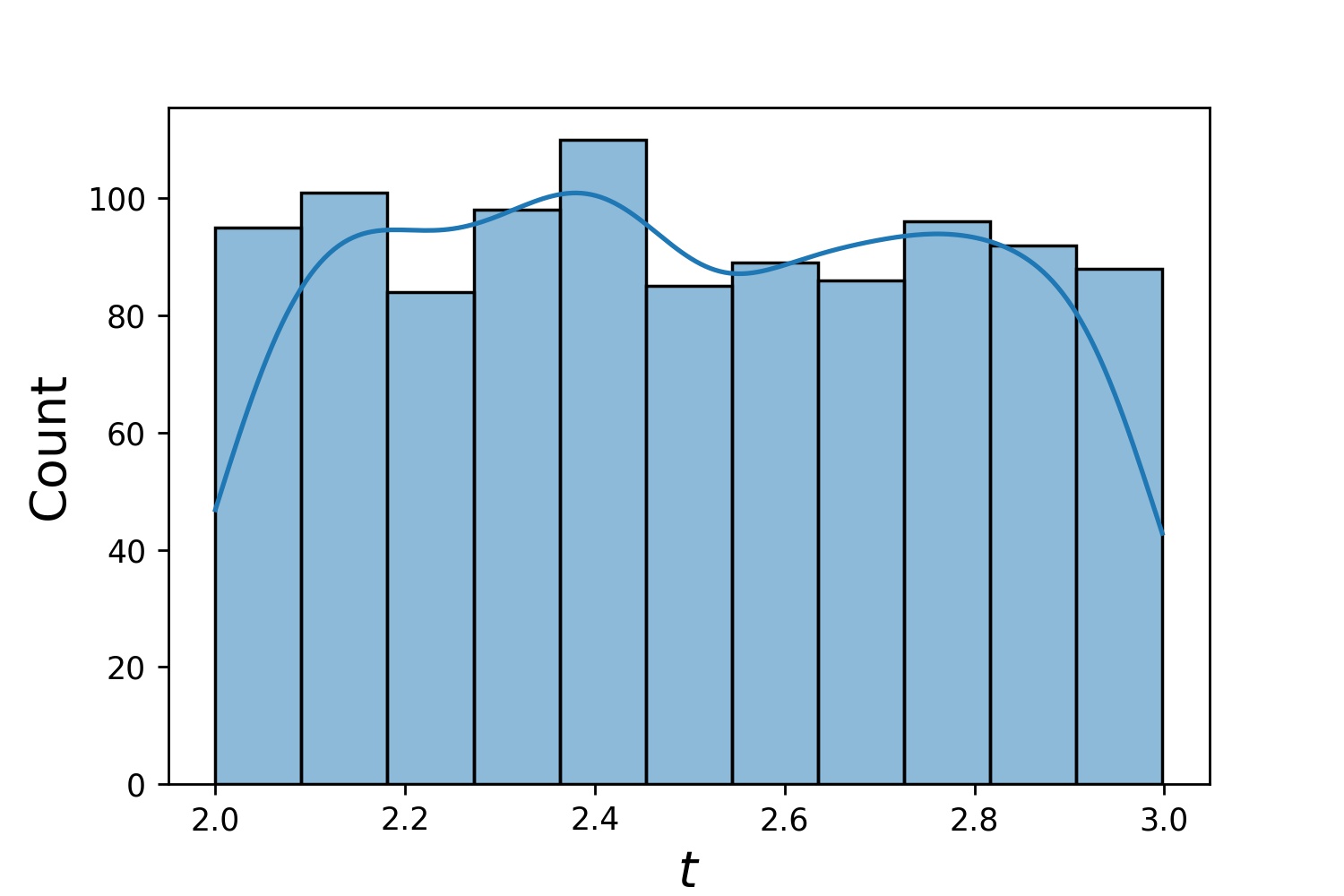 | 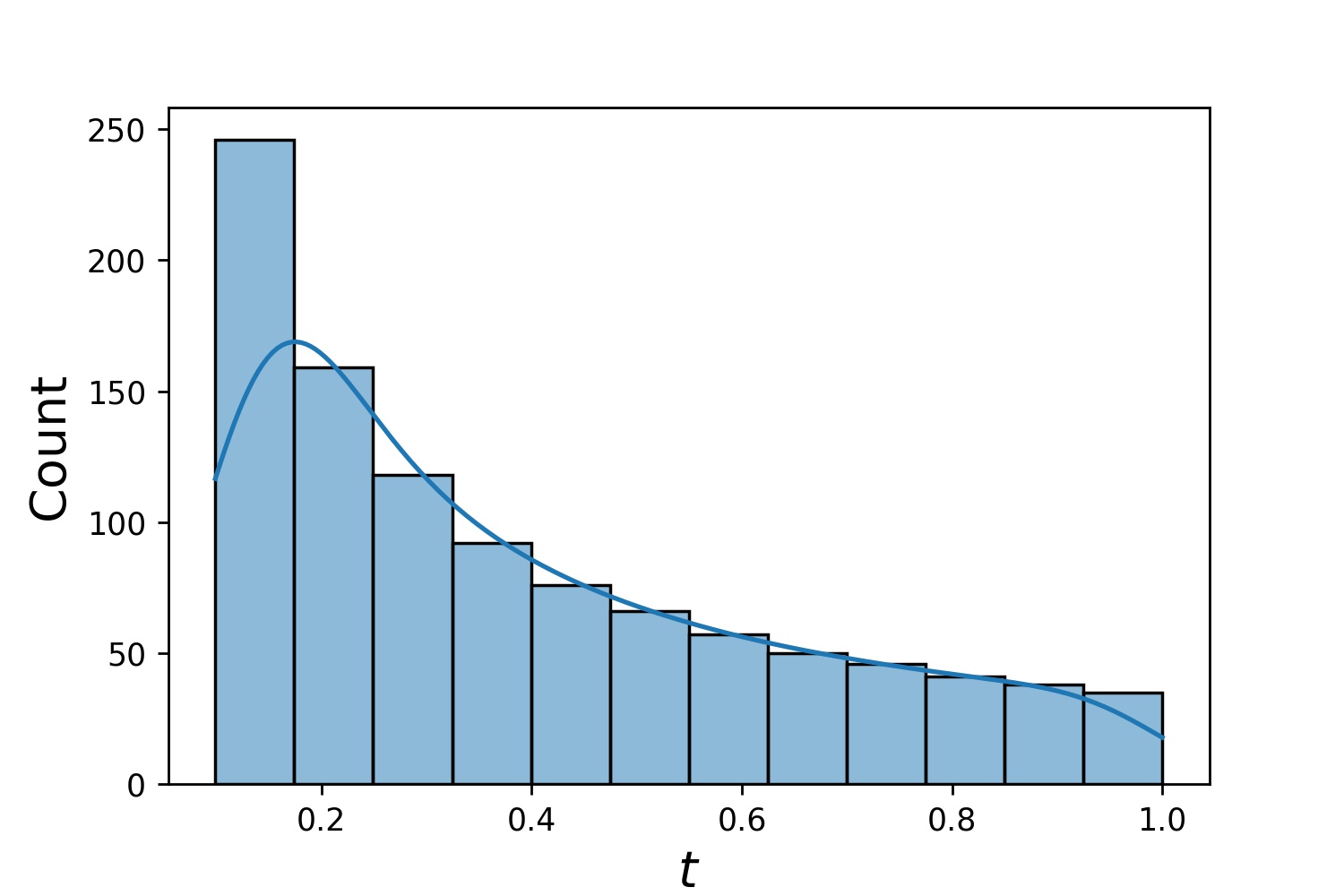 | 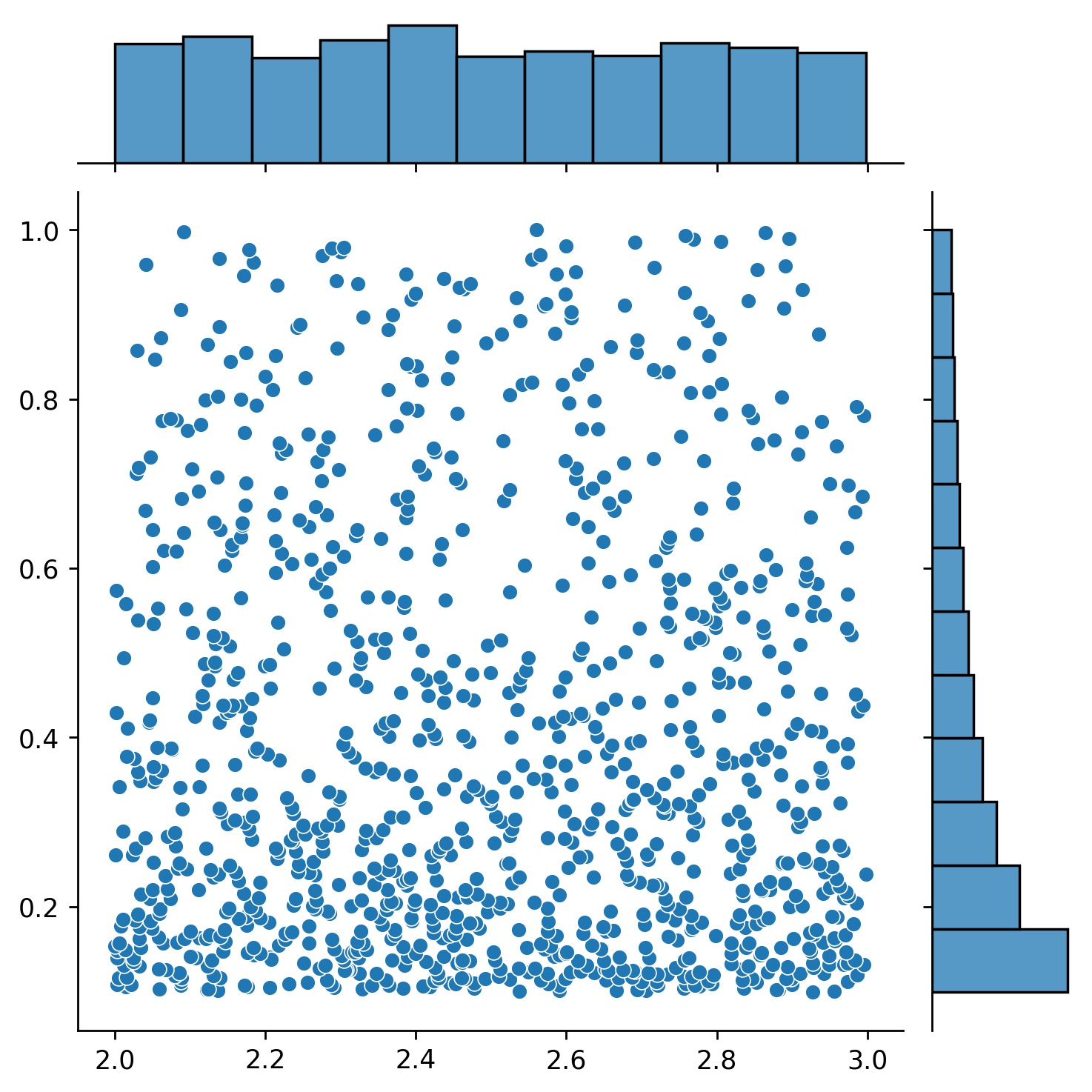 |
Terkadang, menarik untuk menyelesaikan sekumpulan persamaan sekaligus. Misalnya, Anda mungkin ingin menyelesaikan persamaan diferensial dalam bentuk du/dt + λu = 0 pada kondisi awal u(0) = U0 . Anda mungkin ingin menyelesaikan masalah ini untuk semua λ dan U0 sekaligus, dengan memperlakukannya sebagai masukan ke jaringan saraf.
Salah satu penerapannya adalah untuk reaksi kimia, yang laju reaksinya tidak diketahui. Laju reaksi yang berbeda berhubungan dengan solusi yang berbeda, dan hanya satu solusi yang cocok dengan titik data yang diamati. Anda mungkin tertarik untuk menyelesaikan sekumpulan solusi terlebih dahulu, lalu menentukan laju reaksi terbaik (alias parameter persamaan). Langkah kedua dikenal sebagai masalah invers .
Berikut ini contoh cara melakukan ini menggunakan neurodiffeq :
Katakanlah kita mempunyai persamaan du/dt + λu = 0 dan kondisi awal u(0) = U0 dimana λ dan U0 adalah konstanta yang tidak diketahui. Kami juga memiliki serangkaian observasi t_obs dan u_obs . Kami terlebih dahulu mengimpor BundleSolver dan BundleIVP yang diperlukan untuk mendapatkan paket solusi:
dari neurodiffeq.conditions import BundleIVPfrom neurodiffeq.solvers import BundleSolver1Dimport matplotlib.pyplot as pltimport numpy as npimport torchfrom neurodiffeq import diff
Kami menentukan domain masukan t , serta domain parameter λ dan U0 . Kita juga perlu membuat keputusan tentang urutan parameternya. Yakni, mana yang harus menjadi parameter pertama, dan mana yang harus menjadi parameter kedua. Untuk tujuan demo ini, kami memilih λ sebagai parameter pertama (indeks 0), dan U0 sebagai parameter kedua (indeks 1). Sangat penting untuk melacak indeks parameter.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5# parameter pertama, indeks = 0U0_MIN, U0_MAX = 0.2, 0.6# parameter kedua, indeks = 1
Kami kemudian mendefinisikan conditions dan solver seperti biasa, kecuali kami menggunakan BundleIVP dan BundleSolver1D bukan IVP dan Solver1D . Antarmuka keduanya sangat mirip dengan IVP dan Solver1D . Anda dapat mengetahui lebih lanjut di referensi API.
# parameter persamaan muncul setelah input (biasanya koordinat temporal dan spasial)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# Argumen kata kunci harus diberi nama "u_0" di BundleIVP. Jika Anda menggunakan yang lain, misalnya `y0`, `u0`, dll., itu tidak akan berfungsi.conditions = [BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 has indeks 1]solver = BundleSolver1D(ode_system=diff_eq,kondisi=kondisi,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ memiliki indeks 0; u_0 memiliki indeks 1theta_max=[LAMBDA_MAX, U0_MAX], # λ memiliki indeks 0; parameter persamaan, yang memiliki indeks 0n_batches_valid=1,
) Karena λ adalah parameter dalam persamaan dan U0 adalah parameter pada kondisi awal , maka kita harus memasukkan λ pada diff_eq dan U0 pada kondisi tersebut. Jika suatu parameter ada dalam persamaan dan kondisi, maka parameter tersebut harus dimasukkan di kedua tempat. Semua elemen conditions yang diteruskan ke BundleSovler1D harus berupa kondisi Bundle* , meskipun elemen tersebut tidak memiliki parameter.
Sekarang, kita bisa melatihnya dan mendapatkan solusinya seperti biasa.
solver.fit(max_epochs=1000)solusi = solver.get_solution(best=True)
Solusinya mengharapkan tiga masukan - t , λ dan U0 . Semua masukan harus memiliki bentuk yang sama. Misalnya, jika Anda tertarik untuk memperbaiki λ=4 dan U0=0.4 dan memplot solusi u terhadap t ∈ [0,1] , Anda dapat melakukan hal berikut
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0,4 * np.ones_like(t)u = solution(t, lmd, u0, to_numpy=True)import matplotlib.pyplot sebagai pltplt .plot(t, kamu)
Setelah Anda memiliki solution gabungan, Anda dapat menemukan sekumpulan parameter (λ, U0) yang paling cocok dengan titik data pengamatan (t_i, u_i) . Hal ini dicapai dengan menggunakan penurunan gradien sederhana. Dalam contoh mainan berikut, kita asumsikan hanya ada tiga titik data u(0.2) = 0.273 , u(0.5)=0.129 , dan u(0.8) = 0.0609 . Berikut ini adalah alur kerja PyTorch klasik.
# data yang diamati pointst_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# inisialisasi acak dari λ dan U0; melacak gradiennyalmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)# menjalankan penurunan gradien selama 10.000 epoch selama _ dalam rentang(10000):output = solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs ))kerugian = ((keluaran - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, rugi = {loss.item()}") Sederhana. Saat mengimpor neurodiffeq, perpustakaan secara otomatis mendeteksi apakah CUDA tersedia di mesin Anda. Karena perpustakaan didasarkan pada PyTorch, perpustakaan akan menetapkan jenis tensor default ke torch.cuda.DoubleTensor jika perangkat GPU yang kompatibel ditemukan.
Lihat Bagian Jaringan Kustom dan Pembelajaran Transfer.
Cara standar PyTorch.
Bangun jaringan Anda seperti yang dijelaskan dalam Jaringan Khusus: nets = [FCNN(), FCN(), ...]
Buat instance pengoptimal khusus dan teruskan semua parameter jaringan ini ke pengoptimal tersebut
parameter = [p untuk net di net untuk p di net.parameters()] # daftar parameter semua jaringanMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameter, lr=MY_LEARNING_RATE, ...)
Berikan KEDUA nets dan optimizer Anda ke pemecah: solver = Solver1D(..., nets=nets, optimizer=optimizer)
Tidak seperti metode numerik tradisional (FEM, FVM, dll.), solusi berbasis NN memerlukan beberapa penyesuaian. Pustaka menawarkan fleksibilitas maksimal untuk mencoba kombinasi hyperparameter apa pun.
Untuk menggunakan arsitektur jaringan yang berbeda, Anda dapat meneruskan torch.nn.Module khusus Anda.
Untuk menggunakan pengoptimal yang berbeda, Anda dapat meneruskan pengoptimal Anda sendiri ke solver = Solver(..., optimizer=my_optim) .
Untuk menggunakan distribusi pengambilan sampel yang berbeda, Anda dapat menggunakan generator bawaan atau menulis generator Anda sendiri dari awal.
Untuk menggunakan ukuran pengambilan sampel yang berbeda, Anda dapat mengubah generator atau mengubah solver = Solver(..., n_batches_train) .
Untuk mengubah hyperparameter secara dinamis selama pelatihan, periksa fitur panggilan balik kami.
Jangan gunakan ReLU untuk aktivasi, karena turunan orde keduanya identik dengan 0.
Skala ulang PDE/ODE Anda dalam bentuk tak berdimensi, sebaiknya buat semuanya berkisar dalam [0,1] . Bekerja dengan domain seperti [0,1000000] rentan terhadap kegagalan karena a) PyTorch menginisialisasi bobot modul menjadi relatif kecil dan b) sebagian besar fungsi aktivasi (seperti Sigmoid, Tanh, Swish) paling nonlinier mendekati 0.
Jika PDE/ODE Anda terlalu rumit, pertimbangkan untuk mencoba pembelajaran kurikulum. Mulailah melatih jaringan Anda pada domain yang lebih kecil, lalu kembangkan secara bertahap hingga seluruh domain tercakup.
Setiap orang dipersilakan untuk berkontribusi pada proyek ini.
Saat berkontribusi pada repositori ini, kami mempertimbangkan proses berikut:
Buka terbitan untuk mendiskusikan perubahan yang Anda rencanakan.
Pelajari Pedoman Kontribusi.
Lakukan perubahan pada repositori bercabang dan perbarui README.md jika ada perubahan pada antarmuka.
Buka permintaan tarik.