Implementasi Algoritma Minimax AI pada game Tic-Tac-Toe (atau Noughts and Crosses). Cobalah: Tic-tac-toe - Minimax
Untuk menyelesaikan permainan menggunakan AI, kami akan memperkenalkan konsep pohon permainan yang diikuti dengan algoritma minimax. Berbagai keadaan permainan diwakili oleh simpul-simpul di pohon permainan, sangat mirip dengan masalah perencanaan di atas. Idenya hanya sedikit berbeda. Dalam pohon permainan, simpul-simpul disusun dalam tingkatan yang sesuai dengan giliran masing-masing pemain dalam permainan sehingga simpul “akar” pohon (biasanya digambarkan di bagian atas diagram) adalah posisi awal dalam permainan. Dalam tic-tac-toe, ini akan menjadi grid kosong tanpa X atau Os yang dimainkan. Di bawah root, pada level kedua, terdapat kemungkinan keadaan yang dapat dihasilkan dari pergerakan pemain pertama, baik itu X atau O. Kita menyebut node ini sebagai “anak” dari node root.
Setiap node pada level kedua, selanjutnya akan memiliki node anak-anak yang dapat dicapai darinya melalui gerakan pemain lawan. Ini dilanjutkan, level demi level, hingga mencapai kondisi di mana permainan berakhir. Dalam tic-tac-toe, ini berarti salah satu pemain mendapatkan tiga baris dan menang, atau papan penuh dan permainan berakhir seri.
Minimax adalah kecerdasan buatan yang diterapkan dalam permainan dua pemain, seperti tic-tac-toe, checker, catur, dan go. Permainan ini disebut permainan zero-sum, karena secara matematis: satu pemain menang (+1) dan pemain lainnya kalah (-1) atau keduanya tidak menang (0).
Algoritme mencari, secara rekursif, langkah terbaik yang mengarahkan pemain Max menang atau tidak kalah (seri). Ia mempertimbangkan keadaan permainan saat ini dan gerakan yang tersedia pada keadaan tersebut, kemudian untuk setiap gerakan yang valid ia bermain (bergantian min dan max ) hingga menemukan keadaan terminal (menang, seri atau kalah).
Algoritma dipelajari oleh buku Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009). Kodesemu (diadaptasi):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Sekarang kita akan melihat setiap bagian dari pseudocode ini dengan implementasi Python. Implementasi Python tersedia di repositori ini. Pertama-tama, pertimbangkan ini:
papan = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
MAKS = +1
menit = -1
MAXnya mungkin X atau O dan MINnya mungkin O atau X, terserah. Papannya berukuran 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Kedua pemain memulai dengan skor terburuk Anda. Jika pemainnya MAX, skornya adalah -infinity. Jika tidak, jika pemainnya MIN, skornya adalah +tak terhingga. Catatan: infinity adalah alias untuk inf (dari modul matematika, dengan Python).
Langkah terbaik di papan adalah [-1, -1] (baris dan kolom) untuk semuanya.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreJika kedalamannya sama dengan nol, maka papan tidak memiliki sel kosong baru untuk dimainkan. Atau, jika seorang pemain menang, maka permainan berakhir MAX atau MIN. Jadi skor untuk negara bagian itu akan dikembalikan.
Sekarang kita akan melihat bagian utama dari kode ini yang berisi rekursi.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yUntuk setiap gerakan yang valid (sel kosong):
Pergerakan (+1 atau -1) di papan dibatalkan dan baris, kolom dikumpulkan.
Langkah selanjutnya adalah membandingkan skor dengan yang terbaik.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreUntuk pemain MAX, skor yang lebih besar akan diterima. Untuk pemain MIN, skor yang lebih rendah akan diterima. Dan pada akhirnya, langkah terbaiknya dikembalikan. Algoritma terakhir:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best Di bawah, langkah terbaik ada di tengah karena nilai maksimalnya ada di node ke-2 di sebelah kiri.
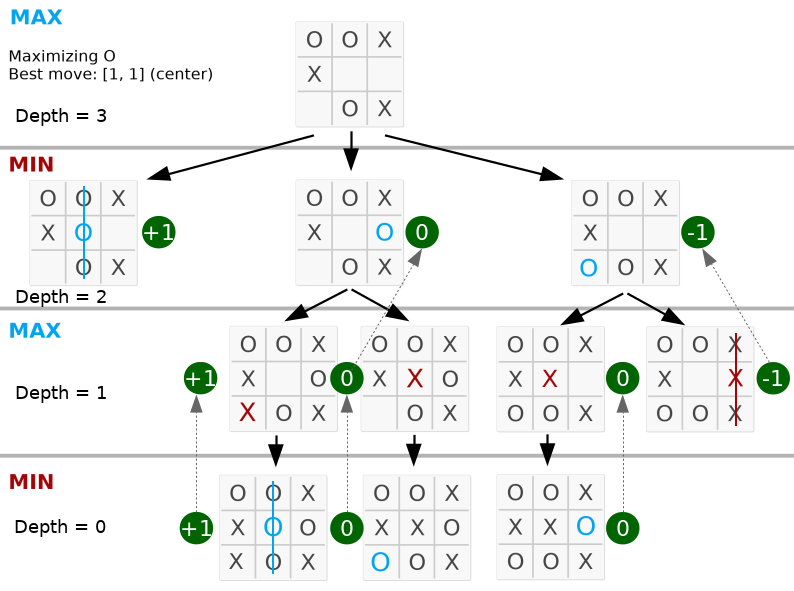
Perhatikan bahwa kedalamannya sama dengan gerakan valid di papan. Kode lengkap tersedia di py_version/ .
Pohon permainan yang disederhanakan:
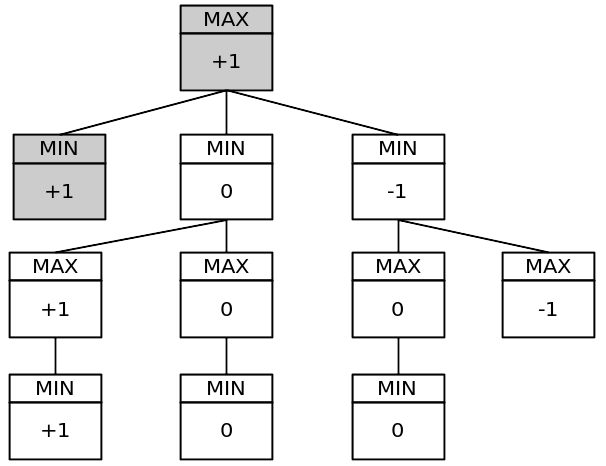
Pohon itu memiliki 11 node. Pohon permainan lengkap memiliki 549.946 node! Anda dapat mengujinya dengan memasukkan variabel global statis ke dalam program Anda dan menambahkannya untuk setiap pemanggilan fungsi minimax per giliran.
Dalam permainan yang lebih kompleks, seperti catur, sulit untuk mencari pohon permainan secara keseluruhan. Namun, Pemangkasan Alfa-beta merupakan metode optimasi pada algoritma minimax yang memungkinkan kita mengabaikan beberapa cabang pada pohon pencarian, karena ia memotong node (subpohon) yang tidak relevan dalam pencarian. Untuk informasi lebih lanjut, lihat: