
dan tugas Fiber di React, dan tugas Fiber yang berbeda memiliki prioritas yang berbeda pula. React perlu memproses tugas dengan prioritas tinggi terlebih dahulu. Misalnya, klik dan masukan pengguna adalah tugas dengan prioritas tinggi, karena operasi pengguna pasti diharapkan memiliki efek langsung, sehingga dapat meningkatkan pengalaman pengguna. Misalnya, prioritas acara animasi harus lebih rendah. Setelah tugas baru dengan prioritas tinggi memasuki antrian, React perlu memprosesnya terlebih dahulu.
Untuk menyimpan tugas-tugas ini, ada dua kumpulan tugas di React.
// Tugas disimpan di tumpukan minimum var taskQueue = []; var timerQueue = [];
taskQueue dan timerQueue keduanya merupakan array. Array pertama menyimpan tugas yang harus segera dieksekusi, sedangkan array kedua menyimpan tugas yang dapat ditunda.
var Tugas baru = {
id: taskIdCounter++, // Tandai id tugas
panggilan balik, // tingkat prioritas fungsi panggilan balik, // Waktu mulai prioritas tugas, // waktu mulai tugas, waktu kedaluwarsa titik waktu, // waktu kedaluwarsa, indeks pengurutan titik waktu: -1, // pengurutan tugas, nilainya berasal dari waktu kedaluwarsa, jadi nilainya Semakin kecil nilainya, semakin tinggi prioritasnya}; Setelah tugas baru masuk ke React, ia akan menggunakan CurrentTime terlebih dahulu untuk mencatat waktu saat ini (kinerja.sekarang() atau Tanggal.sekarang()). parameter penundaan, maka tugas memulai waktu eksekusi = waktu saat ini + penundaan;. Selanjutnya jika startTime > currentTime ditetapkan, itu membuktikan bahwa tugas dapat ditunda, kemudian tugas masuk ke timerQueue, jika tidak maka masuk ke taskQueue.
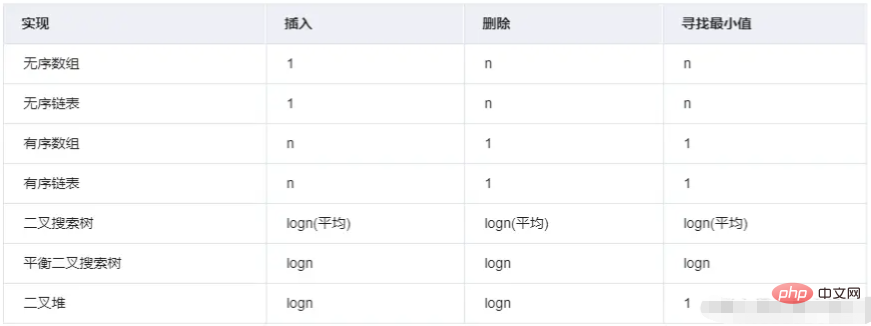
Bagaimana React menemukan tugas dengan prioritas tertinggi? Ambil taskQueue sebagai contoh. Ini adalah kumpulan tugas dinamis (antrian tugas), dan bentuk datanya adalah array. Tentu saja, Anda dapat mengurutkan berdasarkan prioritas, yaitu Array.sort. Ketika tugas baru ditambahkan ke antrian, tugas tersebut akan diurutkan terlebih dahulu, lalu tugas dengan prioritas tertinggi ditemukan dan dijalankan. Namun kompleksitas waktu rata-rata dari Array.sort adalah O(nlogn), yang bukan merupakan solusi terbaik.
SortIndex digunakan untuk mengurutkan di taskQueue newTask. Nilai ini diambil dari waktu kadaluwarsanya, artinya semakin tinggi prioritas tugas maka semakin banyak pula yang perlu dipahami dan dijalankan, sehingga waktu kadaluwarsanya akan semakin kecil semakin tinggi prioritasnya, semakin kecil waktunya, semakin kecil pula sortIndexnya. Faktanya, ini adalah antrian prioritas .
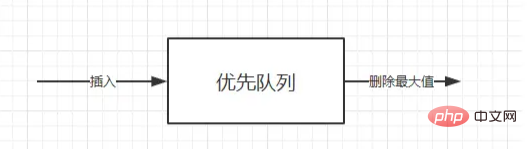
Antrian prioritas juga merupakan sejenis antrian ( pertama-tama, ini adalah antrian, dan kedua, tail in, first out ). Satu-satunya perbedaan adalah bahwa urutan dequeue dari antrian prioritas didasarkan pada prioritas; , Anda mungkin perlu mencari Elemen minimum atau maksimum dalam kumpulan elemen dapat dioperasikan dengan menggunakan ADT antrian prioritas. ADT antrian prioritas adalah struktur data yang mendukung operasi penyisipan dan penghapusan nilai minimum (mengembalikan dan menghapus elemen minimum) atau menghapus operasi nilai maksimum (mengembalikan dan menghapus elemen minimum).
Jika elemen dengan nilai kunci terkecil memiliki prioritas tertinggi, maka antrian prioritas ini disebut antrian prioritas menaik (yaitu, elemen terkecil selalu dihapus terlebih dahulu). Demikian pula, jika elemen dengan nilai kunci terbesar memiliki prioritas tertinggi, maka jenis antrian prioritas ini disebut antrian prioritas menurun (yaitu, elemen terbesar selalu dihapus terlebih dahulu karena kedua jenis ini simetris, Anda hanya perlu menghapusnya terlebih dahulu). untuk fokus pada salah satunya, seperti antrian prioritas menaik.
Misal : ketika kita sedang membeli tiket, kita semua sedang mengantri dan mempunyai prioritas yang sama. Siapapun yang berada di depan antrian akan membeli tiket terlebih dahulu. Namun kemudian ada tentara yang datang dan dia memiliki prioritas yang lebih tinggi dan langsung masuk dalam antrian . Bagian depan.
Tumpukan minimum (tumpukan akar kecil, tumpukan atas kecil...) digunakan di React untuk mencapai fungsi ini. Yaitu mengubah taskQueue menjadi heap minimum, kemudian mengambil tugas teratas untuk dieksekusi, menumpuk taskQueue, dan mempertahankannya sebagai struktur data heap minimum. Saat memasukkan tugas baru ke dalam taskQueue, tugas tersebut juga harus di-heap dan selalu disimpan sebagai heap minimum.
: Di beberapa tempat, heap disebut antrian prioritas (tidak akurat). Pertama-tama, itu adalah antrian dan memiliki ciri-ciri antrian, yaitu " masuk pertama, keluar pertama ". . Kedua, elemen dalam antrian ini memiliki prioritas, dan elemen dengan prioritas lebih tinggi akan menempati peringkat pertama.
Tepatnya, heap adalah cara untuk mengimplementasikan antrian prioritas. Tentu saja antrian prioritas juga dapat diterapkan dengan cara lain.
Kami telah mengatakan sebelumnya bahwa penyortiran heap adalah penyortiran yang tidak stabil, tetapi taskQueue berharap proses ini stabil. Artinya, jika mungkin waktu kedaluwarsa kedua tugas sama, maka itu tergantung siapa yang masuk pertama. Kumpulan tugas adalah nilai id dari tugas baru. Setiap kali ada tugas baru, id akan bertambah 1.
fungsi bandingkan(a, b) {
// Bandingkan indeks pengurutan terlebih dahulu, lalu id tugas.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ?diff : a.id - b.id;
} Sebelum memahami minimum heap, mari kita ulas pengetahuan dasarnya.
mengacu pada pohon terurut yang derajat simpulnya tidak lebih dari 2. Ini adalah pohon paling sederhana dan terpenting.
adalah pohon biner yang semua node pada setiap level mempunyai dua node anak, kecuali level terakhir yang tidak memiliki node anak.
Dari perspektif grafis, pohon biner penuh tampak seperti segitiga.
Jika jumlah level pohon biner adalah K dan jumlah node adalah (2^k) -1, maka pohon tersebut merupakan pohon biner penuh.
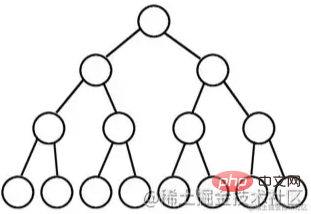
Pohon biner penuh berarti "anak perempuan memiliki kedua sisi" dan sangat sempurna, sehingga disebut pohon biner penuh.
tidak termasuk simpul daun, derajat semua simpul adalah 2. Dengan kata lain, derajat semua node hanya boleh 0 atau 2.
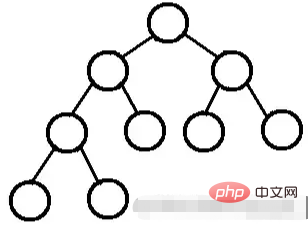
Pohon biner sempurna tidak mempunyai anak atau kedua anak.
Teks asli bahasa Inggris dari Pohon Biner Penuh:
Pohon Biner Penuh (FBT) adalah pohon yang setiap simpul selain daunnya mempunyai dua anak.
Teks asli bahasa Inggris dari pohon biner sempurna:
Pohon Biner Sempurna (PBT) adalah pohon dengan semua simpul daun pada kedalaman yang sama. Semua simpul internal memiliki derajat 2.
Semua buku asing mengacu pada buku teks terjemahan paling awal tentang pohon biner penuh dan pohon biner sempurna, tetapi artikel yang diterjemahkan paling awal diterjemahkan secara salah. Sekarang di China, kita hanya bisa melakukan kesalahan jika mereka salah (semua orang salah, maka yang salah juga benar. Misalnya pelobi...). Jika Anda ingin mendiskusikan kedua konsep ini dengan teman asing, sebaiknya perhatikan.
Pohon Biner(CBT) adalah pohon biner yang setiap levelnya, kecuali mungkin yang terakhir, terisi penuh, dan semua node berada sejauh mungkin di kiri.
Sebuah pohon biner dengan kedalaman n node k, beri nomor pada node-node tersebut pohon dari atas ke bawah dan dari kiri ke kanan. Jika simpul bernomor i (1≤i≤n) berada pada pohon biner dengan simpul bernomor i pada pohon biner lengkap, Jika posisinya sama maka pohon binernya adalah disebut pohon biner lengkap.
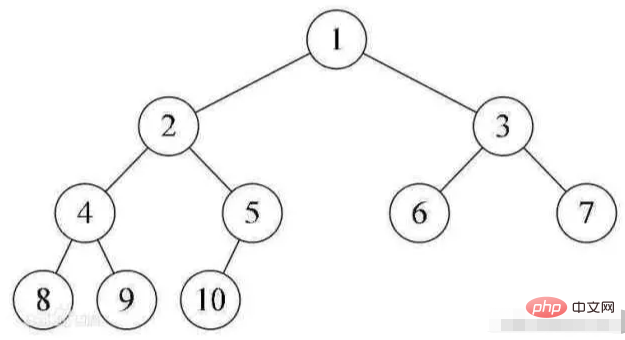
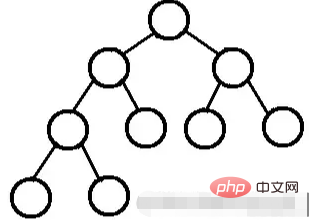
Heap selalu memenuhi sifat-sifat berikut:
pertama-tama kita harus memahami tumpukan akar besar dan tumpukan akar kecil. Dalam pohon biner lengkap Semua node lebih besar (atau lebih kecil) dari node turunannya, jadi ada dua situasi di sini, tumpukan maksimum dan tumpukan minimum.
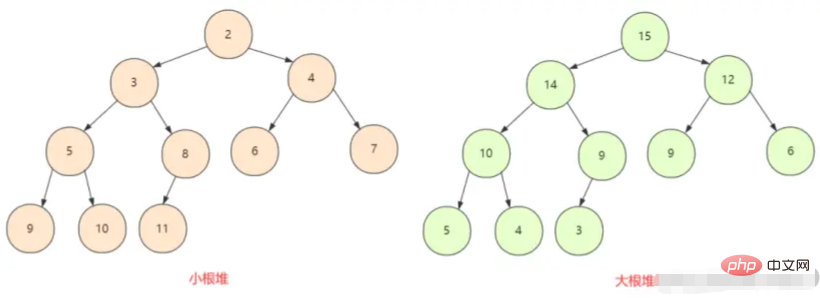
Heap biasanya berupa array objek yang dapat dilihat sebagai pohon biner lengkap . Tentu saja, pohon biner juga dapat direpresentasikan dengan array.
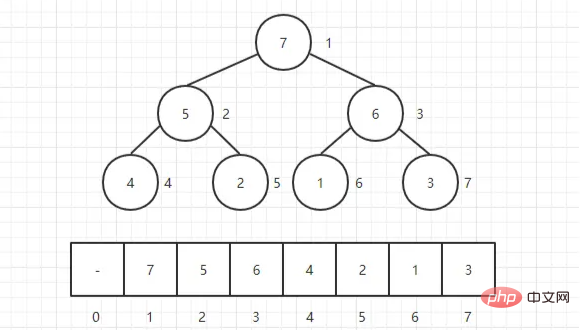
adalah membangun heap terlebih dahulu dan kemudian menyesuaikannya.
, untuk pohon biner (representasi array), kita menyesuaikan dari bawah ke atas, dimulai dari "node non-daun pertama" dan menyesuaikan ke depan. Aturan penyesuaiannya adalah sebagai berikut:
Membangun heap adalah O(n ) proses kompleksitas waktu.
① Mulailah dari node non-leaf pertama untuk menilai swap ke bawah (shiftDown), sehingga node dan anak saat ini dapat mempertahankan properti heap
② Namun, penggantian node biasa mungkin tidak menjadi masalah. Jika pertukaran merusak properti struktur heap dari anak tersebut, maka harus dilakukan ShiftDown ulang pada node yang ditukar sampai berhenti.
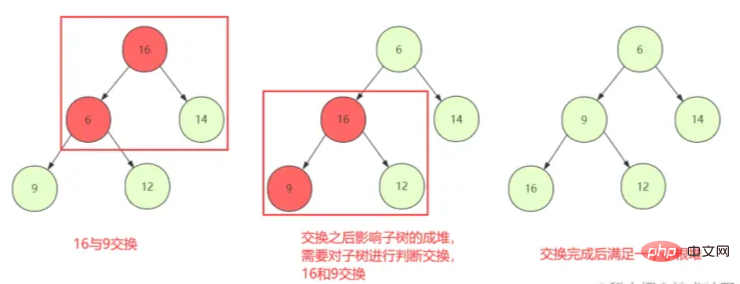
heap
disesuaikanMenghancurkan struktur tumpukan.
① Jadi cukup letakkan elemen terakhir terlebih dahulu. Dengan cara ini, Anda hanya perlu menilai pergeseran swap (shiftDown), namun perlu diperhatikan bahwa ukuran seluruh heap telah berubah saat ini Secara logis kami tidak akan menggunakan posisi yang dibuang, jadi kami perlu menyertakan heap parameter ukuran saat mendesain fungsi.
② Ulangi operasi di atas hingga semua elemen di heap diperoleh.
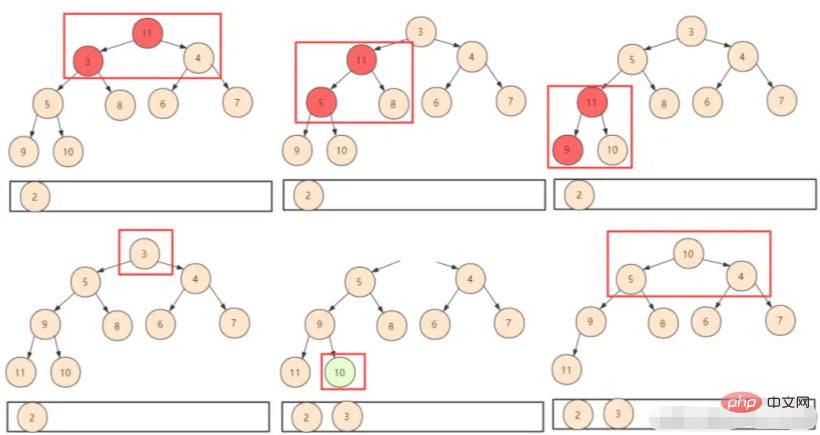
Dalam hal analisis kompleksitas algoritma heap, kompleksitas waktu pembangunan heap sebelumnya adalah O(n). Setiap kali bagian atas heap dihapus dan kemudian ditukar ke bawah, nomor masing-masing heap akan dicatat. Dengan cara ini, kompleksitasnya adalah O(nlogn), dan total kompleksitas waktu adalah O(n)+O(nlogn)=O(nlogn).
Heap cocok untuk menjaga nilai maksimal dari koleksi.
Setelah sebuah elemen dikeluarkan dari heap, biaya penyesuaian ulang untuk mendapatkan elemen teratas dari heap (yaitu, nilai tertinggi kedua) relatif rendah, karena setelah elemen tersebut dikeluarkan, heap menjadi semi -produk jadi, dan nilai tertinggi kedua diperoleh dari produk setengah jadi. Tentu saja biayanya relatif rendah, dan kompleksitas waktunya adalah O(logn), namun jika dilalui satu kali untuk mencari nilai tertinggi kedua, kompleksitas waktu adalah O(n).
Kodeditulis dalam Javascript ES6.
kelasTumpukan {
konstruktor(data, kompilasi) {
ini.data = data ?data : [];
// Aturan perbandingan: lebih fleksibel, Anda dapat membandingkan nilai atau objek this.compartor = comp ? comp : (ab) => ab;
// Sesuaikan dengan heap (antrian prioritas)
ini.heapify();
}
menumpuk() {
if(ini.ukuran() <= 1) kembali;
// Mulai penyesuaian dari node non-daun pertama, atau Anda dapat menyesuaikan dari elemen terakhir for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Sesuaikan heap. Penyesuaian ke bawah juga dapat diimplementasikan menggunakan rekursi. Di sini, iterasi digunakan untuk mengimplementasikan this.shiftDown(i);
}
}
// Sesuaikan shift ke bawah(i) {
misalkan kiri = 2*i +1;
biarkan kanan = 2*i +2;
biarkan len = ini.ukuran();
sementara(saya < len) {
biarkan findIndex = i;
//Anak kiri "lebih besar"
if(kiri < len && this.compartor(ini.data[kiri], ini.data[findIndex]) < 0) {
findIndex = kiri;
}
// Anak yang tepat adalah "lebih besar"
if(kanan < len && this.compartor(ini.data[kanan], ini.data[findIndex]) < 0) {
findIndex = kanan;
}
jika(saya !== temukanIndeks) {
//Tukarkan node saat ini dengan nilai yang lebih besar [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// Setelah menyesuaikan lapisan ini, mungkin mempengaruhi karakteristik heap lapisan bawah, jadi terus sesuaikan lapisan bawah (implementasi berulang, atau rekursif)
i = temukanIndeks;
kiri = 2*i +1;
kanan = 2*i +2;
}
kalau tidak {
// Jika tidak diperlukan penyesuaian, lompat keluar (harus melompat keluar, jika tidak, loop tidak dapat diakhiri)
merusak;
}
}
}
// Sesuaikan shiftUp(i){
// Temukan subskrip dari induk let parentIndex = Math.floor((i-1)/2);
// Sesuaikan maksimum ke 0
while(indeks induk >=0 ) {
biarkan findIndex = i;
if(ini.compartor(ini.data[parentIndex], ini.data[findIndex]) > 0) {
findIndex = indeks induk;
}
jika(findIndex !== i) {
[ini.data[i], ini.data[findIndex]] = [ini.data[findIndex], ini.data[i]];
i = temukanIndeks;
parentIndex = Matematika.lantai((i-1)/2);
}
kalau tidak {
merusak;
}
}
}
// Dapatkan jumlah semua elemen dalam ukuran heap(){
kembalikan ini.data.panjang;
}
// Dapatkan elemen pertama dari heap peek(){
if(!this.size()) mengembalikan nol;
kembalikan ini.data[0];
}
//Tambahkan elemen ke heap push(x){
ini.data.push(x);
this.shiftUp(ini.data.panjang-1);
}
// Memunculkan elemen pertama dari heap pop(){
if(!this.size()) mengembalikan nol;
biarkan res = ini.data[0];
if(ini.ukuran() == 1) {
ini.data.pop();
}
kalau tidak {
ini.data[0] = ini.data[ini.data.panjang-1];
ini.data.panjang = ini.data.panjang-1;
ini.shiftDown(0);
}
kembalikan res;
}
} misalkan arr = [2,9,8,6,3,10,5,7,4,1];
misalkan comp = (a, b) => ab;
biarkan heap = new Heap(arr, comp);
misalkan res = [];
while(tumpukan.ukuran()) {
res.push(heap.pop());
}
console.log(res); Elemen dalam arr juga bisa berupa objek.
Direktori paket/penjadwal dalam kode sumber React adalah kode yang terkait dengan modul penjadwalan tugas React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Hak Cipta (c) Facebook, Inc. dan afiliasinya.
*
* Kode sumber ini dilisensikan di bawah lisensi MIT yang terdapat di
* File LISENSI di direktori root pohon sumber ini.
*
* @aliran ketat
*/
ketik Tumpukan = Array<Node>;
ketik Node = {|
ID: nomor,
sortIndex: nomor,
|};
fungsi ekspor push(heap: Heap, node: Node): void {
indeks const = tumpukan.panjang;
heap.push(simpul);
siftUp(tumpukan, simpul, indeks);
}
fungsi ekspor mengintip (heap: Heap): Node |.
const pertama = tumpukan[0];
kembali dulu === tidak terdefinisi null : pertama;
}
fungsi ekspor pop(heap: Heap): Node |.null {
const pertama = tumpukan[0];
if (pertama !== tidak terdefinisi) {
const terakhir = heap.pop();
if (terakhir !== pertama) {
tumpukan[0] = terakhir;
siftDown(tumpukan, terakhir, 0);
}
kembali dulu;
} kalau tidak {
kembalikan nol;
}
}
fungsi siftUp(tumpukan, simpul, i) {
biarkan indeks = i;
sementara (benar) {
const parentIndex = (indeks - 1) >>> 1;
const induk = tumpukan[indeks induk];
if (induk !== tidak terdefinisi && bandingkan(induk, simpul) > 0) {
// Induknya lebih besar. Tukar posisi.
heap[parentIndex] = simpul;
heap[index] = induk;
indeks = indeks induk;
} kalau tidak {
// Induknya lebih kecil.
kembali;
}
}
}
fungsi siftDown(tumpukan, simpul, i) {
biarkan indeks = i;
const panjang = tumpukan.panjang;
while (indeks < panjang) {
const leftIndex = (indeks + 1) * 2 - 1;
const kiri = tumpukan[indeks kiri];
const indeks kanan = indeks kiri + 1;
const kanan = tumpukan[indeks kanan];
// Jika node kiri atau kanan lebih kecil, tukar dengan node yang lebih kecil.
if (kiri !== tidak terdefinisi && bandingkan(kiri, simpul) < 0) {
if (kanan !== tidak terdefinisi && bandingkan(kanan, kiri) < 0) {
tumpukan[indeks] = kanan;
tumpukan[indeks kanan] = simpul;
indeks = kananIndeks;
} kalau tidak {
tumpukan[indeks] = kiri;
tumpukan[indeks kiri] = simpul;
indeks = indeks kiri;
}
} else if (kanan !== tidak terdefinisi && bandingkan(kanan, simpul) < 0) {
tumpukan[indeks] = kanan;
tumpukan[indeks kanan] = simpul;
indeks = kananIndeks;
} kalau tidak {
// Tidak ada anak yang lebih kecil.
kembali;
}
}
}
fungsi bandingkan(a, b) {
// Bandingkan indeks pengurutan terlebih dahulu, lalu id tugas.
const diff = a.sortIndex - b.sortIndex;
return diff !== 0 ?diff : a.id - b.id;
} Minimum heap yang kita implementasikan sedikit berbeda dengan implementasi di React, namun idenya sama, hanya kode penulisannya saja yang berbeda.
penjadwalan tugas di React diimplementasikan menggunakan heap minimum. Jika kita memiliki pemahaman tertentu tentang heap minimum sebelumnya, kita akan mempelajari konten ini lebih cepat. Secara pribadi, menurut saya betapa pentingnya mengumpulkan pengetahuan pada tahap awal, tetapi proses ini mungkin membosankan. Saat ini, apakah Anda pikir Anda mengetahui beberapa algoritme? Sebenarnya, algoritme ini adalah level awal, dan Anda bahkan belum memulainya. Karena dalam skenario penjadwalan tugas React, persyaratan yang akan diterapkan sangat jelas, dan struktur data serta algoritma yang akan digunakan juga jelas. Dalam beberapa skenario aktual, kita mengetahui persyaratan spesifiknya, tetapi kita tidak tahu hasil data dan algoritme apa yang akan digunakan. Kita perlu mengabstraksi persyaratan dan merancang struktur data dan algoritme tertentu berdasarkan model data abstrak .