強化学習によってハノイの塔のパズルを解きます。
Numpy と Pandas がインストールされている Python 環境で、スクリプトhanoi.pyを実行して、「結果」セクションに示されている 3 つのプロットを生成します。たとえば、異なる数のディスクNでゲームをプレイするようにスクリプトを簡単に適合させることができます。
最近、Google Deepmind の AlphaGo が人間のプロ棋士を破ったことで、強化学習に新たな関心が集まっています。ここでは、より単純なパズル、ハノイの塔ゲームが解決されます。この実装は、Watkins & Dayan [1] によって最初に提案された Q 学習アルゴリズムに従います。
ハノイの塔ゲームは、3 本のペグと、ペグ上でスライドできるさまざまなサイズの多数のディスクで構成されています。パズルは、すべてのディスクが最初のペグに昇順で積み重ねられることから始まります。最大のディスクが下に、最小のディスクが上にあります。ゲームの目的は、すべてのディスクを 3 番目のペグに移動することです。唯一の正当な移動は、最上位のディスクを 1 つのペグから別のペグに移動する移動です。ただし、ディスクをより小さいディスクの上に置くことはできません。図 1 は、4 つのディスクの最適なソリューションを示しています。

図 1. 4 枚のディスクのハノイの塔パズルのアニメーションによる解決策。 (出典: ウィキペディア)。
Anderson [2] に従って、ゲームの状態をタプルで表します。ここで、 i番目の要素は、 i番目のディスクがどのペグにあるかを示します。ディスクには、サイズの大きい順にラベルが付けられます。したがって、初期状態は (111) であり、望ましい最終状態は (333) です (図 2)。
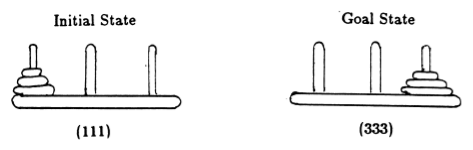
図 2. 3 つのディスクを使用したハノイの塔パズルの初期状態と目標状態。 ([2]より)。
パズルの状態と、合法的な動きに対応するそれらの間の遷移は、パズルの状態遷移グラフを形成します (図 3 を参照)。
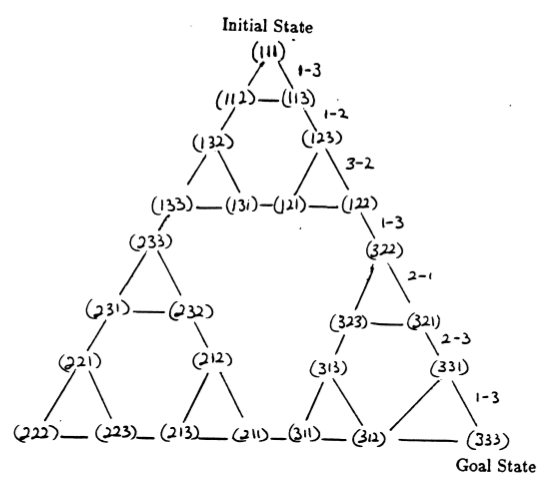
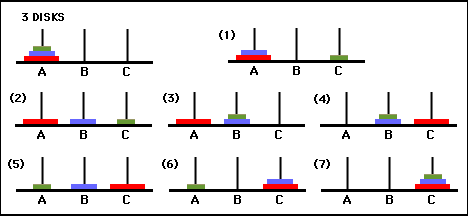
図 3. 3 つのディスクからなるハノイの塔パズルの状態遷移グラフ (上) と、グラフの右側のパスをたどる、対応する最適な 7 手の解決策 (下)。 ([2] および Mathforum.org より)。
ハノイの塔パズルを解くのに必要な最小手数は 2 N - 1 ( Nはディスクの数) です。したがって、 N = 3 の場合、図 3 に示すように、パズルは 7 手で解くことができます。次のセクションでは、これが Q 学習によってどのように達成されるかを概説します。
Rと「アクション値」行列Qプログラムの最初のステップは、ゲームのルールを捉え、ゲームに勝つと報酬を与える報酬行列Rを生成することです。わかりやすくするために、 N = 2ディスクの報酬行列を図 4 に示します。
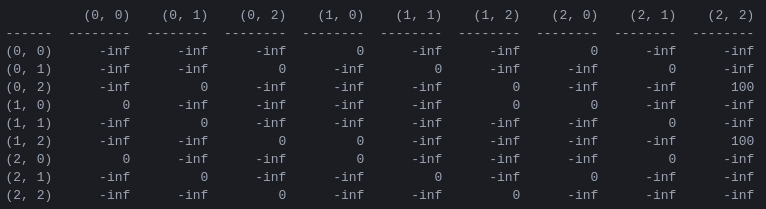
図 4. N = 2ディスクを使用したハノイの塔パズルの報酬行列R ( i , j ) 番目の要素は、状態iからjへの移動に対する報酬を表します。状態は、図 2 および 3 のようにタプルによってラベル付けされますが、ペグが 1 から 3 ではなく 0 から 2 に「Python 的に」インデックス付けされる点が異なります。目標状態 (2,2) につながる動きには報酬が割り当てられます。 100、不正な手は 、その他のすべての手は 0 です。
報酬行列R即時の報酬のみを記述します。100 の報酬は最後から 2 番目の状態 (0,2) と (1,2) からのみ達成できます。他の状態では、2 つまたは 3 つの可能な手はそれぞれ 0 の等しい報酬を持ち、一方を他方よりも選択する明白な理由はありません。
最終的に、私たちは各状態で考えられるそれぞれの動きに「値」を割り当て、これらの値を最大化することで最適な解決策につながるポリシーを定義できるように努めます。各状態の各アクションの「値」の行列はQと呼ばれ、Watkins & Dayan [1] によって説明されているように、確率論的な方法で再帰的に解決または「学習」できます。 2 つのディスクの結果を図 5 に示します。
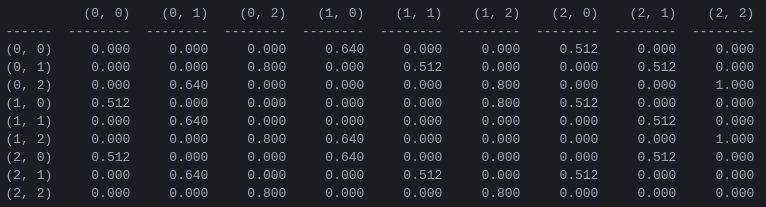
図 5. 2 つのディスクを使用したハノイの塔ゲームの「アクション値」行列Q割引係数 = 0.8、学習係数 = 1.0、トレーニング エピソード 1000 で学習されました。
行列Qの値は基本的に、図 3 の状態遷移グラフの頂点に割り当てることができる重みであり、エージェントを初期状態から目標状態まで可能な限り最短の方法で導きます。この例では、状態 (0,0) から開始し、 Qの最も高い値を持つ手を連続して選択することで、読者はQ行列が状態 (0,0) ~ (1) のシーケンスを通じてエージェントを導くことを確信できます。 ,0) - (1,2) - (2,2)。これは、2 ディスクのハノイの塔ゲームの 3 手の最適解に対応します (図 6)。
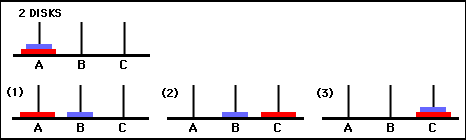
図 6. 2 枚のディスクを使用したハノイの塔ゲームのソリューション。連続する状態はそれぞれ (0,0)、(1,0)、(1,2)、(2,2) で表されます。 (出典: mathforum.org)。
この例では、行列Q最適値に収束しており、定常ポリシーが定義されています。各行には、一意の最大値を持つ 1 つのアクションが含まれています。ただし、学習プロセス中、さまざまなアクションが同じQ値を持つ可能性があります。 (特に、 Qがゼロの行列に初期化されるトレーニングの開始時にこれが当てはまります)。次のセクションで示すシミュレーションでは、そのような状況は次の確率論的ポリシーによって処理されます。最大 Q 値が複数のアクション間で共有される場合、これらのアクションの 1 つをランダムに選択します。
Q 学習アルゴリズムのパフォーマンスは、ハノイの塔パズルを解くのにかかる (平均) 手の数を数えることによって測定できます。この数はトレーニング エピソードの数とともに減少し、最終的に最適値 2 N - 1 に達します。ここで、 Nはディスクの数です (図 7 のN = 2、3、および 4 の場合)。
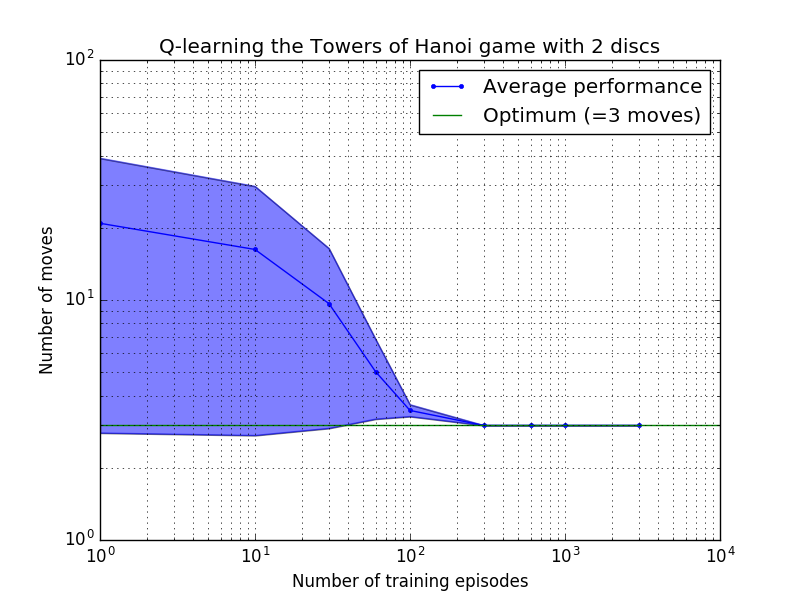
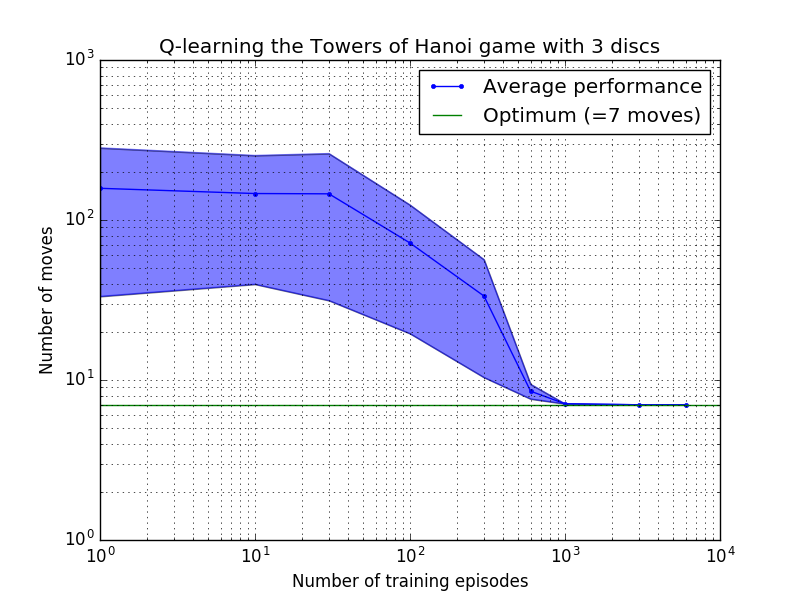
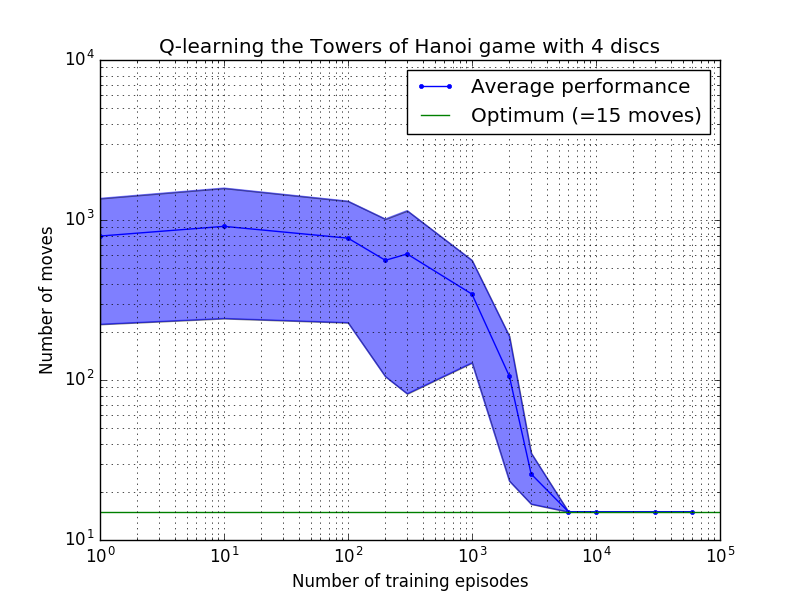
図 7.上から順に 2 枚、3 枚、4 枚のディスクを使用したハノイの塔ゲームの Q 学習アルゴリズムのパフォーマンス。すべてのケースで、学習は割引係数 = 0.8、学習係数 = 1.0 で実行されました。青い実線の曲線は、結果として得られる各確率論的ポリシーについて、トレーニングとゲームの 100 回プレイの 100 エポックにわたる平均パフォーマンスを表しています。青色の影付き領域の上限と下限は、推定標準偏差によって平均からオフセットされます。 ( N = 3 とN = 4 の場合、計算上の制約により、トレーニング エピソードの数と再生時間はそれぞれ 10 と 10 に減りました)。
図 7 の学習特性の興味深い特徴は、どのケースでも最初は学習が遅く、エージェントはランダムに動きを選択する「ゼロ トレーニング」ポリシーよりも優れたパフォーマンスを発揮することがほとんどないことです。ある時点で学習は「変曲点」に達し、その後加速したペースで最適な手数に収束します (ただし、これは対数スケールにより多少誇張されています)。
Python スクリプトは、Q 学習により、任意の数のディスクに対してハノイの塔のパズルを最適に解くことに成功しました。このスクリプトは、異なる報酬行列Rを使用する他の問題にも簡単に適応できます。
最適な解に収束するために必要なトレーニング エピソードの数は、ディスクNの数に応じて大幅に増加します。N N=2ディスクの場合は約 300 エピソードかかりますが、 N=4の場合は約 6,000 エピソードかかります。学習アルゴリズムの可能な改善は、Hengst [3] によって行われたように、再帰的解を自動的に検索できるようにすることです。
[1] Watkins & Dayan、 Q ラーニング、機械学習、8、279-292 (1992)。 (PDF)。
[ 2 ] Anderson、多層コネクショニスト システムによる学習と問題解決、博士号論文(1986)。 (PDF)。
[3] Hengst、 Discovering Hierarchy in Reinforcement Learning with HEXQ 、第 19 回機械学習国際会議議事録 (2002)。 (PDF)。