@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Neurodiffeq はソリューション バンドルをサポートしており、逆問題の解決に使用できることをご存知ですか?ここを見てください!
?ニューロディフェクについてはもうご存知ですか? ?よくある質問にジャンプします。
neurodiffeq 、ニューラル ネットワークを使用して微分方程式を解くためのパッケージです。微分方程式は、ある関数とその導関数を関連付ける方程式です。それらはさまざまな科学および工学分野で出現します。従来、これらの問題は数値的手法 (有限差分、有限要素など) によって解決できました。これらの方法は効果的かつ適切ですが、その表現可能性は関数表現によって制限されます。連続で微分可能な微分方程式の解を計算できれば興味深いでしょう。
汎用関数近似器として、人工ニューラル ネットワークは、特定の初期/境界条件で常微分方程式 (ODE) および偏微分方程式 (PDE) を解く可能性があることが示されています。 neurodiffeqの目的は、ANN を使用して微分方程式を解く既存の手法を実装し、ソフトウェアが広範なユーザー定義の問題に十分に対処できる柔軟性を実現できるようにすることです。
ほとんどの標準ライブラリと同様に、 neurodiffeqは PyPI でホストされています。最新の安定版リリースをインストールするには、
pip install -U Neurodiffq # '-U' は最新バージョンへのアップデートを意味します
あるいは、ライブラリを手動でインストールして、新機能に早期にアクセスすることもできます。これは、ライブラリに貢献したい開発者に推奨される方法です。
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd Neurodiffeq && pip install -r 要件 pip インストール 。 # ライブラリに変更を加えるには、`pip install -e .`pytest testing/ を使用します。 # テストを実行します。オプション。
ご質問がございましたら、喜んでお手伝いさせていただきます。それまでの間、よくある質問をご覧ください。
neurodiffeqの完全なチュートリアルとドキュメントを表示するには、公式ドキュメントを確認してください。
ドキュメントに加えて、最近、スライドを含む簡単なウォークスルー デモ ビデオを作成しました。
neurodiffeq からインポート difffrom Neurodiffeq.solvers import Solver1D、Solver2Dneurodiffeq.condition からインポート IVP、DirichletBVP2Dneurodiffeq.networks からインポート FCNN、SinActv
ここでは、ロトカ-ヴォルテラ方程式として知られる 2 つの ODE の非線形システムを解きます。 2 つの未知関数 ( uおよびv ) と 1 つの独立変数 ( t ) があります。
def ode_system(u, v, t): 戻り値 [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]条件 = [IVP(t_0=0.0, u_0=1.5 )、IVP(t_0=0.0、u_0=1.0)]nets = [FCNN(actv=SinActv)、 FCNN(actv=SinActv)]solver = Solver1D(ode_system, 条件, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution =solver.get_solution()
solution呼び出し可能なオブジェクトであり、次のように numpy 配列または torch tensor を渡すことができます。
u, v = solution(t, to_numpy=True) # t は np.ndarray または torch.Tensor にすることができます
uとv解析解に対してプロットすると、次のような結果が得られます。
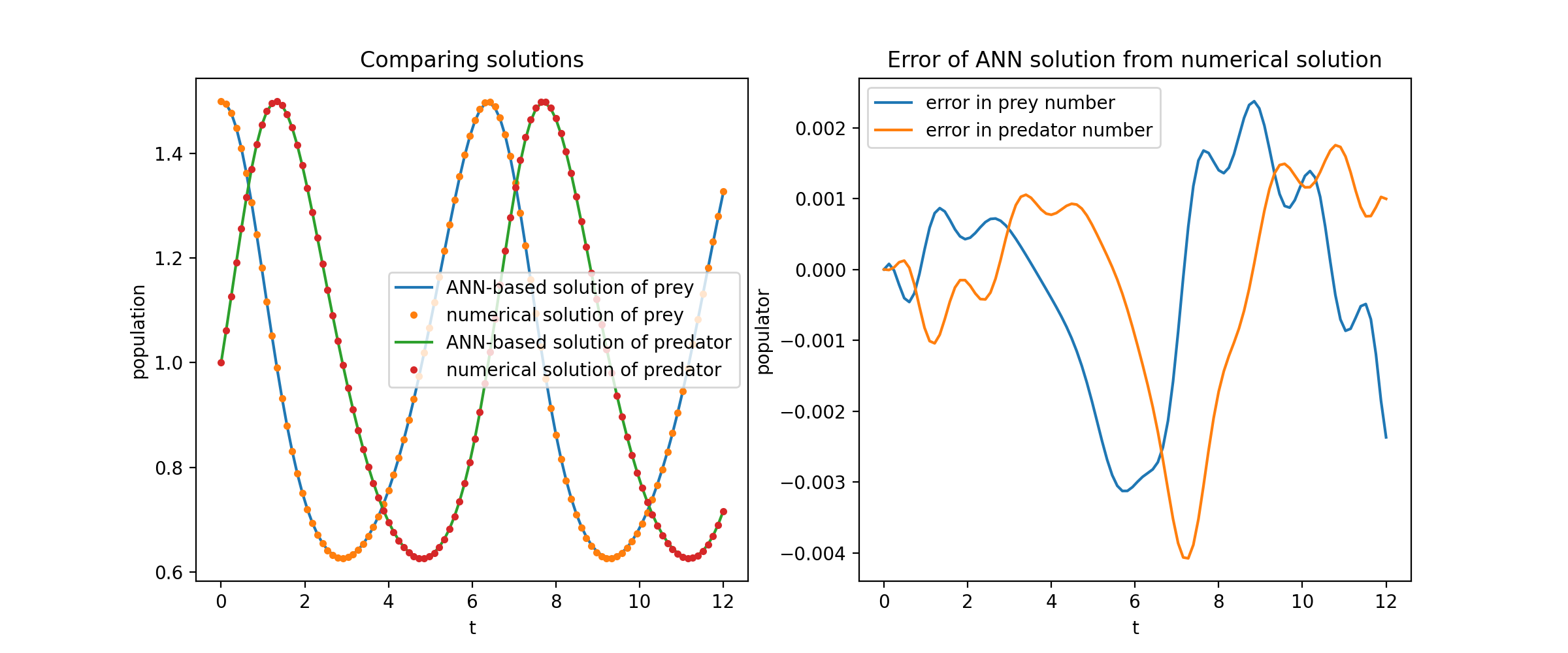
ここでは、長方形上でディリクレ境界条件を使用してラプラス方程式を解きます。解析解の計算を簡単にするためにラプラス方程式を選択することに注意してください。実際には、ソルバーを十分に調整すれば、任意の非線形カオス偏微分方程式を試すことができます。
2 次元 PDE 系の解法は ODE の解法と非常に似ていますが、境界値問題には2 つの変数xとy 、初期境界値問題にはxとtがあり、どちらもサポートされている点が異なります。
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: トーチ。 sin(np.pi*y)、x_max=1、x_max_val=ラムダ y: 0、y_min=0、 y_min_val=ラムダ x: 0、y_max=1、y_max_val=ラムダ x: 0、
)
]nets = [FCNN(n_input_units=2, n_output_units=1, hidden_units=(512,))]solver = Solver2D(pde_system, 条件, xy_min=(0, 0), xy_max=(1, 1), nets=nets) solver.fit(max_epochs=2000)solution =solver.get_solution() 2D PDE のsolutionの特徴は ODE のそれとは若干異なります。繰り返しますが、numpy 配列または torch テンソルのいずれかを受け取ります。
u = ソリューション(x, y, to_numpy=True)
[0,1] × [0,1]で u を評価すると、次のプロットが得られます。
| ANNベースのソリューション | 偏微分方程式の残差 |
|---|---|
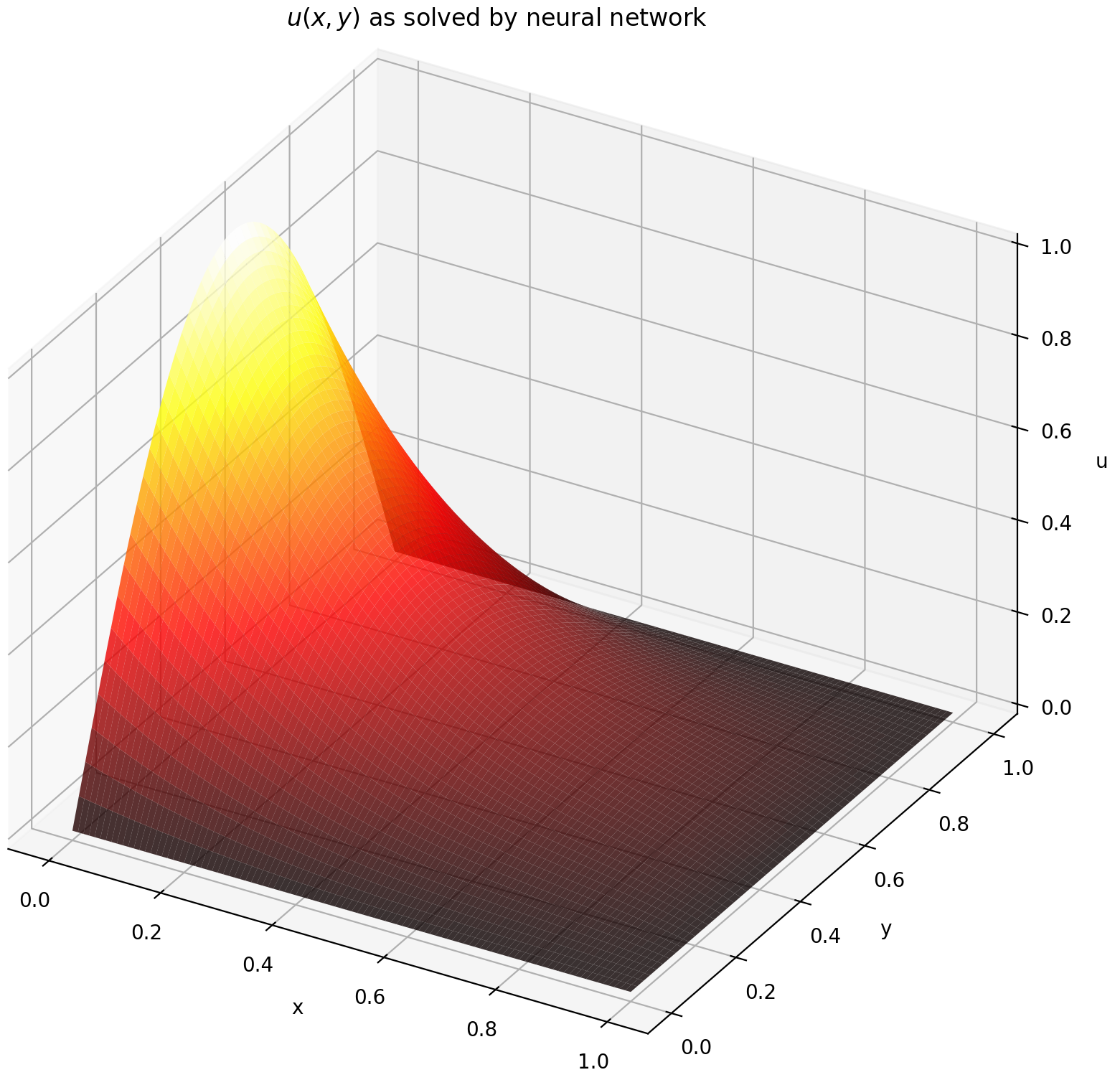 | 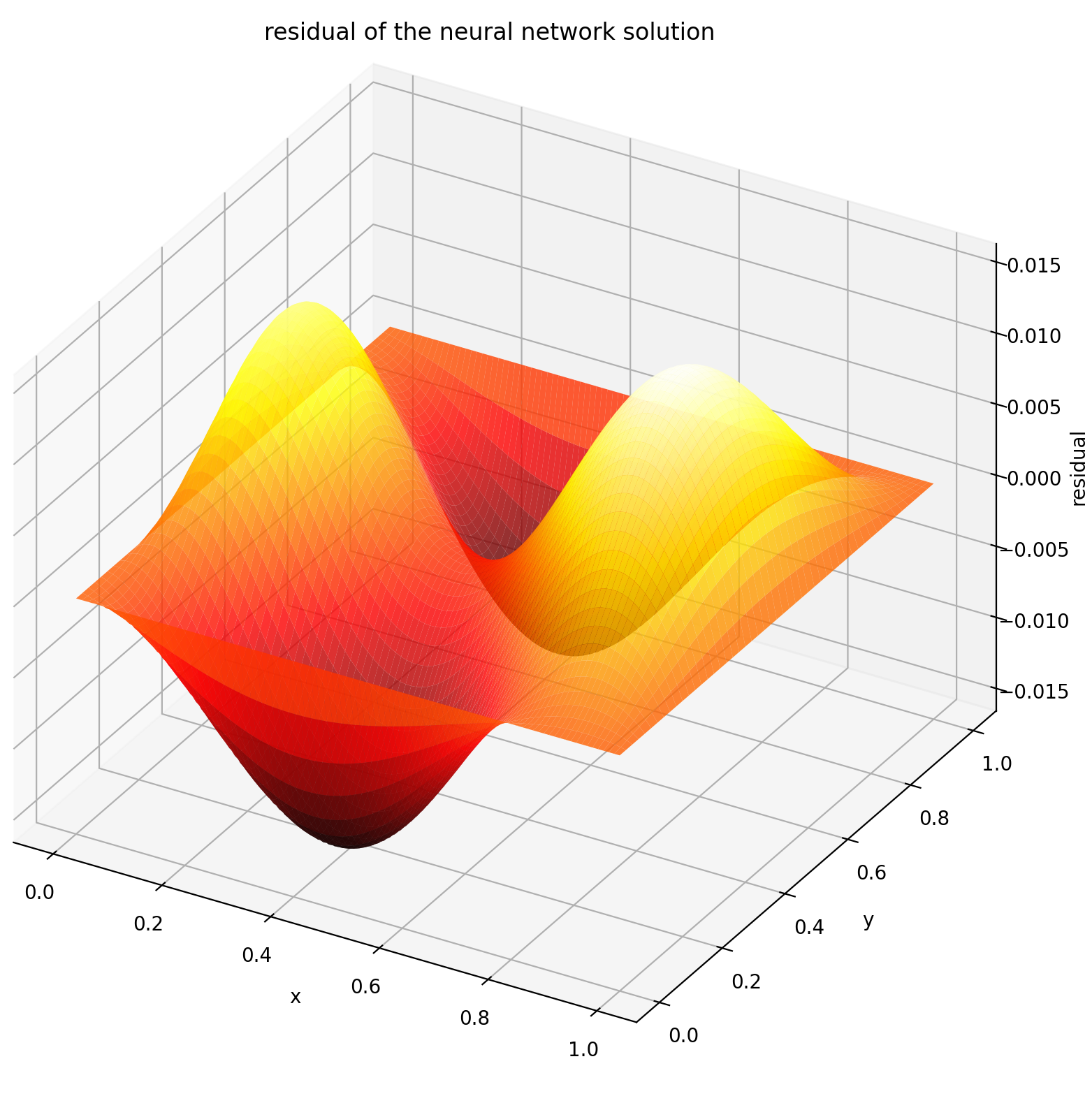 |
モニターは、PDE/ODE ソリューション、損失の履歴、トレーニング中のカスタム メトリックを視覚化するためのツールです。 Jupyter Notebook ユーザーは、 %matplotlib notebookマジックを実行する必要があります。 Jupyter Lab ユーザーの場合は、 %matplotlib widgetを試してください。
neurodiffeq.monitors から import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
プロットが100 エポックごとおよび最後のエポックごとに更新され、2 つのプロットが表示されます。1 つは区間[0,12]での解の視覚化であり、もう 1 つは損失履歴 (トレーニングと検証) です。
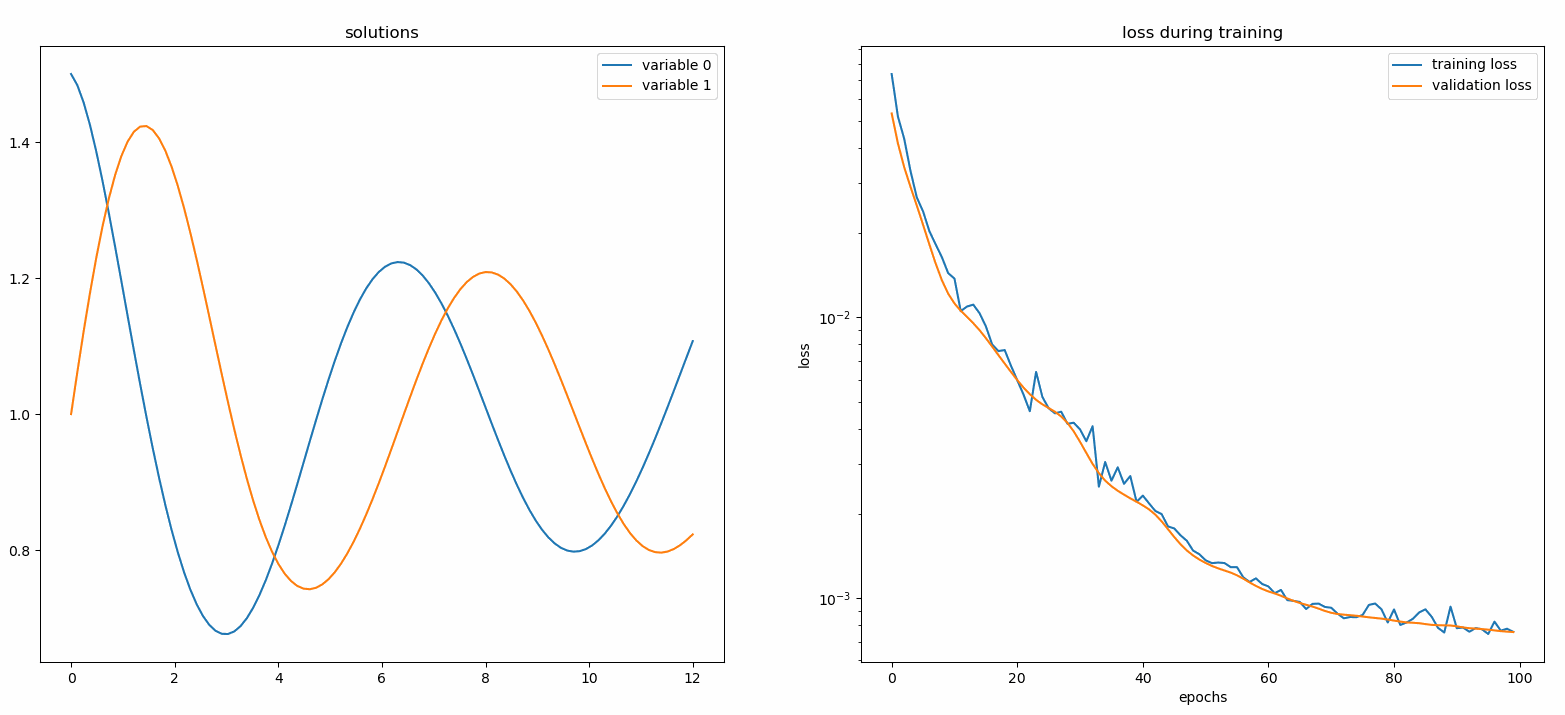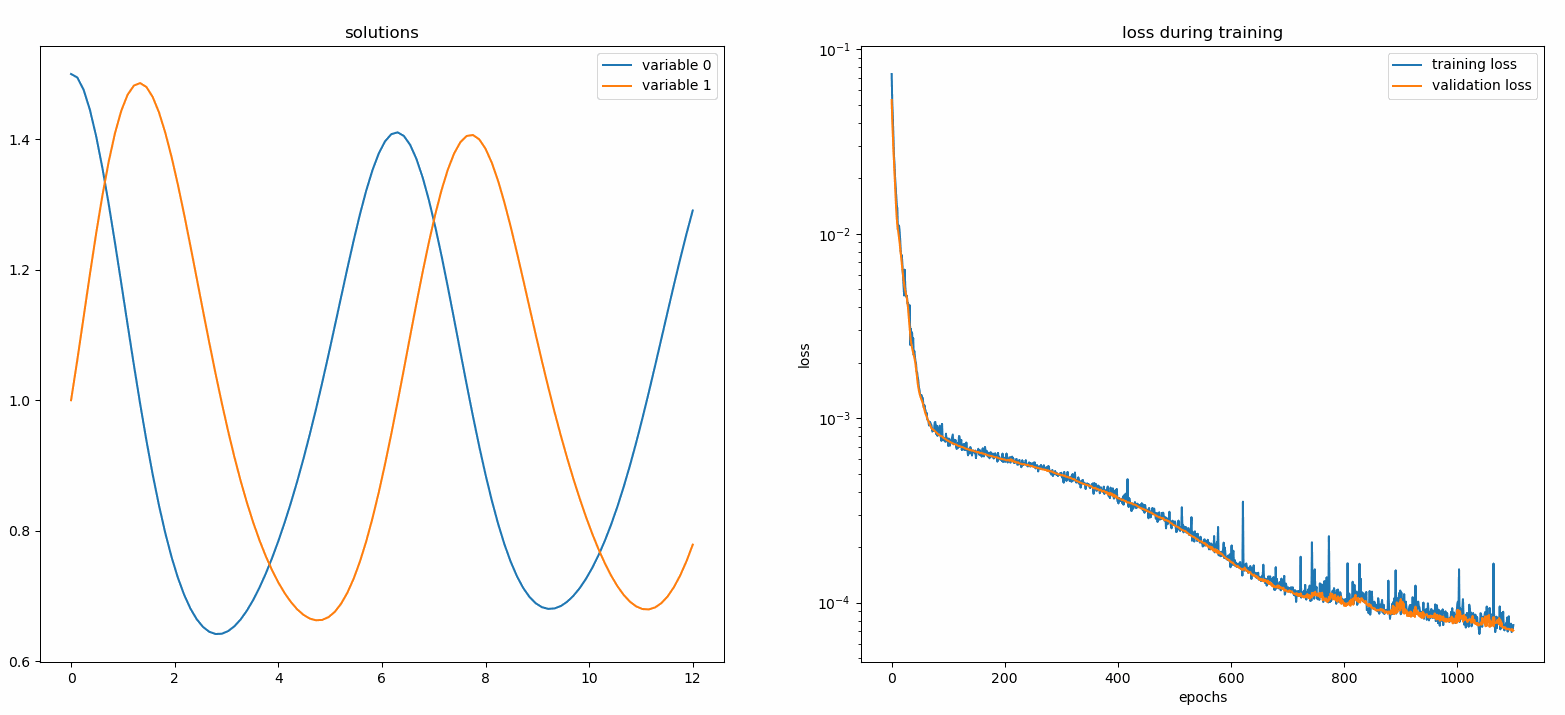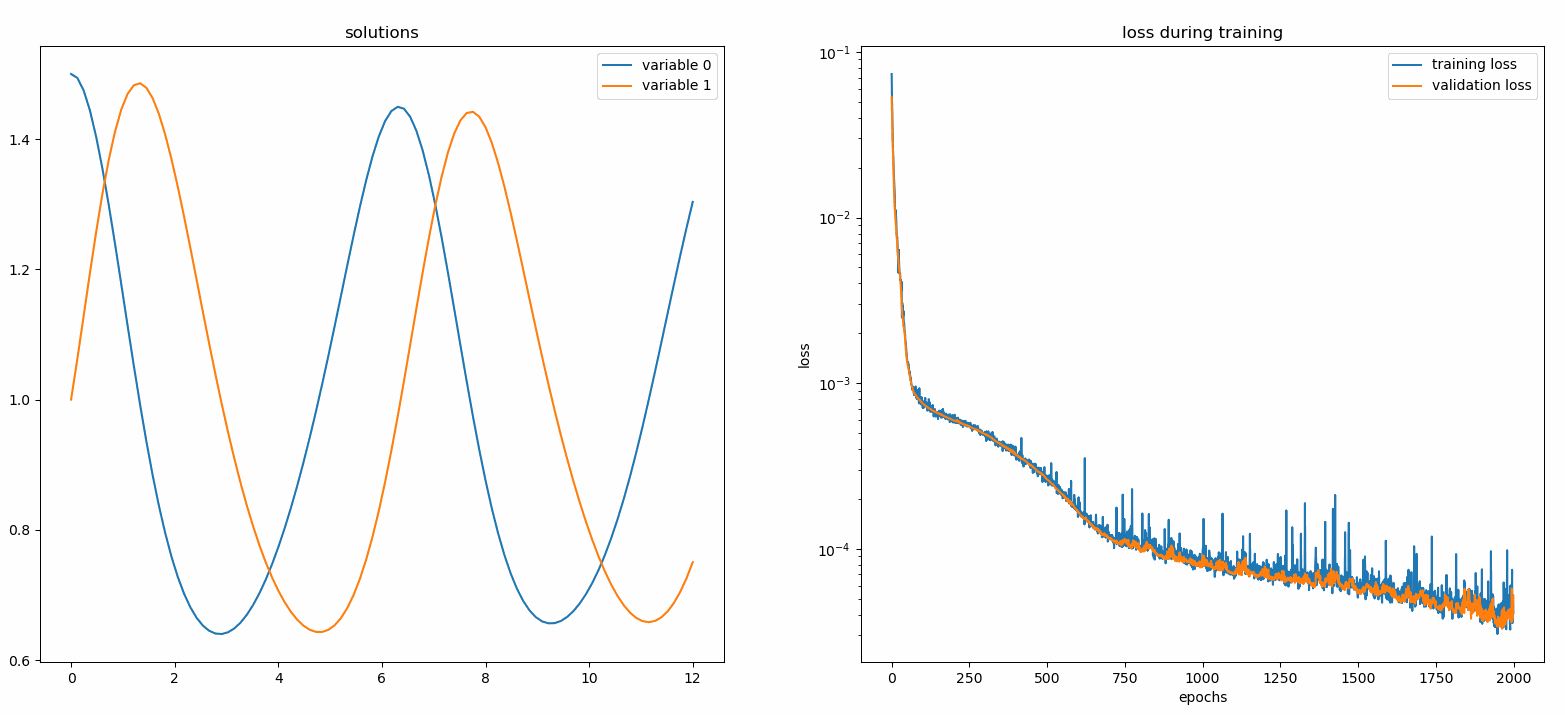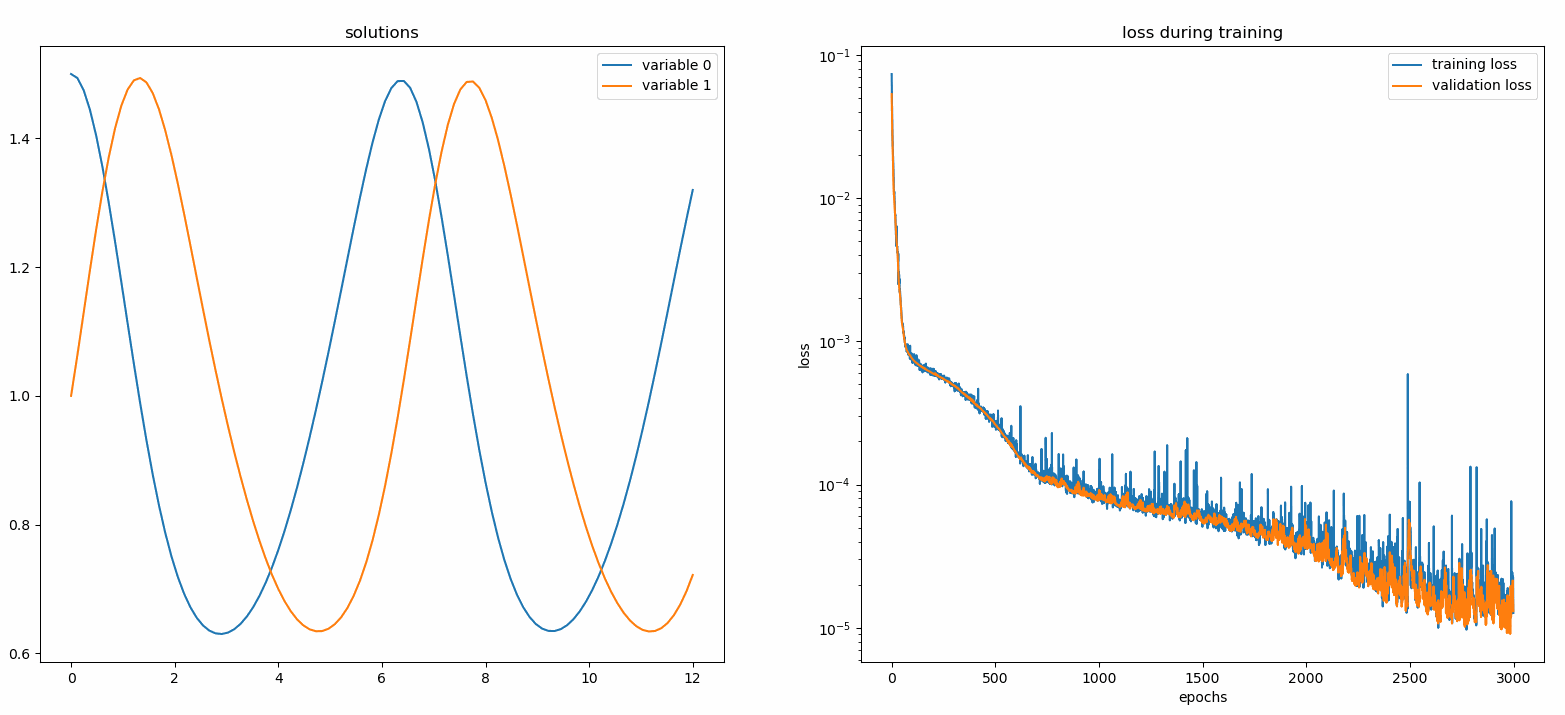
便宜上、 FCNN (隠れユニットと活性化関数をカスタマイズできる完全接続ニューラル ネットワーク) を実装しました。
neurodiffeq.networks からインポート FCNN# デフォルト: n_input_units=1、n_output_units=1、hidden_units=[32, 32]、activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., hidden_units=[ ..., ..., ...]、アクティベーション=...) ...ネット = [ネット1、ネット2、...]
通常、 FCNN出発点として適しています。上級ユーザーの場合、ソルバーはカスタムtorch.nn.Moduleと互換性があります。唯一の制約は次のとおりです。
モジュールは形状(None, n_coords)のテンソルを受け取り、形状(None, 1)のテンソルを出力します。
solver = Solver(..., nets=nets)に渡すnetsには、合計n_funcsモジュールが必要です。
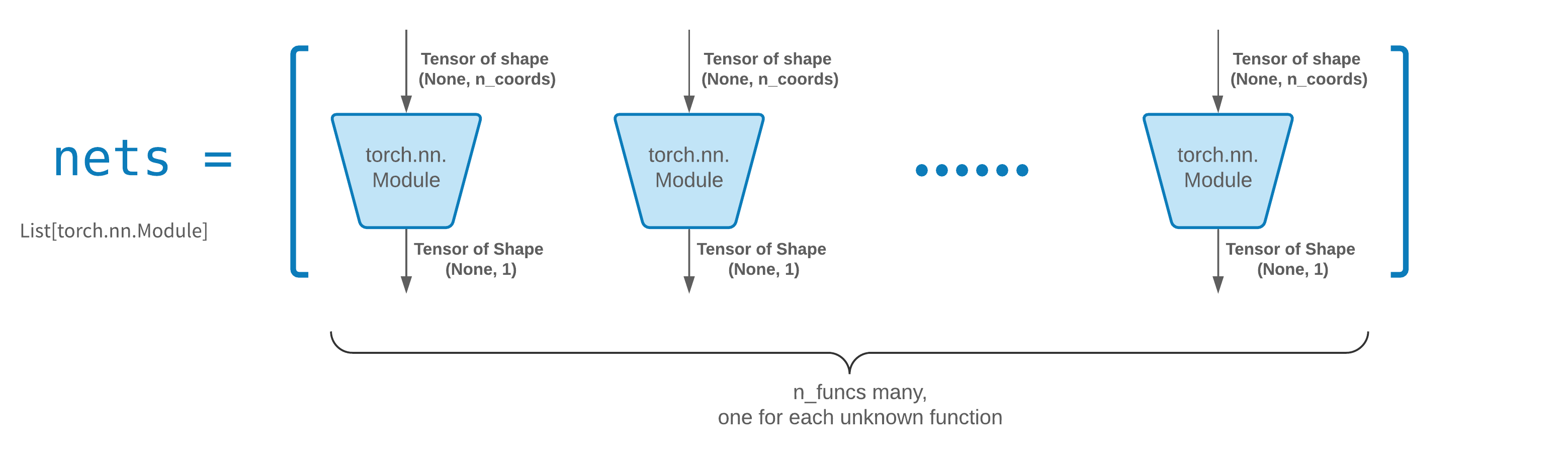
実際には、 neurodiffeqは上記のルールに従わないsingle_net機能がありますが、ここでは説明しません。
独自のネットワーク (別名モジュール) アーキテクチャの構築に関する PyTorch チュートリアルをお読みください。
転移学習は、 old_solver.nets (トーチ モジュールのリスト) をディスクにシリアル化し、ロードして新しいソルバーに渡すことで簡単に実行できます。
old_solver.fit(max_epochs=...)# ... `old_solver.nets` をディスク# にダンプします。 ディスクからネットワークをロードし、それらをいくつかの `loaded_nets` 変数に保存しますnew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
現在、ソルバーのネットワークやその他の内部変数を保存/ロードするためのラッパー関数に取り組んでいます。それまでの間、ネットワークの保存と読み込みに関する PyTorch チュートリアルを読むことができます。
Neurodiffeq では、ドメイン内の一連の点で評価される損失 (ODE/PDE 残差) を最小化することによってネットワークがトレーニングされます。ポイントは毎回ランダムに再サンプリングされます。サンプリングされたポイントの数、分布、および境界領域を制御するには、独自のトレーニング/検証generatorを指定できます。
from neodiffeq.generators import Generator1D# デフォルト t_min=0.0、t_max=1.0、method='uniform'、noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. .,noise_std=...)g2 = Generator1D(size=..., t_min=..., t_max=..., Method=..., Noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
以下に、 Generator1Dのサンプル ディストリビューションをいくつか示します。
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
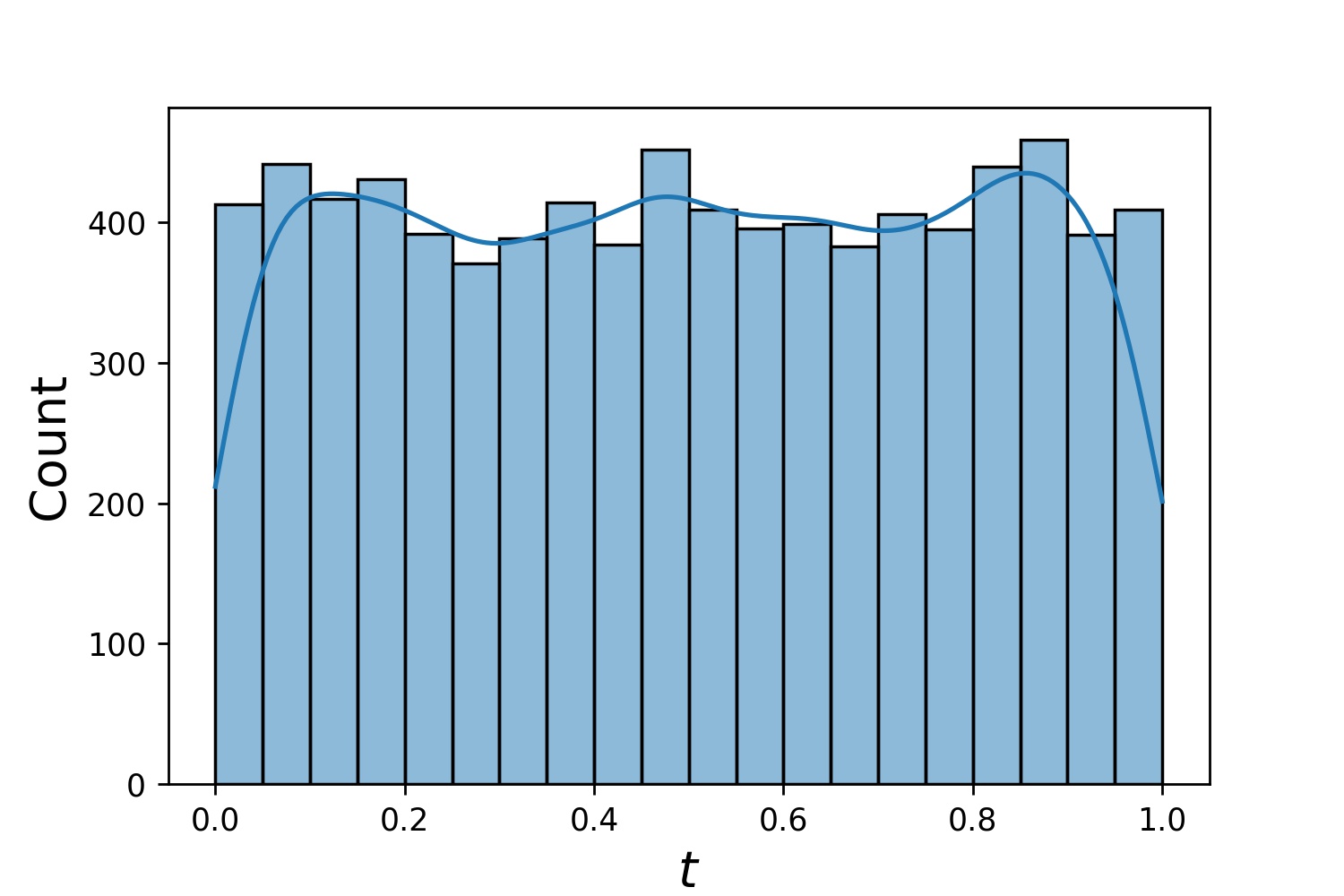 | 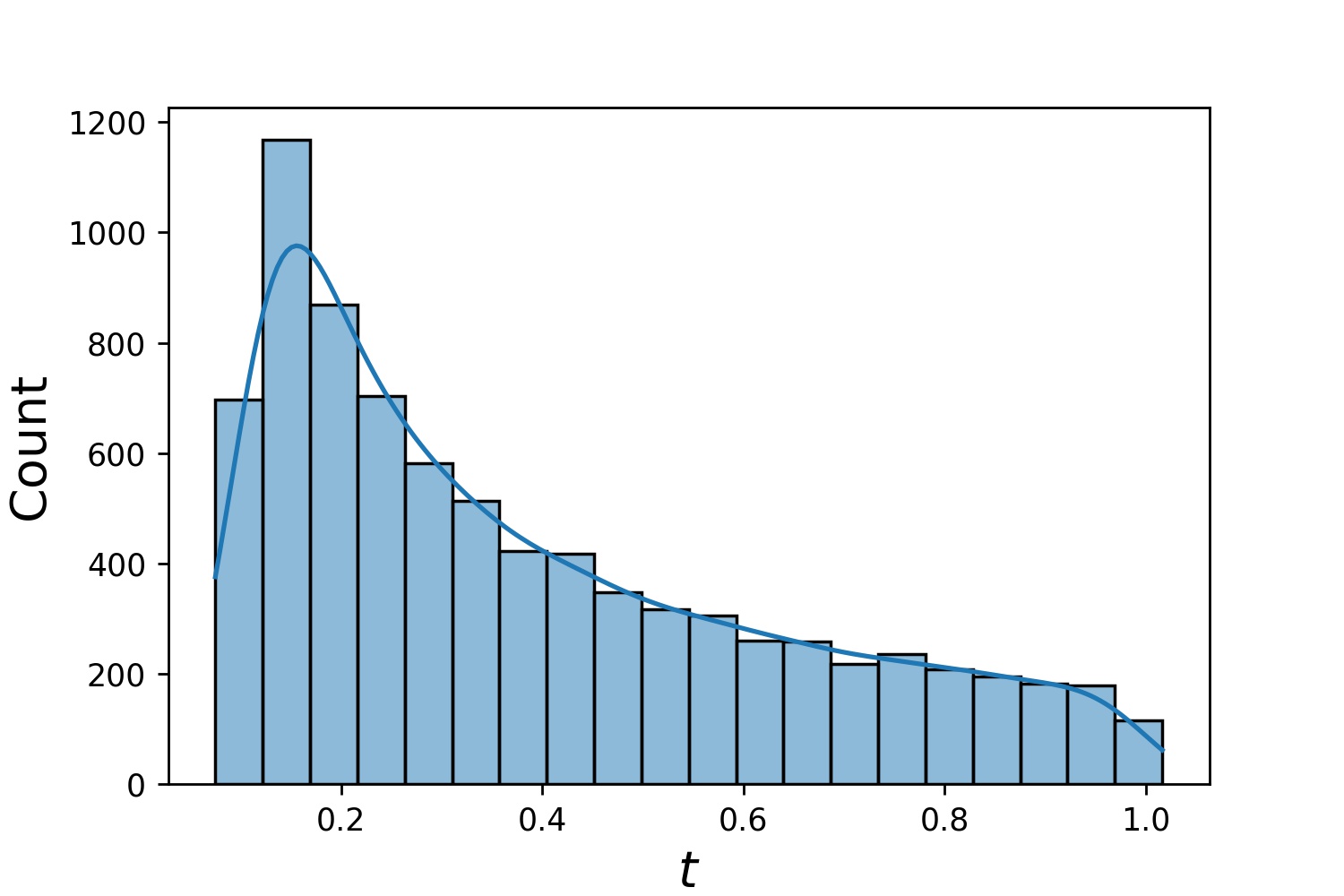 |
train_generatorとvalid_generator両方を指定した場合、 Solver1D(...)ではt_minとt_max省略できることに注意してください。実際、 t_min 、 t_max 、 train_generator 、 valid_generatorを一緒に渡しても、 t_minとt_max無視されます。
ジェネレーターのもう 1 つの優れた機能は、ジェネレーターを連結できることです。
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2) ))g = g1 + g2
ここで、 g g1とg2を組み合わせたサンプルを出力するジェネレーターになります。
g1 | g2 | g1 + g2 |
|---|---|---|
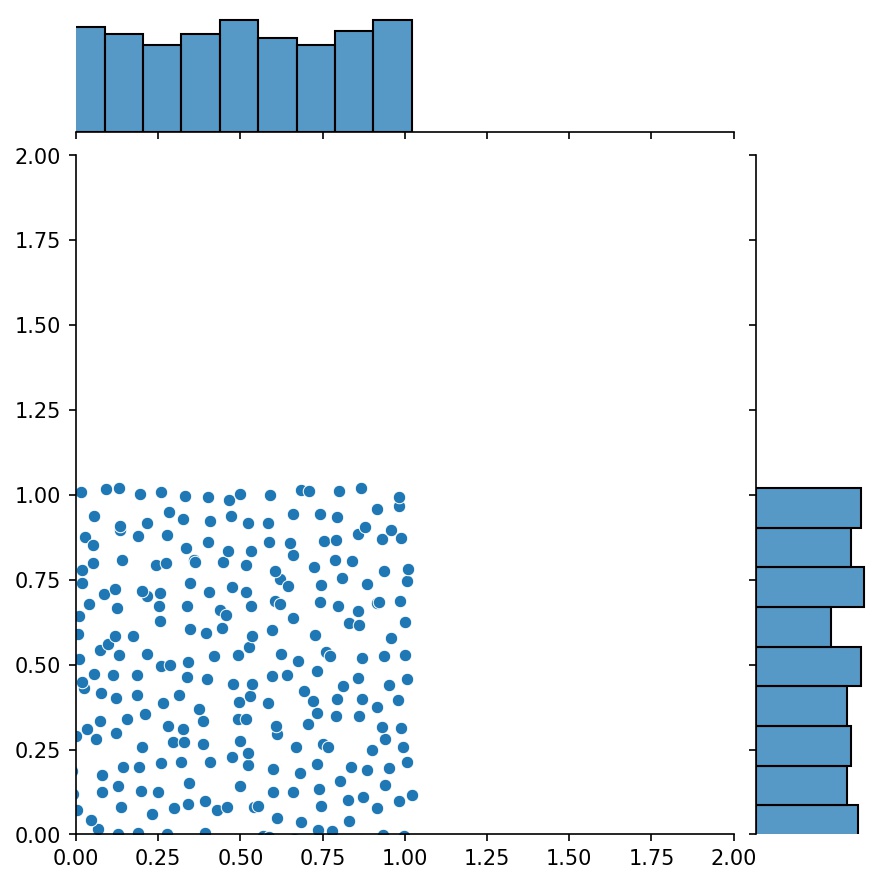 | 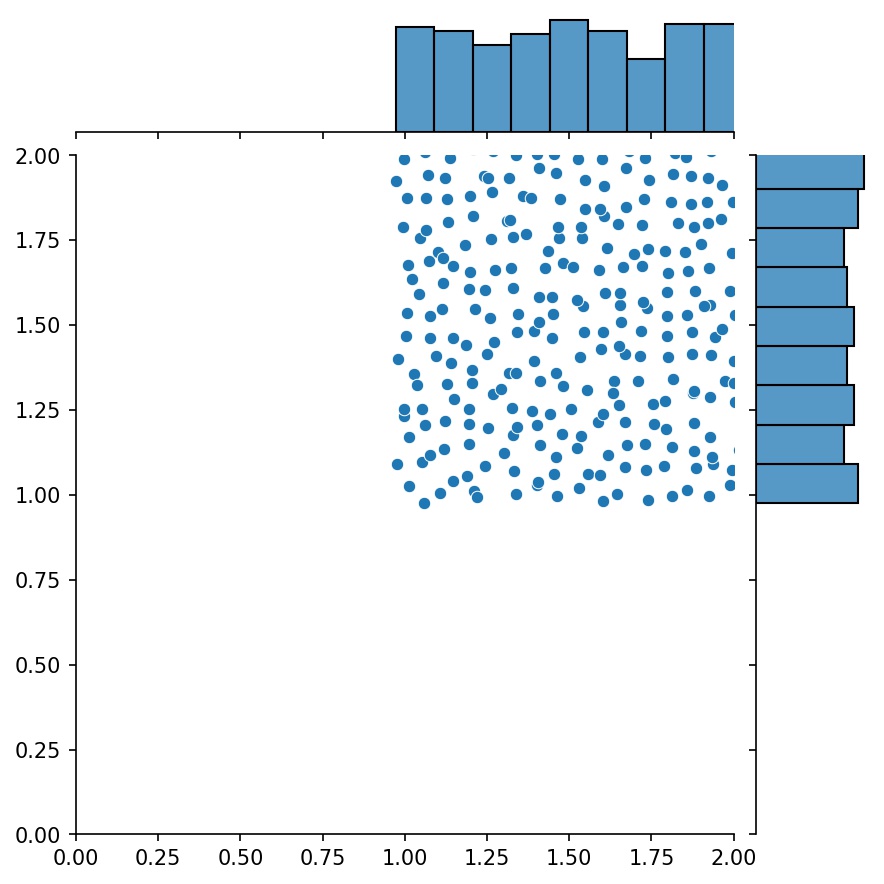 | 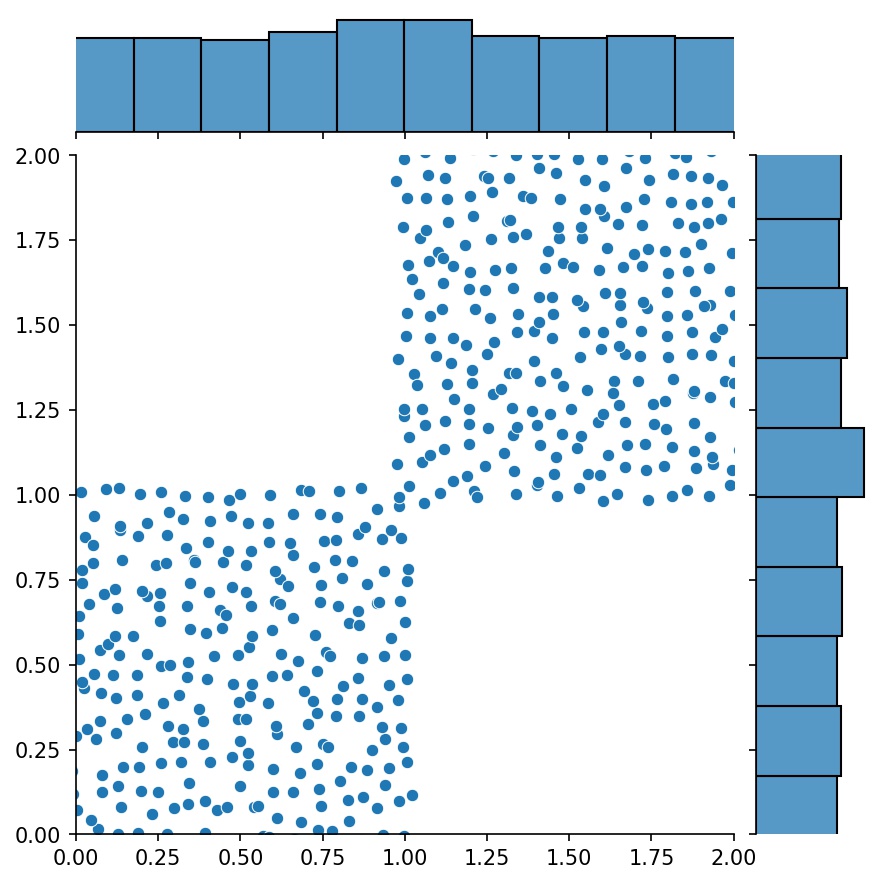 |
高次元で点をサンプリングするには、 Generator2D 、 Generator3Dなどを使用できます。でも別の方法もあります
g1 = Generator1D(1024, 2.0, 3.0, method='uniform')g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy',noise_std=0.001)g = g1 * g2
ここで、 g 2 次元の長方形(2,3) × (0.1,1)内に 1024 個の点を毎回生成するジェネレータになります。それらの x 座標は、 uniform戦略を使用して(2,3)から描画され、y 座標はlog-spaced-noisy戦略を使用して(0.1,1)から描画されます。
g1 | g2 | g1 * g2 |
|---|---|---|
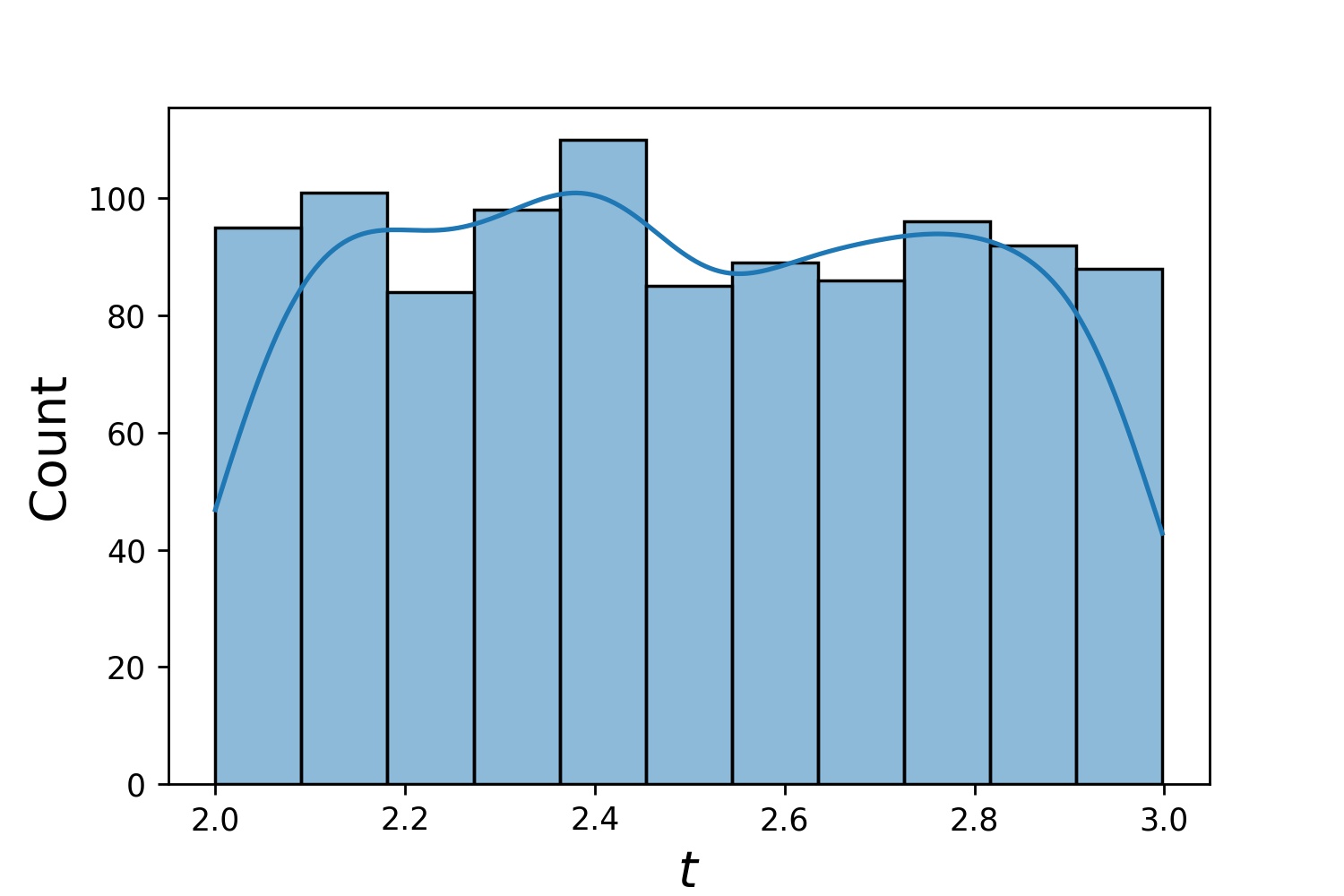 | 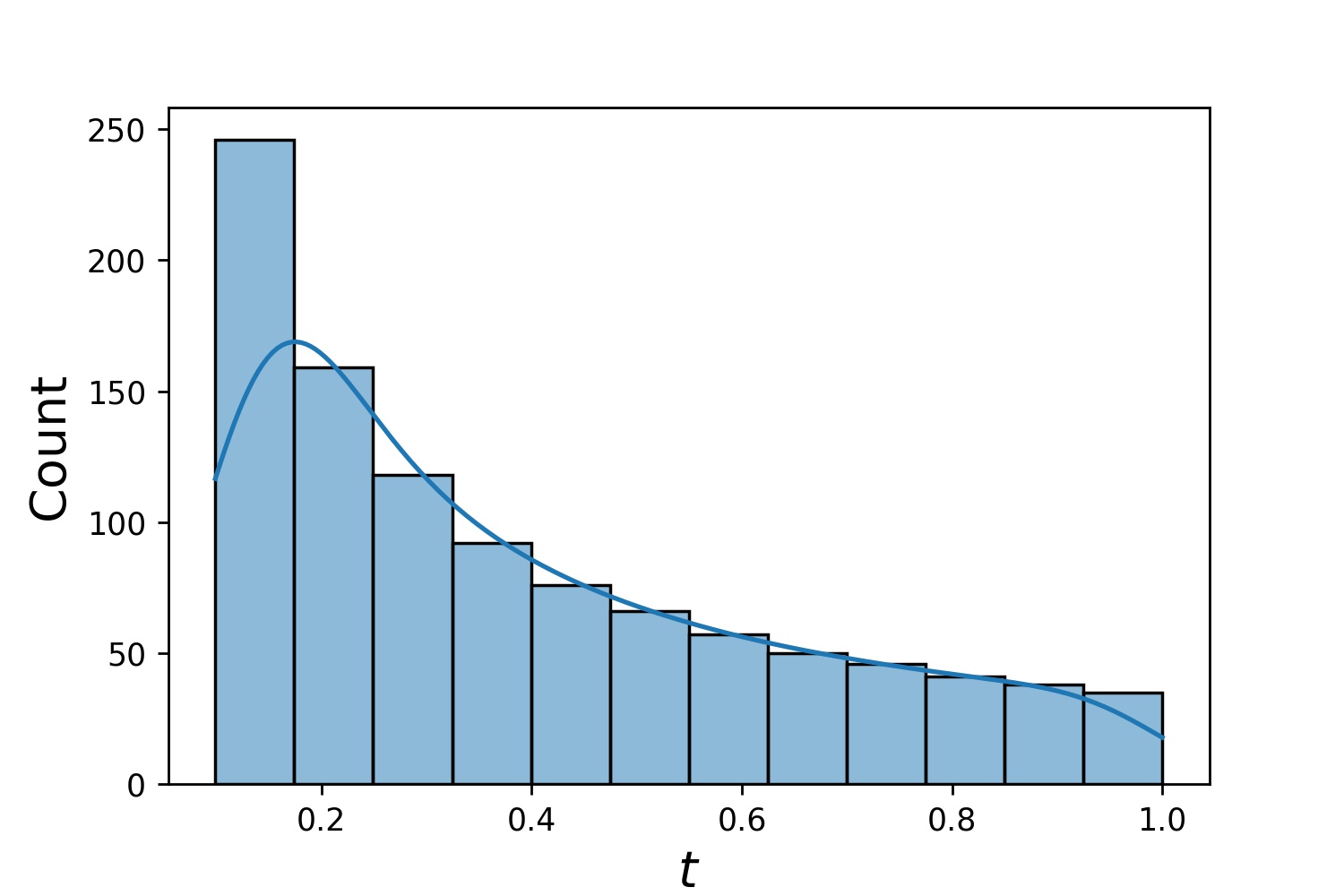 | 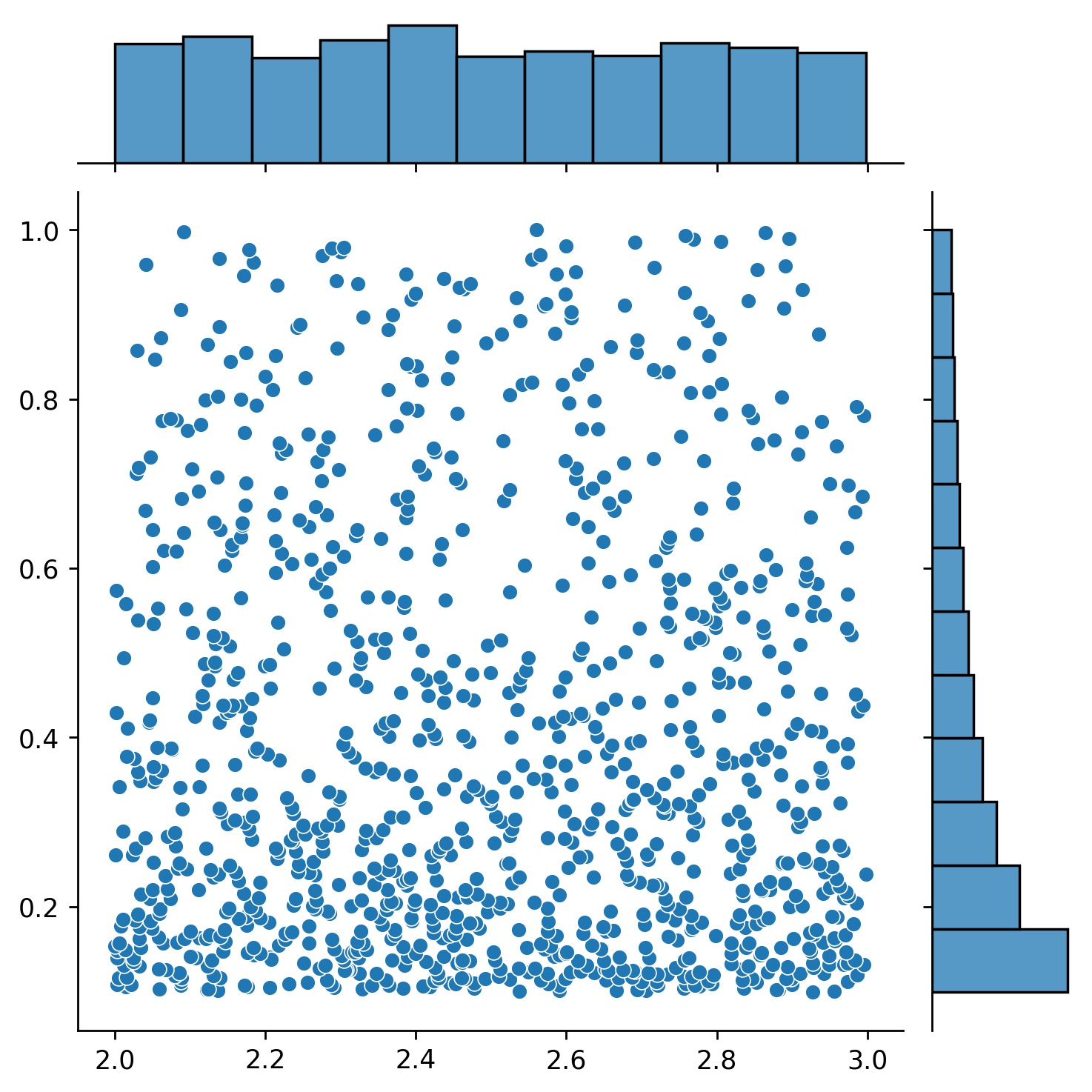 |
場合によっては、一連の方程式を一度に解くと面白いことがあります。たとえば、初期条件u(0) = U0の下で、 du/dt + λu = 0の形式の微分方程式を解きたい場合があります。すべてのλとU0をニューラル ネットワークへの入力として扱うことで、これを一度に解決したい場合があります。
そのような用途の 1 つは、反応速度が不明な化学反応です。異なる反応速度は異なる溶液に対応し、観察されたデータ ポイントと一致する溶液は 1 つだけです。最初に一連の解を求めてから、最適な反応速度 (別名方程式パラメーター) を決定することに興味があるかもしれません。 2 番目のステップは、逆問題として知られています。
neurodiffeq使用してこれを行う方法の例を次に示します。
方程式du/dt + λu = 0と初期条件u(0) = U0があるとします。ここで、 λとU0は未知の定数です。観測値t_obsとu_obsのセットもあります。まず、ソリューション バンドルを取得するために必要なBundleSolverとBundleIVPをインポートします。
from Neurodiffeq.conditions import BundleIVPfrom Neurodiffeq.solvers import BundleSolver1Dimport matplotlib.pyplot as pltimport numpy as npimport torchfrom Neurodiffeq import diff
入力tの定義域とパラメーターλおよびU0の定義域を決定します。パラメータの順序も決定する必要があります。つまり、どれを最初のパラメータにし、どれを 2 番目のパラメータにするかです。このデモの目的のために、最初のパラメータ (インデックス 0) としてλ選択し、2 番目のパラメータ (インデックス 1) としてU0選択します。パラメーターのインデックスを追跡することは非常に重要です。
T_MIN、T_MAX = 0、1LAMBDA_MIN、LAMBDA_MAX = 3、5 # 最初のパラメータ、インデックス = 0U0_MIN、U0_MAX = 0.2、0.6 # 2 番目のパラメータ、インデックス = 1
次に、 IVPとSolver1Dの代わりにBundleIVPとBundleSolver1D使用する点を除いて、通常どおりconditionsとsolver定義します。これら 2 つのインターフェイスは、 IVPおよびSolver1Dに非常に似ています。詳細については、API リファレンスを参照してください。
# 方程式パラメータは入力 (通常は時間座標と空間座標) の後に来ます。 diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# BundleIVP では、キーワード引数の名前は「u_0」でなければなりません。他のもの、たとえば `y0`、`u0` などを使用すると、機能しません。conditions = [BundleIVP(t_0=0, u_0=None,bundle_param_lookup={'u_0': 1}) # u_0 hasインデックス 1]ソルバー = BundleSolver1D(ode_system=diff_eq,conditions=条件,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ のインデックスは 0; u_0 のインデックスは 1theta_max=[LAMBDA_MAX, U0_MAX], # λ のインデックスは 1eq_param_index=(0,), # λ のみインデックス 0n_batches_valid=1 を持つ方程式パラメータ、
) λ方程式のパラメータであり、 U0初期条件のパラメータであるため、 diff_eqにλ 、条件にU0含める必要があります。パラメータが方程式と条件の両方に存在する場合は、両方の場所に含める必要があります。 BundleSovler1Dに渡されるconditionsのすべての要素は、パラメーターがない場合でも、 Bundle*条件である必要があります。
これで、通常どおりトレーニングして解を得ることができます。
solver.fit(max_epochs=1000)solution =solver.get_solution(best=True)
このソリューションでは、 t 、 λ 、 U0という 3 つの入力が必要です。すべての入力は同じ形状でなければなりません。たとえば、 λ=4およびU0=0.4を固定し、 t ∈ [0,1]に対して解uプロットすることに興味がある場合は、次のようにすることができます。
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = solution(t, lmd, u0, to_numpy=True)matplotlib.pyplot を pltplt としてインポート.plot(t, u)
バンドルされたsolutionを取得すると、観測されたデータ ポイント(t_i, u_i)に最もよく一致するパラメーターのセット(λ, U0)を見つけることができます。これは、単純な勾配降下法を使用して実現されます。次のおもちゃの例では、データ ポイントが 3 つだけu(0.2) = 0.273 、 u(0.5)=0.129 、およびu(0.8) = 0.0609であると仮定します。以下は古典的な PyTorch ワークフローです。
# 観測データ pointst_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# ランダムな初期化λ と U0 の関係。勾配を追跡しますlmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)# 勾配降下法を 10000 epochsfor _ in range(10000) で実行します:output = solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs) ))損失 = ((出力 - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, loss = {loss.item()}")単純。 Neurodiffeq をインポートすると、ライブラリはマシンで CUDA が利用可能かどうかを自動的に検出します。このライブラリは PyTorch に基づいているため、互換性のある GPU デバイスが見つかった場合は、デフォルトのテンソル タイプをtorch.cuda.DoubleTensorに設定します。
「カスタム ネットワークと転移学習」のセクションを参照してください。
標準的な PyTorch の方法。
「カスタム ネットワーク」の説明に従ってネットワークを構築します: nets = [FCNN(), FCN(), ...]
カスタム オプティマイザーをインスタンス化し、これらのネットワークのすべてのパラメーターをそれに渡します
パラメータ = [p for net in nets for p in net.parameters()] # すべてのネットワークのパラメータのリストMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
netsとoptimizer両方をソルバーに渡します: solver = Solver1D(..., nets=nets, optimizer=optimizer)
従来の数値手法 (FEM、FVM など) とは異なり、NN ベースのソリューションにはある程度のハイパーチューニングが必要です。このライブラリは、ハイパーパラメータのあらゆる組み合わせを試すための最大限の柔軟性を提供します。
別のネットワーク アーキテクチャを使用するには、カスタムのtorch.nn.Moduleを渡します。
別のオプティマイザーを使用するには、独自のオプティマイザーをsolver = Solver(..., optimizer=my_optim)に渡します。
別のサンプリング分布を使用するには、組み込みのジェネレーターを使用するか、独自のジェネレーターを最初から作成することができます。
別のサンプリング サイズを使用するには、ジェネレーターを調整するか、 solver = Solver(..., n_batches_train)変更します。
トレーニング中にハイパーパラメータを動的に変更するには、コールバック機能をチェックアウトしてください。
ReLU の 2 次導関数はまったく 0 であるため、活性化にはReLU使用しないでください。
PDE/ODE を無次元形式で再スケールし、できればすべてを[0,1]の範囲にします。 [0,1000000]のようなドメインを扱うと失敗する傾向があります。a ) PyTorch はモジュールの重みを比較的小さく初期化し、 b)ほとんどの活性化関数 (Sigmoid、Tanh、Swish など) は 0 付近で最も非線形になるためです。
PDE/ODE が複雑すぎる場合は、カリキュラム学習を試してみることを検討してください。より小さなドメインでネットワークのトレーニングを開始し、ドメイン全体がカバーされるまで徐々に拡張してください。
どなたでもこのプロジェクトに貢献していただけますようお願いいたします。
このリポジトリに貢献するときは、次のプロセスを考慮します。
問題を開いて、計画している変更について話し合います。
投稿ガイドラインを確認してください。
フォークされたリポジトリに変更を加え、インターフェイスに変更が加えられた場合は README.md を更新します。
プルリクエストを開きます。