우리의 새로운 데이터 세트인 PuzzleVQA는 단순한 추상 패턴을 이해하는 데 있어 다중 모드 LLM의 심각한 과제를 보여줍니다. 종이 | 웹사이트
다중 모드 추론을 위한 새롭고 도전적인 데이터 세트인 AlgoPuzzleVQA를 출시합니다! 곧 더 많은 다중 모드 퍼즐 데이터세트를 출시할 예정입니다. 계속 지켜봐 주시기 바랍니다! 종이 | 웹사이트
퍼즐을 중심으로 한 두 가지 새로운 VQA 데이터 세트의 출시를 발표하게 되어 기쁘게 생각합니다.
두 데이터 세트 모두에서 MLLM의 성능은 눈에 띄게 부족하며, 이는 다중 모달 추론 기능을 실질적으로 향상시켜야 한다는 절박한 필요성을 강조합니다.
대규모 다중 모드 모델은 다중 모드 이해 기능을 통합하여 대규모 언어 모델의 인상적인 기능을 확장합니다. 그러나 인간의 일반적인 지능과 추론 능력을 어떻게 모방할 수 있는지는 확실하지 않습니다. 패턴을 인식하고 개념을 추상화하는 것이 일반 지능의 핵심이므로 추상 패턴을 기반으로 한 퍼즐 모음인 PuzzleVQA를 소개합니다. 이 데이터 세트를 사용하여 색상, 숫자, 크기 및 모양을 포함한 기본 개념을 기반으로 하는 추상 패턴을 갖춘 대규모 다중 모드 모델을 평가합니다. 최첨단 대형 다중 모드 모델에 대한 실험을 통해 우리는 모델이 단순한 추상 패턴으로 일반화할 수 없다는 것을 발견했습니다. 특히 GPT-4V조차도 퍼즐의 절반 이상을 풀 수 없습니다. 대규모 다중 모드 모델의 추론 문제를 진단하기 위해 시각적 인식, 귀납적 추론 및 연역적 추론에 대한 지상 진실 추론 설명을 통해 모델을 점진적으로 안내합니다. 우리의 체계적인 분석에 따르면 GPT-4V의 주요 병목 현상은 약한 시각적 인식과 귀납적 추론 능력입니다. 이 작업을 통해 우리는 대규모 다중 모드 모델의 한계와 미래에 인간의 인지 과정을 더 잘 모방할 수 있는 방법을 밝힐 수 있기를 바랍니다.
PuzzleVQA는 여기와 Huggingface에서도 이용 가능합니다.
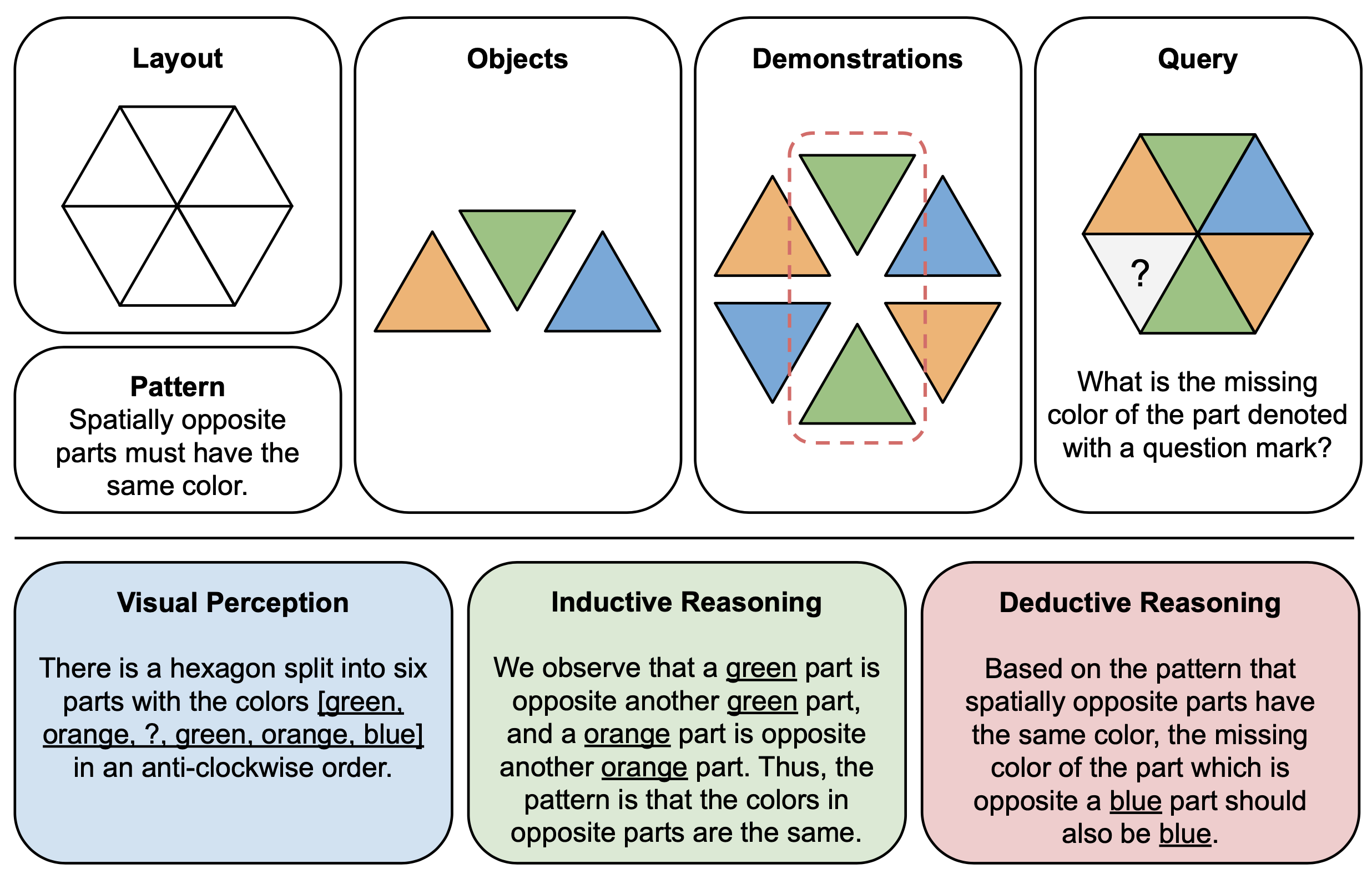
아래 그림은 PuzzleVQA의 색상 개념과 관련된 예시 질문과 GPT-4V의 오답을 보여줍니다. 일반적으로 해결 과정에서 관찰할 수 있는 세 단계는 시각적 인식(파란색), 귀납적 추론(녹색), 연역적 추론(빨간색)입니다. 여기서 시각적 인식이 불완전하여 연역적 추론에 오류가 발생했습니다.

아래 그림은 PuzzleVQA의 추상 퍼즐에 대한 구성 요소(상단)와 추론 설명(하단)의 예시를 보여줍니다. 각 퍼즐 인스턴스를 구성하기 위해 먼저 다중 모드 템플릿의 레이아웃과 패턴을 정의하고 기본 패턴을 보여주는 적절한 객체로 템플릿을 채웁니다. 해석 가능성을 위해 퍼즐을 해석하고 일반적인 해결 단계를 설명하기 위한 정답 추론 설명도 구성합니다.
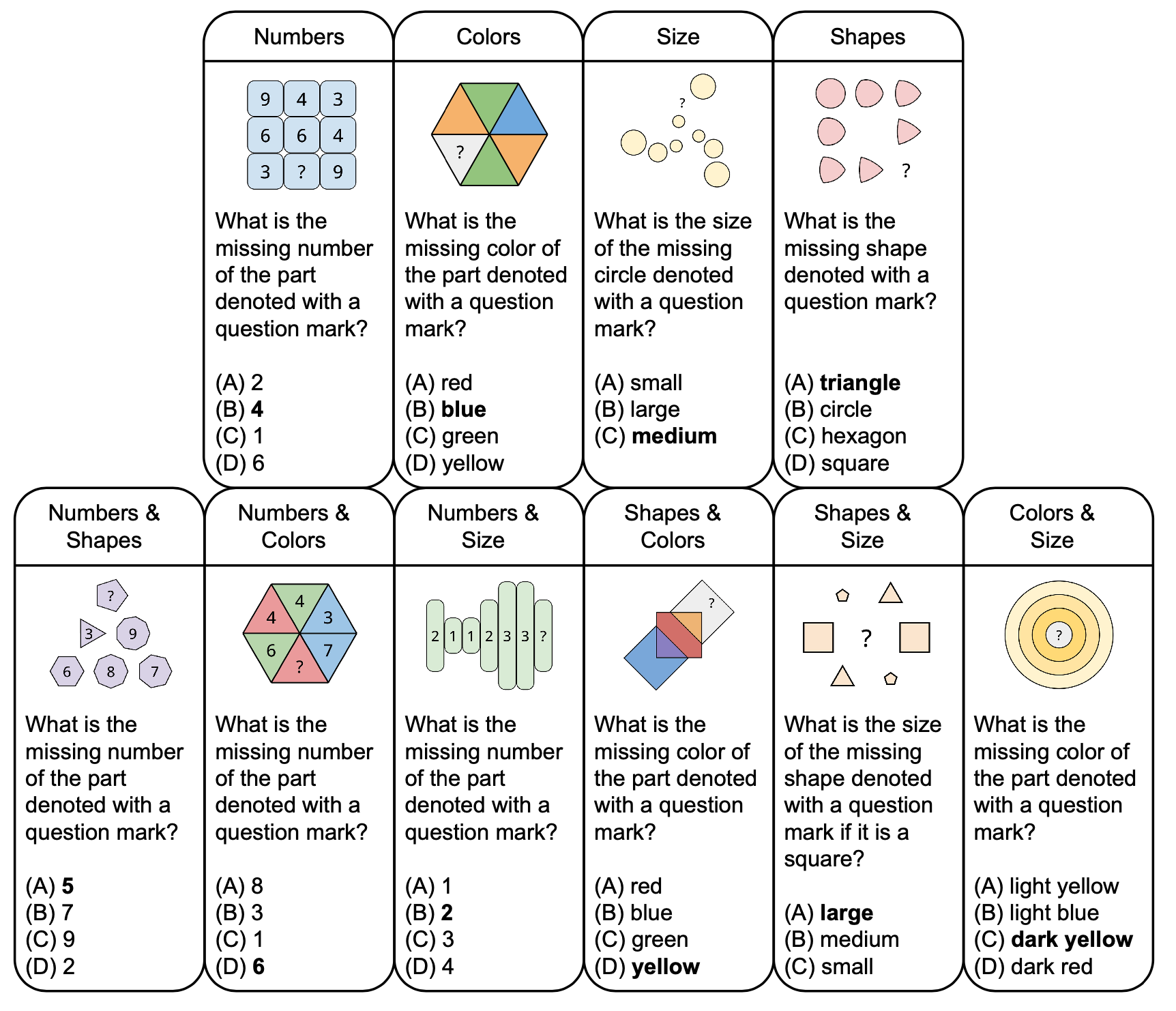
아래 그림은 색상, 크기 등 기본 개념을 기반으로 한 샘플 질문과 함께 PuzzleVQA의 추상 퍼즐 분류를 보여줍니다. 다양성을 높이기 위해 단일 컨셉과 이중 컨셉의 퍼즐을 모두 디자인합니다.
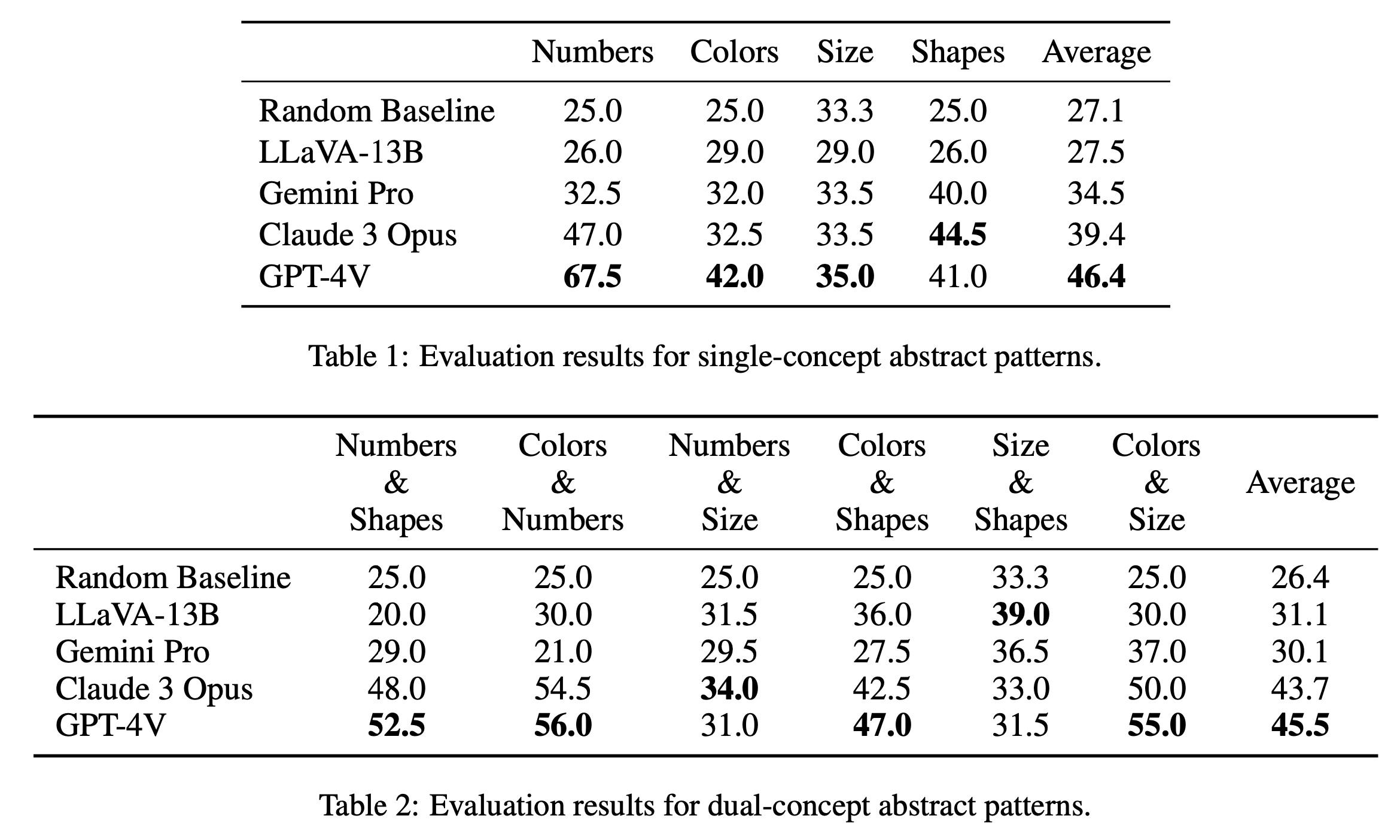
단일 개념 퍼즐과 이중 개념 퍼즐에 대한 주요 평가 결과를 각각 표 1과 표 2에 보고합니다. 표 1과 같이 단일 개념 퍼즐에 대한 평가 결과는 오픈 소스 모델과 폐쇄 소스 모델 간의 성능에서 눈에 띄는 차이를 보여줍니다. GPT-4V는 평균 46.4점으로 가장 높은 점수를 받아 숫자, 색상, 크기 등 단일 개념 퍼즐에서 뛰어난 추상 패턴 추론을 보여줍니다. 특히 "숫자" 카테고리에서 67.5점으로 다른 모델을 훨씬 능가하며 이는 수학 추론 작업에서의 이점 때문일 수 있습니다(Yang et al., 2023). Claude 3 Opus는 전체 평균 39.4점으로 뒤를 잇고 있으며, 최고 점수 44.5점으로 "Shapes" 카테고리에서 강점을 보여줍니다. Gemini Pro 및 LLaVA-13B를 포함한 다른 모델은 각각 평균 34.5 및 27.5로 뒤처져 여러 범주에서 무작위 기준선과 유사한 성능을 발휘합니다.
이중개념 퍼즐 평가에서는 Table 2와 같이 GPT-4V가 평균 45.5점으로 가장 높은 점수를 받아 다시 한 번 두각을 나타냈다. 특히 "색상 및 숫자"와 "색상 및 크기"와 같은 카테고리에서 각각 56.0점과 55.0점을 받아 좋은 성적을 거두었습니다. 클로드 3 오푸스(Claude 3 Opus)가 평균 43.7점으로 바짝 뒤쫓고 있으며, '숫자 및 크기(Numbers & Size)' 부문에서 최고점 34.0으로 강력한 성능을 보였다. 흥미롭게도 LLaVA-13B는 전체 평균이 31.1로 낮음에도 불구하고 "크기 및 모양" 범주에서 39.0으로 가장 높은 점수를 받았습니다. 반면에 Gemini Pro는 카테고리 전체에서 더 균형 잡힌 성능을 보이지만 전체 평균은 30.1로 약간 낮습니다. 전반적으로 우리는 모델이 단일 개념 및 이중 개념 패턴에 대해 평균적으로 유사하게 수행된다는 것을 발견했습니다. 이는 색상 및 숫자와 같은 여러 개념을 함께 연결할 수 있음을 시사합니다.
@misc{chia2024puzzlevqa,
title={PuzzleVQA: Diagnosing Multimodal Reasoning Challenges of Language Models with Abstract Visual Patterns},
author={Yew Ken Chia and Vernon Toh Yan Han and Deepanway Ghosal and Lidong Bing and Soujanya Poria},
year={2024},
eprint={2403.13315},
archivePrefix={arXiv},
primaryClass={cs.CV}
}
우리는 시각적 질문 답변의 맥락 내에서 구성된 다중 모드 퍼즐 해결의 새로운 작업을 소개합니다. 우리는 시각적 이해, 언어 이해 및 복잡한 알고리즘 추론이 모두 필요한 알고리즘 퍼즐을 풀 때 다중 모달 언어 모델의 기능에 도전하고 평가하기 위해 설계된 새로운 데이터 세트인 AlgoPuzzleVQA를 제시합니다. 우리는 부울 논리, 조합론, 그래프 이론, 최적화, 검색 등과 같은 다양한 수학적 및 알고리즘 주제를 포괄하는 퍼즐을 만들어 시각적 데이터 해석과 알고리즘 문제 해결 기술 간의 격차를 평가합니다. 데이터 세트는 사람이 작성한 코드에서 자동으로 생성됩니다. 우리의 모든 퍼즐에는 사람이 지루하게 계산하지 않고도 알고리즘을 통해 찾을 수 있는 정확한 답이 있습니다. 이는 추론 복잡성과 데이터 세트 크기 측면에서 데이터 세트를 임의로 확장할 수 있도록 보장합니다. 우리의 조사에 따르면 GPT4V 및 Gemini와 같은 LLM(대형 언어 모델)은 퍼즐 해결 작업에서 제한된 성능을 보이는 것으로 나타났습니다. 우리는 상당수의 퍼즐에 대한 객관식 질문 답변 설정에서 그들의 성과가 거의 무작위라는 것을 발견했습니다. 연구 결과는 복잡한 추론 문제를 해결하기 위해 시각적, 언어 및 알고리즘 지식을 통합하는 과제를 강조합니다.
PuzzleVQA는 여기와 Huggingface에서도 이용 가능합니다.
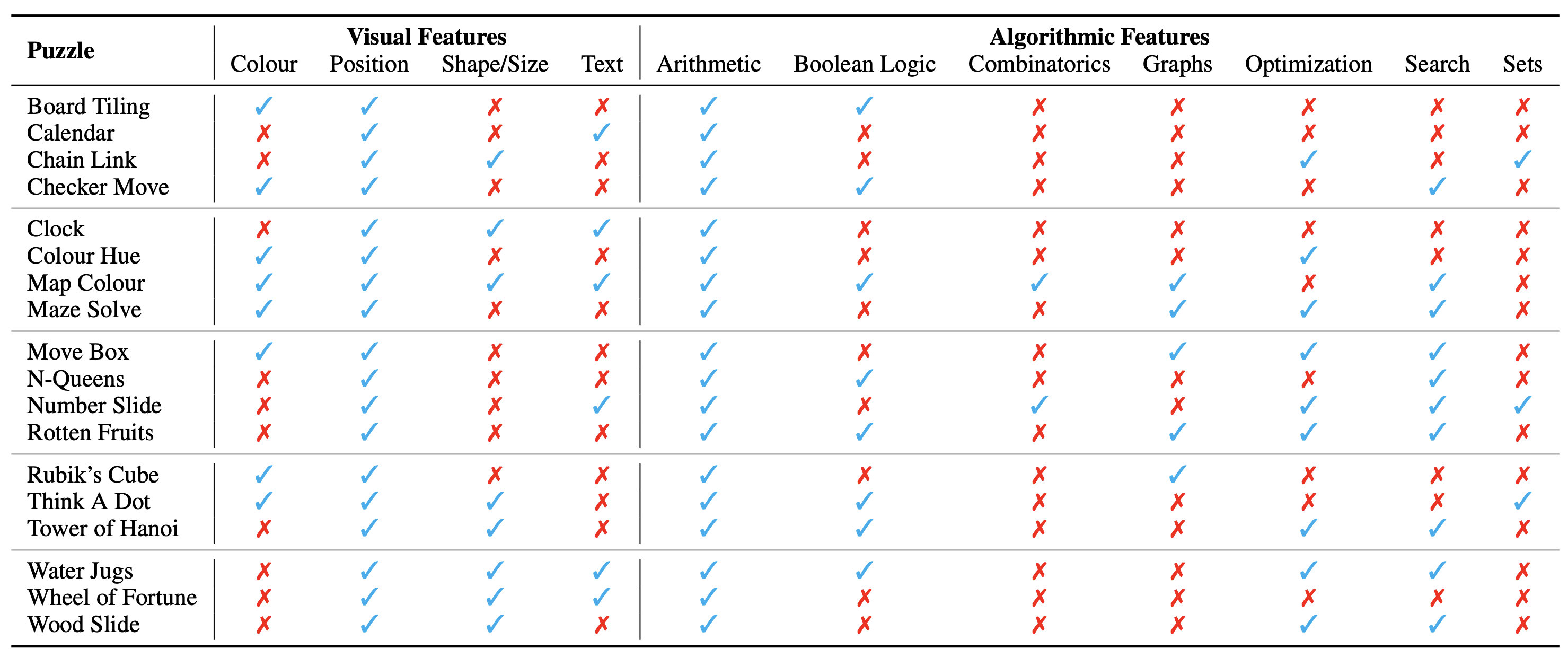
퍼즐/문제의 구성은 시각적 맥락을 구성하는 이미지로 표시됩니다. 우리는 퍼즐의 성격에 영향을 미치는 시각적 맥락의 다음과 같은 기본 측면을 식별합니다.

우리는 또한 퍼즐을 해결하는 데, 즉 퍼즐 인스턴스에 대한 질문에 답하는 데 필요한 알고리즘 개념을 식별합니다. 그것들은 다음과 같습니다:

대부분의 퍼즐에 대한 답을 도출하려면 두 개 이상의 범주를 사용해야 하므로 알고리즘 범주는 상호 배타적이지 않습니다.
데이터 세트는 여기에서 다음 형식으로 제공됩니다. 우리는 다양한 알고리즘과 수학 주제에 걸쳐 총 18개의 퍼즐을 만들었습니다. 이러한 퍼즐 중 다수는 다양한 레크리에이션 또는 학업 환경에서 인기가 있습니다.
전체적으로 18개의 서로 다른 퍼즐에서 1800개의 인스턴스가 있습니다. 이러한 인스턴스는 퍼즐의 다양한 테스트 사례 와 유사합니다. 즉, 입력 조합, 초기 및 목표 상태 등이 다릅니다. 모든 인스턴스를 안정적으로 해결하려면 사용할 정확한 알고리즘을 찾아 이를 정확하게 적용해야 합니다. 이는 광범위한 테스트 사례를 통해 특정 작업을 해결하는 것을 목표로 하는 컴퓨터 프로그램의 정확성을 검증하는 방법과 유사합니다.
현재 우리는 전체 데이터 세트를 평가 전용 벤치마크로 간주합니다. 모든 퍼즐의 자세한 예가 여기에 표시됩니다.
데이터 세트 생성에 대한 지침은 여기에서 찾을 수 있습니다. 인스턴스 수와 퍼즐의 난이도는 원하는 크기나 레벨에 맞게 임의로 조정할 수 있습니다.
퍼즐의 존재론적 분류는 다음과 같습니다.
실험 설정과 스크립트는 AlgoPuzzleVQA 디렉터리에서 찾을 수 있습니다.
우리의 작업이 유용하다고 생각되면 다음 기사를 인용해 보십시오.
@article { ghosal2024algopuzzlevqa ,
title = { Are Language Models Puzzle Prodigies? Algorithmic Puzzles Unveil Serious Challenges in Multimodal Reasoning } ,
author = { Ghosal, Deepanway and Han, Vernon Toh Yan and Chia, Yew Ken and and Poria, Soujanya } ,
journal = { arXiv preprint arXiv:2403.03864 } ,
year = { 2024 }
}