greta.gam: mgcv를 사용하는 greta의 일반화된 추가 모델

greta.gam을 사용하면 mgcv의 평활 함수 및 공식 구문을 사용하여 greta 모델에 사용할 평활 용어를 정의할 수 있습니다. 그런 다음 모델을 완성할 가능성을 직접 정의하고 MCMC를 통해 적합화할 수 있습니다.

이 작업이 진행 중입니다!

예

다음은 mgcv ?gam 도움말 파일에서 가져온 간단한 예입니다.

mgcv 에서 :

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

이제 greta 에 동일한 모델을 적용합니다.

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )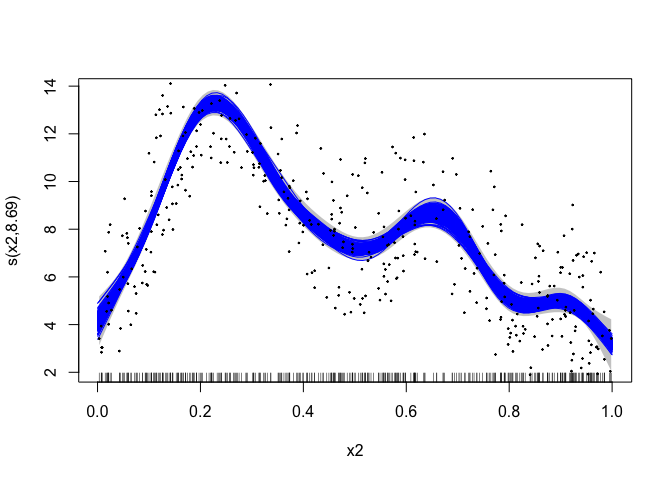

간략한 기술 세부정보

greta.gam mgcv 의 jagam (Wood, 2016) 루틴에서 몇 가지 트릭을 사용하여 작업을 수행합니다. 내부 작업에 관심이 있는 분들을 위한 간략한 세부 정보는 다음과 같습니다.

GAM의 베이지안 해석

GAM은 베이지안 해석을 사용하는 모델입니다("빈도주의" 방법을 사용하여 피팅한 경우에도 마찬가지). 더 부드러운 페널티 행렬을 베이지안 무작위 효과 모델의 사전 정밀도 행렬로 생각할 수 있습니다. 설계 행렬은 빈도주의 사례와 동일하게 구성됩니다. 이에 대한 자세한 배경은 Miller(2021)를 참조하세요.

페널티 매트릭스

GAM의 베이지안 해석에는 약간의 어려움이 있습니다. 순진한 형태에서 사전은 페널티의 영공간(1D 경우에는 일반적으로 선형 항)으로 부적절합니다. 적절한 사전확률을 얻기 위해 Marra & Wood(2011)에서 사용된 "트릭" 중 하나를 사용할 수 있습니다. 즉, 부적절한 사전확률로 이어지는 페널티 부분에 페널티를 적용하는 것입니다. 우리는 jagam 이 제공한 옵션을 선택하고 이러한 항에 대한 추가 페널티 행렬을 만듭니다(페널티 행렬의 고유 분해에서; Marra & Wood, 2011 참조).