홈 | 설치 | 문서 | 튜토리얼 | 개발자
Rodeo 는 확률 수치를 사용하여 상미분 방정식(ODE)을 푸는 빠른 Python 라이브러리입니다. 즉, 대부분의 ODE 솔버(예: 오일러 방법)는 단계 크기의 그리드에서 ODE에 대한 결정론적 근사를 생성합니다.
로데오는 많은 확률적 솔버에 공통적인 비선형 베이지안 필터링 패러다임에 대한 가볍고 확장 가능한 근사값 제품군을 제공합니다(Tronarp et al(2018)). 이는 먼저 ODE 솔루션에 가우스 프로세스를 배치하고 솔버가 그리드를 통과할 때 이를 순차적으로 업데이트하는 것으로 시작됩니다. 로데오는 적시 컴파일 및 자동 미분을 허용하는 jax를 기반으로 구축되었습니다. jax 의 API는 numpy 의 API와 거의 동일합니다.
Rodeo는 두 가지 주요 도구를 제공합니다. 하나는 ODE 솔루션을 근사화하는 도구이고 다른 하나는 매개변수 추론을 위한 도구입니다. 전자의 경우 다음을 제공합니다.
solve : 비선형 베이지안 필터링 패러다임을 사용하는 확률론적 ODE 솔버 구현.후자의 경우 우도 근사 방법을 제공합니다.
basic : 기본 우도 근사 방법 구현(자세한 내용은 Wu 및 Lysy(2023)에서 확인할 수 있음)fenrir : Fenrir 구현(Tronarp et al(2022)).marginal_mcmc : Chkrebtii 방법의 MCMC 구현(Chkrebtii et al(2016)).dalton : 데이터 적응형 ODE 우도 근사 구현(Wu 및 Lysy(2023)).사용법에 대한 자세한 예는 문서 섹션에서 찾을 수 있습니다. 이것은 jax 전용 버전의 Rodeo 입니다. 다양한 다른 백엔드를 사용하는 레거시 버전은 여기를 참조하세요.
GitHub에서 저장소를 다운로드한 후 setup.cfg 스크립트를 사용하여 설치합니다.
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . 다음 예제에 대한 렌더링된 문서를 보려면 먼저 문서를 읽으십시오.
간단한 ODE 문제 해결에 대한 빠른 시작 튜토리얼입니다.
고차 ODE를 푸는 예입니다.
어려운 혼돈 ODE를 해결하는 예입니다.
라플라스 근사를 사용하는 매개변수 추론 문제의 예입니다.
이 연습에서는 확률적 솔버를 사용하여 ODE를 해결하는 방법과 매개변수 추론을 수행하는 방법을 모두 보여줍니다. 먼저 ODE를 풀기 위한 설정을 설명하겠습니다. 이를 위해 다음과 같은 1차 ODE 예제( FitzHugh-Nagumo 모델)를 고려해 보겠습니다.
해결책은 어디에
(Wu and Lysy (2023))의 표기법에 따르면,
~을 위한
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) 솔버의 솔루션을 scipy 라이브러리의 odeint 제공하는 결정적 솔루션과 비교합니다.
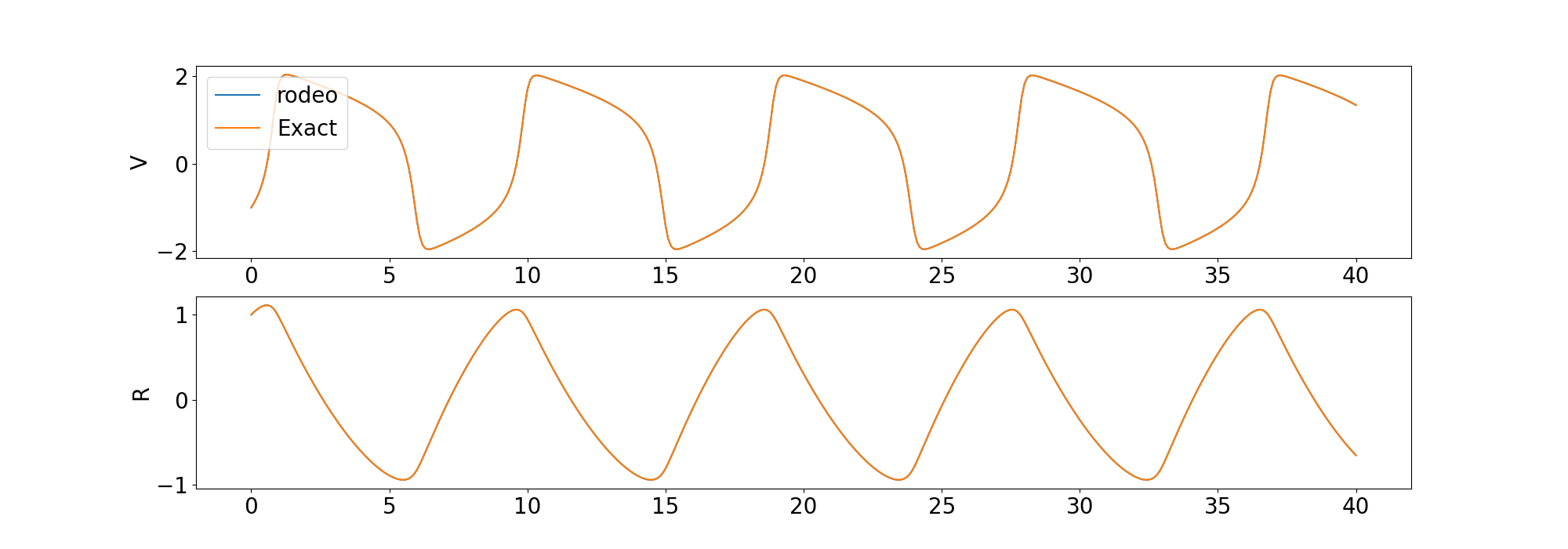
또한 고차 ODE와 카오스 ODE를 푸는 예제도 포함되어 있습니다.
이제 매개변수 추론 문제로 넘어갑니다. 로데오에는 설명 섹션에 요약된 몇 가지 우도 근사 방법이 포함되어 있습니다. 여기서는 basic 우도 근사법을 사용하겠습니다. 관측치가 모델을 통해 시뮬레이션된다고 가정합니다.
어디 basic 우도 근사를 구성할 수 있습니다.
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) 사용법을 설명하기 위한 기본 예제입니다. 우리는 fenrir , marginal_mcmc 및 dalton 과 같은 우도 근사에 솔루션 불확실성을 전파하는 보다 정교한 우도 근사를 제안합니다. 자세한 내용은 매개변수 추론 튜토리얼을 참조하세요.
다음은 /examples/ 의 로데오 에서 발견된 다양한 우도 근사에 의해 생성된 일부 결과입니다.
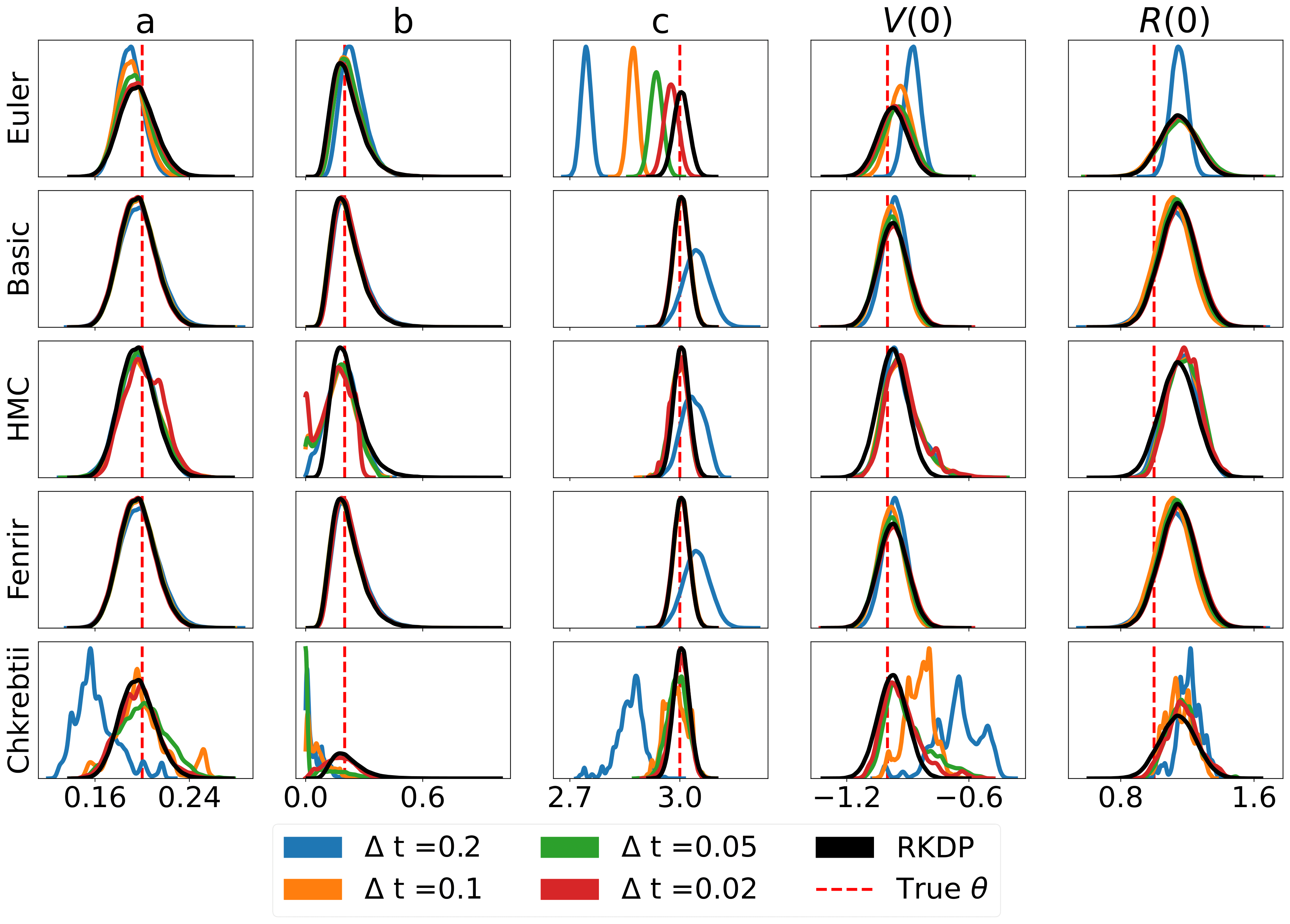
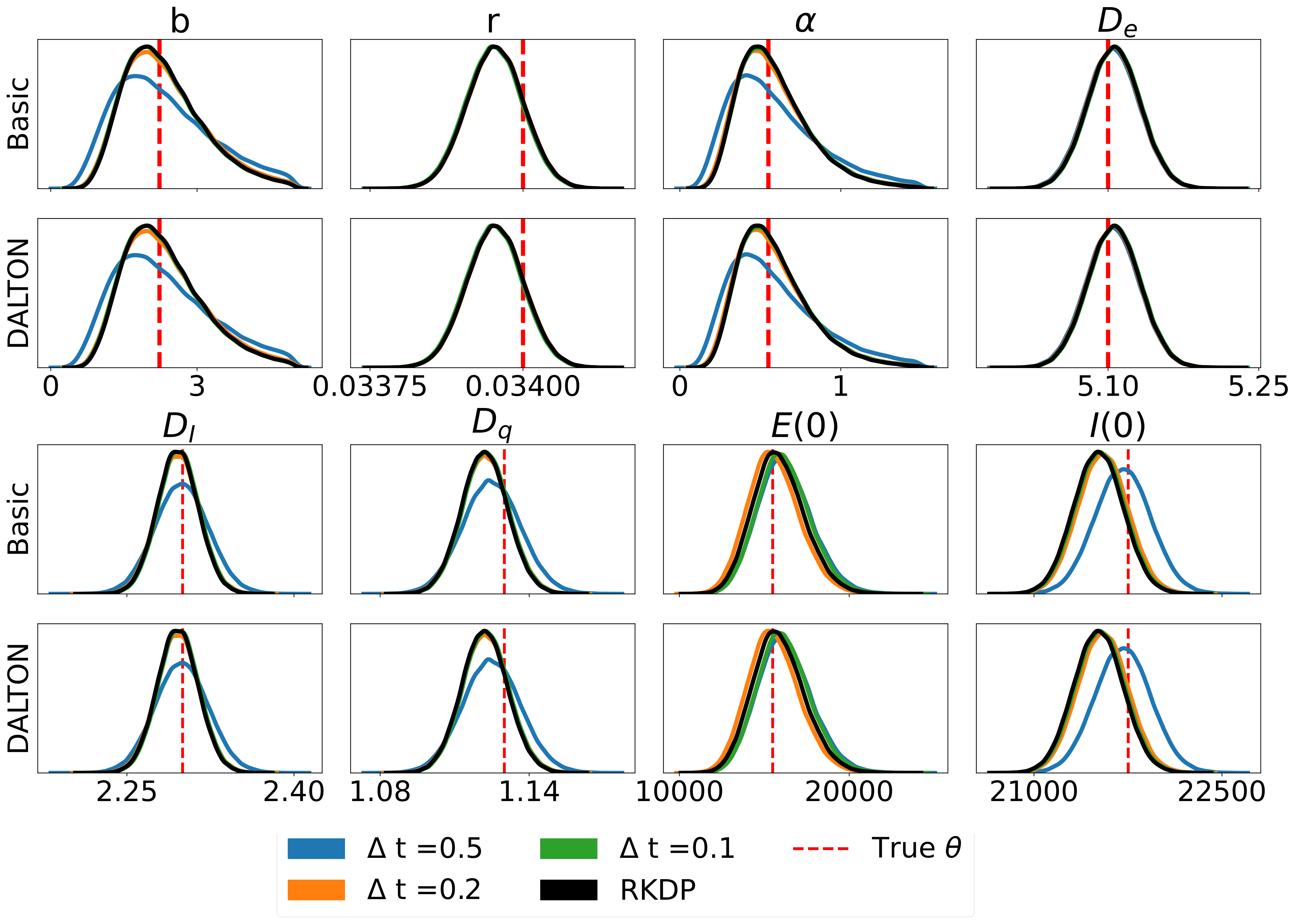
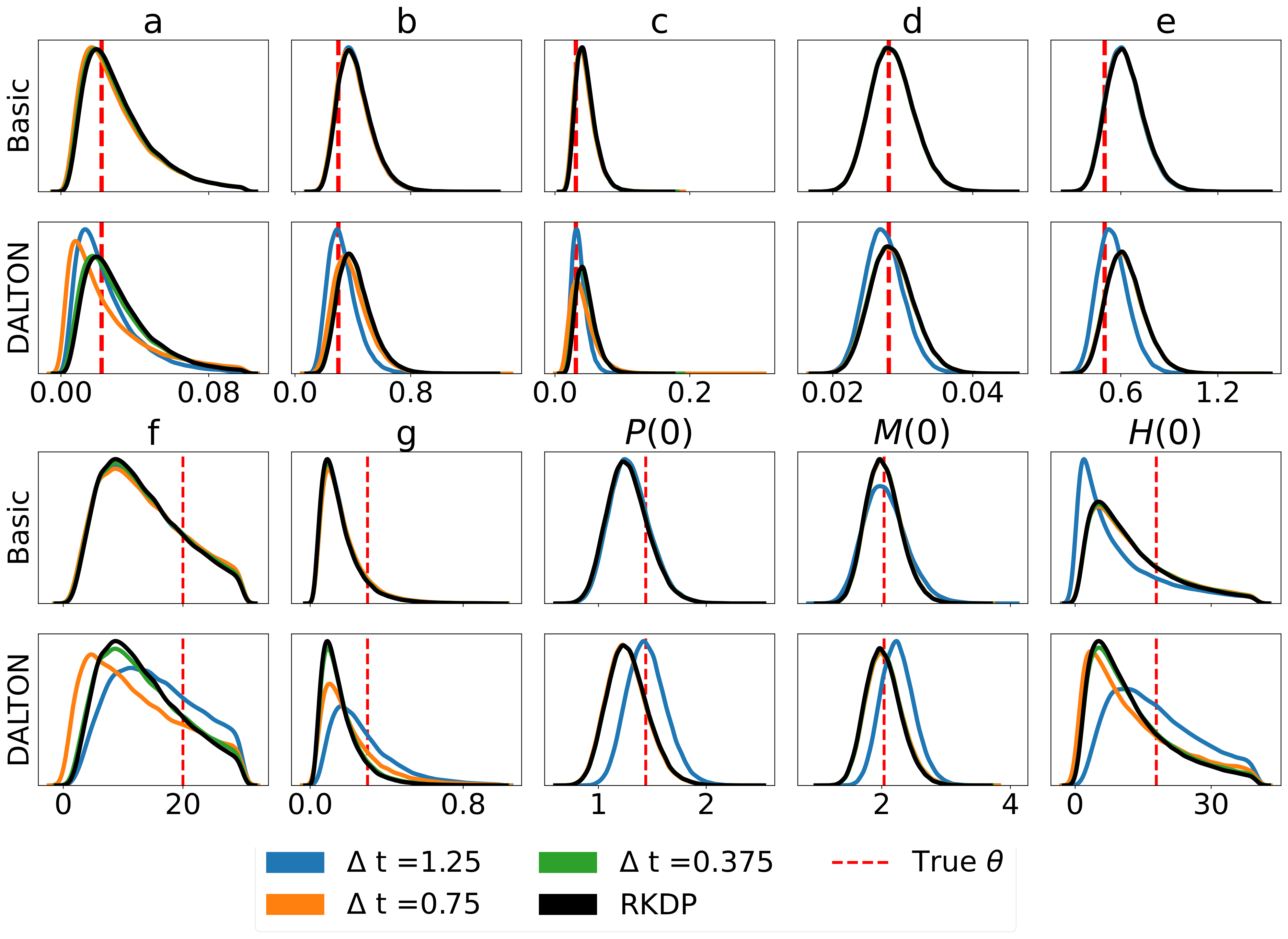
단위 테스트는 다음 명령을 통해 실행할 수 있습니다.
cd tests
python -m unittest discover -v 또는 tox 를 설치한 다음 rodeo 내에서 명령줄 tox 입력하세요.
HTML 문서는 루트 폴더에서 컴파일할 수 있습니다.
pip install .[docs]
cd docs
make html 그러면 docs/build 에 문서가 생성됩니다.