neurodiffeq

신경차이

소환

@article{chen2020neurodiffeq,
  title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
  author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
  journal={Journal of Open Source Software},
  volume={5},
  number={46},
  pages={1931},
  year={2020}
}

---

Neurodiffeq가 솔루션 번들을 지원하고 역 문제를 해결하는 데 사용할 수 있다는 것을 알고 계셨습니까? 여기를 참조하세요!

? 이미 Neurodiffeq에 대해 잘 알고 계시나요? ? FAQ로 이동하세요.

---

소개

neurodiffeq 는 신경망을 사용하여 미분 방정식을 풀기 위한 패키지입니다. 미분방정식은 일부 함수와 그 파생물을 연관시키는 방정식입니다. 그들은 다양한 과학 및 공학 영역에서 나타납니다. 전통적으로 이러한 문제는 수치적 방법(예: 유한 차분, 유한 요소)을 통해 해결될 수 있습니다. 이러한 방법은 효과적이고 적절하지만 표현 가능성은 기능 표현에 따라 제한됩니다. 연속적이고 미분 가능한 미분 방정식의 해를 계산할 수 있다면 흥미로울 것입니다.

범용 함수 근사기로서 인공 신경망은 특정 초기/경계 조건을 사용하여 상미분 방정식(ODE) 및 편미분 방정식(PDE)을 풀 수 있는 잠재력을 갖는 것으로 나타났습니다. neurodiffeq 의 목적은 소프트웨어가 광범위한 사용자 정의 문제를 처리할 수 있을 만큼 유연해질 수 있도록 ANN을 사용하여 미분 방정식을 푸는 기존 기술을 구현하는 것입니다.

설치

핍 사용

대부분의 표준 라이브러리와 마찬가지로 neurodiffeq PyPI에서 호스팅됩니다. 최신 안정 릴리스를 설치하려면,

 pip install -U Neurodiffeq # '-U'는 최신 버전으로 업데이트함을 의미합니다.

수동으로

또는 라이브러리를 수동으로 설치하여 새로운 기능에 조기에 액세스할 수 있습니다. 이는 라이브러리에 기여하려는 개발자에게 권장되는 방법입니다.

 git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd Neurodiffeq && pip install -r 요구 사항
핍 설치 .  # 라이브러리를 변경하려면 `pip install -e .`를 사용하세요. pytest 테스트/ # 테스트를 실행합니다. 선택 과목.

시작하기

어떤 질문이라도 기꺼이 도와드리겠습니다. 그동안 FAQ를 확인해 보세요.

neurodiffeq 의 전체 튜토리얼과 문서를 보려면 공식 문서를 확인하세요.

문서 외에도 최근 슬라이드가 포함된 간단한 연습 데모 비디오를 만들었습니다.

사용 예

수입품

 Neurodiffeq에서 diff 가져오기 Neurodiffeq.solvers 가져오기 Solver1D, Solver2D에서 Neurodiffeq.condition 가져오기 IVP, DirichletBVP2D에서 Neurodiffeq.networks 가져오기 FCNN, SinActv

ODE 시스템 예

여기서는 Lotka-Volterra 방정식으로 알려진 두 ODE의 비선형 시스템을 풉니다. 두 개의 미지 함수( u 및 v )와 단일 독립 변수( t )가 있습니다.

 def ode_system(u, v, t): return [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]conditions = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, 조건, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution =solver.get_solution()

solution 호출 가능한 객체이므로 다음과 같이 numpy 배열이나 토치 텐서를 전달할 수 있습니다.

 u, v = 솔루션(t, to_numpy=True) # t는 np.ndarray 또는 torch.Tensor일 수 있습니다.

분석 솔루션에 대해 u 와 v 플로팅하면 다음과 같은 결과가 나옵니다.

PDE 시스템 예

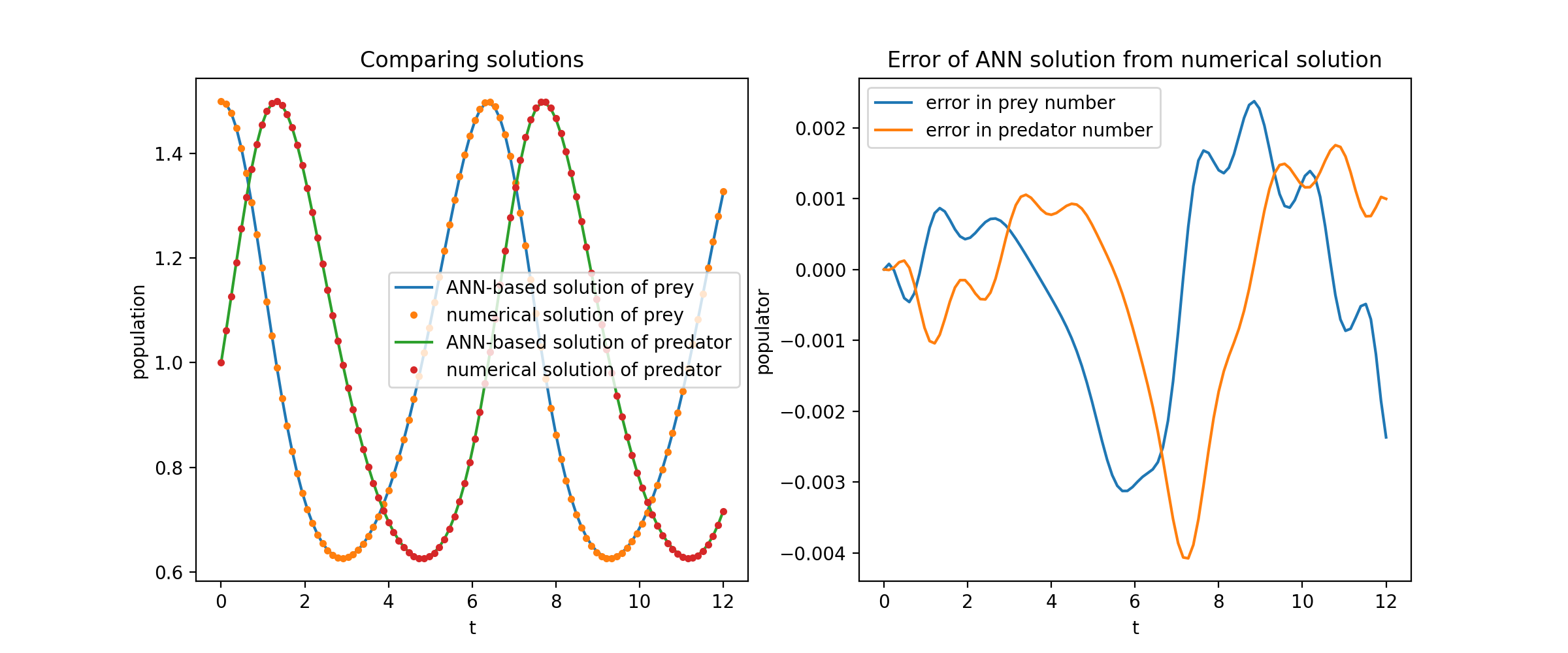
여기서는 직사각형의 Dirichlet 경계 조건을 사용하여 라플라스 방정식을 풉니다. 계산 분석 솔루션의 단순성을 위해 라플라스 방정식을 선택했습니다. 실제로 솔버를 충분히 잘 조정한다면 비선형, 카오스 PDE를 시도할 수 있습니다 .

2차원 PDE 시스템을 푸는 것은 경계값 문제에 대한 두 개의 변수 x 와 y 또는 초기 경계값 문제에 대한 x 와 t 모두 지원된다는 점을 제외하면 ODE를 푸는 것과 매우 유사합니다.

 def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: 토치. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=람다 x: 0, y_max=1, y_max_val=람다 x: 0,
                       )
]nets = [FCNN(n_input_units=2, n_output_units=1, Hidden_units=(512,))]solver = Solver2D(pde_system, 조건, xy_min=(0, 0), xy_max=(1, 1), nets=nets) solver.fit(max_epochs=2000)솔루션 =solver.get_solution()

2D PDE에 대한 solution 의 서명은 ODE의 솔루션 서명과 약간 다릅니다. 다시 말하지만, numpy 배열이나 토치 텐서를 사용합니다.

 u = 해(x, y, to_numpy=True)

[0,1] × [0,1] 에서 u를 평가하면 다음 플롯이 생성됩니다.

ANN 기반 솔루션	PDE의 잔차

모니터 사용

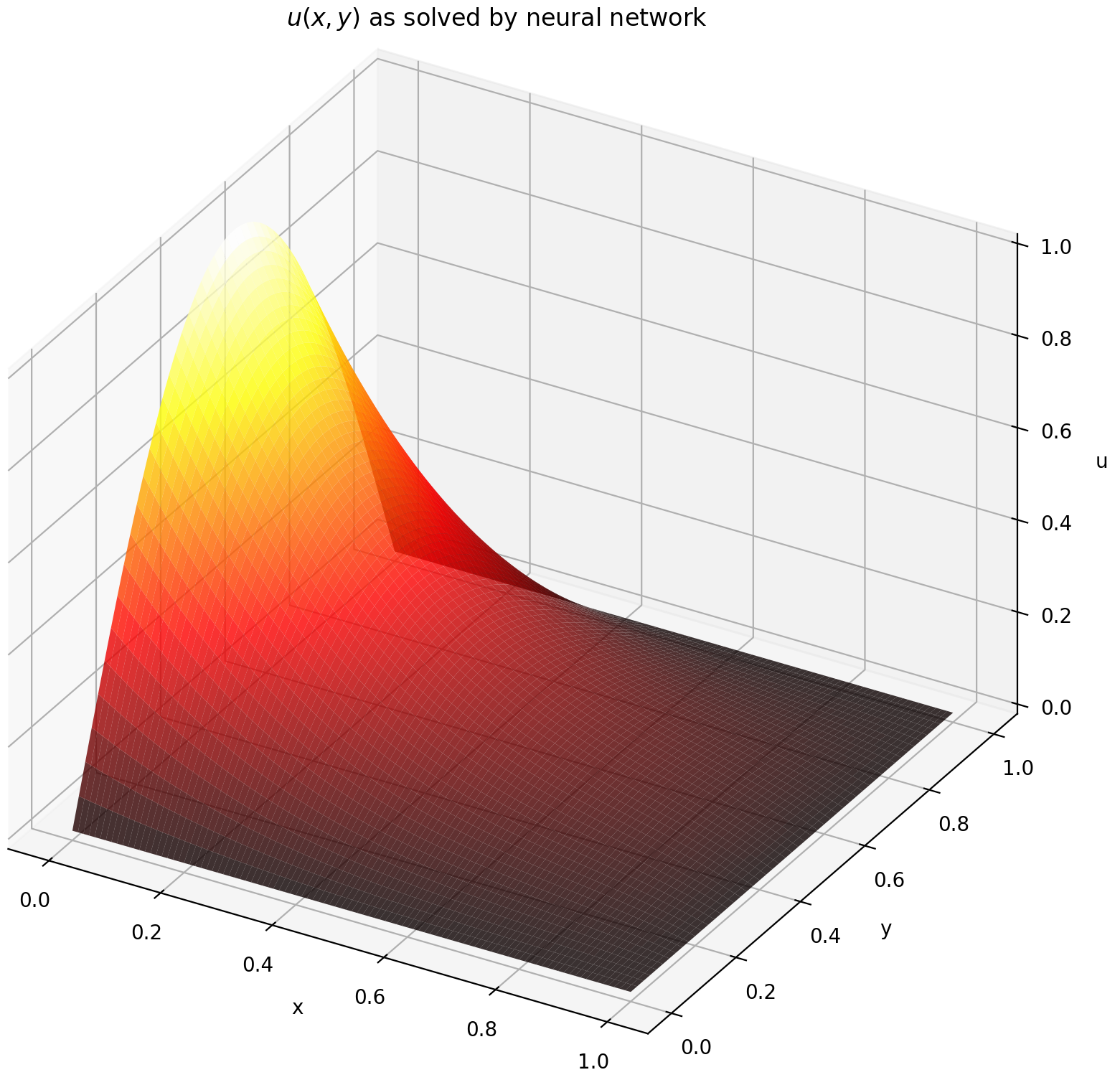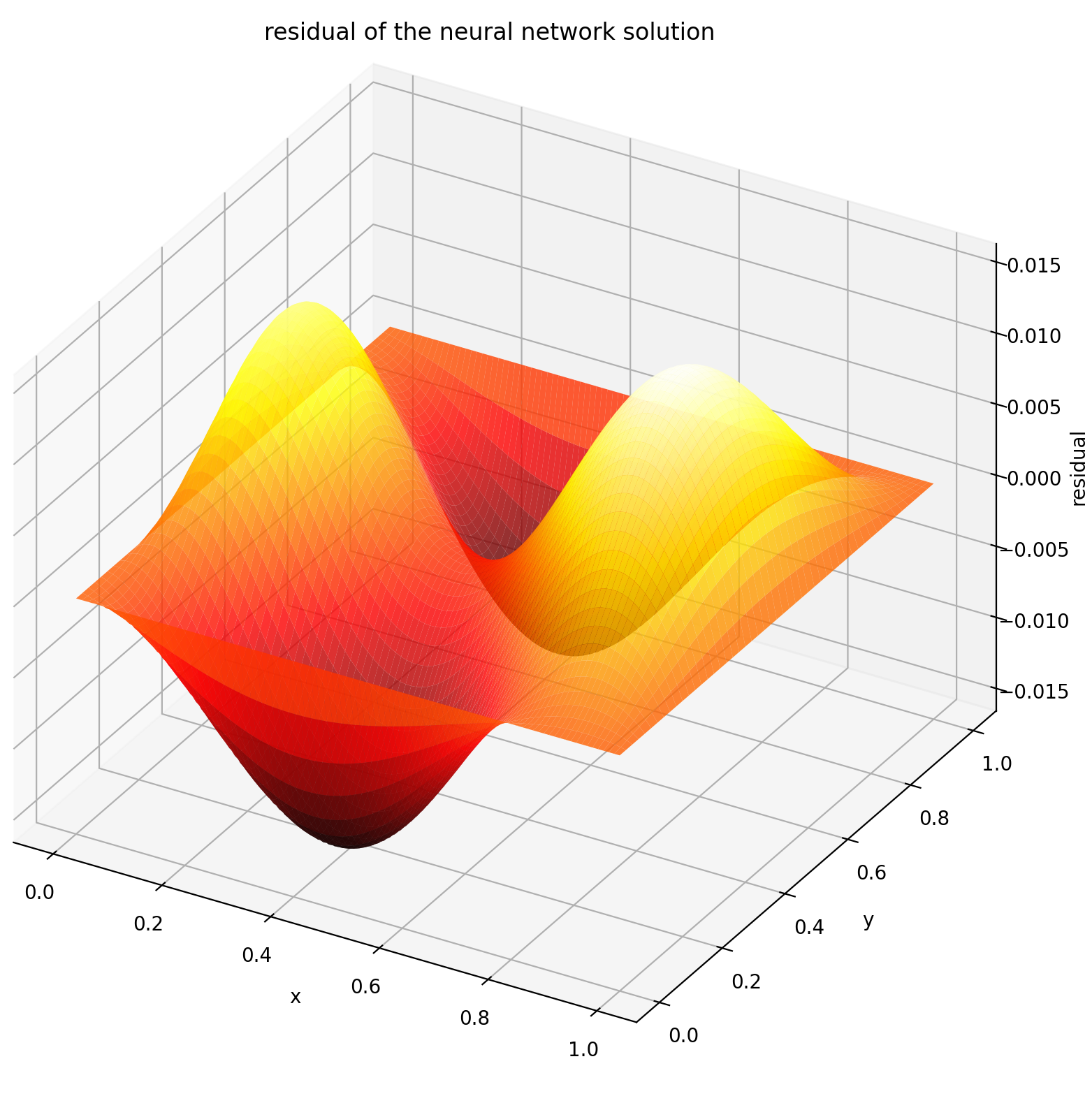모니터는 PDE/ODE 솔루션은 물론 훈련 중 손실 기록 및 사용자 정의 측정항목을 시각화하기 위한 도구입니다. Jupyter Notebooks 사용자는 %matplotlib notebook 매직을 실행해야 합니다. Jupyter Lab 사용자의 경우 %matplotlib widget 사용해 보세요.

 Neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])

플롯은 마지막 epoch 뿐만 아니라 100epoch마다 업데이트되어 두 개의 플롯을 표시합니다. 하나는 간격 [0,12] 의 솔루션 시각화용이고 다른 하나는 손실 기록(훈련 및 검증)용입니다.

맞춤형 네트워크

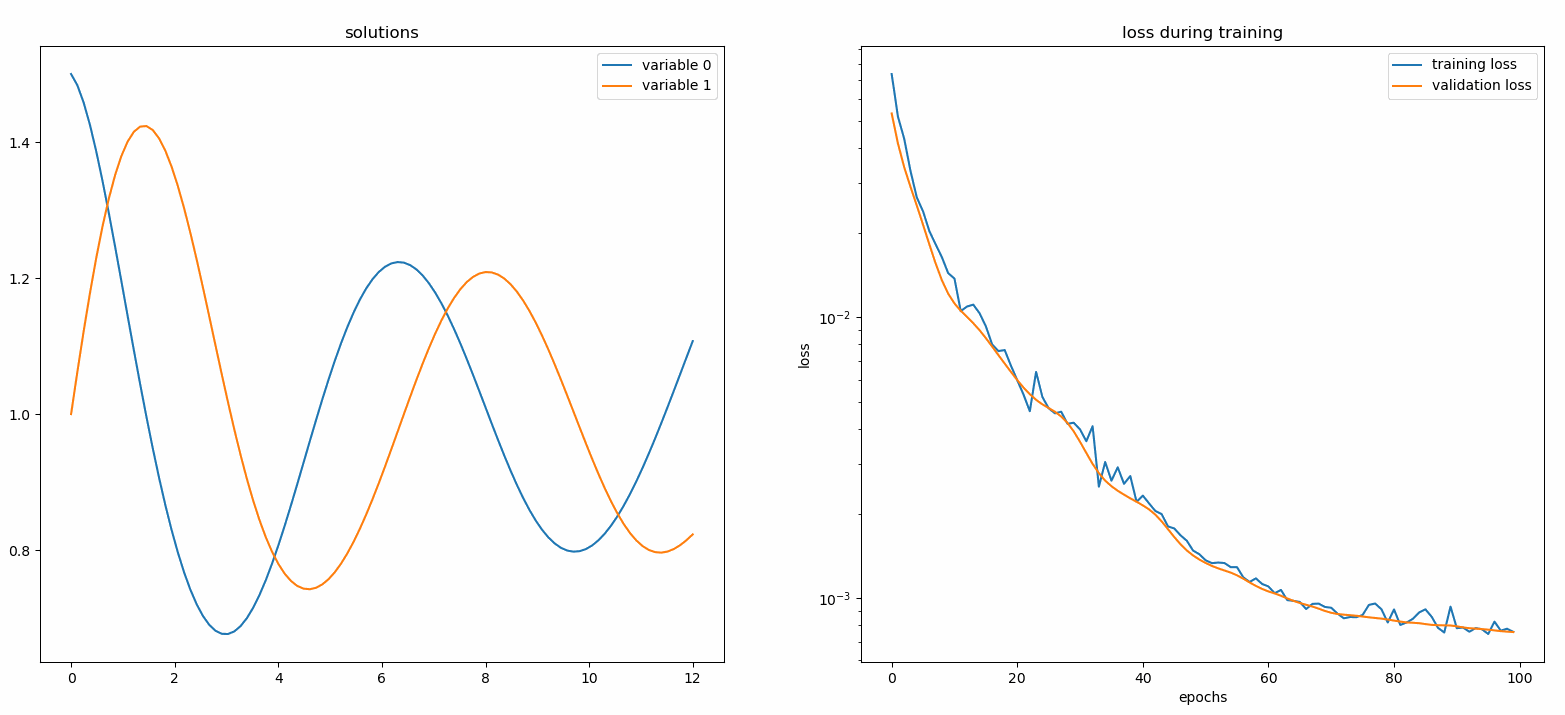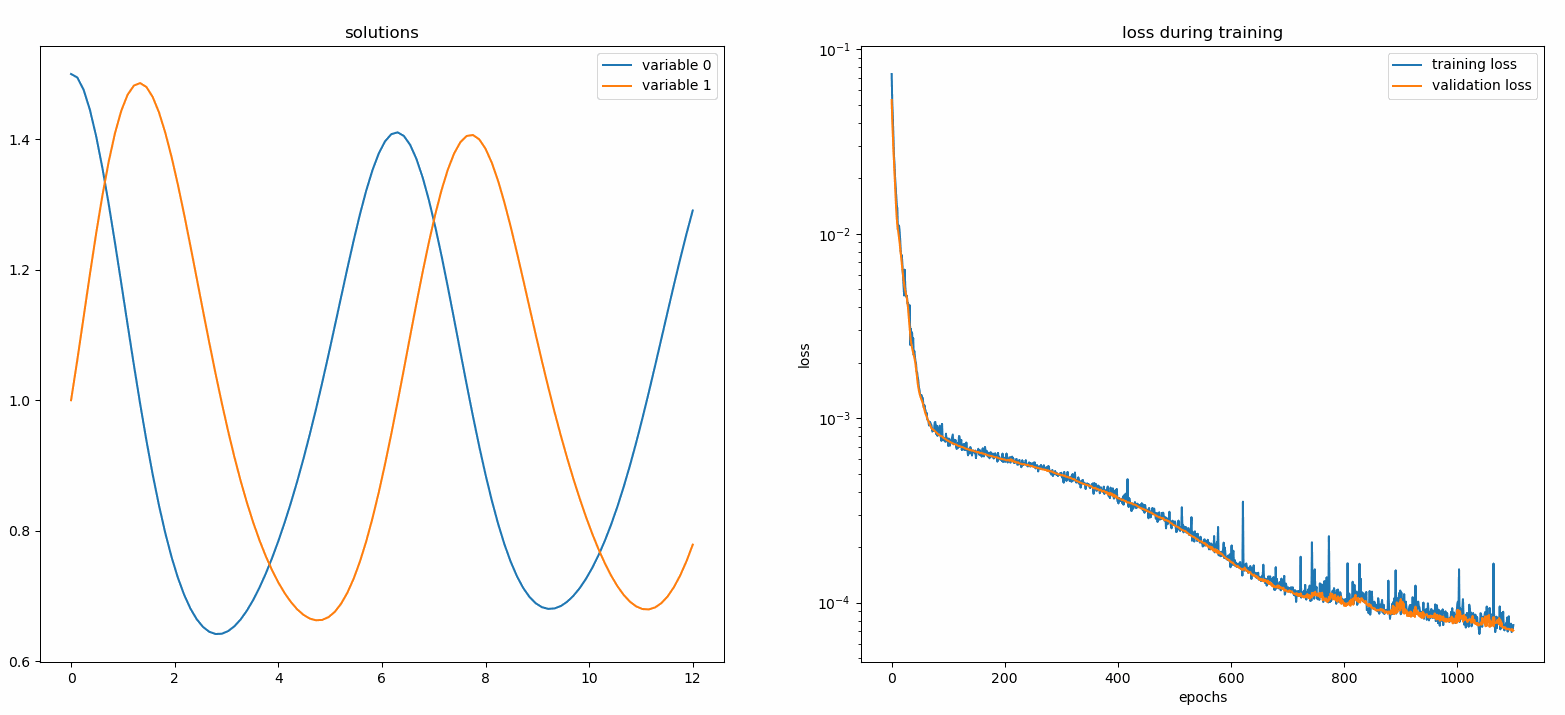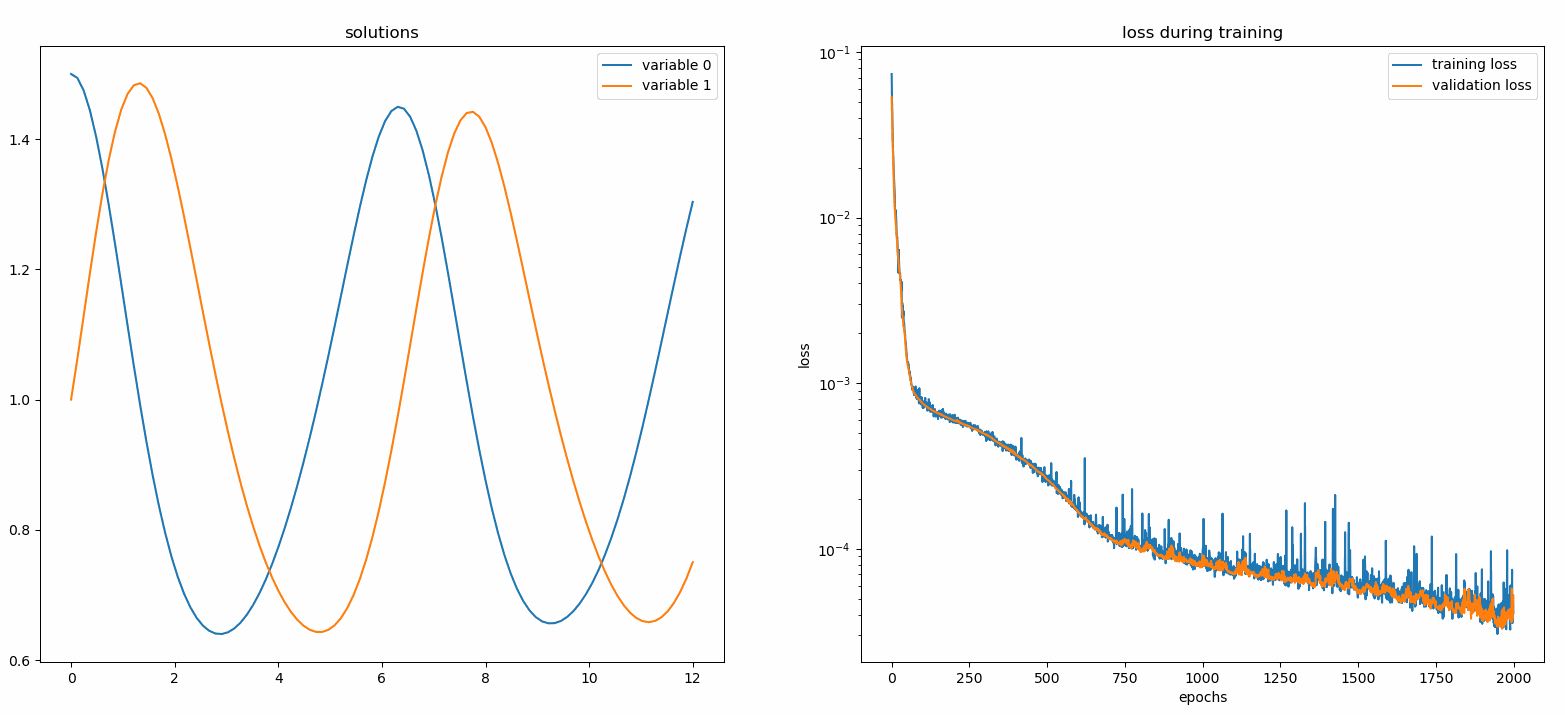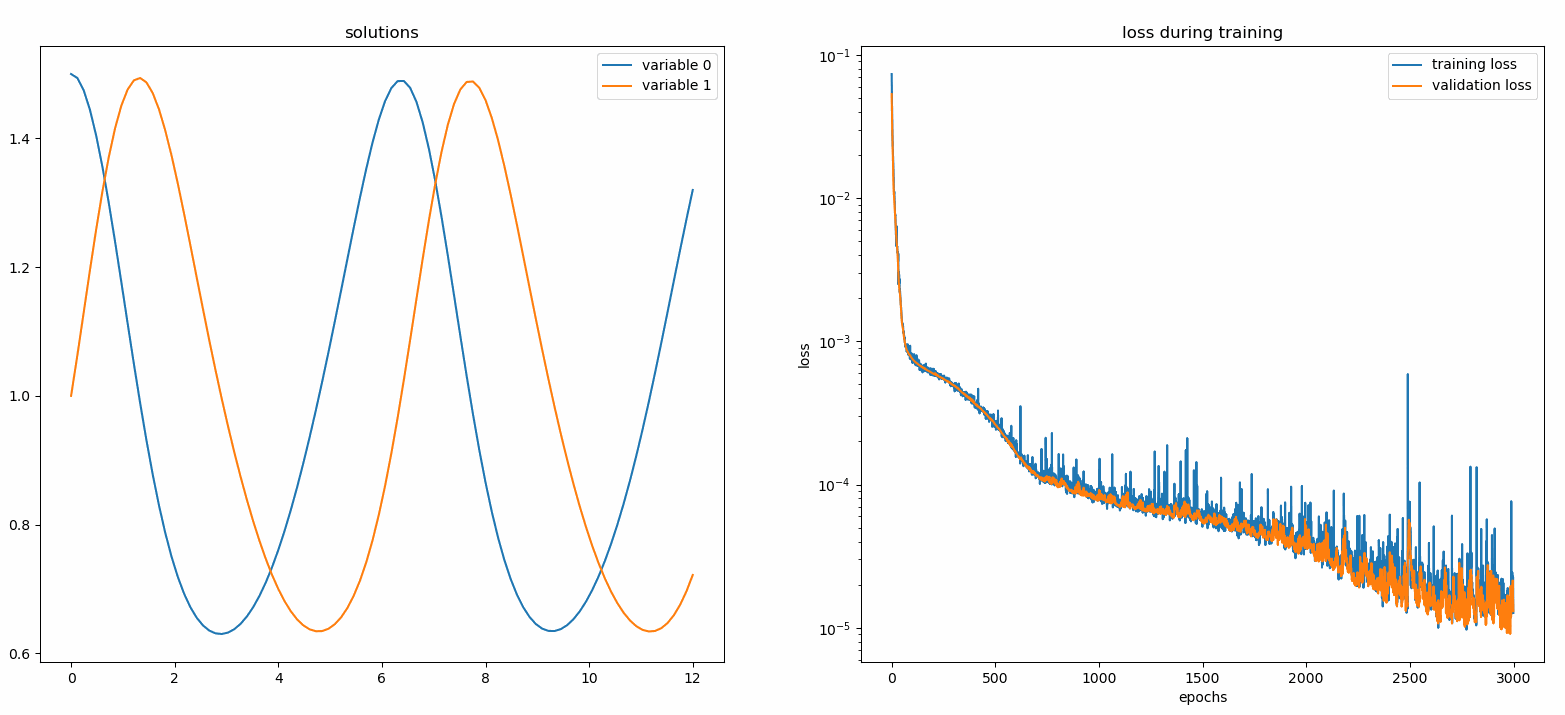
편의를 위해 우리는 숨겨진 유닛과 활성화 기능을 사용자 정의할 수 있는 완전 연결 신경망인 FCNN 구현했습니다.

 Neurodiffeq.networks import FCNN# 기본값: n_input_units=1, n_output_units=1, Hidden_units=[32, 32], 활성화=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., Hidden_units=[ ..., ..., ...], 활성화=...)
 ...nets = [net1, net2, ...]

FCNN 은 일반적으로 좋은 출발점입니다. 고급 사용자의 경우 솔버는 모든 사용자 정의 torch.nn.Module 과 호환됩니다. 유일한 제약은 다음과 같습니다:

1. 모듈은 (None, n_coords) 모양의 텐서를 취하고 (None, 1) 모양의 텐서를 출력합니다.

2. solver = Solver(..., nets=nets) 에 전달하려면 nets 에 총 n_funcs 모듈이 있어야 합니다.

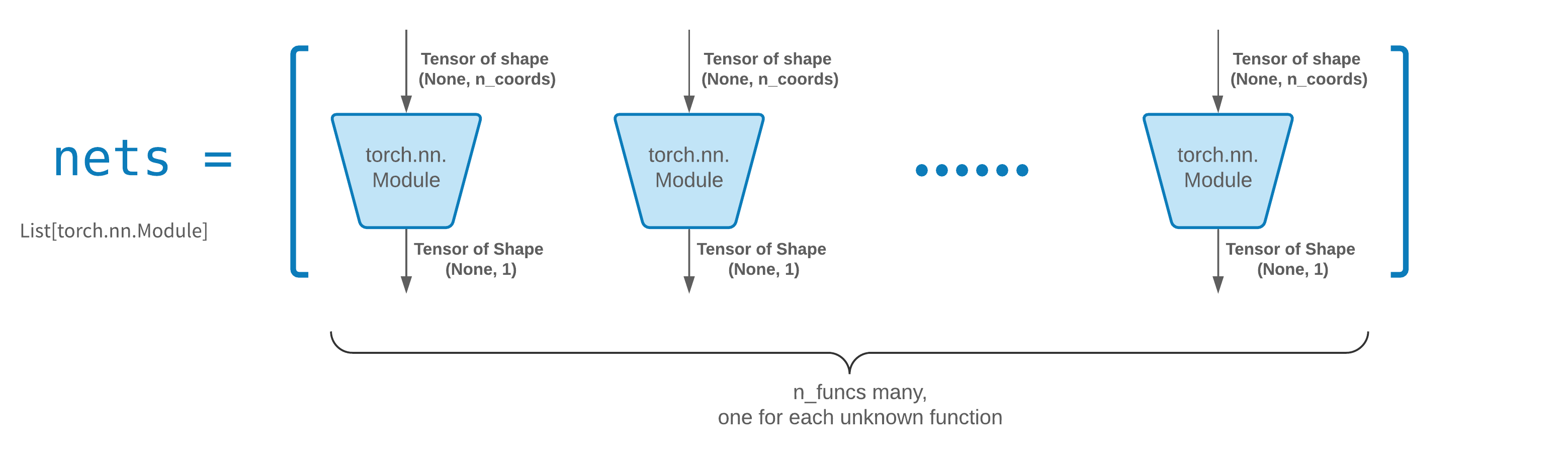
실제로, neurodiffeq 에는 위의 규칙을 따르지 않는 Single_net 기능이 있으므로 여기서는 다루지 않습니다.

자신만의 네트워크(모듈) 아키텍처 구축에 대한 PyTorch 튜토리얼을 읽어보세요.

전이 학습

전이 학습은 old_solver.nets (토치 모듈 목록)를 디스크에 직렬화한 다음 이를 로드하고 새 솔버에 전달하여 쉽게 수행됩니다.

 old_solver.fit(max_epochs=...)# ... `old_solver.nets`를 디스크에 덤프# ... 디스크에서 네트워크를 로드하고 `loaded_nets`에 저장합니다. Variablenew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)

현재 우리는 솔버의 네트워크 및 기타 내부 변수를 저장/로드하는 래퍼 함수를 ​​작업하고 있습니다. 그동안 네트워크 저장 및 로드에 대한 PyTorch 튜토리얼을 읽어보세요.

샘플링 전략

Neurodiffeq에서 네트워크는 도메인의 일련의 점에서 평가된 손실(ODE/PDE 잔차)을 최소화하여 훈련됩니다. 포인트는 매번 무작위로 리샘플링됩니다. 샘플링된 포인트의 수, 분포 및 경계 도메인을 제어하려면 자체 교육/검증 generator 를 지정할 수 있습니다.

 Neurodiffeq.generators import Generator1D# 기본값 t_min=0.0, t_max=1.0, method='uniform', Noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., Noise_std=...)g2 = Generator1D(크기=..., t_min=..., t_max=..., 방법=..., Noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)

다음은 Generator1D 의 일부 샘플 분포입니다.

Generator1D(8192, 0.0, 1.0, method='uniform')	Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3)

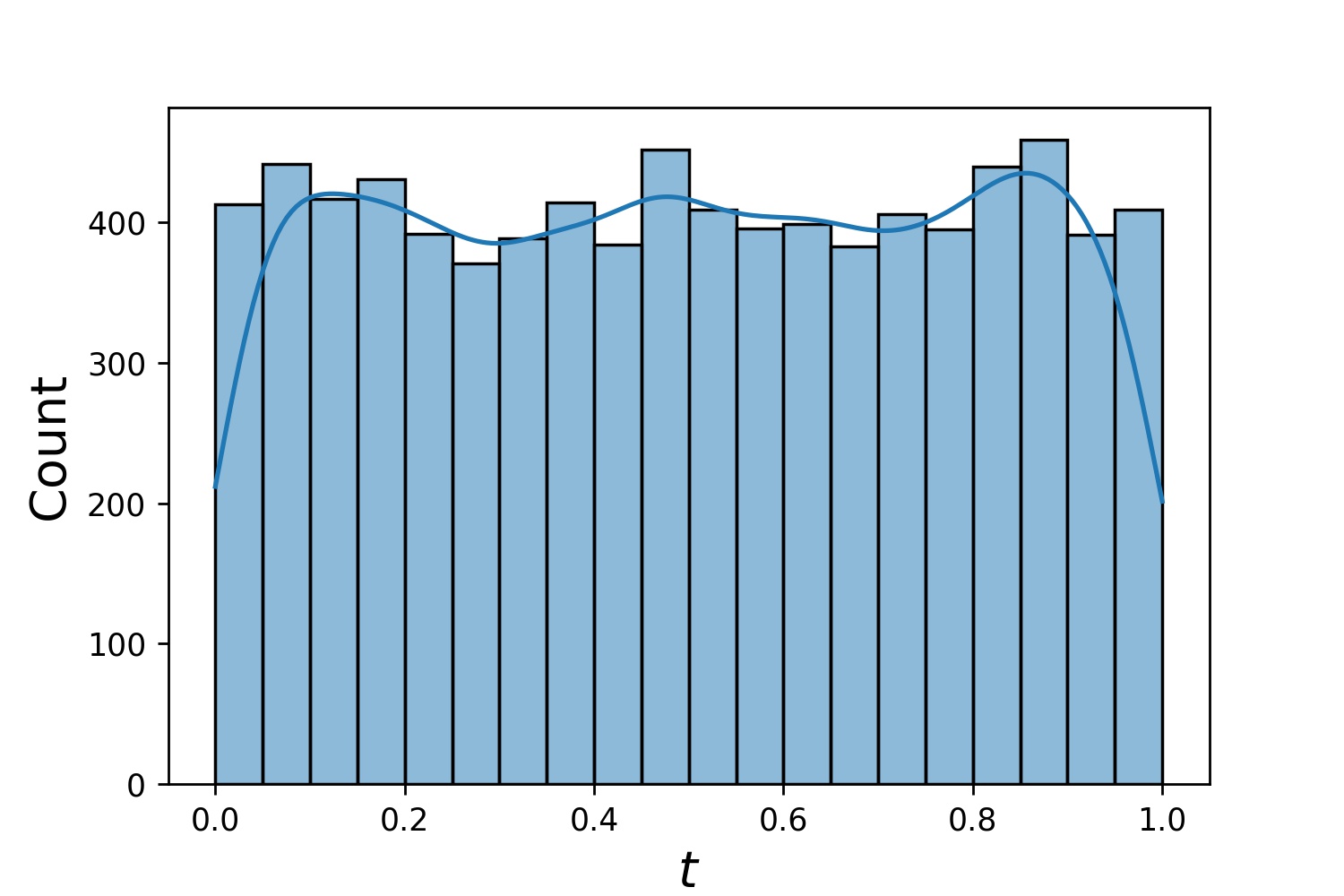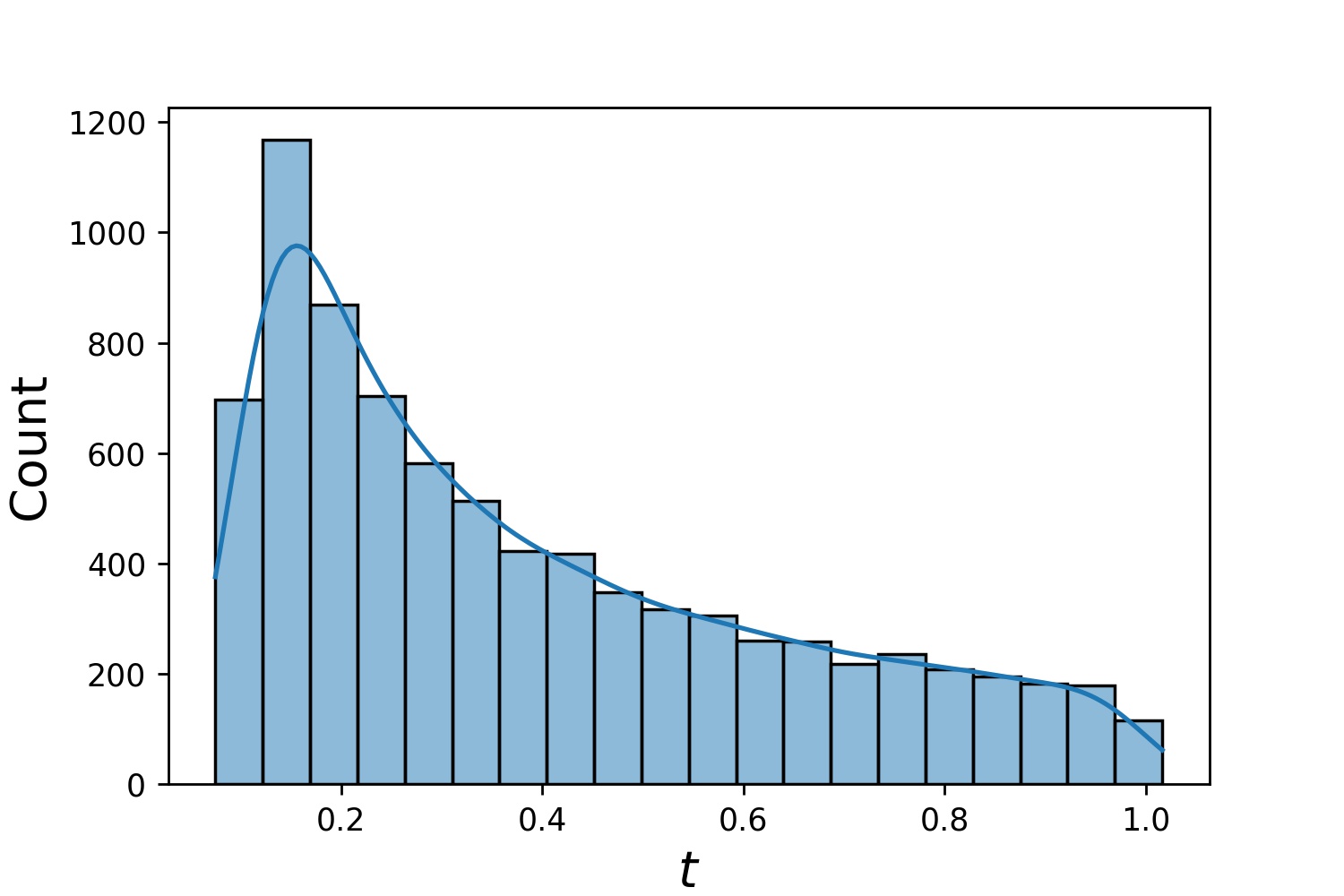train_generator 와 valid_generator 모두 지정하면 Solver1D(...) 에서 t_min 및 t_max 생략할 수 있습니다. 실제로 t_min , t_max , train_generator , valid_generator 함께 전달하더라도 t_min 및 t_max 여전히 무시됩니다.

생성기 결합

생성기의 또 다른 좋은 기능은 예를 들어 생성기를 연결할 수 있다는 것입니다.

 g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2

여기서 g g1 과 g2 의 결합된 샘플을 출력하는 생성기입니다.

g1	g2	g1 + g2

더 높은 차원 샘플링

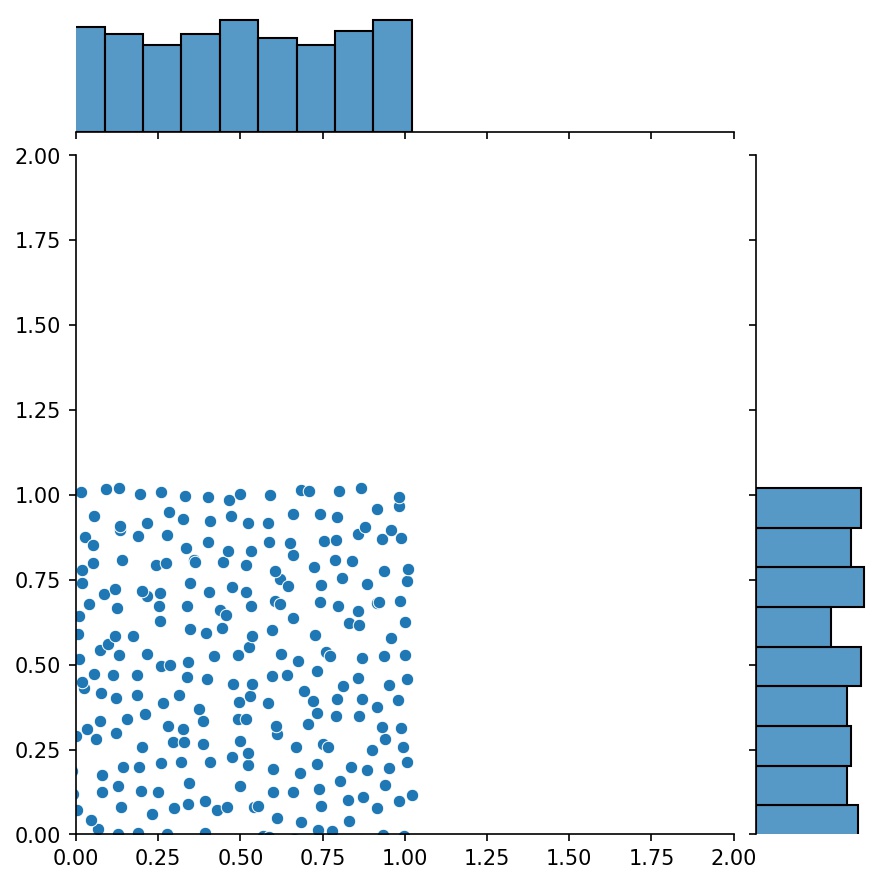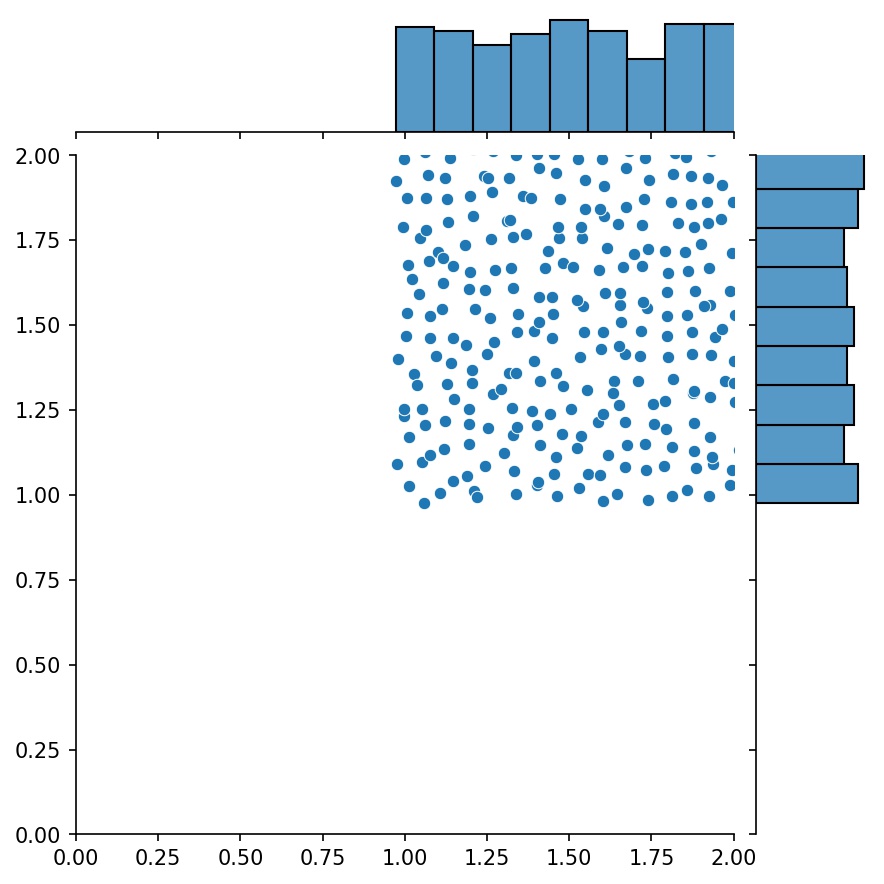더 높은 차원의 샘플링 포인트에는 Generator2D , Generator3D 등을 사용할 수 있습니다. 하지만 또 다른 방법도 있어요

 g1 = Generator1D(1024, 2.0, 3.0, 방법='균일')g2 = Generator1D(1024, 0.1, 1.0, 방법='log-spaced-noisy', Noise_std=0.001)g = g1 * g2

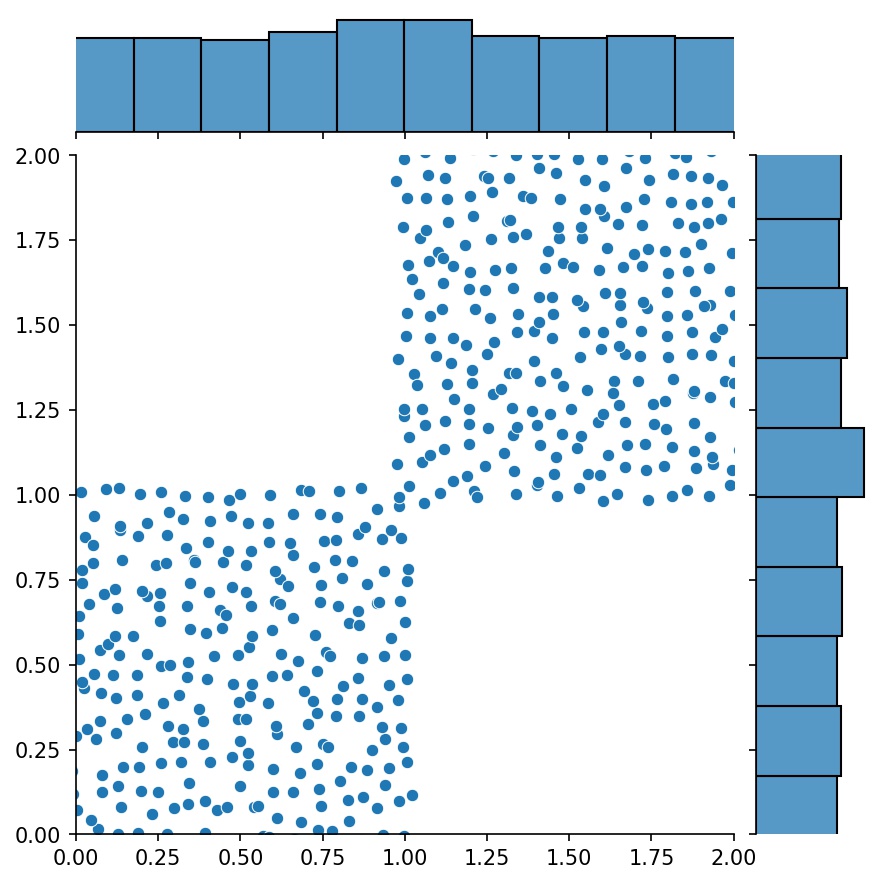
여기서 g 매번 2차원 직사각형 (2,3) × (0.1,1) 에 1024개의 포인트를 생성하는 생성기가 됩니다. 이들의 x 좌표는 uniform 전략을 사용하여 (2,3) 에서 추출되고 y 좌표는 log-spaced-noisy 전략을 사용하여 (0.1,1) 에서 추출됩니다.

g1	g2	g1 * g2

솔루션 번들 및 역 문제

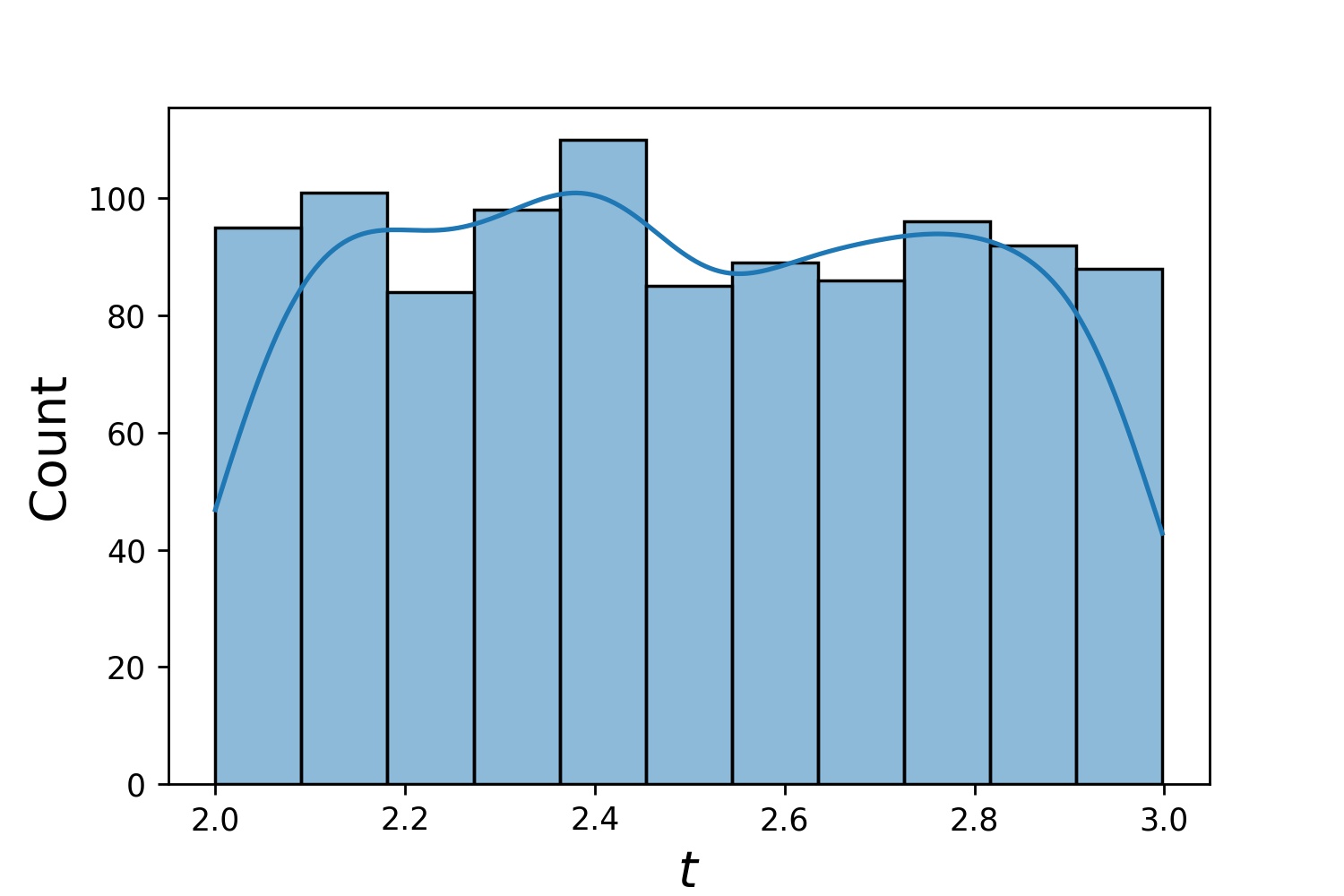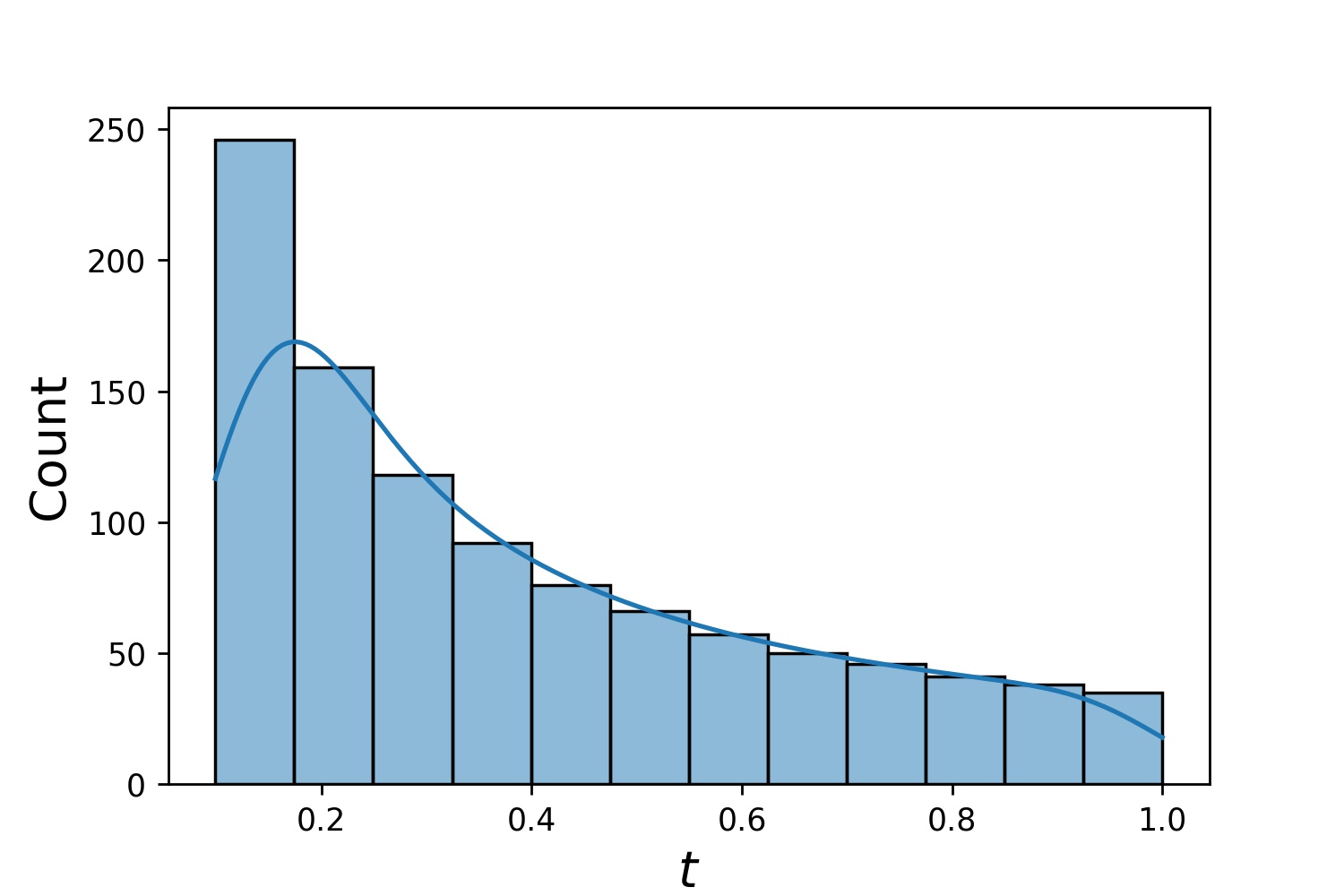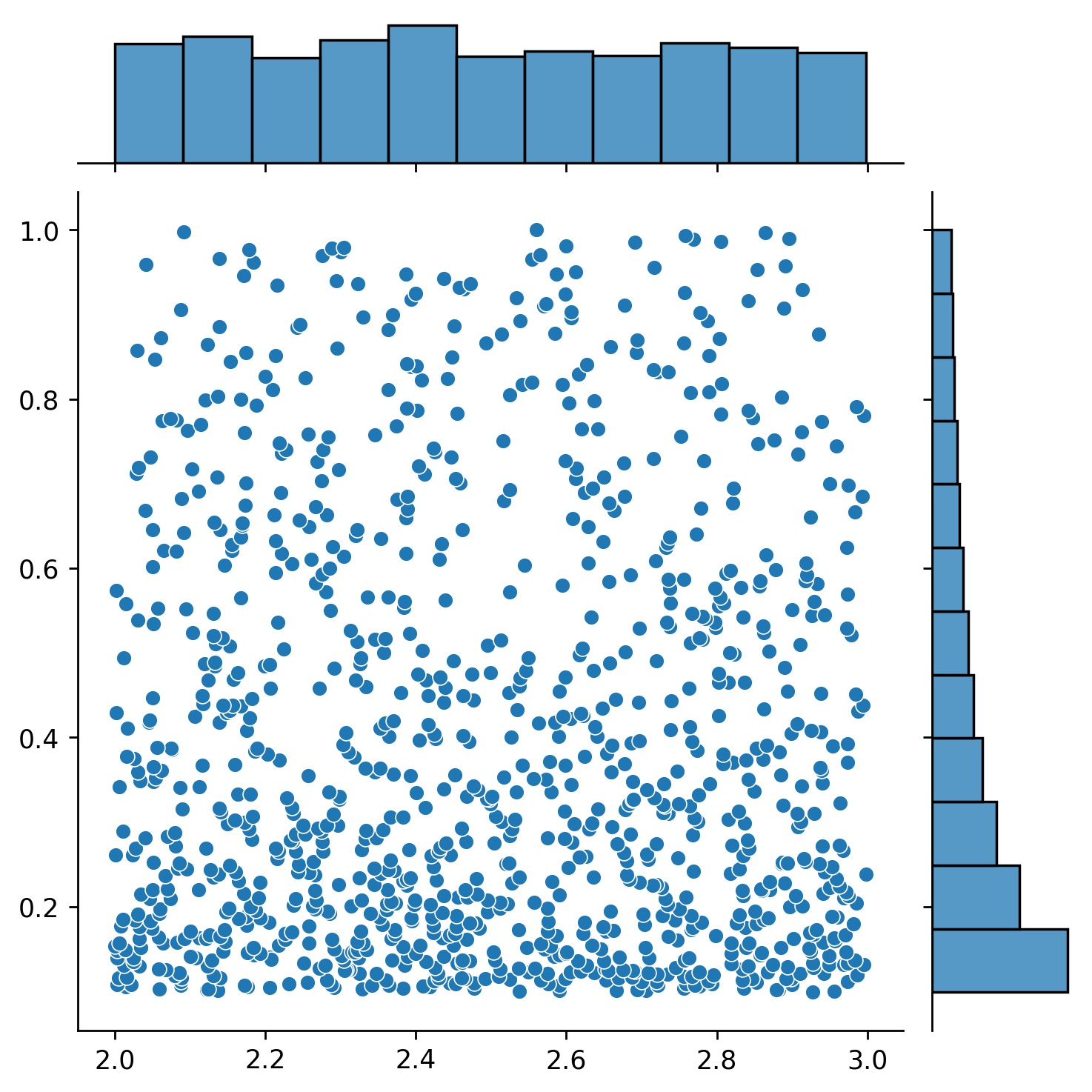때로는 방정식 묶음을 한 번에 푸는 것이 흥미로울 때도 있습니다. 예를 들어, 초기 조건 u(0) = U0 에서 du/dt + λu = 0 형식의 미분 방정식을 풀고 싶을 수 있습니다. 신경망에 대한 입력으로 처리하여 모든 λ 및 U0 에 대해 한 번에 이 문제를 해결하려고 할 수 있습니다.

이러한 응용 분야 중 하나는 반응 속도를 알 수 없는 화학 반응에 대한 것입니다. 다양한 반응 속도는 다양한 솔루션에 해당하며 단 하나의 솔루션만이 관찰된 데이터 포인트와 일치합니다. 먼저 솔루션 묶음을 해결한 다음 최상의 반응 속도(방정식 매개변수라고도 함)를 결정하는 데 관심이 있을 수 있습니다. 두 번째 단계는 역 문제 로 알려져 있습니다.

다음은 neurodiffeq 사용하여 이를 수행하는 방법에 대한 예입니다.

1. 방정식 du/dt + λu = 0 과 초기 조건 u(0) = U0 이 있다고 가정해 보겠습니다. 여기서 λ 와 U0 은 알 수 없는 상수입니다. 우리는 또한 일련의 관찰 t_obs 및 u_obs 가지고 있습니다. 먼저 솔루션 번들을 얻는 데 필요한 BundleSolver 및 BundleIVP 가져옵니다.

    Neurodiffeq.conditions import BundleIVPfrom Neurodiffeq.solvers import BundleSolver1Dimport matplotlib.pyplot as pltimport numpy as npimport torchfrom Neurodiffeq import diff

2. 입력 t 의 도메인과 매개변수 λ 및 U0 의 도메인을 결정합니다. 또한 매개변수의 순서를 결정해야 합니다. 즉, 어느 것이 첫 번째 매개변수이고 어느 것이 두 번째 매개변수여야 하는지입니다. 이 데모에서는 λ 첫 번째 매개변수(인덱스 0)로 선택하고 U0 두 번째 매개변수(인덱스 1)로 선택합니다. 매개변수의 인덱스를 추적하는 것이 매우 중요합니다.

    T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # 첫 번째 매개변수, 인덱스 = 0U0_MIN, U0_MAX = 0.2, 0.6 # 두 번째 매개변수, 인덱스 = 1

3. 그런 다음 IVP 및 Solver1D 대신 BundleIVP 및 BundleSolver1D 사용하는 것을 제외하고 평소와 같이 conditions 과 solver 정의합니다. 이 둘의 인터페이스는 IVP 및 Solver1D 와 매우 유사합니다. API 참조에서 자세한 내용을 확인할 수 있습니다.

    # 방정식 매개변수는 입력(보통 시간 및 공간 좌표) 뒤에 옵니다. diff_eq = 람다 u, t, lmd: [diff(u, t) + lmd * u]# BundleIVP에서 키워드 인수 이름은 "u_0"이어야 합니다. 다른 것을 사용하면(예: `y0`, `u0` 등) 작동하지 않습니다.conditions = [BundleIVP(t_0=0, u_0=None, Bundle_param_lookup={'u_0': 1}) # u_0에는 인덱스 1]solver = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ의 인덱스는 0이고, u_0의 인덱스는 1입니다.theta_max=[LAMBDA_MAX, U0_MAX], # λ의 인덱스는 0입니다. u_0의 인덱스는 1eq_param_index=(0,)입니다. 인덱스가 0n_batches_valid=1인 방정식 매개변수,
   )

   λ 는 방정식의 매개변수 이고 U0 초기 조건의 매개변수이므로 diff_eq 에 λ , 조건에 U0 포함해야 합니다. 매개변수가 방정식과 조건 모두에 존재하는 경우 두 위치 모두에 포함되어야 합니다. BundleSovler1D 에 전달된 conditions 의 모든 요소는 매개변수가 없더라도 Bundle* 조건이어야 합니다.

4. 이제 평소처럼 훈련하고 솔루션을 얻을 수 있습니다.

    solver.fit(max_epochs=1000)솔루션 =solver.get_solution(best=True)

   이 솔루션에는 t , λ 및 U0 의 세 가지 입력이 필요합니다. 모든 입력은 동일한 형태를 가져야 합니다. 예를 들어, λ=4 및 U0=0.4 고정하고 t ∈ [0,1] 에 대해 해 u 플로팅하는 데 관심이 있는 경우 다음을 수행할 수 있습니다.

    t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = 솔루션(t, lmd, u0, to_numpy=True) matplotlib.pyplot을 pltplt로 가져오기 .plot(티, 유)

5. 번들 solution 있으면 관찰된 데이터 포인트 (t_i, u_i) 와 가장 밀접하게 일치하는 매개변수 세트 (λ, U0) 를 찾을 수 있습니다. 이는 간단한 경사하강법을 사용하여 달성됩니다. 다음 장난감 예에서는 u(0.2) = 0.273 , u(0.5)=0.129 및 u(0.8) = 0.0609 세 개의 데이터 포인트만 있다고 가정합니다. 다음은 고전적인 PyTorch 작업 흐름입니다.

    # 관찰된 데이터 포인트t_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# 무작위 초기화 λ와 U0; 그래디언트를 추적하세요lmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(참)], lr=1e-2)# _ in range(10000)에 대해 10000 epoch 동안 경사하강법을 실행합니다:output = Solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs))loss = ((output - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
      print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, 손실 = {loss.item()}")

FAQ

Q: 훈련에 GPU를 사용하는 방법은 무엇입니까?

단순한. Neurodiffeq를 가져올 때 라이브러리는 컴퓨터에서 CUDA를 사용할 수 있는지 자동으로 감지합니다. 라이브러리는 PyTorch를 기반으로 하기 때문에 호환되는 GPU 장치가 발견되면 기본 텐서 유형을 torch.cuda.DoubleTensor 로 설정합니다.

Q: 사전 훈련된 네트를 사용하는 방법은 무엇입니까?

사용자 정의 네트워크 및 전이 학습 섹션을 참조하세요.

Q: 학습률을 변경하는 방법은 무엇입니까?

표준 PyTorch 방식입니다.

1. 사용자 정의 네트워크: nets = [FCNN(), FCN(), ...] 에 설명된 대로 네트워크를 구축하십시오.

2. 사용자 정의 최적화 프로그램을 인스턴스화하고 이러한 네트워크의 모든 매개변수를 전달합니다.

    parameters = [p for net in nets for p in net.parameters()] # 모든 네트워크의 매개변수 목록MY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)

3. nets 와 optimizer 모두 솔버에 전달합니다: solver = Solver1D(..., nets=nets, optimizer=optimizer)

Q: 잘못된 해결책을 얻었습니다.

기존 수치법(FEM, FVM 등)과 달리 NN 기반 솔루션에는 약간의 하이퍼튜닝이 필요합니다. 라이브러리는 하이퍼파라미터의 모든 조합을 시도할 수 있는 최고의 유연성을 제공합니다.

• 다른 네트워크 아키텍처를 사용하려면 사용자 정의 torch.nn.Module 을 전달할 수 있습니다.

• 다른 옵티마이저를 사용하려면 자체 옵티마이저를 solver = Solver(..., optimizer=my_optim) 에 전달할 수 있습니다.

• 다른 샘플링 분포를 사용하려면 내장 생성기를 사용하거나 처음부터 자체 생성기를 작성할 수 있습니다.

• 다른 샘플링 크기를 사용하려면 생성기를 조정하거나 solver = Solver(..., n_batches_train) 변경할 수 있습니다.

• 훈련 중에 하이퍼파라미터를 동적으로 변경하려면 콜백 기능을 확인하세요.

Q: 경험에 따른 규칙이 있나요?

• ReLU 활성화에 사용하지 마세요. 2차 도함수는 동일하게 0이기 때문입니다.

• PDE/ODE를 무차원 형식으로 다시 조정하고 모든 범위를 [0,1] 로 만드는 것이 좋습니다. [0,1000000] 과 같은 도메인으로 작업하는 것은 a) PyTorch가 모듈 가중치를 상대적으로 작게 초기화하고 b) 대부분의 활성화 함수(예: Sigmoid, Tanh, Swish)가 0에 가까운 비선형이기 때문에 실패하기 쉽습니다.

• PDE/ODE가 너무 복잡하다면 커리큘럼 학습을 시도해 보세요. 더 작은 도메인에서 네트워크 교육을 시작한 다음 전체 도메인이 포함될 때까지 점차적으로 확장하십시오.

기여

누구나 이 프로젝트에 기여할 수 있습니다.

이 저장소에 기여할 때 우리는 다음 프로세스를 고려합니다.

1. 이슈를 열어 계획 중인 변경 사항에 대해 논의하세요.

2. 기여 지침을 살펴보세요.

3. 포크된 저장소를 변경하고 인터페이스가 변경되면 README.md를 업데이트하세요.

4. 풀 요청을 엽니다.