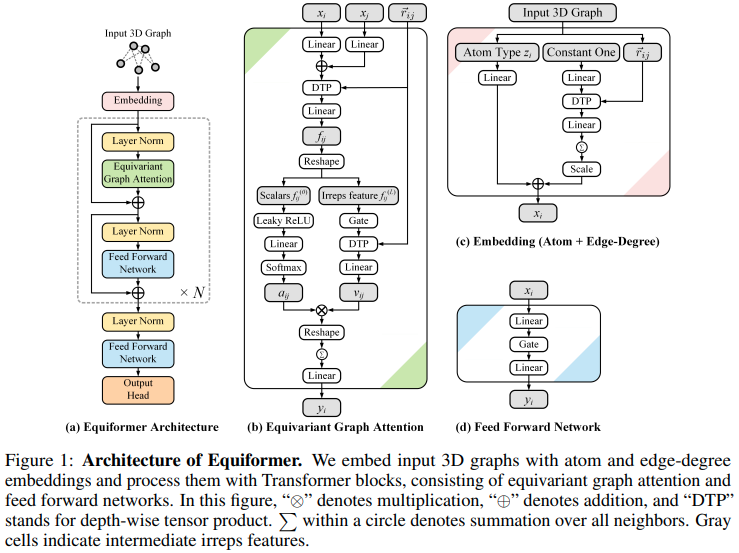
equiformer pytorch 다운로드 - equiformer pytorch 소스 코드 다운로드

Equiformer - Pytorch (wip)

새로운 SOTA에 도달하고 단백질 접힘을 위해 EquiFold(Prescient Design)에서 사용하도록 채택된 SE3/E3 등변적 주의 네트워크인 Equiformer의 구현

이 디자인은 SE3 Transformers를 기반으로 구축된 것으로 보이며 내적 주의가 MLP 주의로 대체되고 GATv2에서 전달되는 비선형 메시지가 사용됩니다. 또한 좀 더 효율성을 높이기 위해 깊이별 텐서 곱을 수행합니다. 제가 착각하고 있다고 생각하시면 언제든지 이메일을 보내주세요.

업데이트: SE3 등변 네트워크의 각도 확장을 획기적으로 향상시키는 새로운 개발이 이루어졌습니다! 이 문서에서는 먼저 z축(또는 다른 관례에 따라 y축)을 따라 표현을 정렬하면 구형 고조파가 희박해진다는 점에 주목했습니다. 그러면 방정식에서 m _f 차원이 제거됩니다. Passaro et al.의 후속 논문. Clebsch Gordan 행렬도 희소화되어 _mi 및 l _f 가 제거된다는 점에 주목했습니다. 또한 담당자를 한 축으로 정렬한 후 문제가 SO(3)에서 SO(2)로 감소했다는 연결도 만들었습니다. Equiformer v2(공식 저장소)는 변환기와 같은 프레임워크에서 이를 활용하여 새로운 SOTA에 도달합니다.

이에 대해 확실히 더 많은 작업/탐색을 투입할 것입니다. 지금은 SO(2)로의 완전한 변환을 위해 제외하고 Equiformer v1에 대한 처음 두 논문의 트릭을 통합했습니다.

업데이트 2: 더 높은 수준의 담당자 간에 상호 작용이 없는 새로운 SOTA가 있는 것으로 보입니다(즉, 모든 텐서 제품/clebsch gordan 수학이 사라짐). HEGNN을 변형한 것으로 보이는 GotenNet

설치하다

$ pip install equiformer-pytorch

용법

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),               # dimensions per type, ascending, length must match number of degrees (num_degrees)
    dim_head = ( 4 , 4 , 4 ),          # dimension per attention head
    heads = ( 2 , 2 , 2 ),             # number of attention heads
    num_linear_attn_heads = 0 ,     # number of global linear attention heads, can see all the neighbors
    num_degrees = 3 ,               # number of degrees
    depth = 4 ,                     # depth of equivariant transformer
    attend_self = True ,            # attending to self or not
    reduce_dim_out = True ,         # whether to reduce out to dimension of 1, say for predicting new coordinates for type 1 features
    l2_dist_attention = False      # set to False to try out MLP attention
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask ) # (1, 128)

out . type0 # invariant type 0    - (1, 128)
out . type1 # equivariant type 1  - (1, 128, 3)

이 저장소에는 가역적 네트워크를 사용하여 깊이에서 메모리 사용량을 분리하는 방법도 포함되어 있습니다. 즉, 깊이를 늘리면 하나의 등형 변환기 블록(어텐션 및 피드포워드)을 사용할 때 메모리 비용이 일정하게 유지됩니다.

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),
    dim_head = ( 4 , 4 , 4 ),
    heads = ( 2 , 2 , 2 ),
    num_degrees = 3 ,
    depth = 48 ,          # depth of 48 - just to show that it runs - in reality, seems to be quite unstable at higher depths, so architecture stil needs more work
    reversible = True ,   # just set this to True to use https://arxiv.org/abs/1707.04585
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask )

out . type0 . sum (). backward ()

가장자리

가장자리 있음, 예: 원자 결합

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

out = model ( atoms , coors , mask , edges = bonds )

out . type0 # (2, 32)
out . type1 # (2, 32, 3)

인접 행렬 포함

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    reduce_dim_out = True ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    num_adj_degrees_embed = 2 ,       # this will derive the second degree connections and embed it correctly
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat )

out . type0 # (1, 128)
out . type1 # (1, 128, 3)

감사

넉넉한 후원을 위한 StabilityAI와 저의 다른 후원자들

테스트

등분산 검정 등

$ python setup.py test

예

먼저 sidechainnet 설치하세요

$ pip install sidechainnet

그런 다음 단백질 백본 노이즈 제거 작업을 실행합니다.

$ python denoise.py

토도

인용

 @article { Liao2022EquiformerEG ,
    title   = { Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs } ,
    author  = { Yi Liao and Tess E. Smidt } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.11990 }
}

 @article { Lee2022.10.07.511322 ,
    author  = { Lee, Jae Hyeon and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and Cho, Kyunghyun and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard } ,
    title   = { EquiFold: Protein Structure Prediction with a Novel Coarse-Grained Structure Representation } ,
    elocation-id = { 2022.10.07.511322 } ,
    year    = { 2022 } ,
    doi     = { 10.1101/2022.10.07.511322 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322 } ,
    eprint  = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Shazeer2019FastTD ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam M. Shazeer } ,
    journal = { ArXiv } ,
    year    = { 2019 } ,
    volume  = { abs/1911.02150 }
}

 @misc { ding2021cogview ,
    title   = { CogView: Mastering Text-to-Image Generation via Transformers } ,
    author  = { Ming Ding and Zhuoyi Yang and Wenyi Hong and Wendi Zheng and Chang Zhou and Da Yin and Junyang Lin and Xu Zou and Zhou Shao and Hongxia Yang and Jie Tang } ,
    year    = { 2021 } ,
    eprint  = { 2105.13290 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @inproceedings { Kim2020TheLC ,
    title   = { The Lipschitz Constant of Self-Attention } ,
    author  = { Hyunjik Kim and George Papamakarios and Andriy Mnih } ,
    booktitle = { International Conference on Machine Learning } ,
    year    = { 2020 }
}

 @article { Zitnick2022SphericalCF ,
    title   = { Spherical Channels for Modeling Atomic Interactions } ,
    author  = { C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.14331 }
}

 @article { Passaro2023ReducingSC ,
  title     = { Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs } ,
  author    = { Saro Passaro and C. Lawrence Zitnick } ,
  journal   = { ArXiv } ,
  year      = { 2023 } ,
  volume    = { abs/2302.03655 }
}

 @inproceedings { Gomez2017TheRR ,
    title   = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author  = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse } ,
    booktitle = { NIPS } ,
    year    = { 2017 }
}

 @article { Bondarenko2023QuantizableTR ,
    title   = { Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing } ,
    author  = { Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort } ,
    journal = { ArXiv } ,
    year    = { 2023 } ,
    volume  = { abs/2306.12929 } ,
    url     = { https://api.semanticscholar.org/CorpusID:259224568 }
}

 @inproceedings { Arora2023ZoologyMA ,
  title   = { Zoology: Measuring and Improving Recall in Efficient Language Models } ,
  author  = { Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e } ,
  year    = { 2023 } ,
  url     = { https://api.semanticscholar.org/CorpusID:266149332 }
}