Tic-Tac-Toe(또는 Noughts and Crosses) 게임에 Minimax AI 알고리즘을 구현합니다. 시도해 보세요: Tic-tac-toe - Minimax
AI를 활용한 게임 해결을 위해 게임 트리의 개념과 미니맥스 알고리즘을 소개하겠습니다. 게임의 다양한 상태는 게임 트리의 노드로 표시되며, 이는 위의 계획 문제와 매우 유사합니다. 생각이 조금 다를 뿐입니다. 게임 트리에서 노드는 게임에서 각 플레이어의 차례에 해당하는 레벨로 배열되어 트리의 "루트" 노드(보통 다이어그램 상단에 표시됨)가 게임의 시작 위치가 됩니다. tic-tac-toe에서는 아직 X나 Os가 재생되지 않은 빈 그리드가 됩니다. 루트 아래의 두 번째 수준에는 첫 번째 플레이어의 움직임으로 인해 발생할 수 있는 X 또는 O의 상태가 있습니다. 우리는 이러한 노드를 루트 노드의 "자식"이라고 부릅니다.
두 번째 수준의 각 노드는 상대 플레이어의 이동으로 도달할 수 있는 상태를 하위 노드로 갖습니다. 이는 게임이 끝나는 상태에 도달할 때까지 레벨별로 계속됩니다. tic-tac-toe에서는 플레이어 중 한 명이 3라인을 얻어 승리하거나, 보드가 가득 차서 게임이 무승부로 끝나는 것을 의미합니다.
미니맥스(Minimax)는 틱택토, 체커, 체스, 바둑 등 2인용 게임에 적용되는 인공지능이다. 이 게임은 수학적 표현에서 한 플레이어가 승리하고(+1) 다른 플레이어가 패배(-1)하거나 두 플레이어 모두 승리하지 못하기 때문에(0) 제로섬 게임으로 알려져 있습니다.
알고리즘은 Max 플레이어가 승리하거나 패하지 않도록(무승부) 유도하는 최선의 움직임을 반복적으로 검색합니다. 게임의 현재 상태와 해당 상태에서 사용 가능한 이동을 고려한 다음 최종 상태(승리, 무승부 또는 패배)를 찾을 때까지 각 유효한 이동에 대해 재생합니다( min 및 max 번갈아 가며).
이 알고리즘은 Algorithms in a Nutshell(George Heineman, Gary Pollice, Stanley Selkow, 2009)이라는 책에서 연구되었습니다. 유사 코드(개정):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
이제 Python 구현을 통해 이 의사코드의 각 부분을 살펴보겠습니다. Python 구현은 이 저장소에서 사용할 수 있습니다. 우선 다음을 고려하십시오.
보드 = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
최대 = +1
최소 = -1
MAX는 X 또는 O일 수 있고 MIN은 O 또는 X일 수 있습니다. 보드는 3x3입니다.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]두 플레이어 모두 최악의 점수로 시작합니다. 플레이어가 MAX인 경우 점수는 -무한대입니다. 그렇지 않으면 플레이어가 MIN이면 점수는 +무한대입니다. 참고: 무한대 는 inf의 별칭입니다(Python의 math 모듈에서).
보드에서 가장 좋은 수는 모두 [-1, -1](행과 열)입니다.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return score깊이가 0이면 보드에 재생할 새 빈 셀이 없는 것입니다. 또는 플레이어가 이기면 게임은 MAX 또는 MIN 동안 종료됩니다. 따라서 해당 상태의 점수가 반환됩니다.
이제 재귀를 포함하는 이 코드의 주요 부분을 살펴보겠습니다.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y각 유효한 이동에 대해(빈 셀):
보드의 이동(+1 또는 -1)이 실행 취소되고 행, 열이 수집됩니다.
다음 단계는 점수를 최고 점수와 비교하는 것입니다.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreMAX 플레이어의 경우 더 높은 점수를 받게 됩니다. MIN 플레이어의 경우 더 낮은 점수를 받게 됩니다. 그리고 결국, 최선의 수는 반환됩니다. 최종 알고리즘:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best 아래에서는 최대값이 왼쪽의 두 번째 노드에 있으므로 가장 좋은 이동은 가운데에 있습니다.
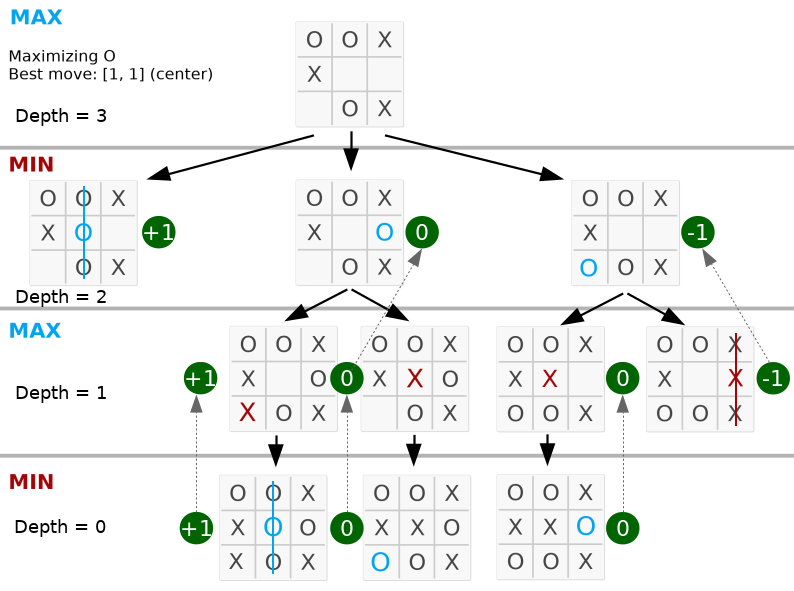
깊이가 보드의 유효한 움직임과 동일한지 살펴보세요. 전체 코드는 py_version/ 에서 확인할 수 있습니다.
단순화된 게임 트리:
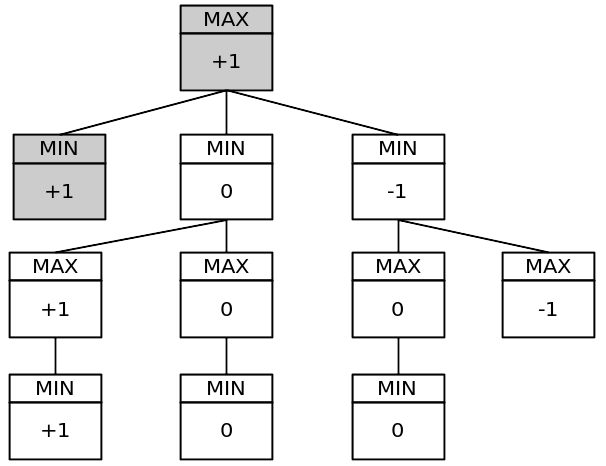
해당 트리에는 11개의 노드가 있습니다. 전체 게임 트리에는 549.946개의 노드가 있습니다! 프로그램에 정적 전역 변수를 넣고 차례대로 각 minimax 함수 호출에 대해 이를 증가시켜 테스트할 수 있습니다.
체스와 같은 보다 복잡한 게임에서는 전체 게임 트리를 검색하기가 어렵습니다. 그러나 Alpha-beta Pruning은 검색에서 관련 없는 노드(하위 트리)를 잘라내기 때문에 검색 트리의 일부 분기를 무시할 수 있게 해주는 minimax 알고리즘의 최적화 방법입니다. 자세한 내용은 다음을 참조하세요.