매우 큰 큐브를위한 Rubik 's Cube Solver.
크기의 모든 큐브를 1에서 65536까지 해결합니다. 더 큰 큐브를 처리하도록 코드를 쉽게 수정할 수 있습니다. 그러나 기본 제한은 시스템의 메모리 양과 해결하는 데 걸리는 시간입니다. 시간 해결 시간은 ~ n^2가 자랍니다. 즉, 각 차원에서 2 배 더 큰 큐브를 해결하는 데 4-5 배 더 오래 걸립니다.
1024 층 큐브는 약 1.5 초 안에 해결할 수 있습니다. 16384 층 큐브는 약 20 분 안에 해결 될 수 있습니다.
YouTube : 65536 레이어 해결 YouTube : 32768 레이어 해결
32768 큐브의 앞면 이미지
중앙을 해결 한 다음 모서리를 해결 한 다음 가장자리를 해결합니다
센터는 각 단계가 특정 색상의 모든 조각을 한 얼굴에서 원하는 얼굴로 움직이는 15 단계로 해결됩니다. 예 : 무대는 흰색 얼굴의 모든 녹색 조각을 녹색 얼굴로 움직입니다. 모든 색상과 얼굴에 대해 이것을 반복하십시오.
솔버는 여기에 설명 된 정류기를 사용하여 얼굴의 한 사분면에서 다른 얼굴의 Quandrant까지 중앙 조각을 통근 할 수 있습니다. 이 정류기의 매우 중요한 속성은 많은 조각을 동시에 단일 줄로 움직일 수 있도록 수정할 수 있다는 것입니다. 매우 큰 큐브의 경우 이것은 단일 작업에서 수천 개의 조각이 아니라면 수백을 움직일 수 있음을 의미합니다. 평균 이동 수는 k = (2 * p + 5) / p입니다. 여기서 p는 작업 당 이동할 수있는 조각의 수입니다. K는 큐브 크기가 증가함에 따라 빠르게 2에 접근합니다.
모서리는 모서리를 제자리로 움직이고 얼굴이 올바르게 방향이 될 때까지 회전하는 기본적인 Brute Force 방법을 사용하여 해결됩니다. Will Smith는 다음과 같이 설명 할 수 있습니다 : https://www.youtube.com/watch?v=WBZKDRC9VQS
가장자리는 모든 모서리 쌍을 앞면으로 이동 한 다음 원하는 조각을 왼쪽 가장자리에서 오른쪽 가장자리로 바꾸어 해결합니다. 패리티 문제를 해결하거나 방지하는 데 필요한 여러 기능.
얼굴 회전은 본질적으로 무료입니다. 주어진 얼굴 (n^2 조각)의 모든 조각을 움직여 회전을 수행하는 대신 솔버는 단순히 얼굴을 읽고 쓰는 데 사용되는 좌표계를 변경합니다. 이로 인해 엄청난 양의 데이터 교환이 절약됩니다.
// Virtually rotate this face by q * 90 degrees
inline void Face::RotatefaceCW ( const int q)
{
orientation = (orientation + q) & 3 ;
}
// Gets the value of this face at coordinates r = row, c = column
inline const byte Face::GetRC ( const uint r, const uint c) const
{
switch (orientation) {
case 0 :
return data[(r << BS) + c];
case 1 :
return data[(c << BS) + (R1 - r)];
case 2 :
return data[((R1 - r) << BS) + (R1 - c)];
case 3 :
return data[((R1 - c) << BS) + r];
default :
return 0 ;
}
}이 코드에는 사용되는 간단한 이미지 수출 업체가 포함되어 있으며 각면을 이미지로 렌더링합니다.
https://www.nayuki.io/page/tiny-png output
https://github.com/nayuki/nayuki-web-published-code
Tiny PNG 출력은 C 및 C ++로 제공되는 작은 독립형 라이브러리로 RGB8.8.8 픽셀을 사용하여 PNG 파일을 씁니다.
총 이동 수는 간단한 공식을 사용하여 추정 할 수 있습니다. 큐브가 충분히 무작위 화되었다고 가정하면 첫 번째 얼굴이 1/6이 해결 될 것으로 예상 할 수 있으므로 조각의 5/6을 움직여야합니다. 두 번째 얼굴은 1/5를 해결하고 조각의 4/5를 움직여야합니다. 세 번째 얼굴은 3/4, 네 번째 얼굴 2/3, 다섯 번째 얼굴 1/2 및 마지막 얼굴은 완전히 해결됩니다. 단일 조각을 이동하기위한 평균 이동 수 (k)는 실험적으로 ~ 2.1로 추정 될 수 있습니다. 큐브의 크기가 증가함에 따라 k의 값은 감소합니다. 통근자가 각 조각을 최소 2 번 움직여야하기 때문에 값은 2 이상이 될 수 없습니다.
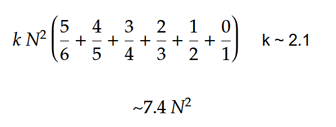
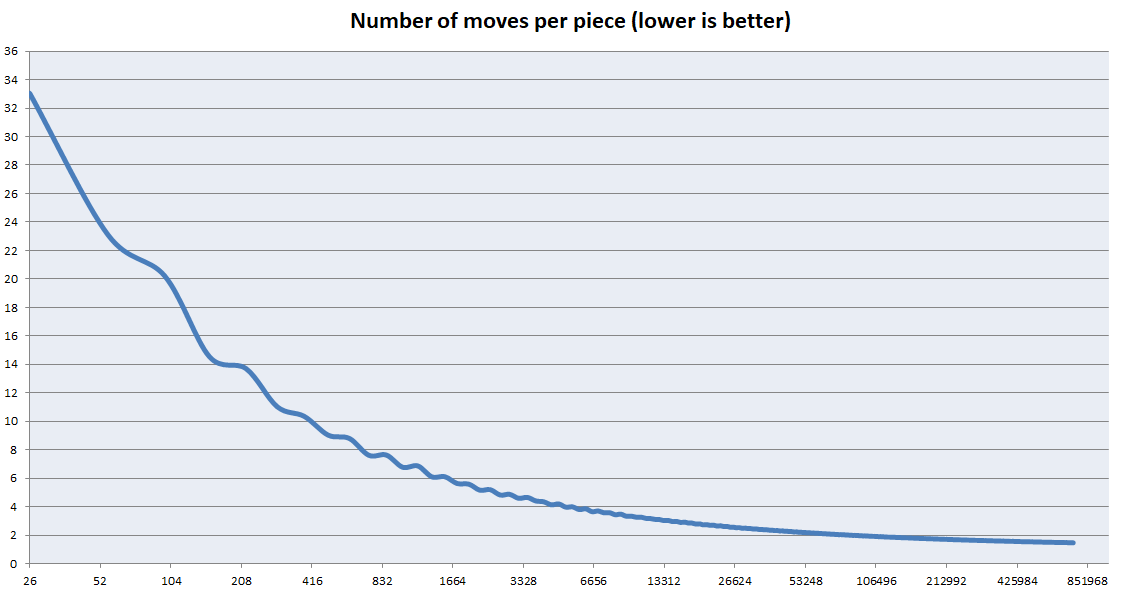
이 알고리즘은 매우 큰 큐브에 최적화되어 있습니다. 그러나 작은 큐브에는 끔찍합니다. 주요 최적화는 가능한 한 빨리 센터를 해결하는 데 중점을 두 었으며 가장자리를 해결하기 위해 고려하지 않았습니다. 그러나 가장자리의 크기는 큐브 크기가 증가함에 따라 중심에 비해 중요하지 않습니다. 아래 그래프는 더 큰 큐브로 피스 당 평균 이동 수가 어떻게 감소하는지 보여줍니다. 참고 : 이것은 k의 그래프가 아닙니다. (총 이동) / (조각 수)의 그래프입니다.
cmake -B build -S .
cd build
cmake --build .
RCube/RCube