equivalence testing multiple regression

다중 회귀에 대한 동등성 테스트

다중 회귀 모델에서 개별 예측 변수로부터의 관찰 된 효과가 통계적으로나 실질적으로 무시할 수있는 것으로 간주 될 정도로 적은지 평가하기 위해 동등성 테스트를 적용 할 수있다 (Alter & Counsell, 2021). 자세한 내용은 PSYARXIV에서 OSF 페이지 및/또는 자유롭게 사용할 수있는 사전 인쇄를 참조하십시오.

다음 기능은 다중 회귀에서 예측 변수와 결과 사이의 무시할 수있는 효과를 결론을 내릴 수있는 적절한 동등성 기반 대안을 제공합니다.

이러한 R 기능은 전체 데이터 세트에 대한 액세스 유무에 관계없이 여러 연구 컨텍스트를 쉽게 수용하도록 설계되었습니다. 두 기능인 reg.equiv.fd() 와 reg.equiv() 는 유사한 출력을 제공하지만 사용자가 요구하는 입력 정보 유형에 따라 다릅니다.

구체적으로, 첫 번째 함수 인 reg.equiv.fd() 는 r ( lm 객체)의 전체 데이터 세트와 모델이 필요하지만 두 번째는 그렇지 않습니다. reg.equiv() 전체 데이터 세트에 액세스 할 수 없지만 여전히 결과 섹션 또는 결과 섹션에 제시된 정보를 사용하여 다중 회귀에서 결과 변수와의 연관성 부족을 평가하려는 연구원을위한 것입니다. 테이블은 출판 된 기사에보고되었습니다.

reg.equiv.fd() : 전체 데이터 세트가 필요합니다

필수 입력 :

• datfra= 데이터 프레임 (예 : mtcars)
• model= 모델, LM 객체 (예 : mod1 , 여기서 mod1<- mpg~hp+cyl )
• delta= 가장 작은 효과 크기의 관심 크기 (Sesoi), 최소 의미있는 효과 크기 (MMES) 또는 등가 간격 (?) (예 : .15)의 상한.
• predictor= 테스트 할 예측 변수의 이름 (예 : "cyl" )

기본 설정 :

• test= 테스트 유형은 두 개의 일방적 인 테스트 (Tost; Schuirmann, 1987)로 자동으로 설정됩니다. 다른 옵션은 Anderson-Hauck (AH; Anderson & Hauck, 1983)입니다.
• std= 델타 (또는 sesoi)는 기본적으로 표준화 된 세트입니다. 표준화되지 않은 단위를 가정하기 위해 std=FALSE 나타냅니다
• alpha= 공칭 유형 I 오류율은 기본적으로 .05로 설정됩니다. 변경하려면 단순히 알파 레벨을 나타냅니다. 예 : alpha=.10

reg.equiv.fd() 예 :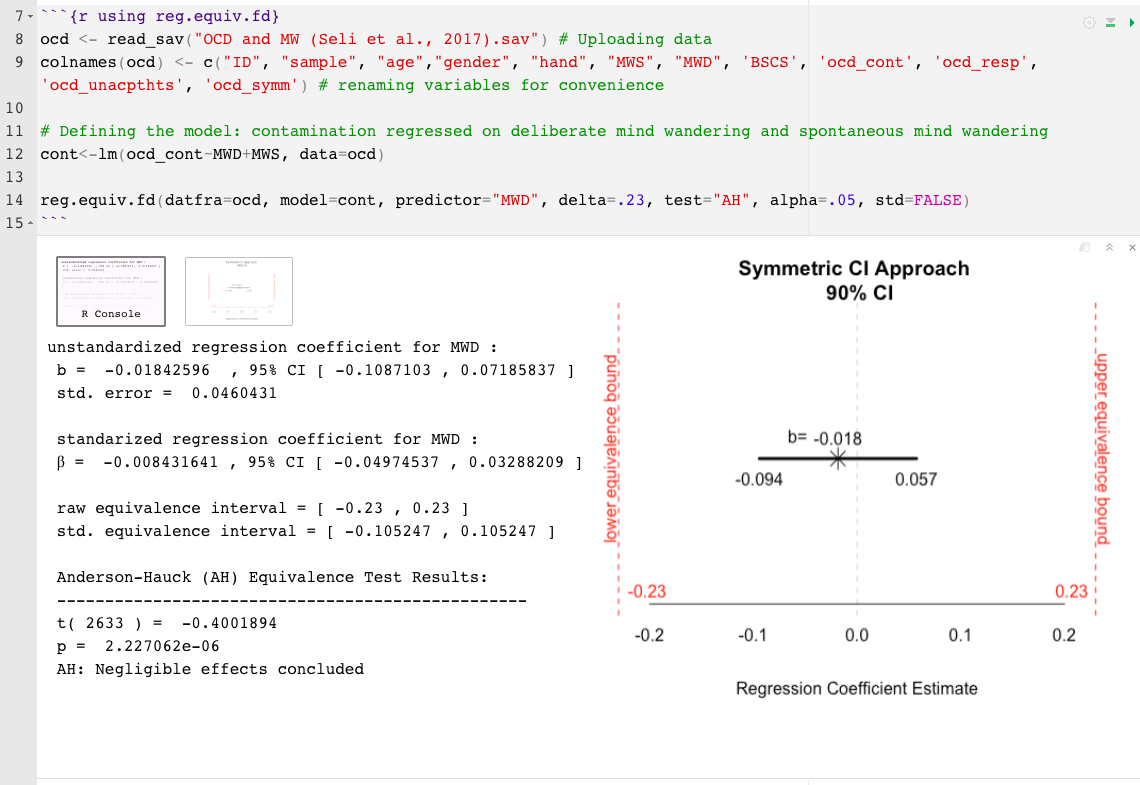

reg.equiv() : 전체 데이터 세트가 필요하지 않습니다

필수 입력 :

• b= 관심있는 예측 자와 관련된 추정 효과 크기는 표준화되거나 표준화되지 않을 수 있습니다 (예 : .02)
• se= 관심있는 예측 변수의 효과 크기와 관련된 표준 오차 (효과 크기가 표준화 된 경우 se 값이 표준화되지 않은 상태에서 원시 효과가 아닌지 확인하십시오).
• p= 회귀 모델의 총 예측 변수 수 (인터셉트 제외)
• n= 샘플 크기
• delta= 가장 작은 효과 크기의 관심 크기 (Sesoi), 최소 의미있는 효과 크기 (MMES) 또는 등가 간격 (?) (예 : .15)의 상한.
• predictor= 테스트 할 예측 변수의 이름 (예 : "cyl" )

기본 설정 :

• test= 테스트 유형은 두 개의 일방적 인 테스트 (Tost; Schuirmann, 1987)로 자동으로 설정됩니다. 다른 옵션은 Anderson-Hauck (AH; Anderson & Hauck, 1983)입니다.
• std= 델타 (또는 SESOI) 및 표시된 효과 크기는 기본적으로 표준화 된대로 설정됩니다. 표준화되지 않은 단위를 가정하기 위해 std=FALSE 나타냅니다
• alpha= 공칭 유형 I 오류율은 기본적으로 .05로 설정됩니다. 변경하려면 단순히 알파 레벨을 나타냅니다. 예 : alpha=.10

reg.equiv() 예 :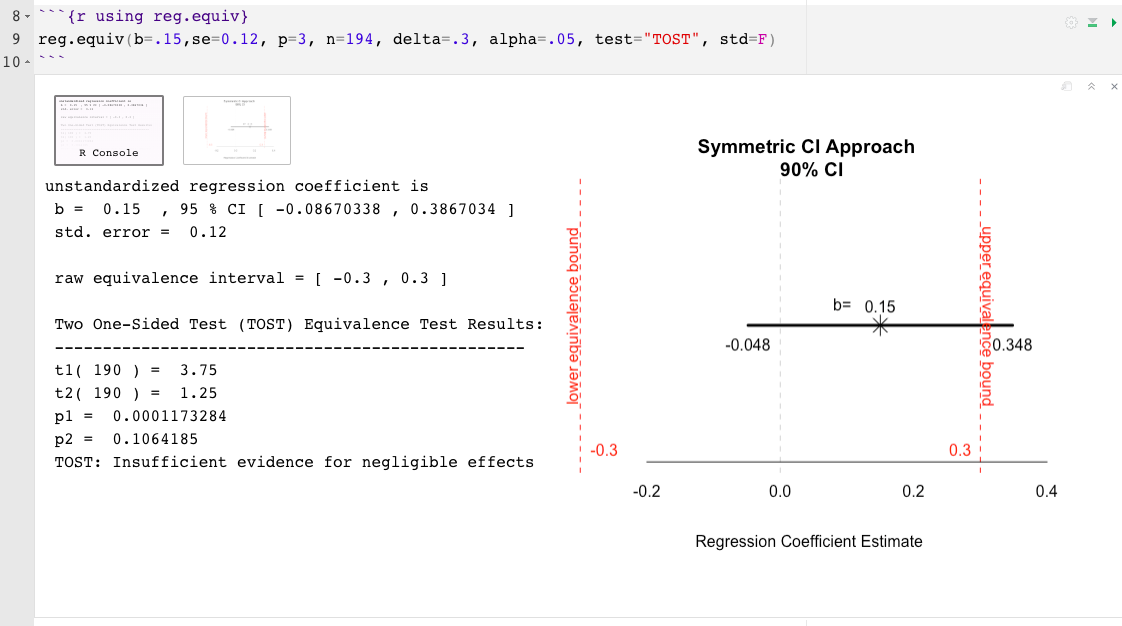

시험 결과 해석에 대한 권장 사항

동등성 테스트는 NHST (Null-Gysidesis Mightance Testing) 프레임 워크 내에서 설계된 방법입니다. NHST는 효과의 규모 또는 실습의 영향에 대한 고려가 거의 없거나 적은 P 값의 이분법적인 결과에 대한 과도한 비판을 받았다 (예 : G, Cumming, 2012; Fidler & Loftus, 2009; Harlow, 1997; Kirk, 2003; Lee, 2016). 연구원들은 NHST의 한계를 염두에두고 시험 결과의 실용적이고 통계적 측면을 풀어야합니다.

P 값의 한계를 최소화하기 위해,“무시할만한 효과”또는“무시할만한 효과에 대한 불충분 한 증거”의 결론을 넘어서 관찰 된 효과의 크기와 정밀도를 해석하는 것이 더 유익합니다. 관찰 된 효과는 동등성 경계, 불확실성의 정도 및 실질적인 영향 (또는 그 부족)과 관련하여 해석되어야합니다 . 이러한 이유로, 여기에 제공되는 두 개의 R 함수는 또한 관찰 된 효과의 그래픽 표현 및 동등성 간격과 관련된 관련 불확실성을 포함한다. 결과 플롯은 관찰 된 효과와 그 마진이 동등성 경계에서 얼마나 가까이 또는 넓거나 좁아지는 것을 보여줍니다. 동등성 간격과 관련하여 신뢰 대역의 비율과 위치에 대해 추론하면 p 값 이상의 결과를 해석하는 데 도움이 될 수 있습니다 .

심층적 인 문헌 검토, Disucsion, 권장 사항 및 자세한 자습서는 Alter & Counsell (2021)을 참조하십시오.

참조

1. Alter, U., & Counsell, A. (2021, 6 월 17 일). 다중 회귀에 대한 동등성 테스트 . https://doi.org/10.17605/osf.io/w96xe
2. Anderson, S., & Hauck, WW (1983). 비교 생체 이용률 및 기타 임상 시험에서 동등성을 테스트하기위한 새로운 절차. 통계 및 통신 이론 및 방법, 12 , 2663-2692. https://doi.org/10.1080/03610928308828634
3. Cumming, G. (2012). 새로운 통계 이해 : 효과 크기, 신뢰 구간 및 메타 분석 . 뉴욕, 뉴욕 : Taylor & Francis Group, LLC
4. Cumming, G. (2014). 새로운 통계 : 이유와 방법. 심리 과학, 25 (1), 7–29. https://doi.org/10.1177/095679613504966
5. Fidler, F., & Loftus, G. (2009). 오류 막대가있는 수치가 P 값을 대체 해야하는 이유 : 일부 개념적 논증과 경험적 데모. Zeitschrift für Psychologie/Journal of Psychology, 217 (1), 27-37. https://doi.org/10.1027/0044-3409.217.1.27
6. Harlow, LL (1997). 소개 및 개요의 중요성 테스트 . LL Harlow에서 Sa Muliak & JH Steiger (eds.). 중요성 테스트가 없다면 어떻게해야합니까? (pp.1-17). 미국 뉴저지 주 마와 : 로렌스 엘 바움.
7. Hauck, WW, & Anderson, S. (1984). 2 그룹 비교 생체 이용률 시험에서 동등성을 테스트하기위한 새로운 통계 절차. 약동학 및 바이오 제약 론지 저널, 12 (1), 83-91. https://doi.org/10.1007/BF01063612
8. Kirk, Re (2003). 효과 크기의 중요성 . SF Davis (ed.)에서 실험 심리학 연구 방법 핸드북 (pp. 83–105). MALDEN, MA : Blackwell.
9. Lee, DK (2016). P 값에 대한 대안 : 신뢰 구간 및 효과 크기. 한국의 마취학 저널, 69 (6), 555-562. https://doi.org/10.4097/kjae.2016.69.6.555
10. Schuirmann, DJ (1987). 평균 생체 이용률의 동등성을 평가하기위한 두 개의 단면 테스트 절차와 전력 접근법의 비교. 약동학 및 바이오 제약 론지 저널, 15 , 657-680. https://doi.org/10.1007/BF01068419
11. Seli, P., Risko, EF, Purdon, C., & Smilek, D. (2017). 침입적인 생각 : 자발적인 마음 방황 및 OCD 증상을 연결합니다. 심리 연구, 81 (2), 392-398. https://doi.org/10.1007/s00426-016-0756-3! 머지.