이 프로젝트는 Boost (Math/Direction/Autodiff)로 이동 했으며이 저장소는 더 이상 업데이트되지 않습니다.
| 나뭇가지 | 트래비스 | 앱베이어 | Codecov.io |
|---|---|---|---|
master | |||
develop |
AutoDiff는 단일 및 다중 변수의 수학적 함수의 자동 차별화 (전방 모드)를 용이하게하는 헤더 전용 C ++ 라이브러리입니다.
이 구현은 지점 x₀ 에서 분석 기능 F 의 Taylor 시리즈 확장을 기반으로합니다.
Autodiff의 필수 아이디어는 f (x₀) 의 평가에서 다항식으로 숫자를 대체하는 것입니다. 1 차 다항식 x₀+ε 로 x₀를 대체하고 동일한 알고리즘을 사용하여 f (x₀+ε)를 계산함으로써, ε 의 생성 된 다항식은 함수의 유도체 f '(x₀) , f' '(x₀) 를 포함합니다. , f '' ''(x ') , ... 계수 내. 각 계수는 해당 순서의 미분을 주문의 요인으로 나눈 것과 같습니다.
더 자세히 말해서, 하나는 x₀ 에서 f 의 첫 번째 n 미분을 계산하는 데 관심이 있다고 가정합니다. 미분 계산에 대한 정밀도의 손실없이, n 보다 큰 ε 의 전력을 포함하는 모든 용어 O (ε n+1 )를 폐기 할 수있다. (이는 다항식의 각 용어가 산술 연산 하에서 동일하고 하위 항에 의존한다는 사실 때문입니다.)이 절단 규칙에 따라, F는 다항식-폴리 alymial 변환을 제공합니다.
C ++의 연산자 및 기능을 과부하시키는 능력은 ε 의 다항식을 나타내는 클래스 fvar 의 생성을 허용합니다. 따라서 일반 (템플릿) 유형의 변수를 수락하고 반환하기 위해 작성 될 때 y₀ = f (x₀) 의 숫자 값을 계산하는 동일한 알고리즘 F는 다항식 ʃ n y n εⁿ = f (x₀+를 계산하는 데 사용됩니다. ε) . 유도체 f (n) (x₀) 는 각각의 팩토리 노트 n의 산물로부터 발견된다! 그리고 계수 y n :

#include <boost/math/direction/autodiff.hpp> #include <iostream> 템플릿 <typename t>
t Fourth_Power (t const & x) {
t x4 = x * x; // 연산자의 retval*()는 nrvo를 통해 x4의 메모리를 사용합니다.
x4 *= x4; // X4의 사본은 제곱이있을 때에도 연산자*= () 내에 만들어지지 않습니다.
반환 x4; // x4는 nrvo를 통해 main ()에서 y의 메모리를 사용합니다.} int main () {네임 스페이스 boost 사용 :: math :: 분화;
Constexpr 부호없는 순서 = 5; // 계산할 최고 순서 파생물.
자동 const x = make_fvar <double, order> (2.0); // x = 2에서 파생 상품을 찾으십시오.
자동 const y = fourth_power (x); for (서명되지 않은 i = 0; i <= order; ++ i)
std :: cout << "y.derivative ("<< i << ") ="<< y.derivative (i) << std :: endl; 반환 0;
}/*출력 : y.Derivative (0) = 16y.derivative (1) = 32y.derivative (2) = 48y.derivative (3) = 48y.derivative (4) = 24y.derivative (5) = 0*/위의 계산
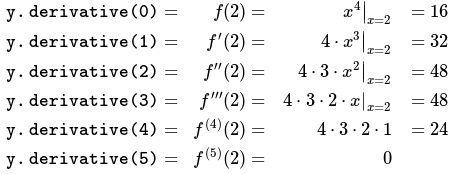
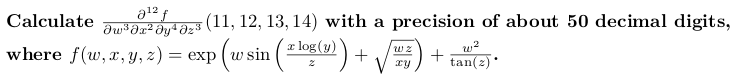
#include <boost/math/direciation/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <iostream> 네임 스페이스 boost :: math :: 차별화; 템플릿 <typename w, typename x, typename y, 타이프 이름 z>
<w, x, y, z> f (const w & w, const x & x, const y & y, const z & z) {네임 스페이스 std 사용;
return exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {float50 = boost :: multiprecision :: cpp_bin_float_50; constexpr nw = 3; // w에 대해 계산할 미분의 최대 순서
Constexpr 부호없는 NX = 2; // x를 계산할 미분의 최대 순서
constexpr signed ny = 4; // y를 계산할 미분의 최대 순서
Constexpr 부호없는 NZ = 3; // z에 대해 계산할 미분의 최대 순서
// 4 개의 독립 변수를 std :: 튜플로 선언합니다.
Auto Const 변수 = make_ftuple <float50, NW, NX, NY, NZ> (11, 12, 13, 14); Auto Const & w = std :: get <0> (변수); // w = 11에서 최대 NW 파생 상품
Auto Const & x = std :: get <1> (변수); // x = 12에서 최대 NX 파생 상품
Auto Const & y = std :: get <2> (변수); // y = 13에서 최대 NY 파생 상품
Auto Const & z = std :: get <3> (변수); // Z = 14에서 최대 뉴질랜드 파생 상품
자동 const v = f (w, x, y, z); // Mathematica 기호 분화에서 계산되었습니다.
Float50 Const Answer ( "1976.319600747797771777981875290418720908121189218755");
std :: cout << std :: setprecision (std :: numeric_limits <float50> :: digits10)
<< "Mathematica :"<< resond << 'n'<< "AutoDiff :"<< v.derivative (nw, nx, ny, nz) << 'n'<< std :: setprecision (3)
<< "상대적 오류 :"<< (v.derivative (nw, nx, ny, nz) / reson -1) << 'n'; 반환 0;
}/*Output:mathematica : 1976.3196007477977177798818752904187209081211892188autodiff : 1976.3196007477977177798818752904187209081211892188relative error: 2.67e-50*/ #include <boost/math/direciation/autodiff.hpp> #include <iostream> 네임 스페이스 사용 :: math :: 상수; 네임 스페이스 boost :: math :: 차별화; // 함수/변수 이름은 //입니다. https://en.wikipedia.org/wiki/greeks_(finance) #formulas_for_european_option_greeks// 표준 정상 누적 분포 함수관 <typename x>
x phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x);
} enum class cp {call, put}; // 0 연간 배당 수익률 (q = 0) .template <typename 가격, TypeName Sigma, typeName tau, typeName rate>를 가정합니다.
<Price, Sigma, Tau, rate> black_scholes_option_price 홍보 (CP CP, Double K,
Price Const & s,
Sigma Const & Sigma,
Tau Const & Tau,
rate const & r) {네임 스페이스 std 사용;
자동 const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (tau)); 자동 const d2 = (log (s / k) + (r -sigma * sigma / 2) * tau) / (Sigma * sqrt (tau)); 스위치 (cp) {case cp :: call : return s * phi (d1)-exp (-r * tau) * k * phi (d2); case cp :: put : return exp (-r * tau) * k * phi (-d2) -s * phi (-d1);
}
} int main () {Double Const K = 100.0; // 스트라이크 가격.
자동 const s = make_fvar <double, 2> (105); // 주가.
이중 Const Sigma = 5; // 변동성.
이중 const tau = 30.0 / 365; // 몇 년 안에 만료 시간. (30 일).
이중 const r = 1.25 / 100; // 금리.
Auto Const Call_Price = Black_Scholes_option_price (cp :: Call, K, S, Sigma, Tau, R); Auto Const put_price = black_scholes_option_price (cp :: put, k, s, sigma, tau, r);
std :: cout << "Black-scholes call price ="<< call_price.derivative (0) << 'n'<< "Black-scholes put price ="<< put_price.derivative (0) << 'n' << "Call delta ="<< call_price.derivative (1) << 'n'<< "put delta ="<< put_price.derivative (1) << 'n'<< "call gamma ="<< call_price .Edrivative (2) << 'n'<< "put gamma ="<< put_price.derivative (2) << 'n'; 반환 0;
}/*출력 : 검은 색 찰스 호출 가격 = 56.5136Black-scholes put price = 51.4109call delta = 0.773818put delta = -0.226182call gamma = 0.00199852 put gamma = 0.00199852*/더 큰 자동 계산 옵션 그리스인 목록은 예제/black_scholes.cpp를 참조하십시오.
위의 예는 Autodiff 사용의 장점 중 일부를 보여줍니다.
코드 중복 제거. 파생 상품을 계산하기위한 n 개의 별도의 기능의 존재는 코드 중복성의 형태이며, 모든 부채와 함께 제공됩니다.
한 기능으로 변경하려면 다른 기능에 대한 추가 변경 이 필요합니다. 위의 세 번째 예에서, 각 그리스 가치에 대해 별도의 함수가 작성된 경우 위의 코드베이스가 얼마나 크고 상호 의존적인지를 고려하십시오.
원래 함수의 변경이 이루어지면 다른 목적으로 파생 기능에 대한 종속성이 중단됩니다. 존재하지 않아도되는 것은 깨질 수 없습니다.
코드 블로트, 개념적 무결성 감소. 코드 기반이 더 작고 직관적으로 파악할 수있을 때 코드의 진화를 제어하는 것이 더 쉽고 안전합니다.
유한 한 차이 방법에 대한 파생 상품의 정확성. 단일-고정 유한 차이 방법에는 항상 각 응용 프로그램에 대해 신중하게 선택 해야하는 Δx 프리 변수가 포함됩니다. ΔX 가 너무 작 으면 숫자 오류가 커집니다. ΔX 가 너무 커지면 수학적 오류가 커집니다. AutoDiff를 사용하면 설정할 자유 변수가 없으며 ΔX 의 최상의 선택에도 불구하고 대답의 정확도는 일반적으로 유한 차이 방법보다 우수합니다.
추가 세부 사항은 Autodiff 매뉴얼에 있습니다.
Boost 소프트웨어 라이센스, 버전 1.0에 따라 배포됩니다.
헤더 전용.
C ++ 17에 최적화되었습니다. 또한 C ++ 11, C ++ 14로 컴파일하고 테스트하고 제안 된 C ++ 20 표준.
모든 메모리는 스택에 할당됩니다.
| 이름 | 목적 |
|---|---|
doc | 선적 서류 비치 |
example | 예 |
include | 헤더 |
test | 단위 테스트 |
보고 버그 : 사용중인 부스트 버전, 플랫폼 및 컴파일러를 언급하십시오. 문제를 재현하기위한 작은 편집 가능한 코드 샘플도 항상 좋습니다.
개발 지점에 대한 풀 요청으로 패치를 제출하십시오. 패치를 제출함으로써 귀하는 Boost 소프트웨어 라이센스, 버전 1.0에 따라 수정을 라이센스에 동의합니다.