최근에는 LLM(Large Language Model)이 다양한 분야에서 놀라운 능력을 보여주었지만, 수학적 추론 능력은 놀라울 정도로 약하다. Downcodes의 편집자는 산술 연산에서 LLM의 놀라운 "비밀"을 밝히는 최신 연구를 해석하고 이 방법의 한계와 향후 개선 방향을 분석합니다. 이 연구는 LLM의 내부 운영 메커니즘에 대한 이해를 심화시킬 뿐만 아니라 LLM의 수학적 능력을 향상시키는 데 귀중한 참고 자료를 제공합니다.
최근 AI 대형 언어 모델(LLM)은 시 쓰기, 코드 작성, 채팅 등 다양한 작업에서 뛰어난 성능을 발휘하고 있습니다. 하지만, 이 "천재" AI가 실제로는 "수학 신인"이라는 사실이 믿어지시나요? 간단한 산술 문제를 풀 때 종종 뒤집히는 경우가 있는데, 정말 놀랍습니다.
최근 연구에 따르면 LLM의 산술 추론 능력 뒤에 있는 "이상한" 비밀이 밝혀졌습니다. LLM은 강력한 알고리즘이나 기억에 의존하지 않고 "휴리스틱 잡다한"이라는 전략을 채택합니다. 이는 수학 공식과 정리를 진지하게 공부하지 않는 학생과 같습니다. 그러나 대답을 얻기 위해서는 "약간의 영리함"과 "경험의 법칙"에 의존합니다.
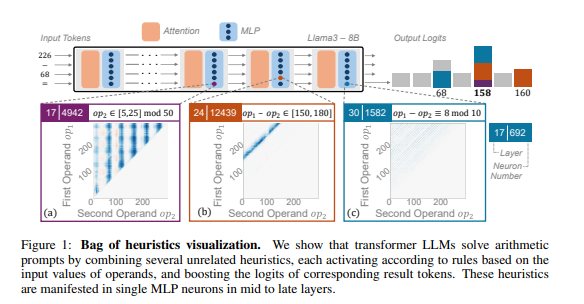
연구원들은 산술 추론을 일반적인 작업으로 사용했으며 Llama3, Pythia 및 GPT-J와 같은 여러 LLM에 대한 심층 분석을 수행했습니다. 그들은 산술 계산을 담당하는 LLM 모델 부분("회로"라고 함)이 많은 개별 뉴런으로 구성되어 있으며, 각 뉴런은 "소형 계산기"처럼 작동하고 특정 수치 패턴을 인식하고 해당 패턴을 출력하는 역할만 담당한다는 사실을 발견했습니다. 답변. 예를 들어, 한 뉴런은 "한 자리 숫자가 8인 숫자"를 식별하는 일을 담당할 수 있고, 다른 뉴런은 "결과가 150에서 180 사이인 빼기 연산"을 식별하는 일을 담당할 수 있습니다.
이러한 "미니 계산기"는 도구를 뒤섞은 것과 같으며 특정 알고리즘에 따라 사용하는 대신 LLM은 이러한 "도구"를 무작위로 조합하여 입력하는 숫자 패턴에 따라 답을 계산합니다. 정해진 레시피는 없지만 손에 잡히는 재료에 따라 마음대로 섞어서 마침내 '다크 요리'를 만드는 셰프와 같습니다.
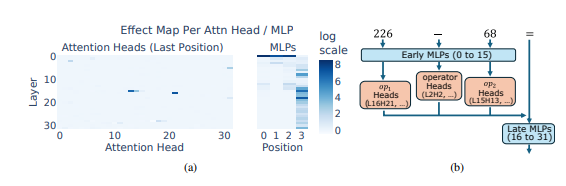
더욱 놀라운 점은 이러한 "휴리스틱 뒤죽박죽" 전략이 실제로 LLM 훈련 초기 단계에 나타났으며 훈련이 진행됨에 따라 점차 개선되었다는 점입니다. 이는 LLM이 이후 단계에서 이 전략을 개발하는 대신 처음부터 추론에 대한 이러한 "패치워크" 접근 방식에 의존한다는 것을 의미합니다.
그렇다면 이 "이상한" 산술 추론 방법은 어떤 문제를 일으킬까요? 연구자들은 "휴리스틱 잡다한" 전략이 일반화 능력이 제한적이고 오류가 발생하기 쉽다는 사실을 발견했습니다. LLM에는 "작은 영리함"의 수가 제한되어 있고, 이러한 "작은 영리함" 자체에도 새로운 수치 패턴을 접할 때 올바른 답을 제공하지 못하는 결함이 있을 수 있기 때문입니다. '토마토 스크램블 에그'밖에 만들 수 없는 셰프처럼, 갑자기 '생선맛 돼지고기'를 만들어 달라고 하면 당황할 수밖에 없을 것이다.
본 연구에서는 LLM의 산술추론 능력의 한계를 밝히고, 앞으로 LLM의 수학적 능력을 향상시킬 방향을 제시하였다. 연구원들은 기존 훈련 방법과 모델 아키텍처에만 의존하는 것만으로는 LLM의 산술 추론 능력을 향상시키기에 충분하지 않을 수 있으며, LLM이 진정한 "수학적 대가"가 될 수 있도록 보다 강력하고 일반적인 알고리즘을 학습할 수 있도록 새로운 방법을 모색해야 한다고 믿습니다.
논문 주소: https://arxiv.org/pdf/2410.21272
전체적으로 본 연구는 수학적 추론에서 LLM의 "이상한" 전략에 대한 심층 분석을 제공하고, LLM의 한계를 이해할 수 있는 새로운 관점을 제공하며, 향후 연구의 방향을 제시합니다. 저는 지속적인 기술 발전으로 LLM의 수학적 능력이 크게 향상될 것이라고 믿습니다.