

PyPortfolioOpt é uma biblioteca que implementa métodos de otimização de portfólio, incluindo técnicas clássicas de otimização de média-variância e alocação de Black-Litterman, bem como desenvolvimentos mais recentes na área, como redução e paridade de risco hierárquico.
É extenso , mas facilmente extensível , e pode ser útil tanto para investidores casuais quanto para profissionais que procuram uma ferramenta fácil de prototipagem. Quer você seja um investidor orientado aos fundamentos que identificou um punhado de escolhas subvalorizadas ou um trader algorítmico que possui uma cesta de estratégias, o PyPortfolioOpt pode ajudá-lo a combinar suas fontes alfa de maneira eficiente em termos de risco.
PyPortfolioOpt foi publicado no Journal of Open Source Software?
PyPortfolioOpt agora é mantido por Tuan Tran.
Acesse a documentação no ReadTheDocs para obter uma visão aprofundada do projeto ou confira o livro de receitas para ver alguns exemplos que mostram o processo completo, desde o download de dados até a construção de um portfólio.
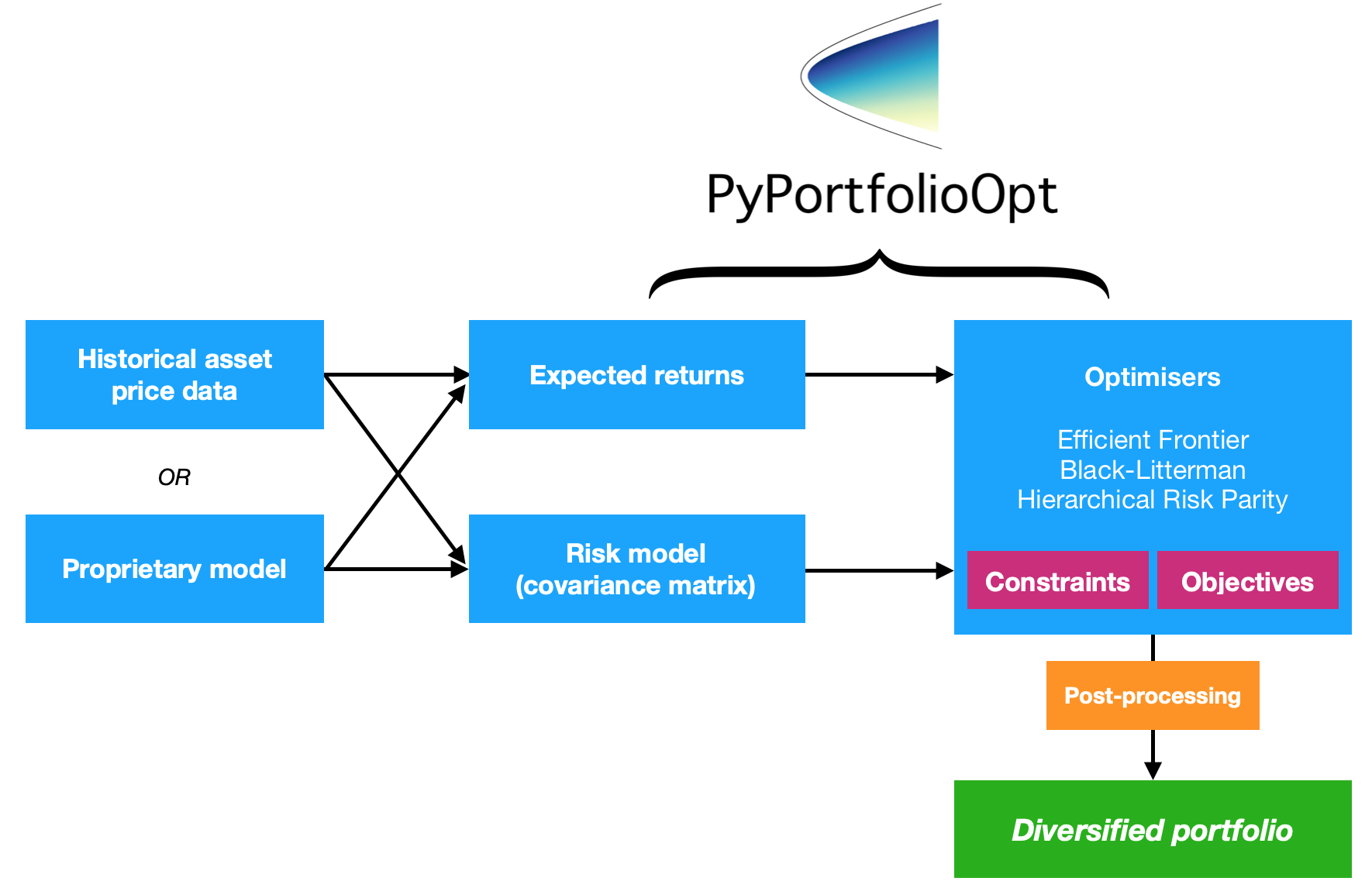
Se quiser brincar com PyPortfolioOpt interativamente em seu navegador, você pode iniciar o Binder aqui. A configuração demora um pouco, mas permite que você experimente as receitas do livro de receitas sem ter que lidar com todos os requisitos.
Nota: os usuários do macOS precisarão instalar ferramentas de linha de comando.
Nota: se você estiver no Windows, primeiro você precisa instalar o C++. (download, instruções de instalação)
Este projeto está disponível no PyPI, o que significa que você pode simplesmente:
pip install PyPortfolioOpt(pode ser necessário seguir instruções de instalação separadas para cvxopt e cvxpy).
No entanto, é uma prática recomendada usar um gerenciador de dependências em um ambiente virtual. Minha recomendação atual é preparar-se para a poesia e depois executar
poetry add PyPortfolioOptCaso contrário, clone/baixe o projeto e no diretório do projeto execute:
python setup.py install PyPortfolioOpt suporta Docker. Crie seu primeiro contêiner com docker build -f docker/Dockerfile . -t pypfopt . Você pode usar a imagem para executar testes ou até mesmo iniciar um servidor Jupyter.
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bashPara obter mais informações, leia este guia.
Se você gostaria de fazer grandes mudanças para integrar isso ao seu sistema proprietário, provavelmente faz sentido clonar este repositório e usar apenas o código-fonte.
git clone https://github.com/robertmartin8/PyPortfolioOptAlternativamente, você pode tentar:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.gitAqui está um exemplo de dados de ações da vida real, demonstrando como é fácil encontrar o portfólio long-only que maximiza o índice de Sharpe (uma medida de retornos ajustados ao risco).
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )Isso gera os seguintes pesos:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28Isto é interessante, mas não é útil por si só. No entanto, PyPortfolioOpt fornece um método que permite converter os pesos contínuos acima em uma alocação real que você pode comprar. Basta inserir os preços mais recentes e o tamanho de portfólio desejado (US$ 10.000 neste exemplo):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89Isenção de responsabilidade: nada neste projeto constitui conselho de investimento e o autor não se responsabiliza por suas decisões de investimento subsequentes. Consulte a licença para obter mais informações.
O artigo de Harry Markowitz de 1952 é o clássico inegável, que transformou a otimização de portfólio de uma arte em uma ciência. A principal conclusão é que, ao combinar activos com diferentes retornos e volatilidades esperados, pode-se decidir sobre uma alocação matematicamente óptima que minimize o risco de um retorno alvo – o conjunto de todas essas carteiras óptimas é referido como a fronteira eficiente .
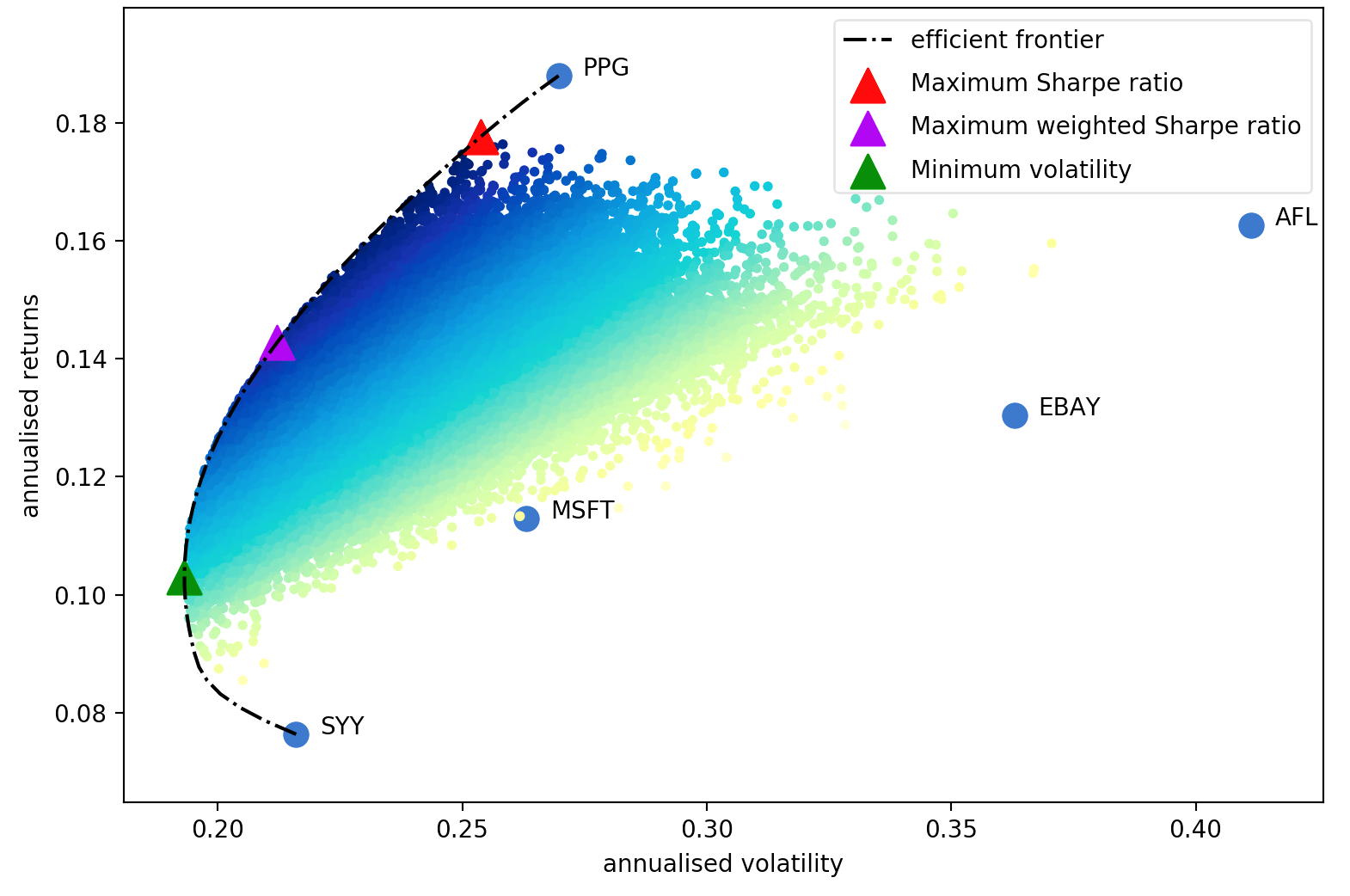
Embora muito desenvolvimento tenha sido feito no assunto, mais de meio século depois, as ideias centrais de Markowitz ainda são fundamentalmente importantes e são usadas diariamente em muitas empresas de gestão de portfólio. A principal desvantagem da otimização média-variância é que o tratamento teórico requer conhecimento dos retornos esperados e das características de risco futuras (covariância) dos ativos. Obviamente, se soubéssemos que os retornos esperados da vida das ações seriam muito mais fáceis, mas o jogo todo é que os retornos das ações são notoriamente difíceis de prever. Em alternativa, podemos derivar estimativas do retorno esperado e da covariância com base em dados históricos – embora percamos as garantias teóricas fornecidas por Markowitz, quanto mais próximas as nossas estimativas estiverem dos valores reais, melhor será a nossa carteira.
Assim, este projeto fornece quatro conjuntos principais de funcionalidades (embora, é claro, estejam intimamente relacionados)
Um objetivo principal do design do PyPortfolioOpt é a modularidade – o usuário deve ser capaz de trocar seus componentes enquanto ainda usa a estrutura fornecida pelo PyPortfolioOpt.
Nesta seção, detalhamos algumas das funcionalidades disponíveis do PyPortfolioOpt. Mais exemplos são oferecidos nos notebooks Jupyter aqui. Outro bom recurso são os testes.
Uma versão muito mais abrangente disso pode ser encontrada em ReadTheDocs, bem como possíveis extensões para usuários mais avançados.
A matriz de covariância codifica não apenas a volatilidade de um ativo, mas também como ele se correlaciona com outros ativos. Isto é importante porque, para colher os benefícios da diversificação (e assim aumentar o retorno por unidade de risco), os activos da carteira devem ser tão não correlacionados quanto possível.
sklearn.covariance .constant_variance , single_factor e constant_correlation .sklearn.covariance 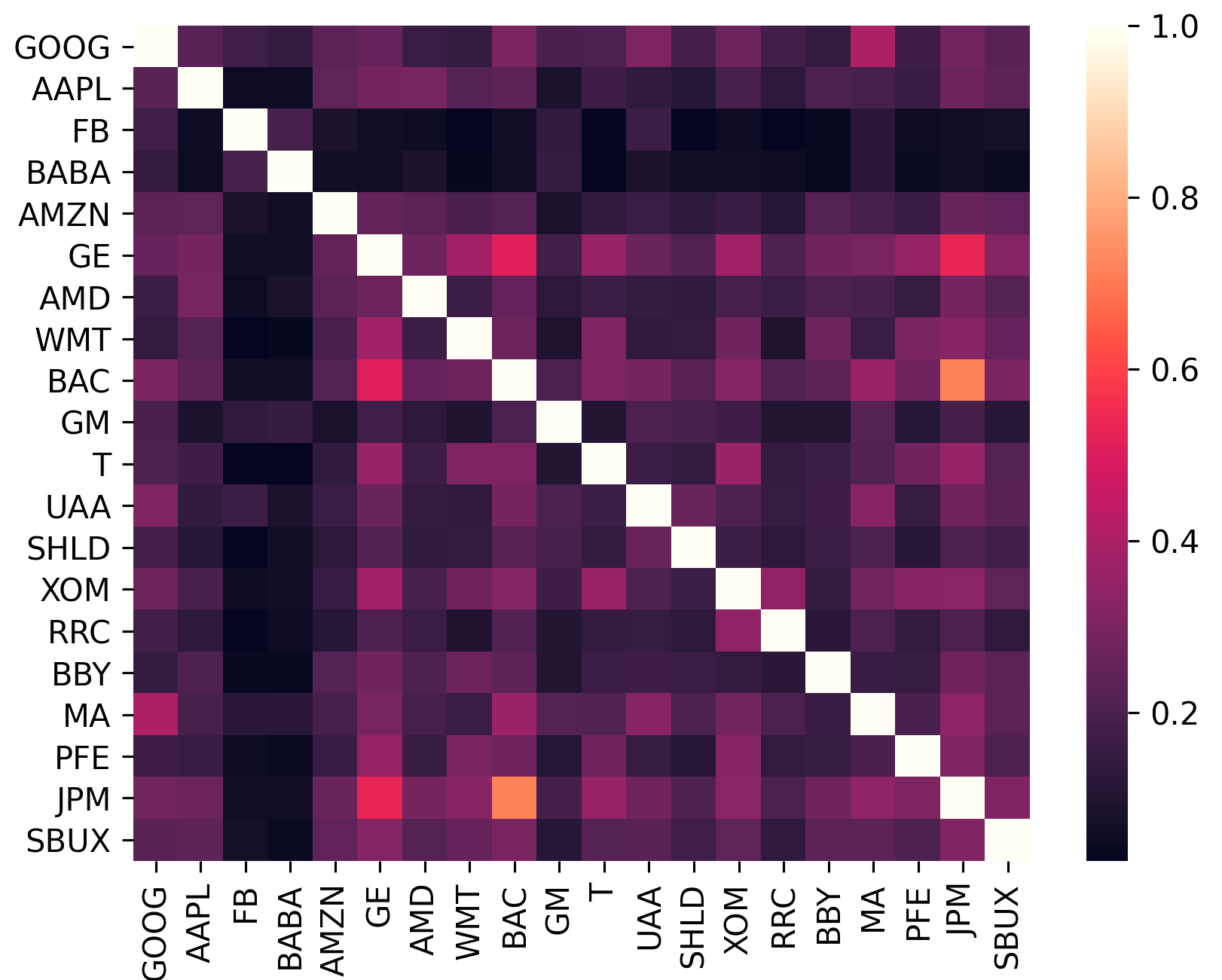
(Este gráfico foi gerado usando plotting.plot_covariance )
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk e efficient_return , PyPortfolioOpt oferece uma opção para formar uma carteira neutra para o mercado (ou seja, a soma dos pesos é zero). Isso não é possível para a carteira max Sharpe e a carteira min volatilidade porque, nesses casos, elas não são invariantes em relação à alavancagem. A neutralidade do mercado requer pesos negativos: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 )) Um problema com a otimização de média-variância é que ela leva a muitos pesos zero. Embora estes sejam "ótimos" na amostra, há um grande conjunto de pesquisas que mostram que esta característica leva as carteiras de média-variância a um desempenho inferior fora da amostra. Para esse fim, introduzi uma função objetivo que pode reduzir o número de pesos insignificantes para qualquer uma das funções objetivo. Essencialmente, ele adiciona uma penalidade (parametrizada por gamma ) em pesos pequenos, com um termo que se parece com a regularização L2 no aprendizado de máquina. Pode ser necessário tentar vários valores gamma para atingir o número desejado de pesos não desprezíveis. Para a carteira teste de 20 títulos, gamma ~ 1 é suficiente
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()A partir da versão 0.5.0, agora oferecemos suporte à alocação de ativos Black-Litterman, que permite combinar uma estimativa anterior de retornos (por exemplo, os retornos implícitos no mercado) com suas próprias visões para formar uma estimativa posterior. Isto resulta em estimativas muito melhores dos retornos esperados do que apenas usar o retorno médio histórico. Confira a documentação para uma discussão da teoria, bem como conselhos sobre formatação de entradas.
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe () Os recursos acima referem-se principalmente à resolução de problemas de otimização de média-variância por meio de programação quadrática (embora isso seja resolvido por cvxpy ). No entanto, também oferecemos diferentes otimizadores:
Consulte a documentação para obter mais informações.
Os testes são escritos em pytest (muito mais intuitivo que unittest e as variantes na minha opinião) e tentei garantir uma cobertura próxima de 100%. Execute os testes navegando até o diretório do pacote e simplesmente executando pytest na linha de comando.
PyPortfolioOpt fornece um conjunto de dados de teste de retornos diários para 20 tickers:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]Esses tickers foram selecionados informalmente para atender a vários critérios:
Atualmente, os testes não exploraram todos os casos extremos e combinações de funções e parâmetros objetivo. No entanto, cada método e parâmetro foram testados para funcionar conforme esperado.
Se você usa PyPortfolioOpt para trabalhos publicados, cite o artigo JOSS.
Sequência de citação:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
BibTex::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}Contribuições são muito bem-vindas . Dê uma olhada no Guia de Contribuição para mais informações.
Gostaria de agradecer a todas as pessoas que contribuíram para o PyPortfolioOpt desde o seu lançamento em 2018. Agradecimentos especiais para: