smard power forecasting
1.0.0
Este repositório é para prever o consumo de energia alemão.
Baseado e inspirado em:
Fonte de dados: SMARD
Coloque todos os arquivos baixados em:
/example/dataset # there is already used dataset included if you pull, but you could update
Verifique o arquivo forecast.Rmd para ver como você pode executar este código em uma versão atualizada do SMARD-Data.
Bibliotecas usadas:
# Probably needed
# Load Packages
# library(fhswf)
# library(tsibbledata)
# library(broom)
# library(readr)
# library(datasets)
# library(timeDate)
# library(qlcal)
# library(corrplot)
# library(mgcv)
# library(MEFM)
# library(TTR)
packages <- c(
"devtools",
"ggplot2",
"dplyr",
"tsibble",
"fable",
"fabletools",
"feasts",
"distributional",
"lubridate",
"tidyr",
"forecast",
"zoo",
"scales",
"fable.prophet"
)
install.packages(packages)
library(devtools)
library(ggplot2)
library(dplyr)
library(tsibble)
library(fable)
library(fabletools)
library(feasts)
library(distributional)
library(lubridate)
library(tidyr)
library(forecast)
library(zoo)
library(scales)
library(fable.prophet)
Tente trabalhar no exemplo/pasta para começar.
# Define datapaths
power_consum_path <- "dataset\stunde_2015_2024\Realisierter_Stromverbrauch_201501010000_202407090000_Stunde.csv"
power_consum_smard_prediction_path <- "dataset\propgnose_vom_smard\Prognostizierter_Stromverbrauch_202401010000_202407090000_Stunde.csv"
# Load Smard Prediction
power_consum_smard_prediction_loaded <- load_power_consum(path=power_consum_smard_prediction_path)
raw_smard_pred <- power_consum_smard_prediction_loaded$raw_data
cleaned_smard_pred <- power_consum_smard_prediction_loaded$cleaned_data
cleaned_smard_pred <- cleaned_smard_pred |>
mutate(.model = "SMARD")
names(cleaned_smard_pred)[names(cleaned_smard_pred) == "PowerConsum"] <- ".mean"
# Load PowerConsum Data
power_consum_loaded <- load_power_consum(path=power_consum_path)
raw_power_consum <- power_consum_loaded$raw_data
cleaned_power_consum <- power_consum_loaded$cleaned_data
# Generate more features
cleaned_power_consum$localName[is.na(cleaned_power_consum$localName)] = "Working-Day"
cleaned_power_consum$MeanLastWeek <- rollapply(cleaned_power_consum$PowerConsum, width = 24*8, FUN = function(x) mean(x[1:(24*8-25)]), align = "right", fill = NA)
cleaned_power_consum$MeanLastTwoDays <- rollapply(cleaned_power_consum$PowerConsum, width = 24*3, FUN = function(x) mean(x[1:(24*3-25)]), align = "right", fill = NA)
cleaned_power_consum$MaxLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) max(x[1:(24*2-25)]), align = "right", fill = NA)
cleaned_power_consum$MinLastOneDay <- rollapply(cleaned_power_consum$PowerConsum, width = 24*2, FUN = function(x) min(x[1:(24*2-25)]), align = "right", fill = NA)
Os seguintes recursos foram gerados a partir do conjunto de dados e da API Holiday:
| Índice | Nome da coluna | Descrição |
|---|---|---|
| 1 | DataDe | Para validação de DateIndex (semelhante, mas bruto) |
| 2 | PowerConsum | Consumo de energia em MW |
| 3 | Índice de data | Carimbo de data e hora (aaaa-mm-dd hh:mm:ss) |
| 4 | Dia da semana | Mo, Di, Mi, Do, Fr, Sa, So (dias da semana em alemão) |
| 5 | Data | Data (aaaa-mm-dd) |
| 6 | Ano | Ano aaaa |
| 7 | Semana | Número da semana 0-53 |
| 8 | Hora | Número da hora 0-24 |
| 9 | Mês | Mês número 1-12 |
| 10 | nome local | Nome de um feriado para carimbo de data/hora |
| 11 | Dia de trabalho | 1/0 Se dia útil (Werktag) então 1 |
| 12 | Mo | 1/0 Se segunda-feira então 1 |
| 13 | Di | 1/0 Se terça-feira então 1 |
| 14 | Mi | 1/0 Se quarta-feira então 1 |
| 15 | Fazer | 1/0 Se quinta-feira então 1 |
| 16 | Padre | 1/0 Se sexta-feira então 1 |
| 17 | Sá | 1/0 Se sábado então 1 |
| 18 | Então | 1/0 Se for domingo, então 1 (não é necessário, se for usado de segunda a sábado) |
| 19 | Feriado | 1/0 Se for feriado então 1 |
| 20 | Dia útilFeriadoFim de semana | Se for Feriado, Final de Semana ou Dia Útil (para Parcelas é Char.) |
| 21 | Feriado e Dia de Trabalho | 1/0 Se o feriado for em dia útil então 1 |
| 22 | Último dia não foi dia de trabalho | 1/0 Se o último dia não foi um dia útil, então 1 |
| 23 | LastDayWasNotWorkDayAndNowWorkDay | 1/0 Se o último dia não foi um dia útil e agora é um dia útil, então 1 |
| 24 | NextDayIsNotWorkDayAndNowWorkDay | 1/0 Se o dia seguinte não for um dia útil e agora for um dia útil, então 1 |
| 25 | LastDayWasHolidayAndNotWeekend | 1/0 Se o último dia foi feriado e não fim de semana então 1 |
| 26 | NextDayIsHolidayAndNotWeekend | 1/0 Se o dia seguinte for feriado e não fim de semana então 1 |
| 27 | NomeDoFeriado | semelhante a localName (Nome do feriado) |
| 28 | Fim do ano | 1/0 Se for final do ano (Semana 52 ou 53) |
| 29 | PrimeiraSemanaDoAno | 1/0 Se for início do ano (Semana 1) |
| 30 | Feriado Prolongado | 1/0 Feriado atrasado (6 horas no dia seguinte) |
| 31 | Feriado Suavizado | HolidayExtend + sin(2*pi(Hora)+1)/24) |
| 32 | Média da última semana | Consumo médio de energia da semana passada (turno: 24*8-25) |
| 33 | MédiaLastTwoDays | Média de PowerConsum dos últimos dois dias (Shift: 24*3-25) |
| 34 | MaxLastOneDay | Max PowerConsum do último dia (Turno: 24*2-25) |
| 35 | MinLastOneDay | Min PowerConsum do último dia (Turno: 24*2-25) |
Neste estudo há um conjunto de dados do SMARD para o consumo de energia na Alemanha para os anos 2015-2024.
A Figura 1 mostra o conjunto de dados brutos com valores ausentes (vermelho), carimbos de data/hora duplicados (vermelho escuro) e consumo de energia ao longo do tempo (cinza), resolução horária. Com um valor ausente e uma duplicata por ano, foi fácil limpar o conjunto de dados. No geral, um conjunto quase limpo. Depois de limpar o conjunto de dados, existem observações plausíveis para o consumo de energia:
Existe uma abordagem simples para preencher as lacunas através da última observação (possível, porque a resolução é grande o suficiente e porque existem poucos valores faltantes). O primeiro valor foi mantido para duplicatas.
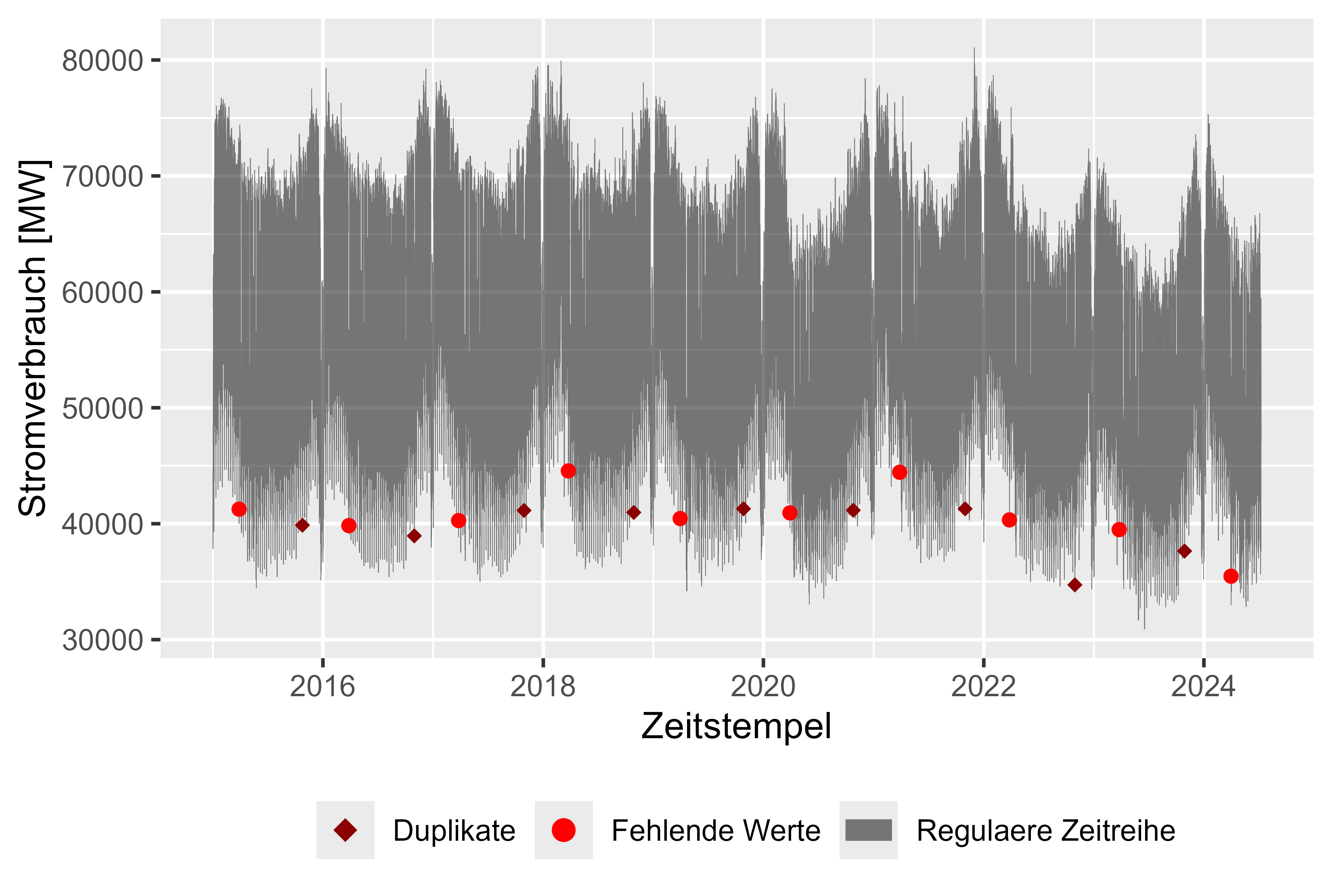Figura 1 Consumo de energia bruta
local_name_colors <- c(
"Christi Himmelfahrt" = palette()[2],
"Erster Weihnachtstag" = palette()[2],
"Karfreitag" = palette()[2],
"Neujahr" = palette()[2],
"Ostermontag" = palette()[2],
"Pfingstmontag" = palette()[2],
"Reformationstag" = palette()[2],
"Tag der Arbeit" = palette()[2],
"Tag der Deutschen Einheit" = palette()[2],
"Zweiter Weihnachtstag" = palette()[2],
"Regulärer Tag" = palette()[1]
)
week_colors <- c(
"Mo" = palette()[1],
"Di" = palette()[1],
"Mi" = palette()[1],
"Do" = palette()[1],
"Fr" = palette()[1],
"Sa" = palette()[2],
"So" = palette()[2]
)
working_colors <- c("1" = "#2E9FDF", "0" = "#FC4E07")
whw_colors <- c(
"FeiertagnKein Wochenende" = "black",
"Kein FeiertagnKein Wochenende" = "red",
"Kein FeiertagnWochenende" = "orange",
"FeiertagnWochenende" = "blue"
)
p <- cleaned_power_consum |>
gg_tsdisplay(PowerConsum, plot_type = "partial", lag = 100)
ggsave(
"plots/power_consum_acf_pacf.png",
plot = p,
width = 5.5,
height = 3.7,
dpi = 600
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MinLastOneDay.png",
x = "MinLastOneDay",
y = "PowerConsum",
x_label = "Minimaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MaxLastOneDay.png",
x = "MaxLastOneDay",
y = "PowerConsum",
x_label = "Maximaler Stromverbrauch vom letzten Tag [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastWeek.png",
x = "MeanLastWeek",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 7 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_calculated_features(
cleaned_power_consum = cleaned_power_consum,
file_name = "plots/MeanLastTwoDays.png",
x = "MeanLastTwoDays",
y = "PowerConsum",
x_label = "Durchschnittlicher Stromverbrauch der letzten 2 Tage [MW]",
y_label = "Stromverbrauch [MW]"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkdayHolidayWeekend",
file_name = "plots\workday_holiday_weekend_histogram.png",
colors = whw_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Feiertage",
name_1 = "Werktag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "Holiday",
file_name = "plots\holiday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Werktag oder Wochenende",
name_1 = "Feiertag"
)
plot_histogram_by_group(
cleaned_power_consum,
group_name = "HolidayAndWorkDay",
file_name = "plots\holiday_workday_histogram.png",
colors = working_colors,
x="PowerConsum",
x_label = "Stromverbrauch [MW]",
y_label = "Häufigkeit",
name_0 = "Wochenende oder Werktag",
name_1 = "Feiertag am Werktag"
)
plot_by_group(
cleaned_power_consum,
group_name = "HolidayName",
file_name = "plots\holiday_boxplot.png",
colors = local_name_colors,
title = "Übersicht der einzelnen Feiertage",
y="PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "Weekday",
file_name = "plots\weekday_boxplot.png",
colors = week_colors,
title = "Übersicht der einzelnen Wochentage",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_group(
cleaned_power_consum,
group_name = "WorkDay",
file_name = "plots\workday_boxplot.png",
colors = working_colors,
title = "Übersicht, ob Feiertag (FALSE) oder Werktag (TRUE)",
y = "PowerConsum",
y_label="Stromverbrauch [MW]",
x_label="Jahre"
)
plot_by_column(
df = cleaned_power_consum,
x = "Hour",
y = "PowerConsum",
x_label = "Stunden",
y_label = "Stromverbrauch [MW]",
file_name = "plots\hour_boxplot.png",
title = "Übersicht der einzelnen Stunden"
)
plot_by_column(
df = cleaned_power_consum,
x = "Month",
y = "PowerConsum",
x_label = "Monate",
y_label = "Stromverbrauch [MW]",
file_name = "plots\month_boxplot.png",
title = "Übersicht der einzelnen Monate"
)
plot_by_column(
df = cleaned_power_consum,
x = "Week",
y = "PowerConsum",
x_label = "Woche",
y_label = "Stromverbrauch [MW]",
file_name = "plots\week_boxplot.png",
title = "Übersicht der einzelnen Wochen"
)
plot_by_column(
df = cleaned_power_consum,
x = "Year",
y = "PowerConsum",
x_label = "Jahr",
y_label = "Stromverbrauch [MW]",
file_name = "plots\year_boxplot.png",
title = "Übersicht der einzelnen Jahre"
)
plot_year_month_week_day(
df=cleaned_power_consum,
date_column="DateIndex",
y="PowerConsum",
from_year=2015,
to_year=2024,
from_week=0,
to_week=53,
year_for_week=2018,
from_day=1,
to_day=30,
month_for_day=4,
year_for_day=2018,
from_month=1,
to_month=12,
year_for_month=2018,
holiday="Holiday",
day_of_week = "Weekday"
)
As seções a seguir detalharão cada vez mais os dados. Começaremos aqui com a representação anual.
A Figura 2 é a representação anual dos anos 2015-2024. Podemos notar aqui que no início do ano há um aumento no consumo de energia e no final do ano há uma diminuição (Natal, Ano Novo). No geral, parece um formato de sorriso ou um arco.
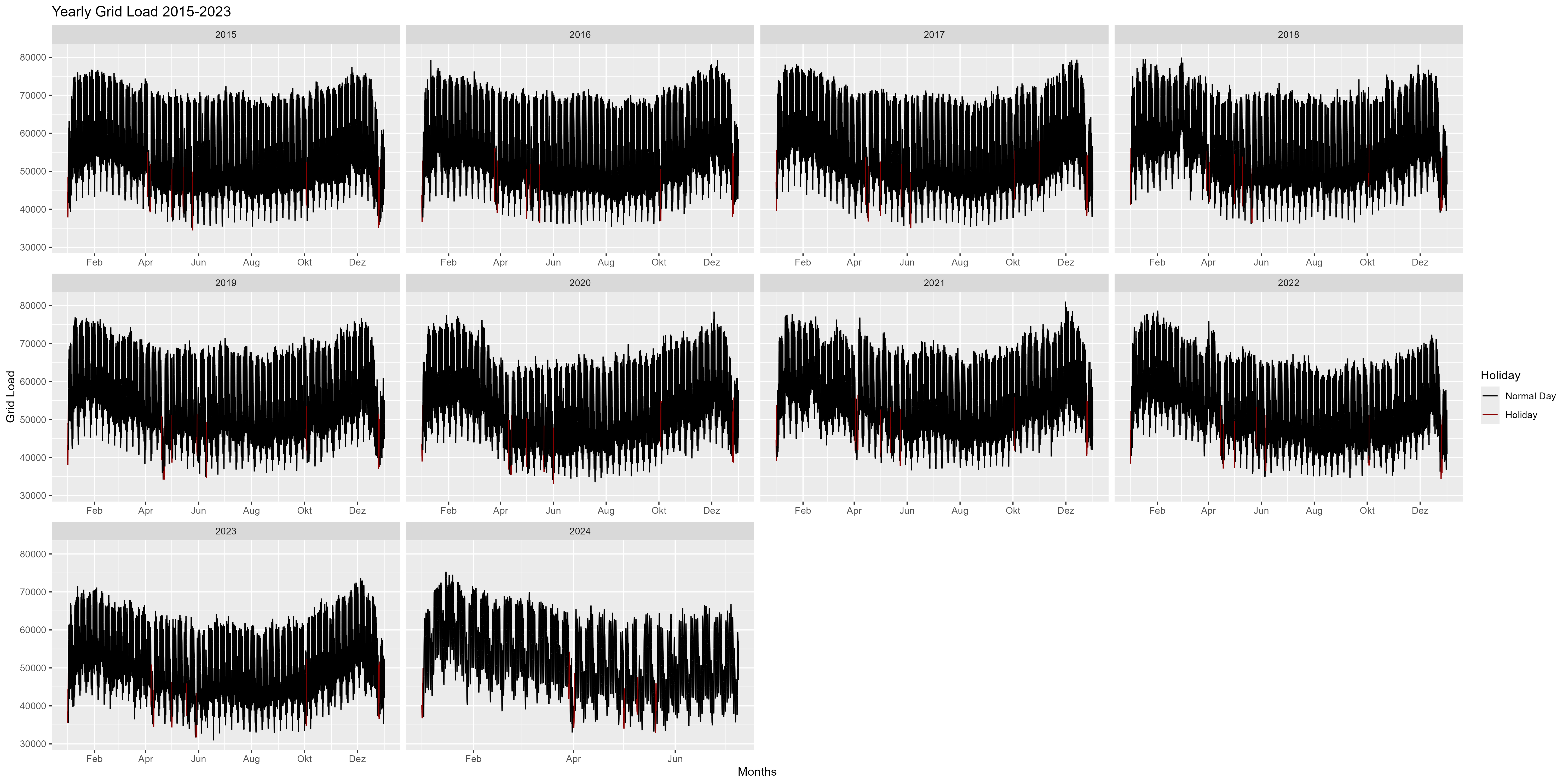Figura 2 Consumo de energia, todos os anos como uma faceta única
Vamos tentar agregar todos os anos e dividi-los em semanas. Os boxplots da Figura 3 combinam todos os anos. Podemos ver o padrão com mais detalhes. O início e o final do ano são representados em vermelho e mostram uma diminuição em relação ao "formato de sorriso" regular.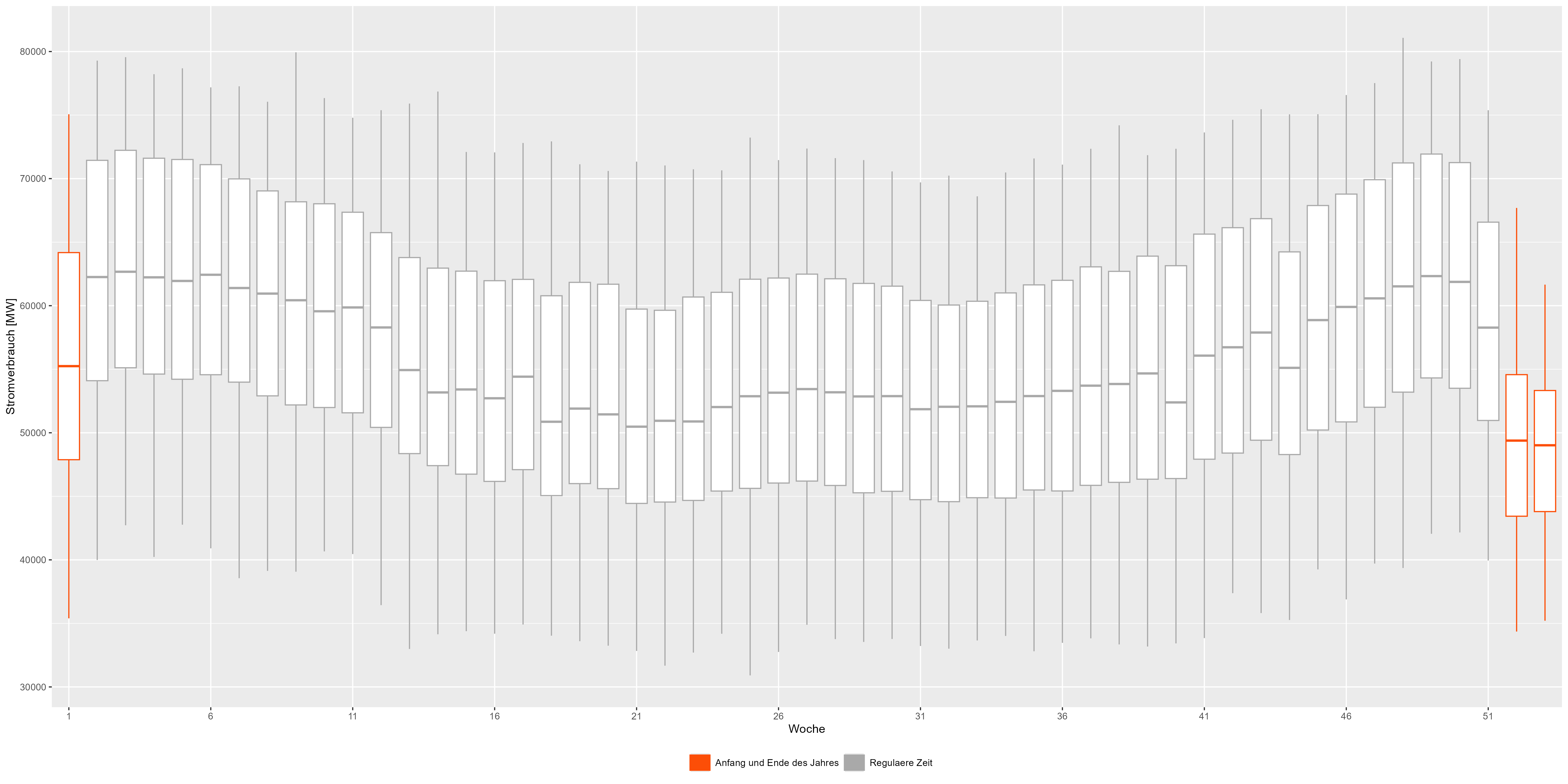
Figura 3 Dados agregados semanais de consumo de energia
Vamos detalhar mais e olhar para o ano de 2018, por exemplo. A Figura 4 é a representação mensal do ano de 2018. Aqui podemos observar com mais detalhes o final do ano. Por volta do dia 24 de Dezembro, verifica-se uma diminuição do consumo de energia. Também se destacam aqui os finais de semana e feriados (vermelho). Uma redução para todos os fins de semana e para todos os feriados.
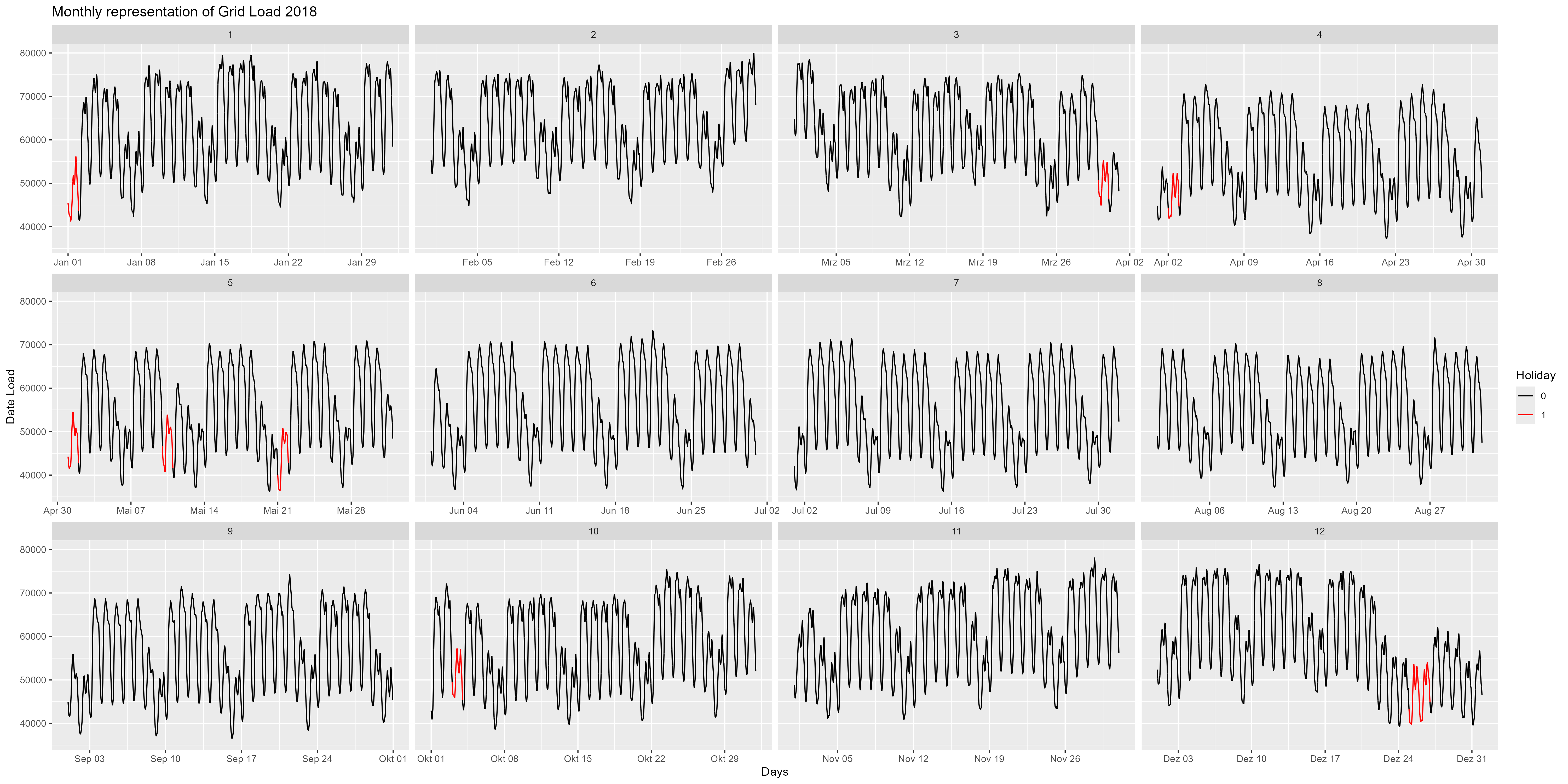Figura 4 Consumo de energia, todos os meses como uma faceta única
Poderíamos ir ainda mais longe e verificar a representação horária dos dados. A Figura 5 mostra o boxplot agregado para cada hora. Verifica-se também uma diminuição do horário noturno (21h00-06h00) e um aumento do horário diurno/laboral (06h00-21h00). Também é um padrão que precisa ser incluído no modelo.
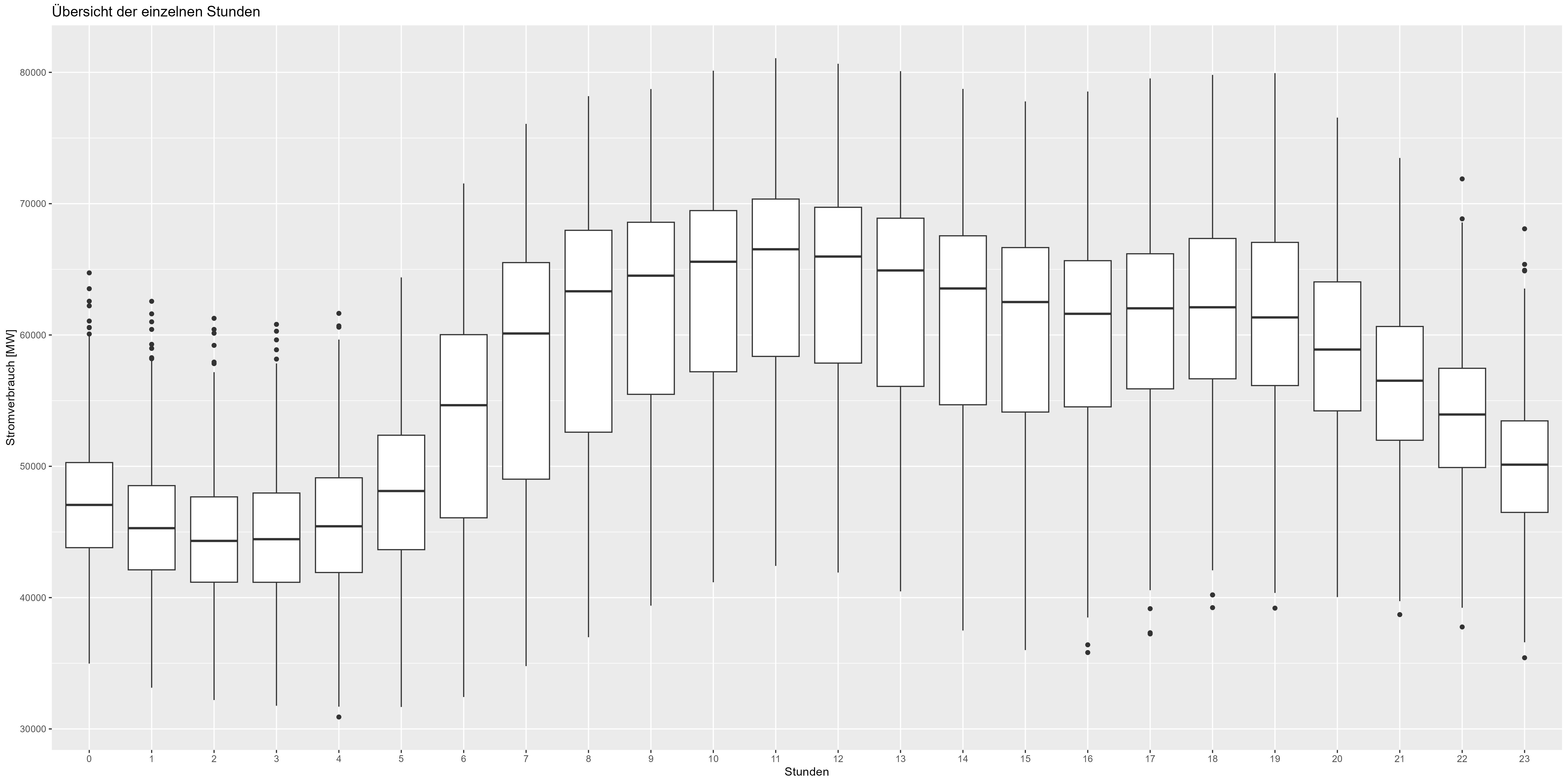Figura 5 Dados agregados de consumo de energia por hora
Vamos falar sobre os dias de semana. Como esperado no fim de semana o consumo de energia diminui. "Durchschnitt" é o meio. A Figura 6 mostra todos os dias da semana (agregados) ao longo dos anos. Há uma redução de ~10.000 MW nos finais de semana.
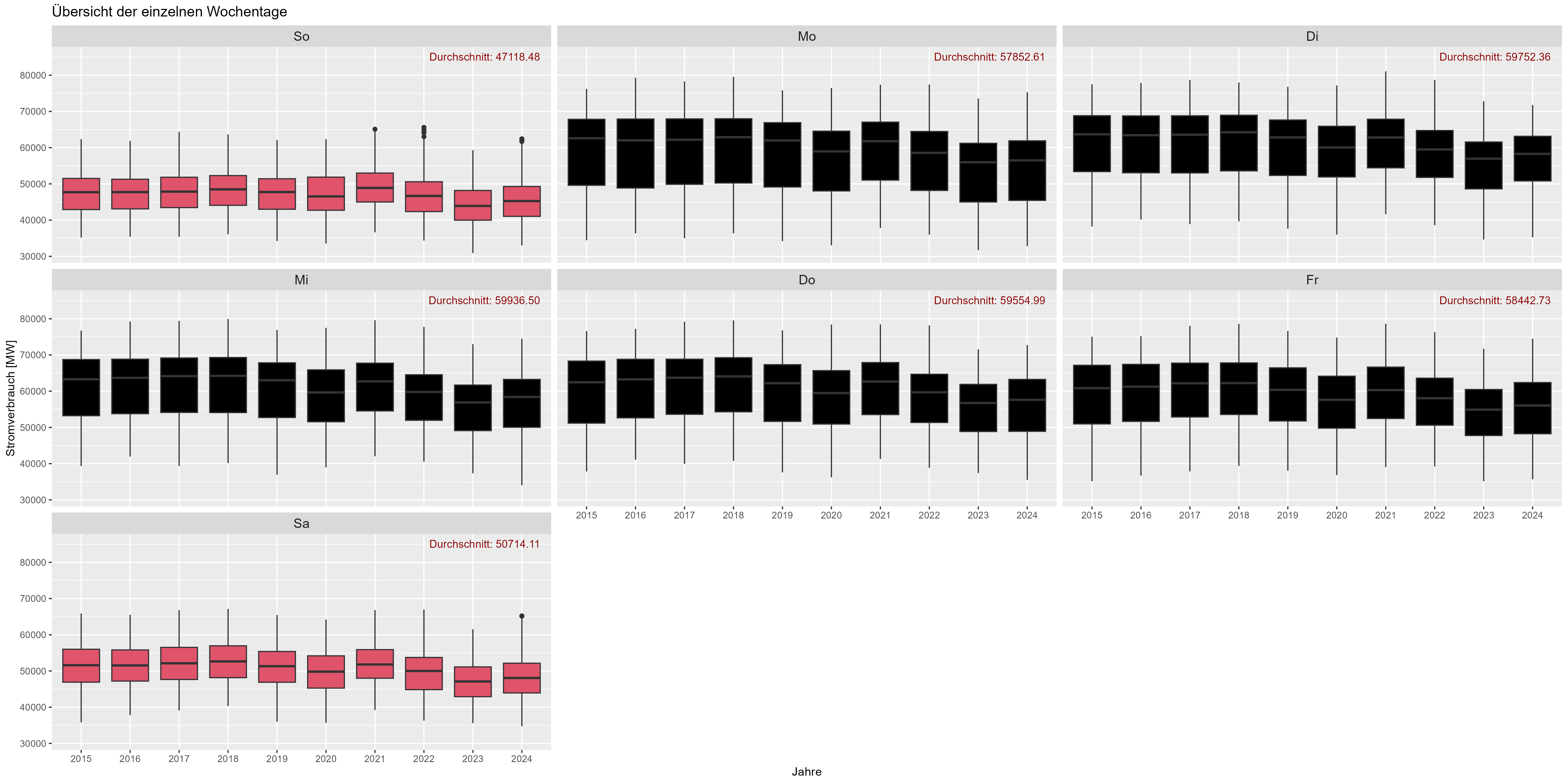Figura 6 Consumo de energia "efeito dia da semana"
A Figura 8 mostra o efeito feriado. "Durchschnitt" é o consumo médio de energia ao longo dos anos. Há um aumento significativo no consumo de energia para “Dias Úteis” (cinza escuro) em comparação com feriados (vermelho). Poderíamos assumir aqui que os feriados funcionam como fins de semana para o consumo de energia”.
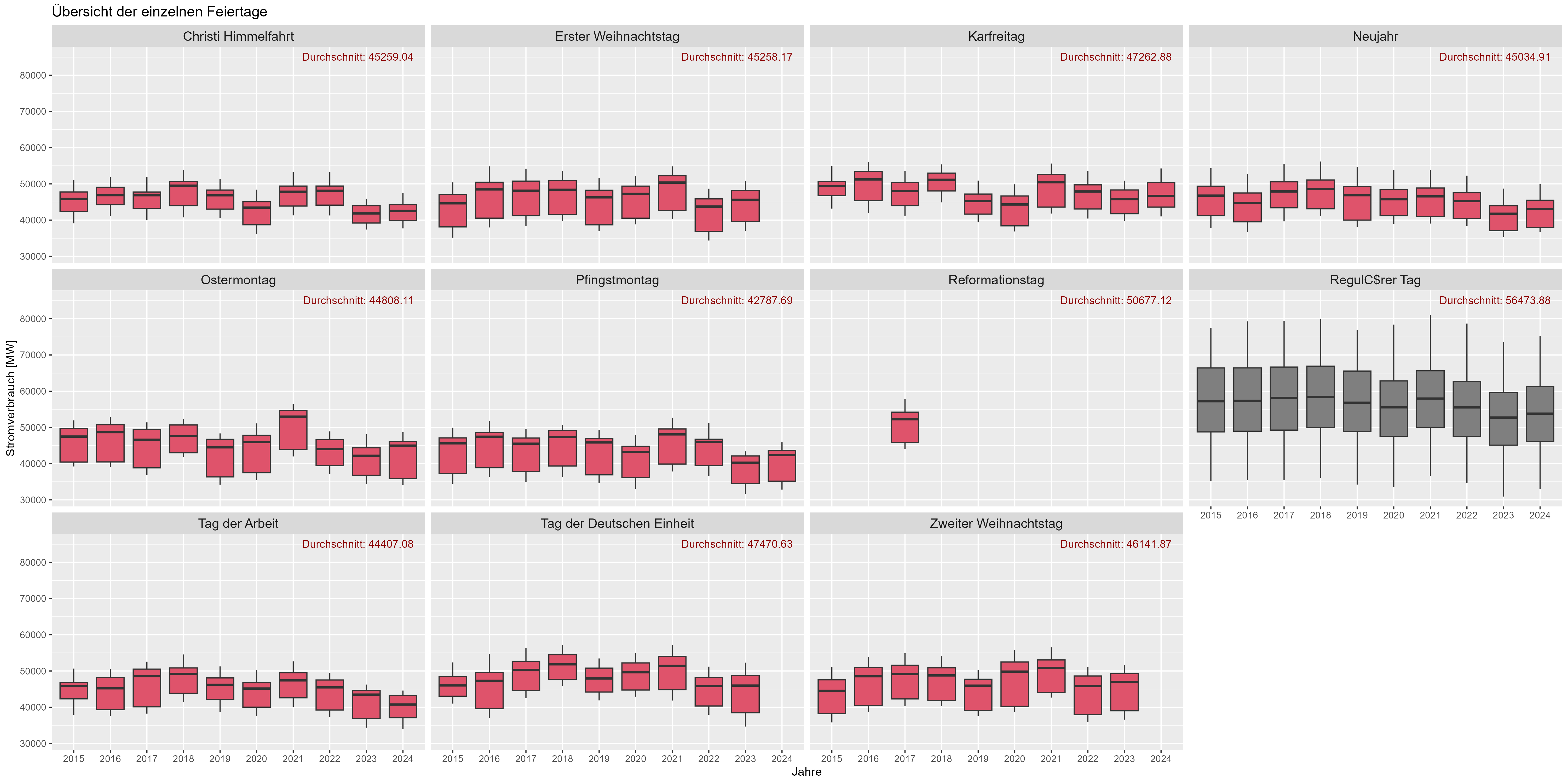Figura 6 Consumo de energia “efeito feriado”
A Figura 7 representa comportamentos diferentes para dias diferentes. Existem 4 categorias. "Feiertag Kein Wochenende" significa que é feriado, mas não fim de semana. "Feiertag Wochenende" significa que é feriado e fim de semana. "Kein Feiertag Kein Wochenende" significa que é um dia normal de trabalho e "Kein Feiertag Wochenende" significa que é apenas fim de semana. Podemos observar distribuições semelhantes para dias úteis não regulares, conforme assumido.
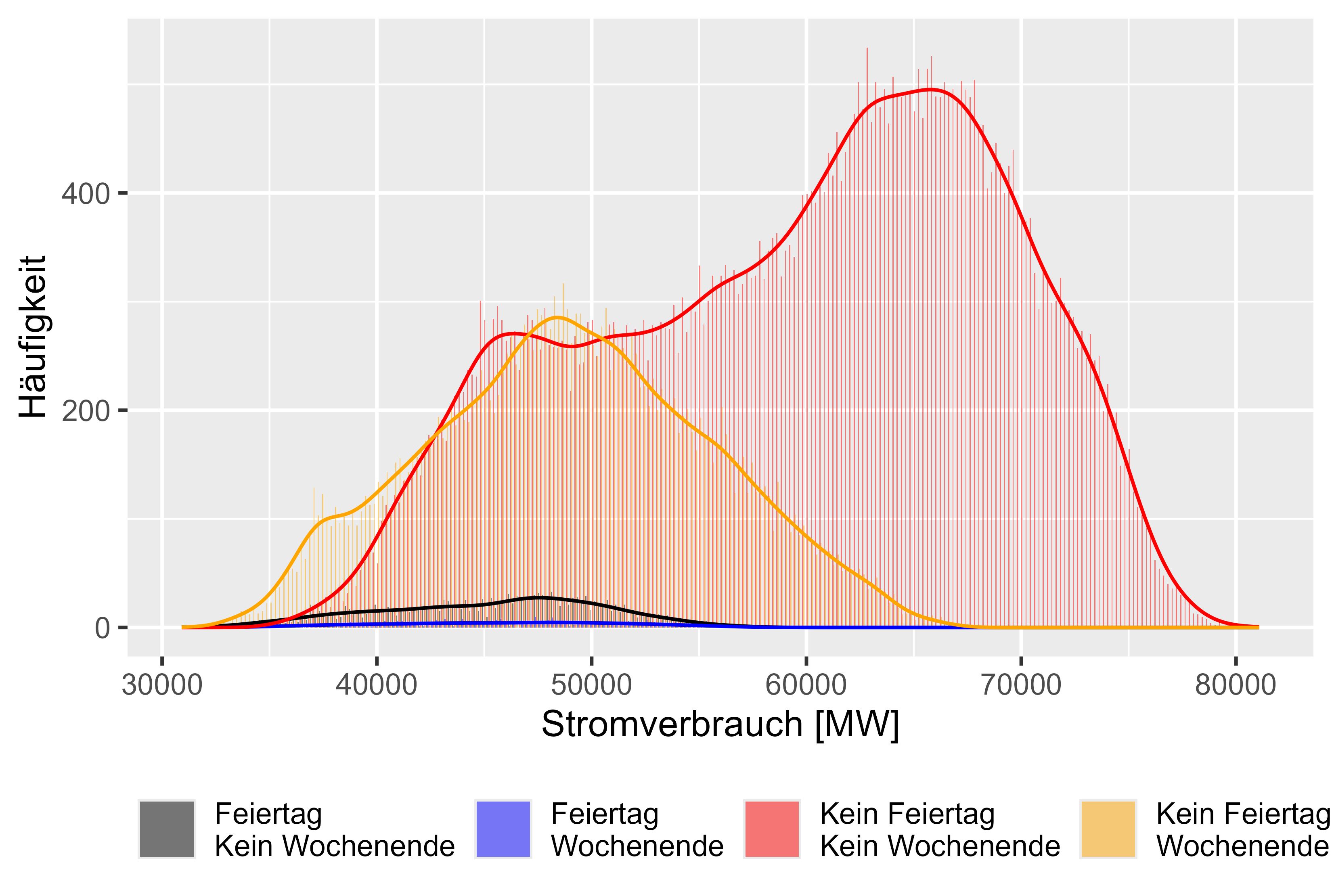Figura 7 Consumo de energia "Efeitos Diferentes" comparado
Valores defasados como MeanLastTwoDays, MeanLastWeek, MaxLastOneDay e MinLastOneDay são recursos gerados.
Semelhante ao discutido em DOI: 10.1109/TPWRS.2011.2162082 - Previsão de carga de curto prazo baseada em um modelo aditivo semiparamétrico
As Figuras 8-11 (vermelho não são dias úteis) representam esses valores defasados em relação ao consumo real de energia.
Há uma leve correlação para esses recursos gerados.
# Check Correlation
cor <- cor(cleaned_power_consum[sapply(cleaned_power_consum, is.numeric)], method = c("pearson", "kendall", "spearman"), use = "complete.obs")
| Recurso | Correlação com PowerConsum |
|---|---|
| Feriado Suavizado | -0,556194 |
| Média da última semana | 0,389044 |
| MédiaLastTwoDays | 0,201253 |
| MaxLastOneDay | 0,320193 |
| MinLastOneDay | 0,348583 |
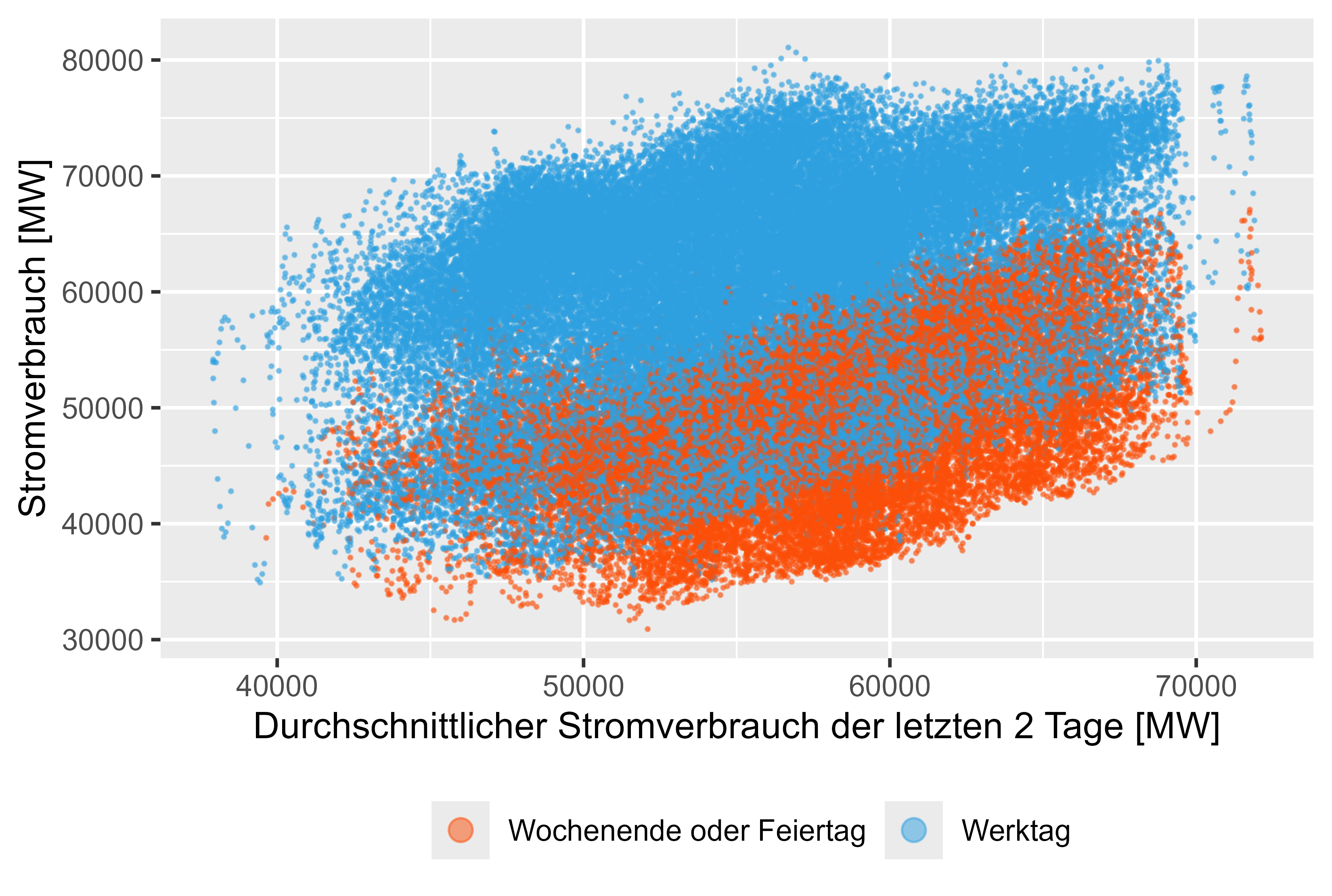Figura 8 Consumo de energia - MeanLastTwoDays
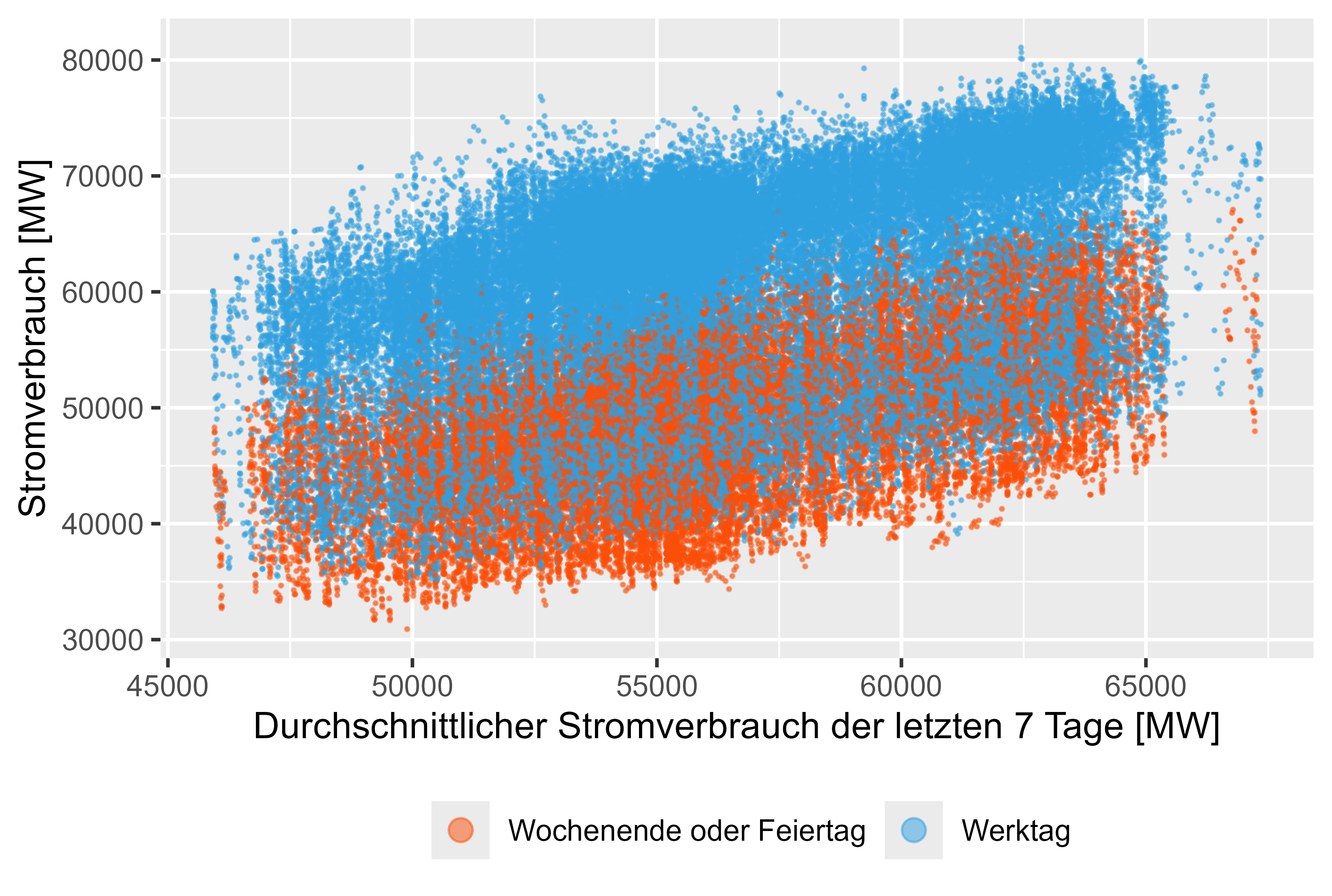Figura 9 Consumo de energia - MeanLastWeek
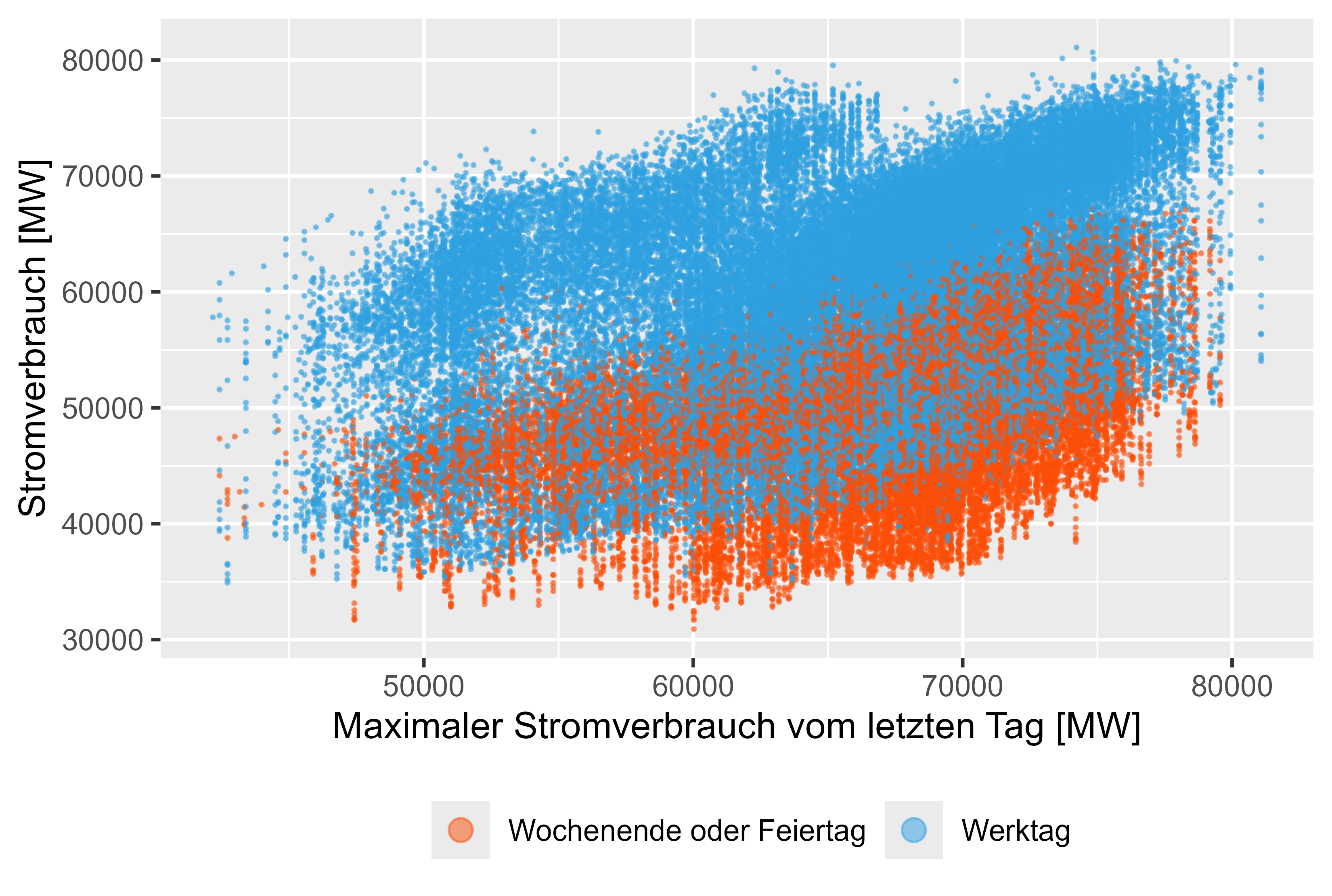Figura 10 Consumo de energia - MaxLastOneDay
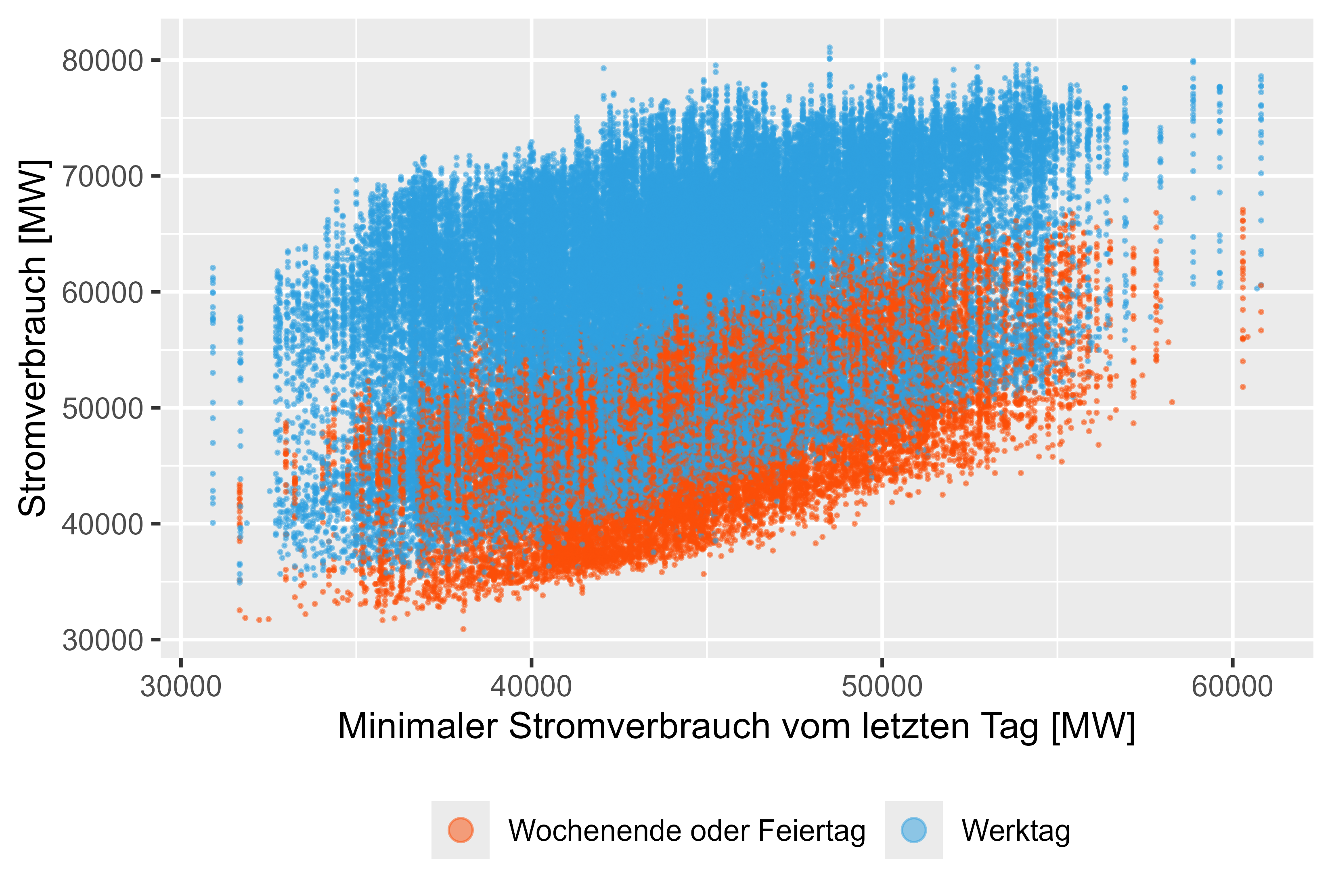Figura 11 Consumo de energia - MinLastOneDay
Existe uma sazonalidade complexa. Para a resolução horária existe uma sazonalidade anual, semanal e diária. O que precisa ser rastreado pelo modelo. A solução aqui é discutida em Previsão: Princípios e Prática, Capítulo 12.1 Sazonalidade complexa para usar termos de Fourier para representar e montar via cos() e sin() a sazonalidade complexa.
Podemos ter uma pequena visão do gráfico ACF e PACF, há poucos picos significativos, mas é apenas a representação de 96 valores defasados. Se considerarmos as ~9.000 observações defasadas de um ano, haveria uma sazonalidade complexa. É por isso que é mais fácil usar o termo de Fourier. Também não funcionou bem apenas encontrar componentes PDQ e PDQ por
ARIMA(...
stepwise=FALSE,
greedy=FALSE,
approx=FALSE)
em si. Além disso, o tempo de treinamento aumenta dramaticamente sem os termos de Fourier.
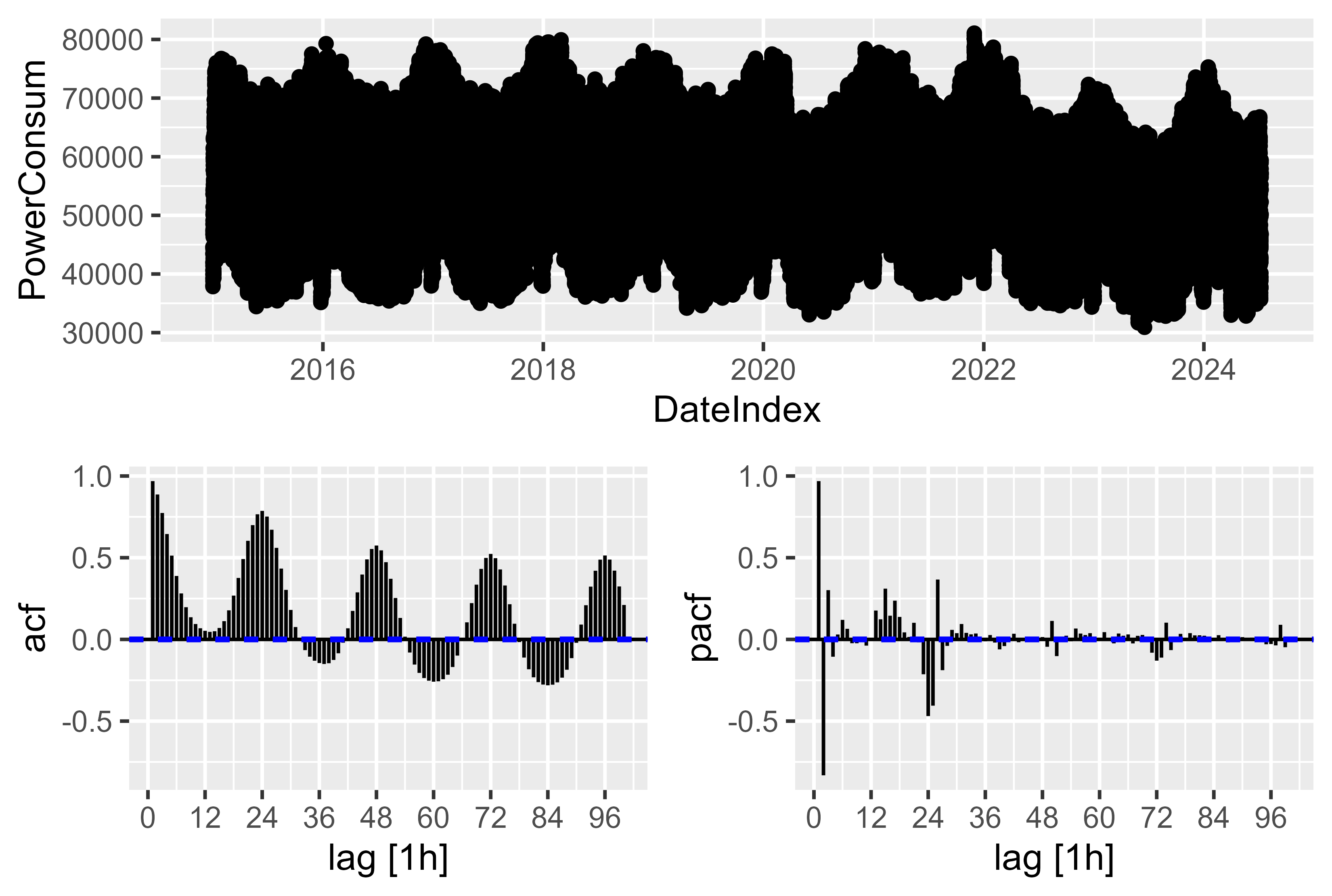Figura 12 Consumo de energia - ACF PACF Gráfico do consumo de energia bruta
A melhor combinação de recursos encontrada neste trabalho é:
Para comparar os modelos utilizamos as métricas MAE e MAPE. SMARD é o modelo de "Bundesnetzagentur" da página SMARD. O modelo do Profeta também foi testado, teve um desempenho sólido, mas não foi bom o suficiente.
Os valores previstos pela SMARD atingiram um MAPE de 3,6%. <- NÃO NESTE ESTUDO.
Dados de treinamento:
O melhor modelo encontrado até agora guerra LHM + DHR (modelo harmônico linear + regressão harmônica dinâmica)
A ideia é agrupar um modelo linear com o modelo ARIMA. Porque era difícil para o modelo ARIMA lidar com variáveis fictícias para feriados. Portanto, o modelo conjunto ajudou.
train_power_consum <- cleaned_power_consum |>
filter(year(DateIndex) > 2020 & (year(DateIndex) < 2024))
generate_models(model_name = "model/mean_naive_drift",
train_power_consum = train_power_consum)
train_power_consum_v5 <- train_power_consum |>
mutate(HolidaySmoothed = Holiday + sin(2 * pi * (as.numeric(Hour)+1) / 24))
holiday_effect_model <- lm(
PowerConsum ~
HolidaySmoothed,
data = train_power_consum_v5
)
saveRDS(holiday_effect_model, file = "ensemble_model/version_5/holiday_effect_2021_2023.rds")
train_power_consum_v5$Residuals <- residuals(holiday_effect_model)
fit <- train_power_consum_v5 |>
model(
ARIMA = ARIMA(Residuals ~
PDQ(0,0,0)
+ pdq(d=0)
+ MeanLastWeek
+ WorkDay
+ EndOfTheYear # new
+ FirstWeekOfTheYear # new
+ MeanLastTwoDays
+ MaxLastOneDay
+ MinLastOneDay
+ fourier(period = "day", K = 6)
+ fourier(period = "week", K = 7)
+ fourier(period = "year", K = 3)
)
)
saveRDS(fit, file = "ensemble_model/version_5/arima_2021_2023.rds")
Poderíamos visualizar o efeito e como o modelo funciona. A Figura 13 mostra a ideia por trás deste modelo. Primeiramente ajustamos o modelo LHM e calculamos os resíduos. Treine o modelo DHR pelos resíduos e some ambos. É uma espécie de espelho no LHM e empurra os valores de volta ao topo.
Para o modelo LHM usamos aqui uma abordagem simples, uma curva sinusal que se repete a cada 24 horas e diminui ou aumenta em feriados ou dias úteis.
Ao prever o LHM com base em novos dados, podemos prever os resíduos para novos dados. Resíduos + LHM deslocam os valores de volta para a posição “correta”.
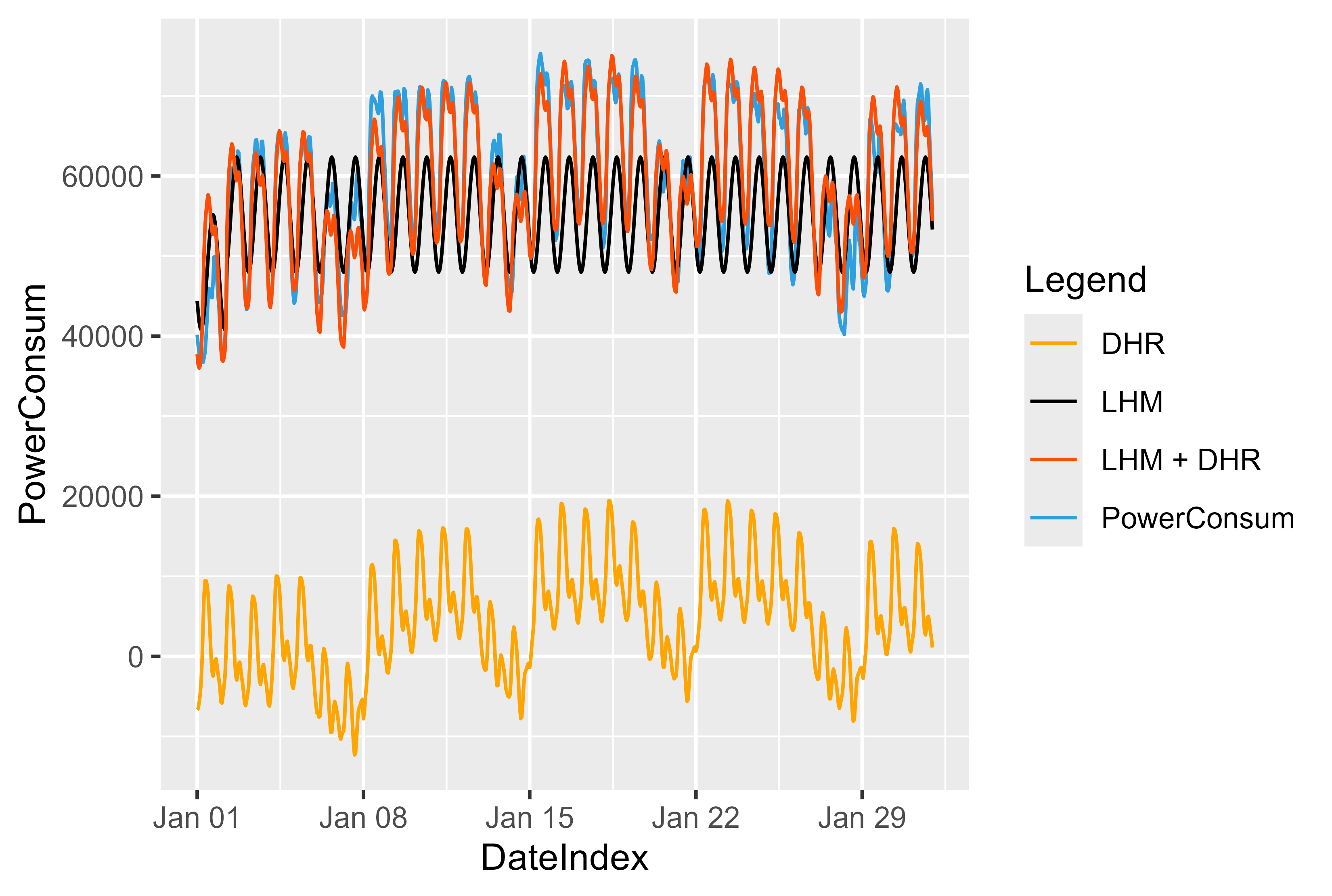Figura 13 Representação do modelo LHM + DHR
ensembled_fc <- load_ensembled_models(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
real_data = cleaned_power_consum,
smard_fc = cleaned_smard_pred,
model_path = "ensemble_model"
)
all_forecasts_ensembled <- ensembled_fc$all_forecasts
raw_fc_ensembled <- ensembled_fc$raw_forecasts
fc <- load_all_model_results(
days_to_forecast = 40,
months_to_forecast = 6,
year_to_forecast = 2024,
starting_month = 1,
smard_fc = cleaned_smard_pred,
real_data = cleaned_power_consum
)
all_forecasts <- fc$combined_forecasts
raw_fc <- fc$raw_forecasts
metric_results <- calculate_metrics(fc_data = all_forecasts, fc_data_ensembled=all_forecasts_ensembled)
# Plot best Model for single Models
name_of_best_model_for_single_model <- plot_forecast(
all_forecasts = all_forecasts,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
raw_fc = raw_fc,
month_to_plot = 1,
days_to_plot = 40
)
# Plot best Model for ensembled Models
name_of_best_model_ensembled <- plot_forecast_ensembled(
all_forecasts = all_forecasts_ensembled,
metric_results = metric_results,
cleaned_power_consum = cleaned_power_consum,
month_to_plot = 1,
days_to_plot = 40
)
# Residuals Compared with SMARD
plot_compare_with_smard(
all_forecasts = all_forecasts_ensembled,
name_of_best_model = name_of_best_model_ensembled
)
# LHM DHM representation
plot_representation_of_lhm_dhm_components(path_dhm = "ensemble_model/version_5/arima_2021_2023.rds",
path_lhm = "ensemble_model/version_5/holiday_effect_2021_2023.rds",
from_month = 1,
to_month = 1,
raw_fc_ensembled = raw_fc_ensembled)
Uma pontuação sólida de MAPE 3,8% para a versão_5 (modelo LHM + DHR).
Vamos dar uma olhada mais profunda se usarmos apenas o modelo ARIMA (arima_14). A Figura 14 representa os resultados deste modelo. Podemos ver feriados (laranja), fim de semana (vermelho) e dias normais (azul). Existem valores discrepantes significativos para os feriados, embora houvesse uma variável fictícia para o modelo ARIMA, ela não conseguiu capturar os feriados corretamente.
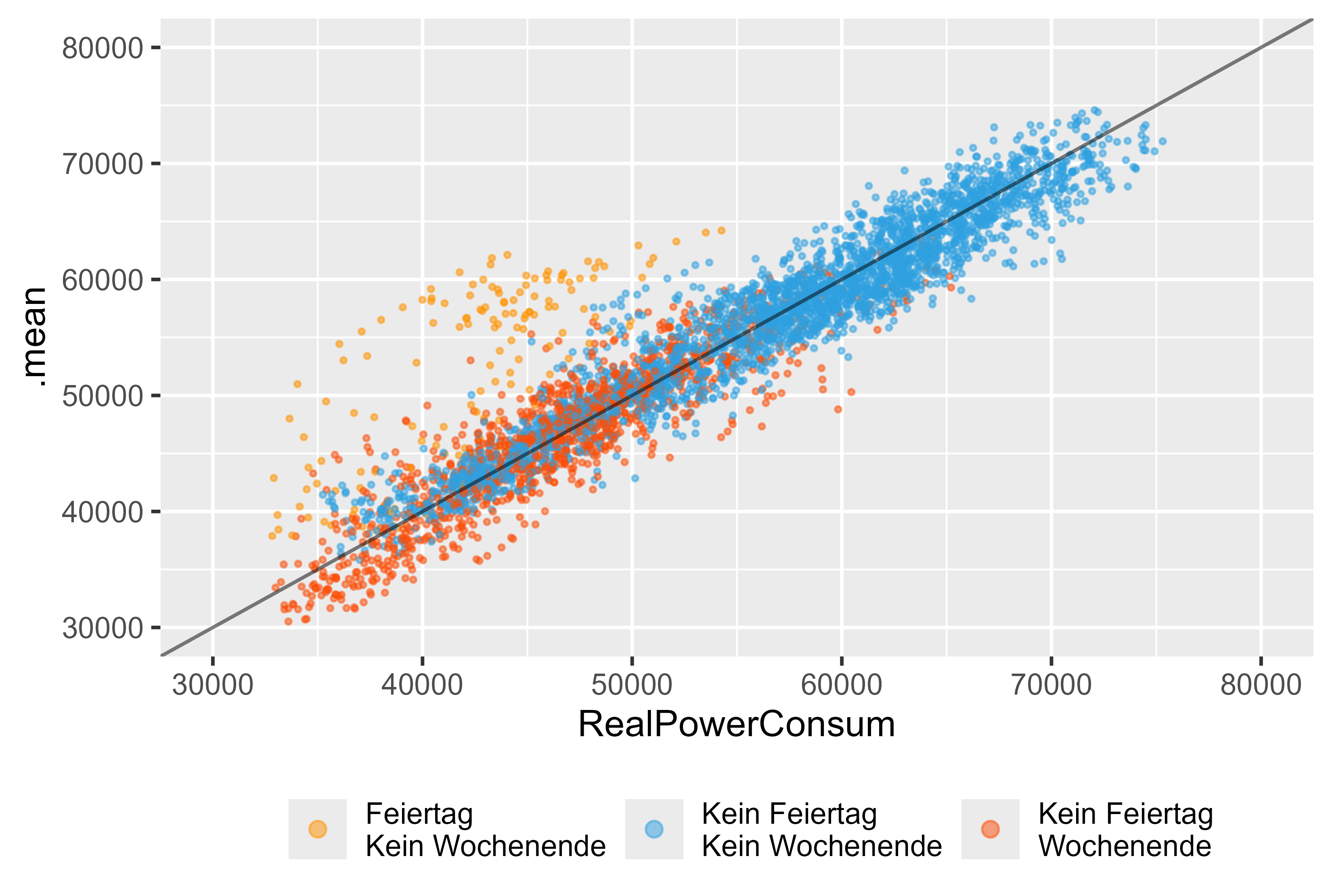Figura 14 Previsão vs Valores Reais ARIMA (DHR, arima_14), como um modelo único
Por outro lado o Modelo LHM + DHR apresenta um melhor desempenho para as férias. A Figura 15 representa isso.
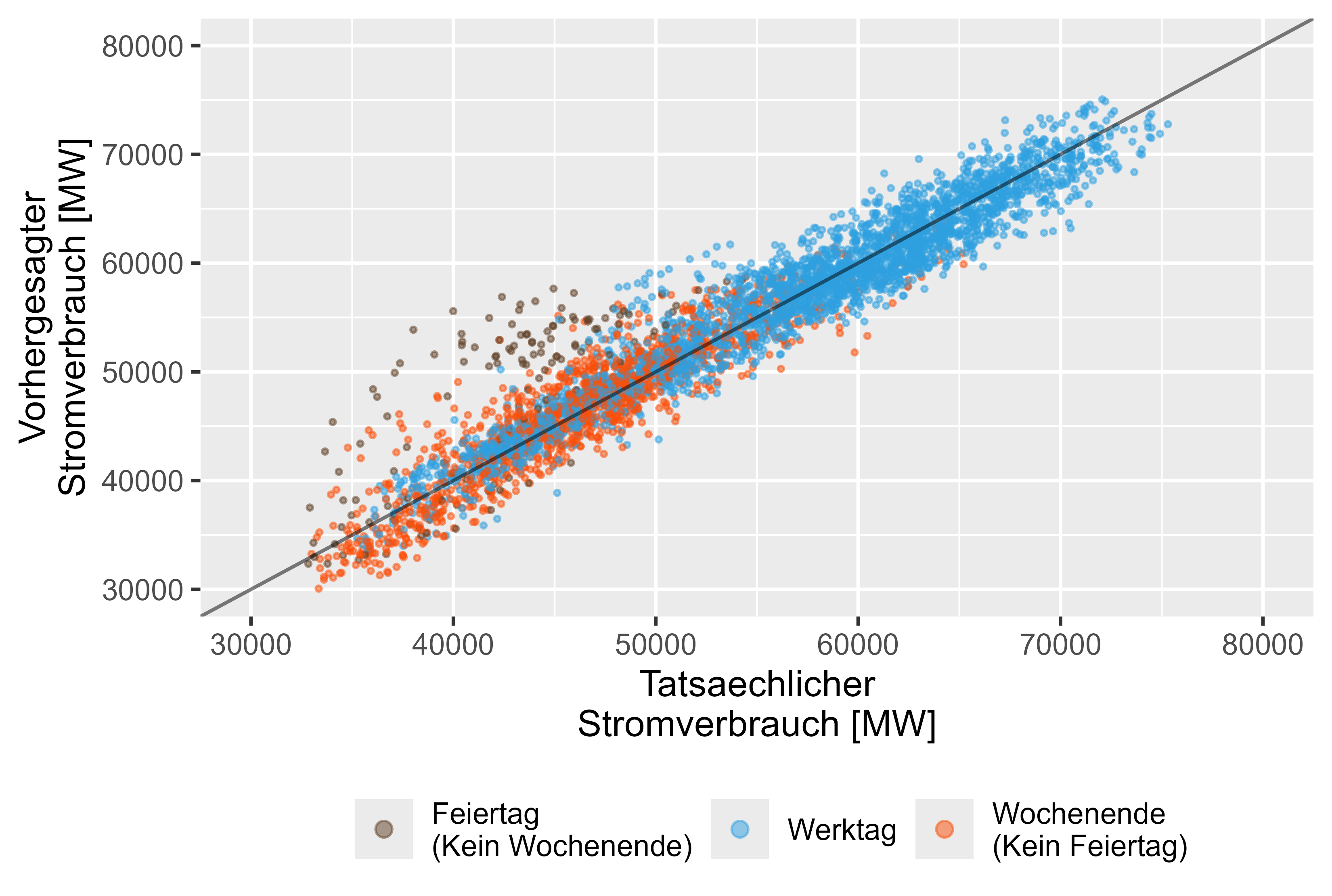Figura 15 Previsão vs Valores Reais LHM + DHR, modelo conjunto
A Figura 16 mostra a previsão para janeiro de 2024. Parece razoável.
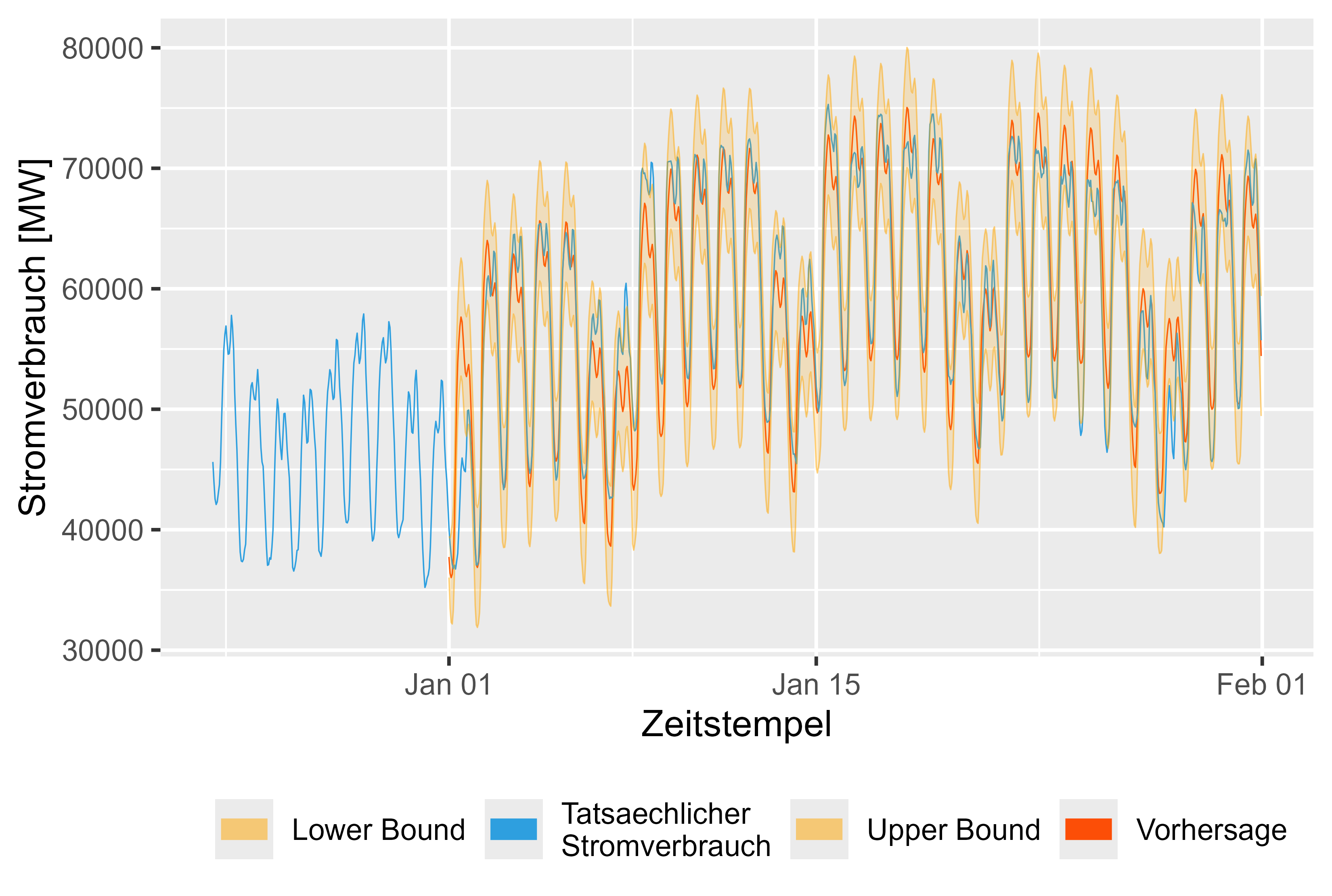Figura 16 Previsão versus valores reais LHM + DHR para janeiro de 2024
Além disso, os resíduos do modelo comparados com o modelo SMARD parecem bons. Existem poucos picos que podem ser significativos e podem ser melhor preparados por modelagem. Mas no geral um resultado sólido.
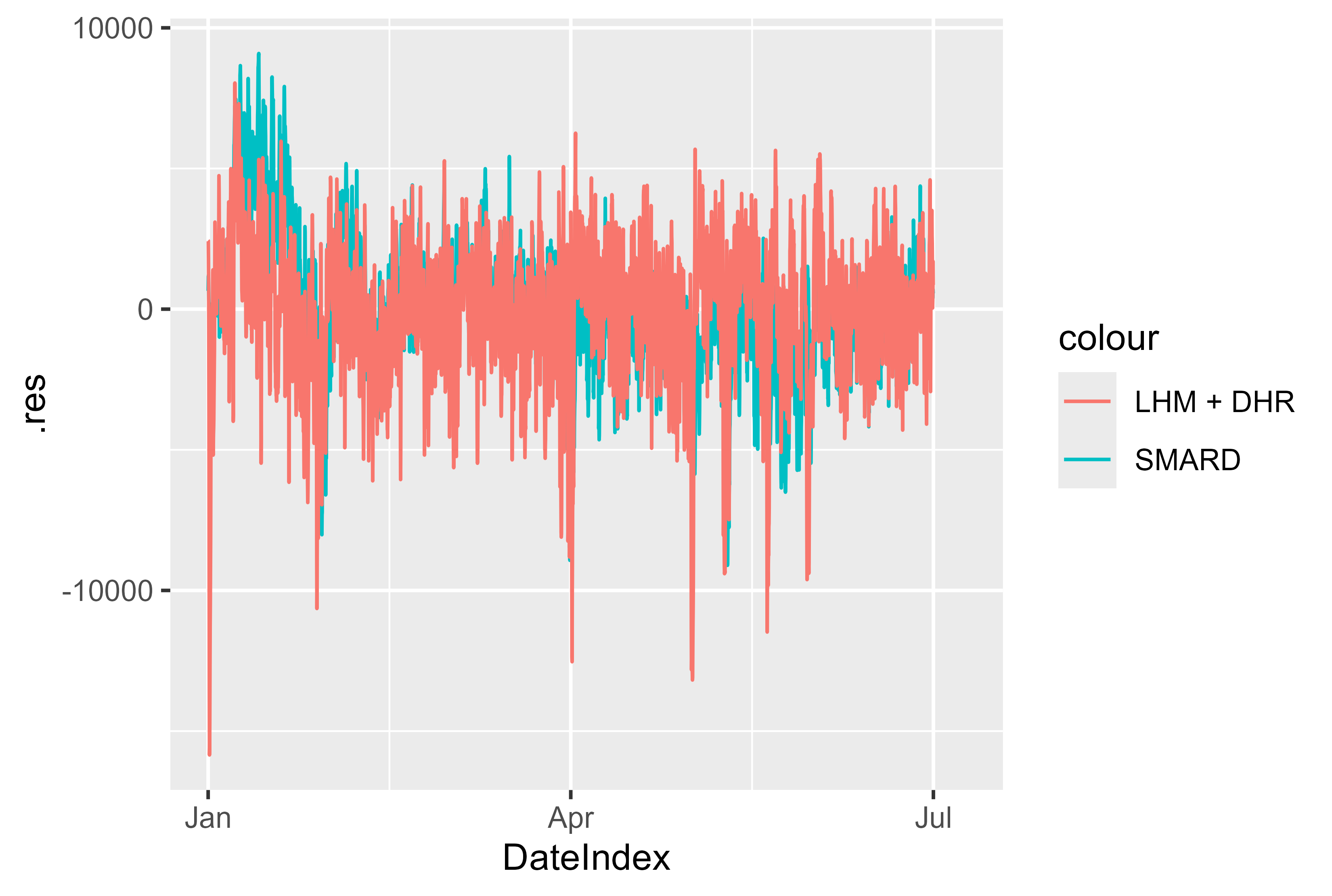Figura 17 Residuais LHM + DHR de janeiro a julho de 2024
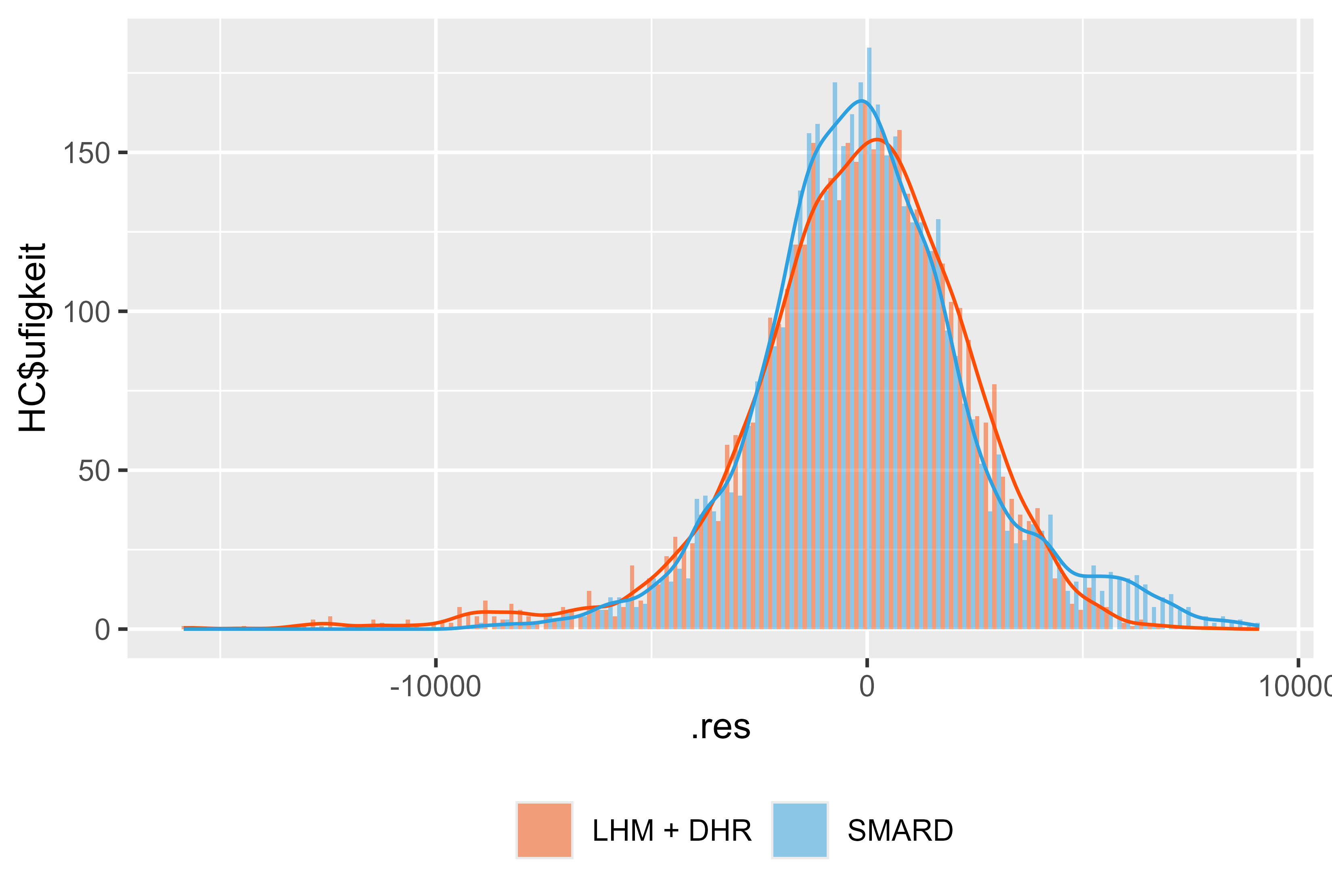Figura 18 Residuais LHM + DHR de janeiro a julho de 2024
| Índice | Nome do modelo | REQM | MAPE | MAE | Conjunto |
|---|---|---|---|---|---|
| 2 | Observações reais | 0,000 | 0,000000 | 0,000 | verdadeiro |
| 3 | SMARD | 2480.693 | 3.602140 | 1869.466 | FALSO |
| 4 | SMARD | 2480.693 | 3.602140 | 1869.466 | verdadeiro |
| 5 | versão_5 | 2626.807 | 3.816012 | 1937.670 | verdadeiro |
| 6 | versão_0 | 2613.258 | 3.846888 | 1946.314 | verdadeiro |
| 7 | versão_7 | 2770.359 | 4.107272 | 2076.045 | verdadeiro |
| 8 | versão_8 | 2775.441 | 4.146788 | 2091.153 | verdadeiro |
| 9 | versão_9 | 2887.179 | 4.177841 | 2100.381 | verdadeiro |
| 10 | versão_6 | 2906.242 | 4.216517 | 2142.092 | verdadeiro |
| 11 | arima_14_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSO |
| 12 | arima_18_2021_2023.rds | 3208.735 | 4.389492 | 2207.395 | FALSO |
| 13 | versão_4 | 2875.929 | 4.535388 | 2255.645 | verdadeiro |
| 14 | versão_2 | 2905.990 | 4.580770 | 2279.624 | verdadeiro |
| 15 | arima_9_2021_2023.rds | 3267.160 | 4.611857 | 2302.918 | FALSO |
| 16 | arima_2_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 17 | arima_4_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 18 | arima_5_2021_2023.rds | 3251.390 | 4.614028 | 2301.447 | FALSO |
| 19 | arima_13_2021_2023.rds | 3283.745 | 4.619636 | 2307.415 | FALSO |
| 20 | arima_10_2021_2023.rds | 3265.913 | 4.625508 | 2314.395 | FALSO |
| 21 | arima_0_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSO |
| 22 | arima_17_2021_2023.rds | 3269.009 | 4.645944 | 2317.138 | FALSO |
| 23 | arima_16_2021_2023.rds | 3298.902 | 4.673116 | 2334.857 | FALSO |
| 24 | arima_1_2021_2023.rds | 3312.429 | 4.696342 | 2340.193 | FALSO |
| 24 | profeta_0_2021_2023.rds | 3044.849 | 4.711527 | 2435.572 | FALSO |
| 25 | arima_8_2021_2023.rds | 3332.217 | 4.716612 | 2358.085 | FALSO |
| 26 | arima_11_2021_2023.rds | 3358.020 | 4.758970 | 2388.791 | FALSO |
| 27 | arima_12_2021_2023.rds | 3430.191 | 5.022772 | 2495.067 | FALSO |
| 28 | arima_7_2021_2023.rds | 3475.671 | 5.049287 | 2510.903 | FALSO |
| 29 | versão_3 | 3546.729 | 5.064654 | 2570.530 | verdadeiro |
| 30 | arima_15_2021_2023.rds | 3734.584 | 5.165147 | 2606.661 | FALSO |
| 31 | arima_6_2021_2023.rds | 3748.583 | 5.375326 | 2723.837 | FALSO |
| 32 | versão_1 | 4495.568 | 6.483477 | 3229.647 | verdadeiro |
| 33 | arima_3_2021_2023.rds | 4558.982 | 6.953247 | 3453.387 | FALSO |
| 34 | tslm_0_2021_2023.rds | 6760.994 | 11.189119 | 5694.949 | FALSO |
| 35 | média_2021_2023.rds | 9489.303 | 16.406032 | 8101.476 | FALSO |
| 36 | ingênuo_2021_2023.rds | 14699.338 | 20.797370 | 12130.587 | FALSO |
| 37 | drift_2021_2023.rds | 14763.692 | 20.917883 | 12200.002 | FALSO |
OBSERVAÇÃO:
Verifique exemplo/ensemble_model_2022_forecast ou exemplo/ensemble_model_2023_forecast
Poderíamos incluir mais fatores como:
