Resolve o quebra-cabeça da Torre de Hanói por meio do aprendizado por reforço.
Em um ambiente Python com Numpy e Pandas instalados, execute o script hanoi.py para produzir os três gráficos mostrados na seção Resultados. O script pode ser facilmente adaptado para jogar com um número diferente de discos N , por exemplo.
O aprendizado por reforço recebeu recentemente interesse renovado com a surra de um jogador humano profissional de Go pelo AlphaGo do Google Deepmind. Aqui, um quebra-cabeça mais simples é resolvido: o jogo Torre de Hanói. A implementação segue o algoritmo Q-learning originalmente proposto por Watkins & Dayan [1].
O jogo Torre de Hanói consiste em três pinos e vários discos de tamanhos diferentes que podem deslizar sobre os pinos. O quebra-cabeça começa com todos os discos empilhados no primeiro pino em ordem crescente, com o maior na parte inferior e o menor no topo. O objetivo do jogo é mover todos os discos para o terceiro pino. Os únicos movimentos legais são aqueles que levam o disco superior de um pino para outro, com a restrição de que um disco nunca pode ser colocado sobre um disco menor. A Figura 1 mostra a solução ideal para 4 discos.

Figura 1. Uma solução animada do quebra-cabeça da Torre de Hanói para 4 discos. (Fonte: Wikipédia).
Seguindo Anderson [2], representamos o estado do jogo por tuplas, onde o i- ésimo elemento denota em qual pino o i- ésimo disco está. Os discos são rotulados em ordem crescente de tamanho. Assim, o estado inicial é (111), e o estado final desejado é (333) (Figura 2).
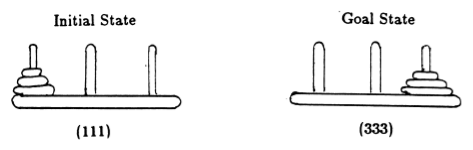
Figura 2. Estados inicial e objetivo do quebra-cabeça da Torre de Hanói com 3 discos. (De [2]).
Os estados do quebra-cabeça e as transições entre eles correspondentes aos movimentos legais formam o gráfico de transição de estado do quebra-cabeça, mostrado na Figura 3.
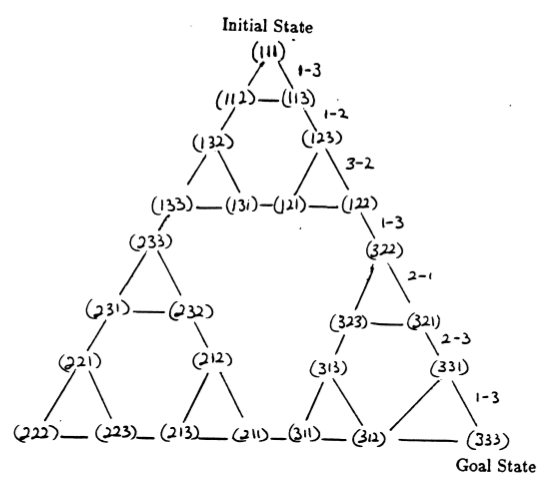
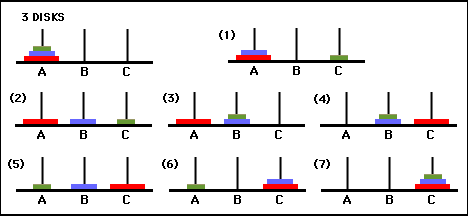
Figura 3. Gráfico de transição de estado para o quebra-cabeça de três discos da Torre de Hanói (acima) e a solução ideal de 7 movimentos correspondente (abaixo), que segue o caminho do lado direito do gráfico. (De [2] e Mathforum.org).
O número mínimo de movimentos necessários para resolver um quebra-cabeça da Torre de Hanói é 2 N - 1, onde N é o número de discos. Assim, para N = 3, o quebra-cabeça pode ser resolvido em 7 movimentos, conforme mostrado na Figura 3. Na seção seguinte, descrevemos como isso é alcançado pelo Q-learning.
R e a matriz de 'valor de ação' Q para 2 discos O primeiro passo do programa é gerar uma matriz de recompensa R que captura as regras do jogo e dá uma recompensa por vencê-lo. Para simplificar, a matriz de recompensa é mostrada para N = 2 discos na Figura 4.
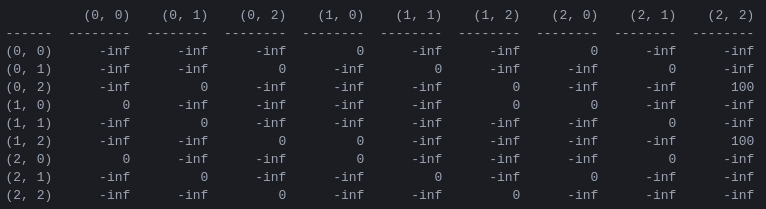
Figura 4. Matriz de recompensa R para um quebra-cabeça da Torre de Hanói com N = 2 discos. O ( i , j )-ésimo elemento representa a recompensa por passar do estado i para j . Os estados são rotulados por tuplas como nas Figuras 2 e 3, com a diferença de que os pinos são indexados 'pythonicamente' de 0 a 2 em vez de 1 a 3. Os movimentos que levam ao estado objetivo (2,2) recebem uma recompensa de 100, movimentos ilegais de e todos os outros movimentos de 0.
A matriz de recompensa R descreve apenas recompensas imediatas : uma recompensa de 100 só pode ser alcançada nos penúltimos estados (0,2) e (1,2). Nos outros estados, cada um dos 2 ou 3 movimentos possíveis tem uma recompensa igual a 0, e não há razão aparente para escolher um em vez do outro.
Em última análise, procuramos atribuir um “valor” a cada movimento possível em cada estado, de modo que, ao maximizar estes valores, possamos definir uma política que conduza à solução óptima. A matriz de 'valores' para cada ação em cada estado é chamada Q e pode ser resolvida recursivamente, ou 'aprendida', de maneira estocástica, conforme descrito por Watkins & Dayan [1]. O resultado para 2 discos é mostrado na Figura 5.
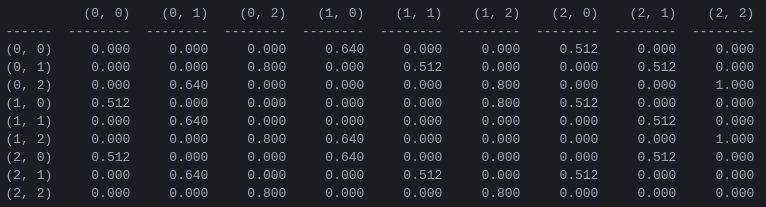
Figura 5. Matriz Q de 'valor de ação' para o jogo Torre de Hanói com 2 discos, aprendido com fator de desconto de = 0,8, fator de aprendizagem = 1,0 e 1000 episódios de treinamento.
Os valores da matriz Q são essencialmente pesos que podem ser atribuídos aos vértices do grafo de transição de estado da Figura 3, que guiam o agente do estado inicial ao estado objetivo da maneira mais curta possível. Neste exemplo, começando no estado (0,0) e escolhendo sucessivamente o movimento com maior valor de Q , o leitor pode se convencer de que a matriz Q conduz o agente pela sequência de estados (0,0) - (1 ,0) - (1,2) - (2,2), que corresponde à solução ótima de 3 movimentos do jogo Torre de Hanói de 2 discos (Figura 6).
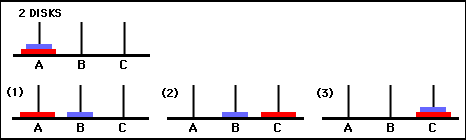
Figura 6. Solução do jogo Torre de Hanói com 2 discos. Os estados consecutivos são representados por (0,0), (1,0), (1,2) e (2,2), respectivamente. (Fonte: mathforum.org).
Neste exemplo onde a matriz Q convergiu para o seu valor óptimo, define uma política estacionária : cada linha contém uma acção com um valor máximo único. Durante o processo de aprendizagem, entretanto, ações diferentes podem ter o mesmo valor de Q . (Em particular, este é o caso no início do treinamento, quando Q é inicializado em uma matriz de zeros). Nas simulações apresentadas na seção seguinte, tais situações são tratadas pela seguinte política estocástica : nos casos em que o valor máximo de Q é compartilhado entre diversas ações, escolha aleatoriamente uma dessas ações.
O desempenho do algoritmo Q-learning pode ser medido contando o número de movimentos necessários (em média) para resolver o quebra-cabeça da Torre de Hanói. Este número diminui com o número de episódios de treinamento até atingir o valor ideal 2 N - 1, onde N é o número de discos, conforme ilustrado na Figura 7 para N = 2, 3 e 4.
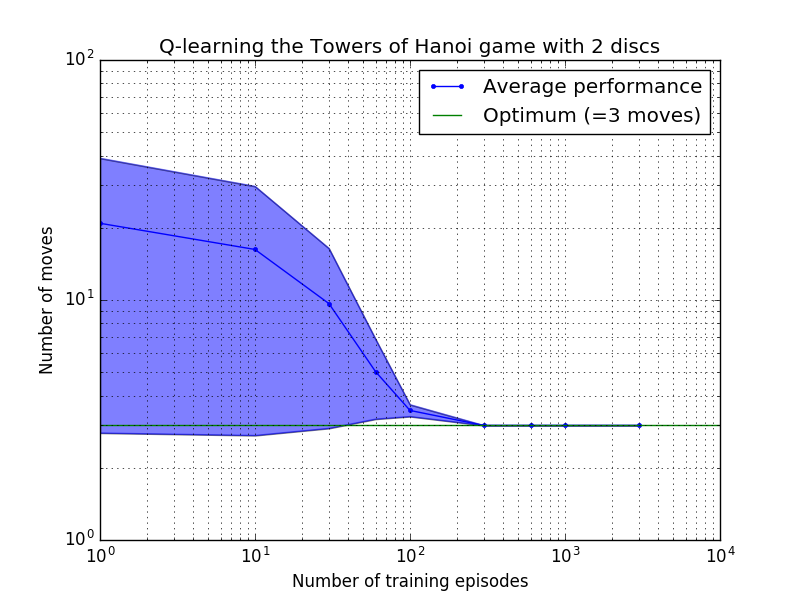
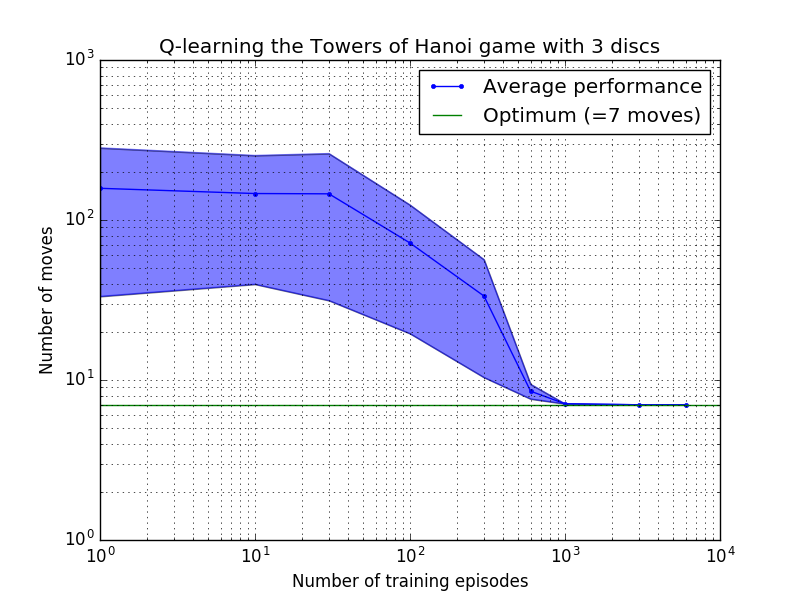
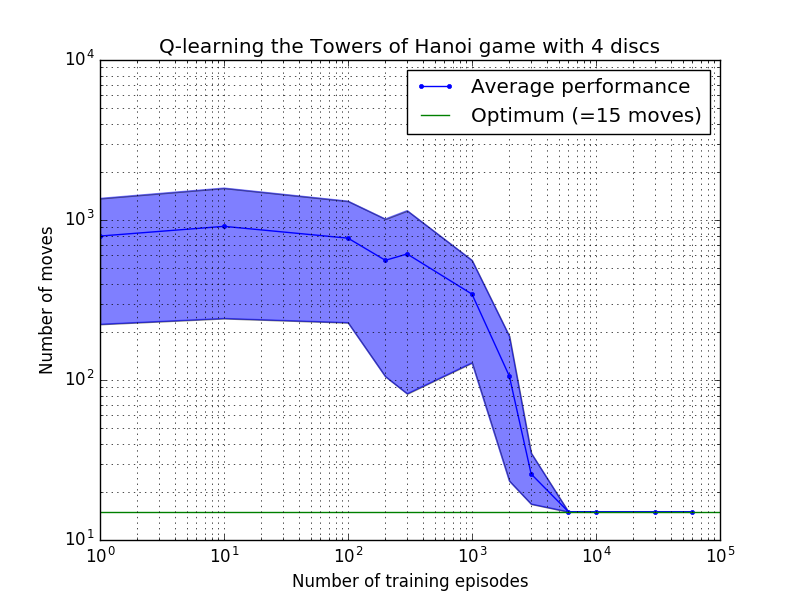
Figura 7. Desempenho do algoritmo Q-learning para o jogo Torre de Hanói com, de cima para baixo, 2, 3 e 4 discos. Em todos os casos a aprendizagem foi realizada com fator de desconto = 0,8 e fator de aprendizagem = 1,0. A curva azul sólida representa o desempenho médio em 100 épocas de treinamento e jogo 100 vezes para cada política estocástica resultante. Os limites superior e inferior da área sombreada em azul são compensados da média pelo desvio padrão estimado. (Para N = 3 e N = 4, o número de episódios de treinamento e os tempos de jogo foram reduzidos para 10 e 10, respectivamente, devido a restrições computacionais).
Uma característica interessante das características de aprendizagem na Figura 7 é que em todos os casos, a aprendizagem é inicialmente lenta, e o agente dificilmente se sai melhor do que a política de “treinamento zero” de escolha de movimentos aleatoriamente. Em algum momento, a aprendizagem atinge um “ponto de inflexão” e depois converge para o número ideal de movimentos a um ritmo acelerado (embora isto seja um pouco exagerado pela escala logarítmica).
Um script Python resolve com sucesso o quebra-cabeça da Torre de Hanói de maneira ideal para qualquer número de discos por meio de Q-learning. O script pode ser facilmente adaptado a outros problemas com uma matriz de recompensa R diferente.
O número de episódios de treinamento necessários para convergir para uma solução ótima aumenta muito com o número de discos N : para N=2 discos são necessários ~300 episódios, enquanto para N=4 são necessários ~6.000. Uma possível melhoria do algoritmo de aprendizagem seria permitir que ele buscasse automaticamente soluções recursivas, como feito por Hengst [3].
[1] Watkins & Dayan, Q-learning , Machine Learning, 8, 279-292 (1992). (PDF).
[2] Anderson, Aprendizagem e resolução de problemas com sistemas conexionistas multicamadas , Ph.D. tese (1986). (PDF).
[3] Hengst, Discovering Hierarchy in Reinforcement Learning with HEXQ , Anais da Décima Nona Conferência Internacional sobre Aprendizado de Máquina (2002). (PDF).