O Risk é um jogo de tabuleiro estratégico de diplomacia, conflito e conquista para dois a seis jogadores. Vire gira entre os jogadores que controlam exércitos de tocar peças com as quais tentam capturar territórios de outros jogadores, com resultados determinados por rolos de dados. O objetivo do jogo é ocupar todos os territórios do conselho e, ao fazê -lo, eliminar os outros jogadores. Cada turno consiste em duas ações:
O objetivo deste projeto foi implementar o jogo de risco com algumas mudanças feitas nas regras e projetar um agente artificialmente inteligente, capaz de jogar o jogo corretamente e ter uma chance muito alta de ganhar ao enfrentar outros oponentes, incluindo os dois humanos reais jogadores ou outros jogadores de agentes.
O jogo é implementado usando a linguagem de programação Java. Controlando turnos, executando ações solicitadas, atualizando o mapa do jogo, verificando se tudo está acontecendo de acordo com as regras, etc., são as coisas que essa parte do código faz. A interface do usuário do jogo também foi projetada através de arquivos .fxml que desenham o mapa e é a plataforma que conecta o player à lógica do jogo.
Esta seção se concentra na implementação e avaliação das heurísticas que levam a uma forte IA para o risco de jogo.
A implementação é baseada no algoritmo de poda alfa-beta minimax. O jogador constrói uma árvore de previsão baseada no algoritmo DFS.
Sempre que é a vez do agente jogar, uma árvore é feita. Os nós da árvore são os estados do jogo (mapa do jogo nesse estado) e cada borda é um possível ataque feito do estado atual ao estado de resultado do ataque do mapa. Uma ação de ataque consiste nas coordenadas dos territórios de início e alvo e o número de unidades escolhidas para estar no exército atacante. O nó raiz é o estado atual do mapa de onde um jogador precisa escolher seus movimentos. Embora a árvore não possa prever até o estado final do jogo devido ao grande número de movimentos possíveis que um jogador pode ter em cada estado que a memória e os limites de tempo não permitem. Portanto, o jogador só pode construir a árvore com uma certa profundidade que definimos no código. Existem também algumas simplificações aplicadas a partes específicas da estratégia de jogos do agente que serão explicadas nas seções a seguir. Para tomar a melhor decisão possível, as heurísticas de decisão são definidas para os nós mais profundos possíveis (folhas de árvores) que avaliam quanto alcançar esse estado pode ser benéfico para o jogador. Disse que as heurísticas serão explicadas ainda mais no relatório. Quando os valores das folhas forem determinados, a árvore será passada para a poda alfa-beta minimax e esse algoritmo bem conhecido encontrará a melhor série de ações que o jogador pode ter.
O fornecimento de unidades aos territórios pode ser uma tarefa complicada; No sentido de que queremos melhorar nosso poder de ataque, mas também certifique -se de ter um poder de defesa suficiente em territórios que correm o risco de serem atacados. A implantação de unidades em países adjacentes aos territórios inimigos pode ser uma maneira inteligente de manter o equilíbrio entre esses dois objetivos.
Draft simplificação:
A previsão e a inclusão de todos os cenários de rascunho possíveis na árvore de previsão levará a uma árvore complexa que enfrentaria os problemas mencionados antes; Portanto, uma das simplificações feitas é que usamos uma heurística de redação, que provou sempre ter o melhor resultado possível e prever que os oponentes também fazem essa abordagem na redação; Em outras palavras, removemos os resultados da redação como possibilidades formam a árvore de previsão e as alteramos para cenários definitivos de rascunho.
Para fazer isso, tomamos as seguintes medidas:
Draft Heuristic:
Etapa 1:
Aking the Somation de todas as unidades nos países inimigos, adjacente ao país X dará uma medida que chamamos de ameaça à segurança da fronteira (BST) em x.
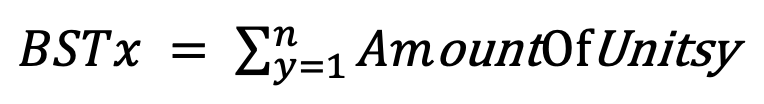
Etapa 2:
A divisão deste BST pelas unidades situadas em X fornece uma taxa de segurança de fronteira (BSR), que pode ser comparada entre todos os países de fronteira.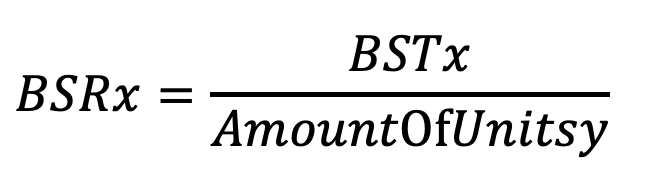
Os países com uma BSR alta têm maior probabilidade de serem conquistados por um jogador inimigo, uma vez que o número de unidades inimigas em países inimigos adjacentes é relativamente maior que o número de unidades no próprio país. A escolha de países com uma alta BSR para fornecer aumentará sua força defensiva, diminuindo a BSR. O fornecimento de unidades aos países com uma BSR mais baixa, o que significa que eles já têm uma melhor postura defensiva, aumentará sua força ofensiva, aumentando as chances de um ataque bem -sucedido desses países.
Etapa 3:
A normalização do BSR dividindo -o pela soma de todos os BSRs de países, um jogador, possui, dará uma medição direta pela qual alguém poderia organizar unidades. A taxa de segurança de fronteira normalizada (NBSR) é calculada por: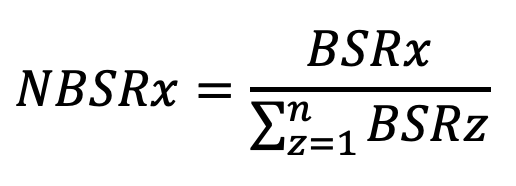
Dá uma proporção direta de como as unidades podem ser distribuídas entre os países. Nesse ponto, podemos ver que haveria um problema com esses índices porque alguns dados são irrelevantes e não queremos adicionar unidades a todos os nossos territórios, por isso definimos um limiar entre as etapas dois e três, classificando os dados do BSRX em em Uma ordem decrescente (estamos nos concentrando mais em fortalecer o poder de defesa), divida os dados do meio e defina os números na metade inferior a zero.
Etapa 4: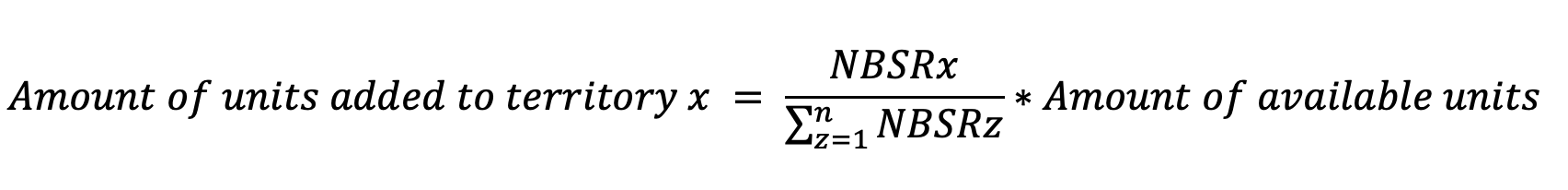
A etapa 4 será continuada até que não sejam deixadas mais unidades disponíveis para adicionar.
Existem algumas simplificações aplicadas na fase de ataque para tornar a árvore menos complicada para que possamos prever níveis mais profundos dela. Isso pode ser feito verificando quais cenários de ataque têm uma chance maior de vencer a batalha e apenas incluí -los na árvore.
Para avaliar o quão benéfico é uma folha de árvore para esse jogador específico; Definimos quatro características heurísticas que seus melhores pesos possíveis são encontrados durante o aprendizado da heurística que será explicada mais tarde. Todos os recursos retornam um resultado entre zero a um, porque quando os recursos são avaliados em índices próximos, o aprendizado e a atribuição de peso seriam mais precisos.
Os recursos são:
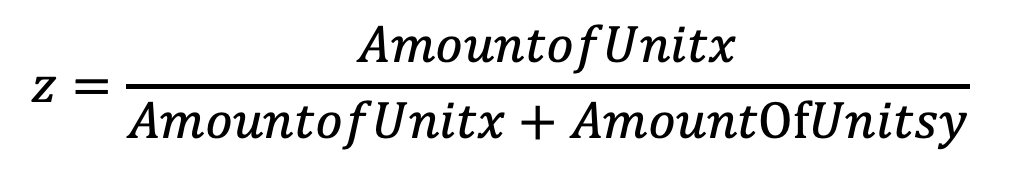
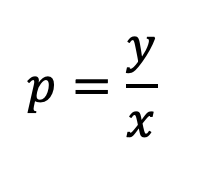
Dar peso a cada uma das heurísticas na parte anterior ajuda a avaliar o quão importante e influente cada um deles é para um agente vencer o jogo. O processo de encontrar esses pesos é através de genéticos e aprender. Cada gene é um conjunto de quatro pesos para esses quatro recursos. Começamos gerando 100 conjuntos de pesos aleatórios na faixa [0,10]. Depois disso, 10 torneios acontecerão. Para cada torneio, 10 genes da população primária serão selecionados aleatoriamente. Todos os pares possíveis de genes serem jogados um contra o outro e o resultado de cada jogo em cada torneio serão documentados. A função de fitness é definida como (número de vitórias / número de jogos) para cada gene. Os três genes principais em cada torneio (com base na função de condicionamento físico) serão selecionados, então agora temos 30 genes principais selecionados. Entre eles, selecionamos 12 pares aleatórios e, para cada par, realizam um crossover que está criando um novo gene calculando o peso médio do par de genes. Portanto, agora temos 12 novos genes deste crossover. Por outro lado, 3 genes são selecionados aleatoriamente dentro dos 30 genes que tivemos e mudam -os alterando um peso aleatório de um para outro peso aleatório no alcance [0,10]. Depois de tudo isso, agora temos 15 genes novos que são colocados na população primária, substituindo os 15 menos bons que já tínhamos lá. Neste ponto, a segunda geração de genes é gerada. Esse processo continuará a se repetir até que a geração 4 dos genes sejam gerados. O gene superior nessa população será selecionado como nossos melhores pesos para as características de nossa heurística que o agente usará para jogar.