
e as tarefas do Fiber no React, e diferentes tarefas do Fiber têm prioridades diferentes para processar tarefas com alta prioridade primeiro. Por exemplo, os cliques e entradas do usuário são tarefas de alta prioridade, porque as operações do usuário definitivamente esperam ter efeitos imediatos, de modo a melhorar a experiência do usuário. Por exemplo, a prioridade dos eventos de animação deve ser menor. Depois que uma nova tarefa de alta prioridade entra na fila, o React precisa processá-la primeiro.
Para armazenar essas tarefas, existem dois pools de tarefas no React.
//As tarefas são armazenadas em um heap mínimo var taskQueue = []; var timerQueue = [];
taskQueue e timerQueue são ambos arrays. O primeiro armazena tarefas a serem executadas imediatamente, enquanto o último armazena tarefas que podem ser atrasadas.
var novaTask = {
id: taskIdCounter++, // Marca o id da tarefa
callback, // função de retorno de chamada prioridadeLevel, // prioridade da tarefa startTime, // hora de início da tarefa, ponto no tempo expirationTime, // tempo de expiração, ponto no tempo sortIndex: -1, // classificação da tarefa, o valor vem do tempo de expiração, então o valor Quanto menor o valor, maior a prioridade}; Assim que uma nova tarefa chegar no React, ele primeiro usará currentTime para registrar a hora atual (performance.now() ou Date.now()). parâmetro de atraso, então a tarefa inicia o tempo de execução startTime = currentTime + delay;. A seguir, se startTime > currentTime for estabelecido, isso prova que a tarefa pode ser adiada, então a tarefa entra no timerQueue, caso contrário, entra no taskQueue.
Como o React encontra a tarefa com a prioridade mais alta? Tome taskQueue como exemplo. É um pool de tarefas dinâmico (fila de tarefas) e o formulário de dados é um array. Claro, você pode classificar de acordo com a prioridade, ou seja, Array.sort Quando uma nova tarefa é adicionada à fila, ela é classificada primeiro e, em seguida, a tarefa com maior prioridade é encontrada e executada. Mas a complexidade média de tempo de Array.sort é O(nlogn), o que não é a melhor solução.
SortIndex é usado para classificação em newTask do taskQueue. Este valor é retirado do tempo de expiração, o que significa que quanto maior a prioridade da tarefa, mais ela precisa ser compreendida e executada, portanto o tempo de expiração será menor. maior a prioridade, o tempo de expiração. Quanto menor o tempo, menor será naturalmente o sortIndex. Na verdade, esta é uma fila prioritária .
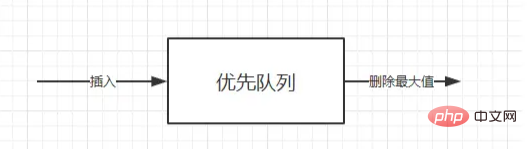
A fila de prioridade também é um tipo de fila ( em primeiro lugar, é uma fila e, em segundo lugar, tail in, first out ). A única diferença é que a ordem de desenfileiramento da fila de prioridade é baseada na prioridade em alguns casos; , pode ser necessário encontrar O elemento mínimo ou máximo no conjunto de elementos pode ser operado usando a fila de prioridade ADT. A fila de prioridade ADT é uma estrutura de dados que suporta a inserção e exclusão de operações de valor mínimo (retornando e excluindo o elemento mínimo) ou. excluindo a operação de valor máximo (retornando e excluindo o elemento mínimo, remova o maior elemento).
Se o elemento com o menor valor de chave tiver a prioridade mais alta, essa fila de prioridade será chamada de fila de prioridade ascendente (ou seja, o menor elemento será sempre excluído primeiro). Da mesma forma, se o elemento com o maior valor de chave tiver a prioridade mais alta, então esse tipo de fila de prioridade é chamada de fila de prioridade descendente (ou seja, o maior elemento é sempre excluído primeiro, pois esses dois tipos são simétricos, você só precisa); para focar em um deles, como fila de prioridade ascendente.
Por exemplo : quando estávamos comprando ingressos, estávamos todos na fila e tínhamos a mesma prioridade. Quem estava na frente da fila compraria o ingresso primeiro. Mas aí veio um soldado e ele tinha prioridade maior e estava direto na fila. . A frente.
O heap mínimo (heap raiz pequeno, heap superior pequeno...) é usado no React para atingir esta função. Isso é transformar o taskQueue em um heap mínimo e, em seguida, retirar a tarefa principal para execução, empilhar o taskQueue e mantê-lo como uma estrutura de dados de heap mínimo. Ao inserir uma nova tarefa no taskQueue, ela também deve ser amontoada e sempre mantida como heap mínimo.
: Em alguns lugares, o heap é chamado de fila de prioridade (não é preciso, em primeiro lugar, é uma fila e tem as características de uma fila, ou seja, " primeiro a entrar, primeiro a sair "). . Em segundo lugar, os elementos desta fila têm prioridades e aqueles com prioridades mais elevadas serão classificados em primeiro lugar.
Para ser mais preciso, um heap é uma forma de implementar uma fila de prioridade. É claro que as filas prioritárias também podem ser implementadas de outras maneiras.
Dissemos antes que a classificação de heap é uma classificação instável, mas taskQueue espera que esse processo seja estável. Ou seja, se for possível que o tempo de expiração de duas tarefas seja o mesmo, então depende de quem entra. primeiro, o pool de tarefas é o valor do id de newTask. Cada vez que uma nova tarefa chega, o id será aumentado em 1.
função comparar(a, b) {
// Compare primeiro o índice de classificação e depois o ID da tarefa.
const diff = a.sortIndex - b.sortIndex;
retornar diferença! == 0? diferença: a.id - b.id;
} Antes de entender o heap mínimo, vamos revisar o conhecimento básico.
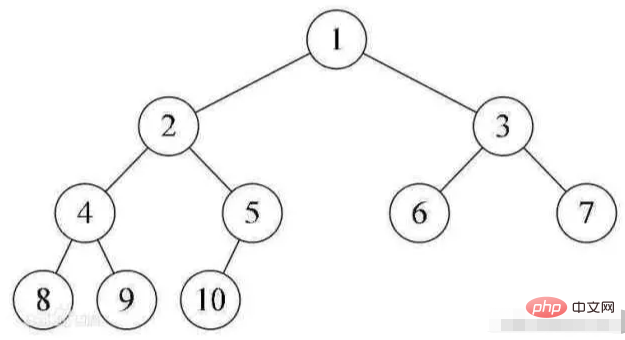
refere-se a uma árvore ordenada em que o grau dos nós da árvore não é superior a 2. É a árvore mais simples e importante.
é uma árvore binária na qual todos os nós em cada nível possuem dois nós filhos, exceto o último nível que não possui nenhum nó filho.
Do ponto de vista gráfico, uma árvore binária completa se parece com um triângulo.
Se o número de níveis de uma árvore binária for K e o número total de nós for (2^k) -1, então é uma árvore binária completa.
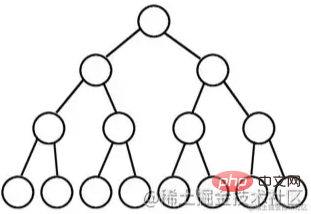
Uma árvore binária completa significa “filhas têm ambos os lados” e é muito perfeita, por isso é chamada de árvore binária completa.
excluindo os nós folhas, o grau de todos os nós é 2. Em outras palavras, o grau de todos os nós só pode ser 0 ou 2.
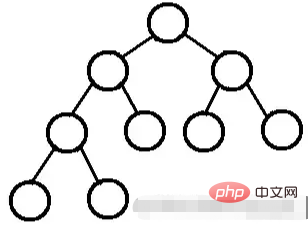
Uma árvore binária perfeita não tem filhos ou tem ambos os filhos.
O texto original em inglês de Árvore Binária Completa:
Uma árvore binária completa (FBT) é uma árvore na qual cada nó, exceto as folhas, tem dois filhos.
O texto original em inglês da árvore binária perfeita:
Uma árvore binária perfeita (PBT) é uma árvore com todos os nós de folhas na mesma profundidade. Todos os nós internos têm grau 2.
Todos os livros estrangeiros referem-se aos primeiros livros traduzidos sobre árvores binárias completas e árvores binárias perfeitas, mas os primeiros artigos traduzidos são traduzidos incorretamente. Agora, na China, só podemos cometer erros quando eles estão errados (todos estão errados, então o errado também está certo. Por exemplo, os lobistas...). Se você quiser discutir esses dois conceitos com amigos estrangeiros, preste atenção.
Uma árvore binária(CBT) é uma árvore binária na qual cada nível, exceto possivelmente o último, é completamente preenchido e todos os nós estão o mais à esquerda possível.
Uma árvore binária com n nós de profundidade k , numera os nós no. árvore de cima para baixo e da esquerda para a direita. Se o nó numerado i (1≤i≤n) estiver na árvore binária com o nó numerado i na árvore binária completa, se as posições forem iguais, a árvore binária será. chamada de árvore binária completa.
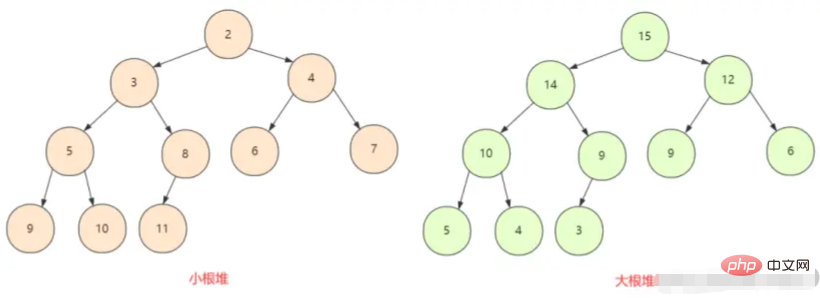
O heap sempre satisfaz as seguintes propriedades:
devemos primeiro entender o grande heap raiz
;o heap raiz pequeno Em uma árvore binária completa Todos os nós são maiores (ou menores) que seus nós filhos, portanto, há duas situações aqui, o heap máximo e o heap mínimo.
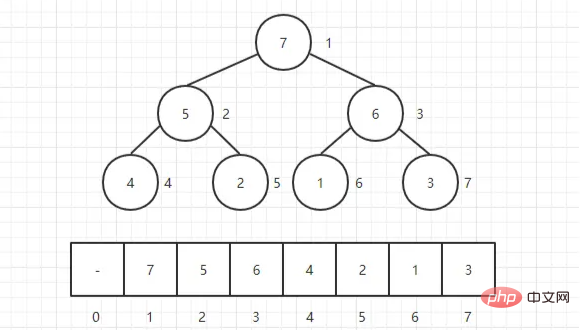
O heap geralmente é um array de objetos que pode ser visto como uma árvore binária completa . É claro que as árvores binárias também podem ser representadas por arrays.
é construir o heap primeiro e depois ajustá-lo.
, para uma árvore binária (representação de array), ajustamos de baixo para cima, começando no "primeiro nó não folha" e ajustando para frente. As regras de ajuste são as seguintes:
Construir um heap é O(n). ) processo de complexidade de tempo.
① Comece a partir do primeiro nó não folha para julgar a troca para baixo (shiftDown), para que o nó atual e o filho possam manter as propriedades do heap
. ② No entanto, a substituição comum do nó pode não ser um problema se a troca quebrar as propriedades da estrutura do heap. do filho, então ele deve ser re-ShiftDown no nó trocado até parar.
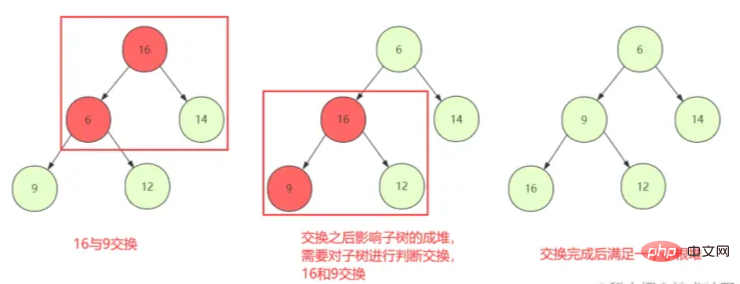
a estrutura do heap
destruir a estrutura da pilha.
① Então simplesmente coloque o último elemento primeiro. Desta forma, você só precisa julgar o deslocamento de troca (shiftDown), mas precisa observar que o tamanho de todo o heap mudou neste momento. Não usaremos logicamente a posição descartada, então precisamos incluir um heap. parâmetro de tamanho ao projetar a função.
② Repita a operação acima até que todos os elementos da pilha sejam obtidos.
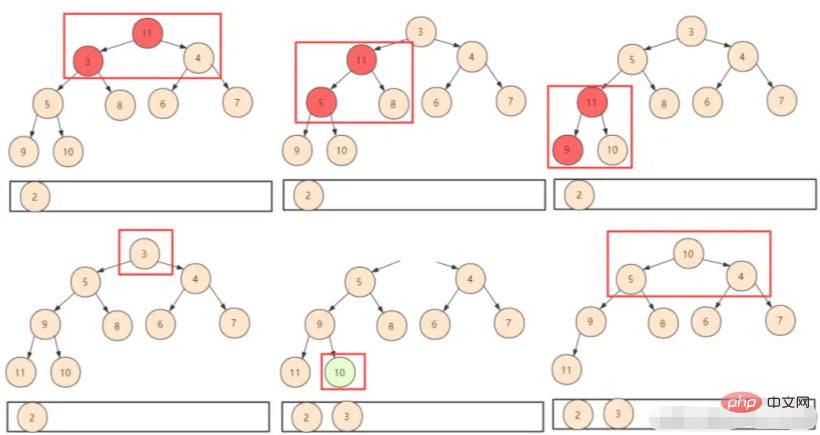
Em termos de análise da complexidade do algoritmo de heap, a complexidade do tempo de construção do heap anterior era O(n). Cada vez que o topo do heap é excluído e depois trocado para baixo, o número de cada um é logn. Desta forma, a complexidade é O(nlogn) e a complexidade total do tempo é O(n)+O(nlogn)=O(nlogn).
Heap é adequado para manter o valor máximo da coleção.
Depois que um elemento é retirado do heap, o custo de reajuste para obter o elemento superior do heap (ou seja, o segundo valor mais alto) é relativamente baixo, porque depois que o elemento é retirado, o heap é um semi -produto acabado, e o segundo valor mais alto é obtido de um produto semiacabado. É claro que o custo é relativamente baixo e a complexidade do tempo é O (logn), mas se for percorrido uma vez para encontrar o segundo valor mais alto, a complexidade do tempo é O (n).
código de implementação do código é escrito em Javascript ES6.
classeHeap {
construtor(dados, comp) {
estes.dados = dados? dados: [];
// Regras de comparação: mais flexíveis, você pode comparar valores ou objetos this.compartor = comp ? comp : (ab) => ab;
// Ajusta para heap (fila de prioridade)
this.heapify();
}
heapify() {
if(this.size() <= 1) retornar;
// Comece a ajustar a partir do primeiro nó não folha ou você pode ajustar a partir do último elemento for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Ajuste o heap. O ajuste para baixo também pode ser implementado usando recursão. Aqui, a iteração é usada para implementar this.shiftDown(i);
}
}
// Ajusta para baixo shiftDown(i) {
deixe para a esquerda = 2*i +1;
deixe para a direita = 2*i +2;
deixe len = this.size();
while(i <len) {
deixe findIndex = i;
//O filho da esquerda é "maior"
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
encontrarIndex = esquerda;
}
// O filho certo é "maior"
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
encontrarIndex = certo;
}
if(i! == encontrarIndex) {
//Troca o nó atual por um valor maior [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// Após ajustar esta camada, isso pode afetar as características do heap da camada inferior, então continue ajustando a camada inferior (implementação iterativa ou recursiva)
i = encontrarIndex;
esquerda = 2*i +1;
direita = 2*i +2;
}
outro {
// Se nenhum ajuste for necessário, salte (deve saltar, caso contrário o loop não poderá terminar)
quebrar;
}
}
}
// Ajusta para cima shiftUp(i){
// Encontre o subscrito do pai let parentIndex = Math.floor((i-1)/2);
//Ajusta o máximo para 0
while(parentIndex >=0 ) {
deixe findIndex = i;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = parentIndex;
}
if(encontrarÍndice! == i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
i = encontrarIndex;
parentIndex = Math.floor((i-1)/2);
}
outro {
quebrar;
}
}
}
// Obtém o número de todos os elementos no heap size(){
retorne este.data.length;
}
// Obtém o primeiro elemento do heap peek(){
if(!this.size()) retorna nulo;
retorne isto.dados[0];
}
//Adiciona um elemento ao heap push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Extrai o primeiro elemento do heap pop(){
if(!this.size()) retorna nulo;
deixe res = this.data[0];
if(este.tamanho() == 1) {
this.data.pop();
}
outro {
estes.dados[0] = estes.dados[este.dados.comprimento-1];
este.dados.comprimento = este.dados.comprimento-1;
this.shiftDown(0);
}
retornar res;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
deixe comp = (a, b) => ab;
deixe heap = novo Heap (arr, comp);
deixe res = [];
enquanto(heap.size()) {
res.push(heap.pop());
}
console.log(res); O elemento em arr também pode ser um objeto.
O diretório packages/scheduler no código-fonte do React é o código relacionado ao módulo de agendamento de tarefas do React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Copyright (c) Facebook, Inc. e suas afiliadas.
*
* Este código-fonte está licenciado sob a licença MIT encontrada no
* Arquivo LICENSE no diretório raiz desta árvore de origem.
*
* @flow estrito
*/
digite Heap = Array<Nó>;
tipo Nó = {|
ID: número,
sortIndex: número,
|};
função de exportação push (heap: Heap, nó: Nó): void {
índice const = heap.length;
heap.push(nó);
siftUp(heap, nó, índice);
}
espiada da função de exportação (heap: Heap): Nó |
const primeiro = heap[0];
retornar primeiro === indefinido null: primeiro;
}
função de exportação pop (heap: Heap): Nó |
const primeiro = heap[0];
if (primeiro! == indefinido) {
const último = heap.pop();
if (último! == primeiro) {
pilha[0] = último;
siftDown(pilha, último, 0);
}
retorne primeiro;
} outro {
retornar nulo;
}
}
function siftUp(heap, nó, i) {
deixe índice = i;
enquanto (verdadeiro) {
const parentIndex = (índice - 1) >>> 1;
const pai = heap[parentIndex];
if (pai! == indefinido && comparar (pai, nó) > 0) {
// O pai é maior.
heap[parentIndex] = nó;
heap[índice] = pai;
índice = índicepai;
} outro {
// O pai é menor.
retornar;
}
}
}
function siftDown(heap, nó, i) {
deixe índice = i;
comprimento const = heap.length;
while (índice < comprimento) {
const leftIndex = (índice + 1) * 2 - 1;
const esquerda = heap[leftIndex];
const índicedireito = índiceesquerdo + 1;
const direita = heap[rightIndex];
// Se o nó esquerdo ou direito for menor, troque pelo menor deles.
if (esquerda!== indefinido && compare(esquerda, nó) <0) {
if (direita! == indefinido && compare (direita, esquerda) <0) {
pilha[índice] = direita;
heap[rightIndex] = nó;
índice = índicedireito;
} outro {
pilha[índice] = esquerda;
heap[leftIndex] = nó;
índice = índiceesquerdo;
}
} else if (right !== indefinido && compare(right, node) < 0) {
pilha[índice] = direita;
heap[rightIndex] = nó;
índice = índicedireito;
} outro {
// Nenhum dos filhos é menor.
retornar;
}
}
}
função comparar(a, b) {
// Compare primeiro o índice de classificação e depois o ID da tarefa.
const diff = a.sortIndex - b.sortIndex;
retornar diferença! == 0? diferença: a.id - b.id;
} O heap mínimo que implementamos é um pouco diferente da implementação no React, mas a ideia é a mesma, apenas o código é escrito de forma diferente.
o agendamento de tarefas no React é implementado usando o heap mínimo. Se tivermos um certo entendimento do heap mínimo antes, aprenderemos esse conteúdo mais rapidamente. Pessoalmente, acho que é importante acumular conhecimento desde o início, mas esse processo pode ser enfadonho. No momento, você acha que conhece alguns algoritmos? Na verdade, esses algoritmos são básicos e você ainda nem começou? Porque no cenário de agendamento de tarefas do React, os requisitos a serem implementados são muito claros, e as estruturas de dados e algoritmos a serem utilizados também são claros. Em alguns cenários reais, conhecemos os requisitos específicos, mas não sabemos quais resultados de dados e algoritmos usar. Precisamos abstrair os requisitos e projetar estruturas de dados e algoritmos específicos com base no modelo de dados abstrato. .