Решает головоломку Ханойской башни с помощью обучения с подкреплением.
В среде Python с установленными Numpy и Pandas запустите сценарий hanoi.py , чтобы создать три графика, показанные в разделе «Результаты». Скрипт можно легко адаптировать для игры, например, с другим количеством дисков N
Недавно интерес к обучению с подкреплением возобновился после победы над профессиональным игроком в го с помощью AlphaGo от Google Deepmind. Здесь решается более простая головоломка: игра «Ханойская башня». Реализация соответствует алгоритму Q-обучения, первоначально предложенному Уоткинсом и Даяном [1].
Игра «Ханойская башня» состоит из трех колышков и нескольких дисков разного размера, которые могут скользить по колышкам. Головоломка начинается с того, что все диски складываются на первый колышек в порядке возрастания: самый большой внизу, а самый маленький вверху. Цель игры — переместить все диски на третий колышек. Единственными допустимыми ходами являются те, которые переносят самый верхний диск с одной привязки на другую, с тем ограничением, что диск никогда не может быть помещен на меньший диск. На рисунке 1 показано оптимальное решение для 4 дисков.

Рисунок 1. Анимированное решение головоломки «Ханойская башня» на 4 диска. (Источник: Википедия).
Следуя Андерсону [2], мы представляем состояние игры кортежами, где i- й элемент обозначает, на какой привязке находится i -й диск. Диски маркированы в порядке возрастания размера. Таким образом, начальное состояние — (111), а желаемое конечное состояние — (333) (рис. 2).
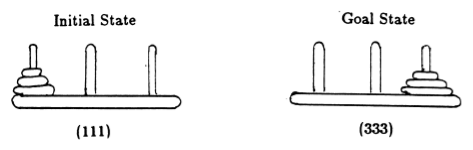
Рисунок 2. Начальное и конечное состояния головоломки «Ханойская башня» с тремя дисками. (Из [2]).
Состояния головоломки и переходы между ними, соответствующие допустимым ходам, образуют граф переходов состояний головоломки, который показан на рисунке 3.
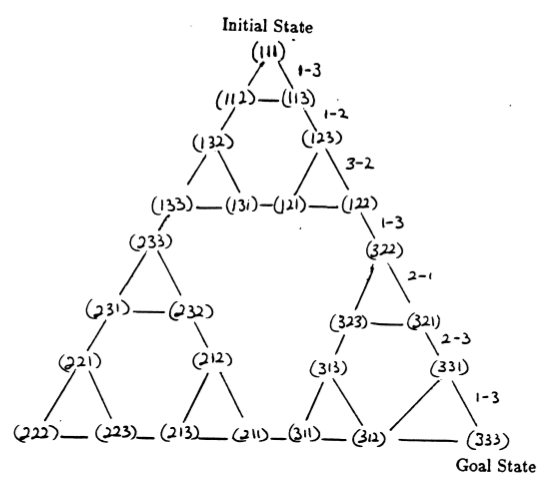
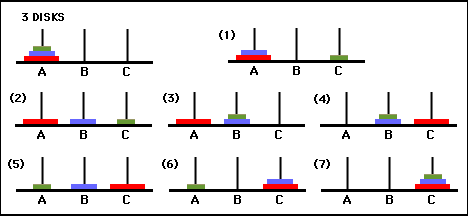
Рисунок 3. Граф переходов состояний для трехдисковой головоломки Ханойской башни (вверху) и соответствующее оптимальное решение с 7 ходами (внизу), которое следует по пути правой части графа. (Из [2] и Mathforum.org).
Минимальное количество ходов, необходимое для решения головоломки «Ханойская башня», составляет 2 N — 1, где N — количество дисков. Таким образом, при N = 3 головоломку можно решить за 7 ходов, как показано на рисунке 3. В следующем разделе мы расскажем, как это достигается с помощью Q-обучения.
R и матрица «ценности действия» Q для двух дисков. Первым шагом в программе является создание матрицы вознаграждений R , которая фиксирует правила игры и дает вознаграждение за победу в ней. Для простоты матрица вознаграждений показана для N = 2 дисков на рисунке 4.
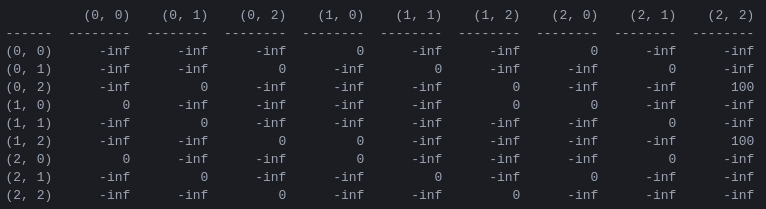
Рисунок 4. Матрица наград R для головоломки «Ханойская башня» с N = 2 дисками. ( i , j )-й элемент представляет награду за переход из состояния i в j . Состояния помечены кортежами, как на рисунках 2 и 3, с той разницей, что привязки индексируются «питонически» от 0 до 2, а не от 1 до 3. Ходам, которые приводят к целевому состоянию (2,2), назначается награда. 100, недопустимые ходы , и все остальные ходы 0.
Матрица вознаграждения R описывает только немедленные вознаграждения: вознаграждение, равное 100, может быть достигнуто только из предпоследних состояний (0,2) и (1,2). В других состояниях каждый из 2 или 3 возможных ходов имеет равную награду 0, и нет очевидной причины выбирать один из них.
В конечном счете, мы стремимся присвоить «ценность» каждому возможному ходу в каждом состоянии, чтобы, максимизируя эти значения, мы могли определить политику, ведущую к оптимальному решению. Матрица «значений» для каждого действия в каждом состоянии называется Q и может быть рекурсивно решена или «обучена» стохастическим способом, как описано Уоткинсом и Даяном [1]. Результат для двух дисков показан на рисунке 5.
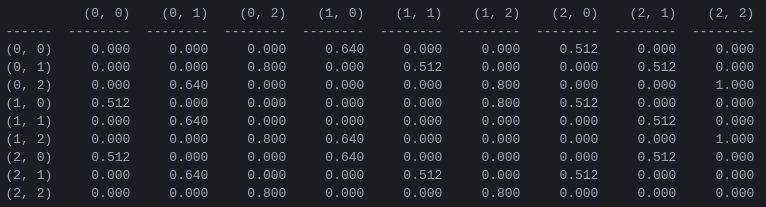
Рисунок 5. Матрица Q «Ценность действия» для игры «Ханойская башня» с двумя дисками, обученная с коэффициентом дисконтирования = 0,8, коэффициентом обучения = 1,0 и 1000 обучающими эпизодами.
Значения матрицы Q , по сути, представляют собой веса, которые можно присвоить вершинам графа перехода состояний на рисунке 3, которые кратчайшим путем ведут агента от начального состояния к целевому состоянию. В этом примере, начиная с состояния (0,0) и последовательно выбирая ход с наибольшим значением Q , читатель может убедиться, что матрица Q ведет агента через последовательность состояний (0,0) – (1 ,0) - (1,2) - (2,2), что соответствует трехходовому оптимальному решению двухдисковой игры «Ханойская башня» (рис. 6).
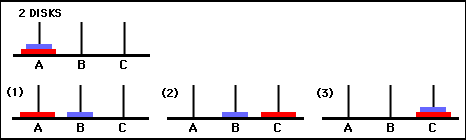
Рисунок 6. Решение игры «Ханойская башня» с двумя дисками. Последовательные состояния представлены (0,0), (1,0), (1,2) и (2,2) соответственно. (Источник: mathforum.org).
В этом примере, когда матрица Q достигла своего оптимального значения, она определяет стационарную политику: каждая строка содержит одно действие с уникальным максимальным значением. Однако в процессе обучения разные действия могут иметь одно и то же значение Q (В частности, это имеет место в начале обучения, когда Q инициализируется матрицей нулей). В моделированиях, представленных в следующем разделе, такие ситуации рассматриваются с помощью следующей стохастической политики: в случаях, когда максимальное значение Q распределяется между несколькими действиями, выберите одно из этих действий случайным образом.
Производительность алгоритма Q-обучения можно измерить, подсчитав количество ходов, необходимых (в среднем) для решения головоломки Ханойской башни. Это число уменьшается с количеством тренировочных эпизодов, пока в конечном итоге не достигнет оптимального значения 2 N - 1, где N — количество дисков, как показано на рисунке 7 для N = 2, 3 и 4.
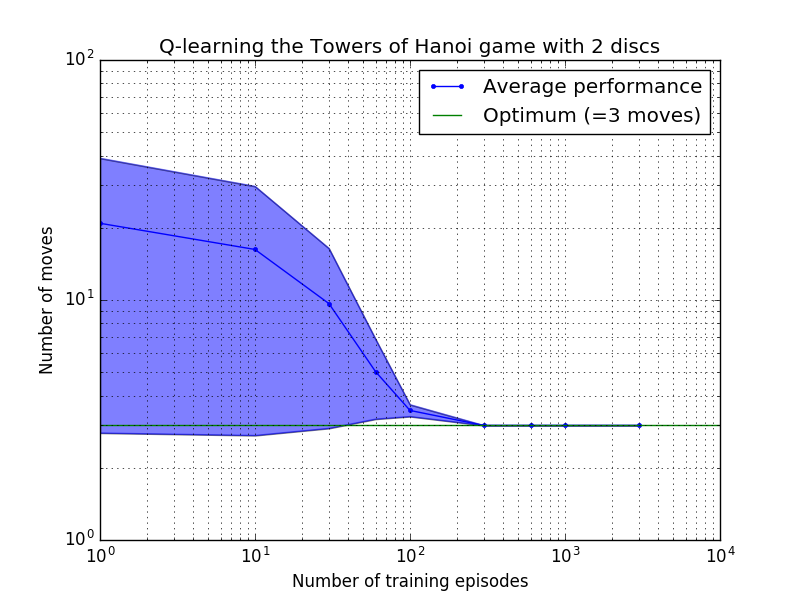
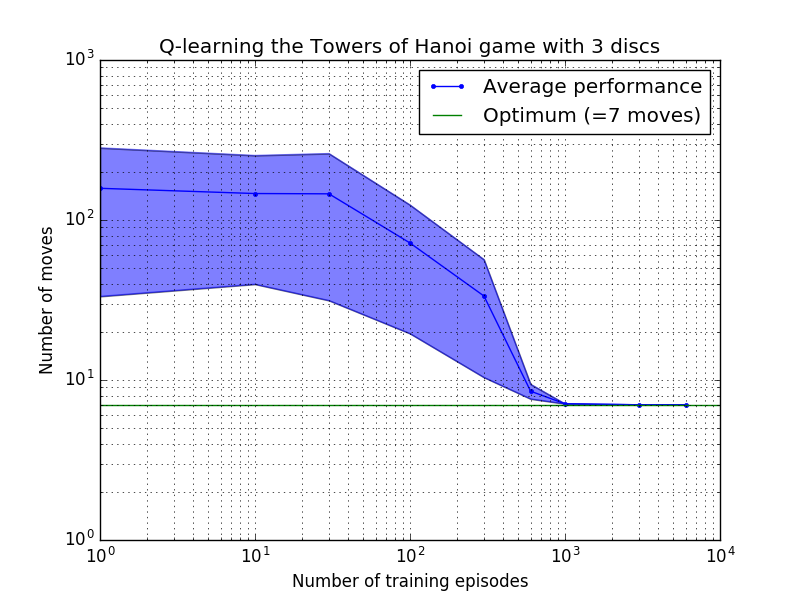
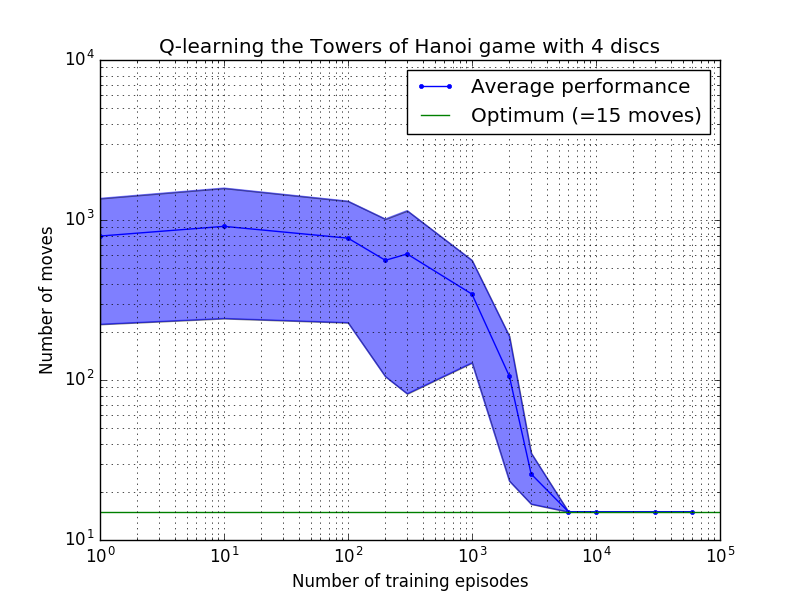
Рисунок 7. Производительность алгоритма Q-обучения для игры «Ханойская башня» с двумя, сверху вниз, 2, 3 и 4 дисками. Во всех случаях обучение проводилось с коэффициентом дисконтирования = 0,8 и коэффициентом обучения = 1,0. Сплошная синяя кривая представляет среднюю производительность за 100 периодов обучения и 100 игр в игре для каждой полученной стохастической политики. Верхняя и нижняя границы заштрихованной синей области смещены от среднего значения на расчетное стандартное отклонение. (Для N = 3 и N = 4 количество обучающих эпизодов и время игры были сокращены до 10 и 10 соответственно из-за вычислительных ограничений).
Интересная особенность характеристик обучения на рисунке 7 заключается в том, что во всех случаях обучение изначально происходит медленно, и агент едва ли добивается лучших результатов, чем политика «нулевого обучения», выбирающая ходы наугад. В какой-то момент обучение достигает «точки перегиба», а затем в ускоренном темпе сходится к оптимальному количеству ходов (хотя это несколько преувеличено в логарифмическом масштабе).
Сценарий Python успешно решает головоломку Ханойской башни оптимально для любого количества дисков с помощью Q-обучения. Сценарий можно легко адаптировать к другим задачам с другой матрицей вознаграждения R
Количество обучающих эпизодов, необходимых для сходимости к оптимальному решению, сильно возрастает с увеличением количества дисков N : для N=2 дисков требуется ~300 эпизодов, тогда как для N=4 — ~6000. Возможным улучшением алгоритма обучения могло бы стать разрешение ему автоматически искать рекурсивные решения, как это сделал Хенгст [3].
[1] Уоткинс и Даян, Q-learning , Machine Learning, 8, 279-292 (1992). (PDF).
[2] Андерсон, Обучение и решение проблем с помощью многоуровневых коннекционистских систем , доктор философии. диссертация (1986). (PDF).
[3] Хенгст, Обнаружение иерархии в обучении с подкреплением с помощью HEXQ , Материалы девятнадцатой Международной конференции по машинному обучению (2002). (PDF).