7 простых функций JavaScript, которые дадут вам представление о том, как машины на самом деле могут «обучаться».
На других языках: Русский, Португальский
Вас также может заинтересовать? Интерактивные эксперименты по машинному обучению
NanoNeuron — это упрощенная версия концепции Neuron от Neural Networks. NanoNeuron обучен преобразовывать значения температуры из Цельсия в Фаренгейт.
Пример кода NanoNeuron.js содержит 7 простых функций JavaScript (которые затрагивают прогнозирование модели, расчет стоимости, прямое/обратное распространение и обучение), которые дадут вам представление о том, как машины на самом деле могут «обучаться». Никаких сторонних библиотек, никаких внешних наборов данных или зависимостей, только чистые и простые функции JavaScript.
☝?Эти функции ни в коем случае НЕ являются полным руководством по машинному обучению. Многие концепции машинного обучения пропущены и упрощены! Это упрощение сделано специально, чтобы дать читателю действительно базовое понимание и ощущение того, как машины могут учиться, и, в конечном итоге, дать читателю возможность осознать, что это не «МАГИЯ машинного обучения», а скорее «МАТЕМАТИЧЕСКОЕ обучение машинного обучения»?
Вы, наверное, слышали о нейронах в контексте нейронных сетей. NanoNeuron — это именно то, что проще, и мы собираемся реализовать его с нуля. Для простоты мы даже не собираемся строить сеть на нанонейронах. Все это будет работать само по себе, делая для нас какие-то волшебные предсказания. А именно, мы научим этот уникальный нанонейрон преобразовывать (предсказывать) температуру от Цельсия до Фаренгейта.
Кстати, формула перевода Цельсия в Фаренгейт такова:
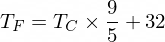
Но пока наш НаноНейрон об этом не знает...
Давайте реализуем нашу модельную функцию NanoNeuron. Он реализует базовую линейную зависимость между x и y , которая выглядит как y = w * x + b . Проще говоря, наш нанонейрон — это «ребенок» в «школе», которого учат рисовать прямую линию в координатах XY .
Переменные w , b являются параметрами модели. NanoNeuron знает только об этих двух параметрах линейной функции. Эти параметры — это то, что NanoNeuron собирается «изучить» в процессе обучения.
Единственное, что умеет NanoNeuron — это имитировать линейную зависимость. В своем методе predict() он принимает некоторые входные данные x и прогнозирует выходные данные y . Никакой магии здесь нет.
function NanoNeuron ( w , b ) {
this . w = w ;
this . b = b ;
this . predict = ( x ) => {
return x * this . w + this . b ;
}
}(...подожди... линейная регрессия, ты ли это?) ?
Значение температуры в градусах Цельсия можно преобразовать в градусы Фаренгейта по следующей формуле: f = 1.8 * c + 32 , где c — температура в градусах Цельсия, а f — расчетная температура в градусах Фаренгейта.
function celsiusToFahrenheit ( c ) {
const w = 1.8 ;
const b = 32 ;
const f = c * w + b ;
return f ;
} ; В конечном итоге мы хотим научить наш нанонейрон имитировать эту функцию (узнать, что w = 1.8 и b = 32 ), не зная этих параметров заранее.
Вот как выглядит функция преобразования Цельсия в Фаренгейт:
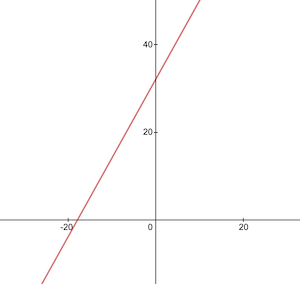
Перед обучением нам необходимо сгенерировать обучающие и тестовые наборы данных на основе функции celsiusToFahrenheit() . Наборы данных состоят из пар входных значений и правильно помеченных выходных значений.
В реальной жизни в большинстве случаев эти данные будут собираться, а не генерироваться. Например, у нас может быть набор изображений чисел, нарисованных от руки, и соответствующий набор чисел, который объясняет, какое число написано на каждом рисунке.
Мы будем использовать данные примера TRAINING для обучения нашего нанонейрона. Прежде чем наш нанонейрон вырастет и сможет самостоятельно принимать решения, нам нужно научить его, что правильно, а что нет, на обучающих примерах.
Мы будем использовать примеры TEST, чтобы оценить, насколько хорошо наш нанонейрон работает с данными, которые он не видел во время обучения. Это тот момент, когда мы увидели, что наш «ребенок» вырос и может принимать решения самостоятельно.
function generateDataSets ( ) {
// xTrain -> [0, 1, 2, ...],
// yTrain -> [32, 33.8, 35.6, ...]
const xTrain = [ ] ;
const yTrain = [ ] ;
for ( let x = 0 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTrain . push ( x ) ;
yTrain . push ( y ) ;
}
// xTest -> [0.5, 1.5, 2.5, ...]
// yTest -> [32.9, 34.7, 36.5, ...]
const xTest = [ ] ;
const yTest = [ ] ;
// By starting from 0.5 and using the same step of 1 as we have used for training set
// we make sure that test set has different data comparing to training set.
for ( let x = 0.5 ; x < 100 ; x += 1 ) {
const y = celsiusToFahrenheit ( x ) ;
xTest . push ( x ) ;
yTest . push ( y ) ;
}
return [ xTrain , yTrain , xTest , yTest ] ;
} Нам нужна какая-то метрика, которая покажет нам, насколько близок прогноз нашей модели к правильным значениям. Расчет стоимости (ошибки) между правильным выходным значением y и prediction , созданным нашим нанонейроном, будет производиться по следующей формуле:
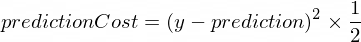
Это простая разница между двумя значениями. Чем ближе значения друг к другу, тем меньше разница. Мы используем здесь степень 2 , чтобы избавиться от отрицательных чисел, чтобы (1 - 2) ^ 2 было то же самое, что (2 - 1) ^ 2 . Деление на 2 происходит просто для дальнейшего упрощения формулы обратного распространения (см. ниже).
Функция стоимости в этом случае будет такой простой:
function predictionCost ( y , prediction ) {
return ( y - prediction ) ** 2 / 2 ; // i.e. -> 235.6
} Выполнить прямое распространение означает сделать прогноз для всех примеров обучения из наборов данных xTrain и yTrain и попутно рассчитать среднюю стоимость этих прогнозов.
На данном этапе мы просто позволяем нашему нанонейрону высказать свое мнение, просто позволив ему угадать, как преобразовать температуру. Здесь это может быть глупо неправильно. Средняя стоимость покажет нам, насколько неверна наша модель прямо сейчас. Это значение стоимости действительно важно, поскольку необходимо изменить параметры NanoNeuron w и b и снова выполнить прямое распространение; мы сможем оценить, стал ли наш НаноНейрон умнее или нет после изменения этих параметров.
Средняя стоимость будет рассчитана по следующей формуле:
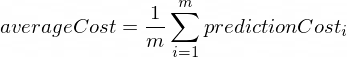
Где m — количество обучающих примеров (в нашем случае: 100 ).
Вот как мы можем реализовать это в коде:
function forwardPropagation ( model , xTrain , yTrain ) {
const m = xTrain . length ;
const predictions = [ ] ;
let cost = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
const prediction = nanoNeuron . predict ( xTrain [ i ] ) ;
cost += predictionCost ( yTrain [ i ] , prediction ) ;
predictions . push ( prediction ) ;
}
// We are interested in average cost.
cost /= m ;
return [ predictions , cost ] ;
}Когда мы знаем, насколько верны или ошибочны прогнозы нашего нанонейрона (на основе средней стоимости на данный момент), что нам следует сделать, чтобы сделать прогнозы более точными?
Обратное распространение дает нам ответ на этот вопрос. Обратное распространение — это процесс оценки стоимости прогнозирования и корректировки параметров нанонейрона w и b чтобы следующие и будущие прогнозы были более точными.
Это то место, где машинное обучение выглядит как волшебство ?♂️. Ключевым понятием здесь является производная , которая показывает, какой шаг нужно сделать, чтобы приблизиться к минимуму функции стоимости.
Помните, что нахождение минимума функции стоимости является конечной целью процесса обучения. Если мы найдем такие значения для w и b , что наша средняя функция стоимости будет небольшой, это будет означать, что модель NanoNeuron делает действительно хорошие и точные прогнозы.
Деривативы — это большая и отдельная тема, которую мы не будем рассматривать в этой статье. MathIsFun — хороший ресурс, позволяющий получить базовое представление о нем.
Одна вещь о производных, которая поможет вам понять, как работает обратное распространение, заключается в том, что производная по своему значению представляет собой касательную линию к кривой функции, которая указывает в направлении минимума функции.
Источник изображения: MathIsFun
Например, на графике выше вы можете видеть, что если мы находимся в точке (x=2, y=4) , то наклон говорит нам идти left и down чтобы добраться до минимума функции. Также обратите внимание, что чем больше наклон, тем быстрее нам следует двигаться к минимуму.
Производные нашей функции averageCost для параметров w и b выглядят следующим образом:
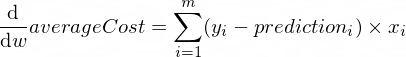
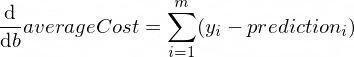
Где m — количество обучающих примеров (в нашем случае: 100 ).
Подробнее о правилах производных и о том, как получить производную сложных функций, можно прочитать здесь.
function backwardPropagation ( predictions , xTrain , yTrain ) {
const m = xTrain . length ;
// At the beginning we don't know in which way our parameters 'w' and 'b' need to be changed.
// Therefore we're setting up the changing steps for each parameters to 0.
let dW = 0 ;
let dB = 0 ;
for ( let i = 0 ; i < m ; i += 1 ) {
dW += ( yTrain [ i ] - predictions [ i ] ) * xTrain [ i ] ;
dB += yTrain [ i ] - predictions [ i ] ;
}
// We're interested in average deltas for each params.
dW /= m ;
dB /= m ;
return [ dW , dB ] ;
} Теперь мы знаем, как оценить корректность нашей модели для всех примеров обучающего набора ( прямое распространение ). Мы также знаем, как делать небольшие корректировки параметров w и b нашей модели NanoNeuron ( обратное распространение ). Но проблема в том, что если мы запустим прямое распространение, а затем обратное распространение только один раз, нашей модели будет недостаточно изучить какие-либо законы/тенденции на основе обучающих данных. Вы можете сравнить это с однодневным посещением ребенком начальной школы. Он/она должен ходить в школу не один раз, а день за днём и год за годом, чтобы чему-то научиться.
Поэтому нам нужно много раз повторить прямое и обратное распространение для нашей модели. Именно это и делает функция trainModel() . Это своего рода «учитель» для нашей модели NanoNeuron:
epochs ) с нашей немного глупой моделью NanoNeuron и попытается обучить ее,xTrain и yTrain ),alpha Несколько слов о скорости обучения alpha . Это всего лишь множитель для значений dW и dB , которые мы вычислили во время обратного распространения. Итак, производная указала нам направление, в котором нам нужно двигаться, чтобы найти минимум функции стоимости (знак dW и dB ), а также показала, насколько быстро нам нужно двигаться в этом направлении (абсолютные значения dW и dB ). Теперь нам нужно умножить эти размеры шагов на alpha , чтобы скорректировать наше движение до минимума быстрее или медленнее. Иногда, если мы используем большие значения для alpha , мы можем просто перепрыгнуть через минимум и никогда его не найти.
Аналогия с учителем заключается в том, что чем сильнее он/она давит на нашего «нано-ребенка», тем быстрее наш «нано-ребенок» будет учиться, но если учитель будет давить слишком сильно, у «ребенка» произойдет нервный срыв, и он выиграет. ты не сможешь ничему научиться?
Вот как мы собираемся обновить параметры w и b нашей модели:
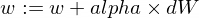
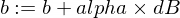
А вот наша функция тренера:
function trainModel ( { model , epochs , alpha , xTrain , yTrain } ) {
// The is the history array of how NanoNeuron learns.
const costHistory = [ ] ;
// Let's start counting epochs.
for ( let epoch = 0 ; epoch < epochs ; epoch += 1 ) {
// Forward propagation.
const [ predictions , cost ] = forwardPropagation ( model , xTrain , yTrain ) ;
costHistory . push ( cost ) ;
// Backward propagation.
const [ dW , dB ] = backwardPropagation ( predictions , xTrain , yTrain ) ;
// Adjust our NanoNeuron parameters to increase accuracy of our model predictions.
nanoNeuron . w += alpha * dW ;
nanoNeuron . b += alpha * dB ;
}
return costHistory ;
}Теперь давайте воспользуемся функциями, которые мы создали выше.
Давайте создадим экземпляр нашей модели NanoNeuron. В этот момент НаноНейрон не знает, какие значения следует установить для параметров w и b . Итак, давайте настроим w и b случайным образом.
const w = Math . random ( ) ; // i.e. -> 0.9492
const b = Math . random ( ) ; // i.e. -> 0.4570
const nanoNeuron = new NanoNeuron ( w , b ) ;Создавайте обучающие и тестовые наборы данных.
const [ xTrain , yTrain , xTest , yTest ] = generateDataSets ( ) ; Давайте обучим модель небольшими шагами ( 0.0005 ) в течение 70000 эпох. С этими параметрами можно поиграть, они определяются опытным путем.
const epochs = 70000 ;
const alpha = 0.0005 ;
const trainingCostHistory = trainModel ( { model : nanoNeuron , epochs , alpha , xTrain , yTrain } ) ;Давайте проверим, как менялась функция стоимости в ходе обучения. Мы ожидаем, что стоимость после обучения будет намного ниже, чем раньше. Это означало бы, что NanoNeuron стал умнее. Возможно и обратное.
console . log ( 'Cost before the training:' , trainingCostHistory [ 0 ] ) ; // i.e. -> 4694.3335043
console . log ( 'Cost after the training:' , trainingCostHistory [ epochs - 1 ] ) ; // i.e. -> 0.0000024 Вот как стоимость обучения меняется с течением эпох. По осям x указан номер эпохи x1000.
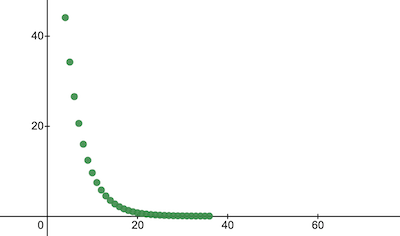
Давайте посмотрим на параметры NanoNeuron, чтобы увидеть, чему он научился. Мы ожидаем, что параметры NanoNeuron w и b будут аналогичны тем, которые у нас есть в функции celsiusToFahrenheit() ( w = 1.8 и b = 32 ), поскольку наш NanoNeuron пытался имитировать его.
console . log ( 'NanoNeuron parameters:' , { w : nanoNeuron . w , b : nanoNeuron . b } ) ; // i.e. -> {w: 1.8, b: 31.99}Оцените точность модели для набора тестовых данных, чтобы увидеть, насколько хорошо наш нанонейрон справляется с предсказаниями новых неизвестных данных. Ожидается, что стоимость прогнозов на тестовых наборах будет близка к стоимости обучения. Это будет означать, что наш нанонейрон хорошо работает с известными и неизвестными данными.
[ testPredictions , testCost ] = forwardPropagation ( nanoNeuron , xTest , yTest ) ;
console . log ( 'Cost on new testing data:' , testCost ) ; // i.e. -> 0.0000023Теперь, когда мы видим, что наш «ребенок» нанонейрона хорошо показал себя в «школе» во время обучения и что он может правильно конвертировать температуру по Цельсию в температуру по Фаренгейту, даже для данных, которые он не видел, мы можем назвать его «умным» и задать ему несколько вопросов. Это была конечная цель всего тренировочного процесса.
const tempInCelsius = 70 ;
const customPrediction = nanoNeuron . predict ( tempInCelsius ) ;
console . log ( `NanoNeuron "thinks" that ${ tempInCelsius } °C in Fahrenheit is:` , customPrediction ) ; // -> 158.0002
console . log ( 'Correct answer is:' , celsiusToFahrenheit ( tempInCelsius ) ) ; // -> 158Так близко! Как и все мы, люди, наш НаноНейрон хорош, но не идеален :)
Приятного вам обучения!
Вы можете клонировать репозиторий и запустить его локально:
git clone https://github.com/trekhleb/nano-neuron.git
cd nano-neuronnode ./NanoNeuron.jsСледующие концепции машинного обучения были пропущены и упрощены для простоты объяснения.
Разделение набора данных для обучения/тестирования
Обычно у вас есть один большой набор данных. В зависимости от количества примеров в этом наборе вы можете разделить его в пропорции 70/30 для наборов обучения/тестирования. Перед разделением данные в наборе должны быть случайным образом перетасованы. Если количество примеров велико (т. е. миллионы), то разделение может происходить в пропорциях, близких к 90/10 или 95/5 для наборов данных обучения/тестирования.
Сеть дает силу
Обычно вы не заметите использования только одного автономного нейрона. Сила – в сети таких нейронов. Сеть может изучить гораздо более сложные функции. Сам по себе NanoNeuron больше похож на простую линейную регрессию, чем на нейронную сеть.
Нормализация ввода
Перед обучением было бы лучше нормализовать входные значения.
Векторизованная реализация
Для сетей векторизованные (матричные) вычисления работают гораздо быстрее, чем for циклов. Обычно прямое/обратное распространение работает намного быстрее, если оно реализовано в векторизованной форме и рассчитано, например, с использованием библиотеки Numpy Python.
Минимум функции стоимости
Функция стоимости, которую мы использовали в этом примере, слишком упрощена. Оно должно иметь логарифмические компоненты. Изменение функции стоимости также приведет к изменению ее производных, поэтому на этапе обратного распространения также будут использоваться другие формулы.
Функция активации
Обычно выходные данные нейрона должны передаваться через функцию активации, такую как Sigmoid, ReLU или другие.