algebraic nnhw

Этот репозиторий содержит исходный код для аппаратных архитектур машинного обучения, которым требуется почти половина количества блоков умножения для достижения той же производительности за счет выполнения альтернативных алгоритмов внутреннего продукта, которые обменивают почти половину умножений на дешевые сложения с низкой разрядностью, при этом производя идентичный результат. как обычный внутренний продукт. Это увеличивает теоретическую пропускную способность и пределы вычислительной эффективности ускорителей ML. Полную информацию смотрите в следующей публикации в журнале:

Т.Э. Пог и Н. Николичи, «Быстрые алгоритмы внутреннего продукта и архитектуры для ускорителей глубоких нейронных сетей», в IEEE Transactions on Computers, vol. 73, нет. 2, стр. 495–509, февраль 2024 г., номер документа: 10.1109/TC.2023.3334140.

URL статьи: https://ieeexplore.ieee.org/document/10323219.

Версия в открытом доступе: https://arxiv.org/abs/2311.12224

Аннотация: Мы представляем новый алгоритм под названием «Быстрый внутренний продукт свободного конвейера» (FFIP) и его аппаратную архитектуру, которые улучшают малоизученный быстрый алгоритм внутреннего продукта (FIP), предложенный Виноградом в 1968 году. В отличие от несвязанных алгоритмов минимальной фильтрации Винограда для сверточных слоев, FIP применим ко всем слоям модели машинного обучения (ML), которые в основном могут разлагаться на умножение матриц, включая полносвязные, сверточные, рекуррентные и уровни внимания/трансформера. Мы впервые реализуем FIP в ускорителе машинного обучения, а затем представляем наш алгоритм FFIP и обобщенную архитектуру, которые по своей сути улучшают тактовую частоту FIP и, как следствие, пропускную способность при аналогичной стоимости оборудования. Наконец, мы вносим оптимизацию для алгоритмов и архитектур FIP и FFIP, ориентированную на машинное обучение. Мы показываем, что FFIP может быть легко интегрирован в традиционные ускорители ML систолической матрицы с фиксированной точкой для достижения той же пропускной способности с половиной количества блоков умножения-накопления (MAC) или может удвоить максимальный размер систолической матрицы, который может поместиться на устройствах с фиксированный аппаратный бюджет. Наша реализация FFIP для неразреженных моделей машинного обучения с входными данными с фиксированной запятой от 8 до 16 бит обеспечивает более высокую пропускную способность и эффективность вычислений, чем лучшие в своем классе предыдущие решения на вычислительной платформе того же типа.

На следующей диаграмме показан обзор системы ускорителя машинного обучения, реализованной в этом исходном коде:

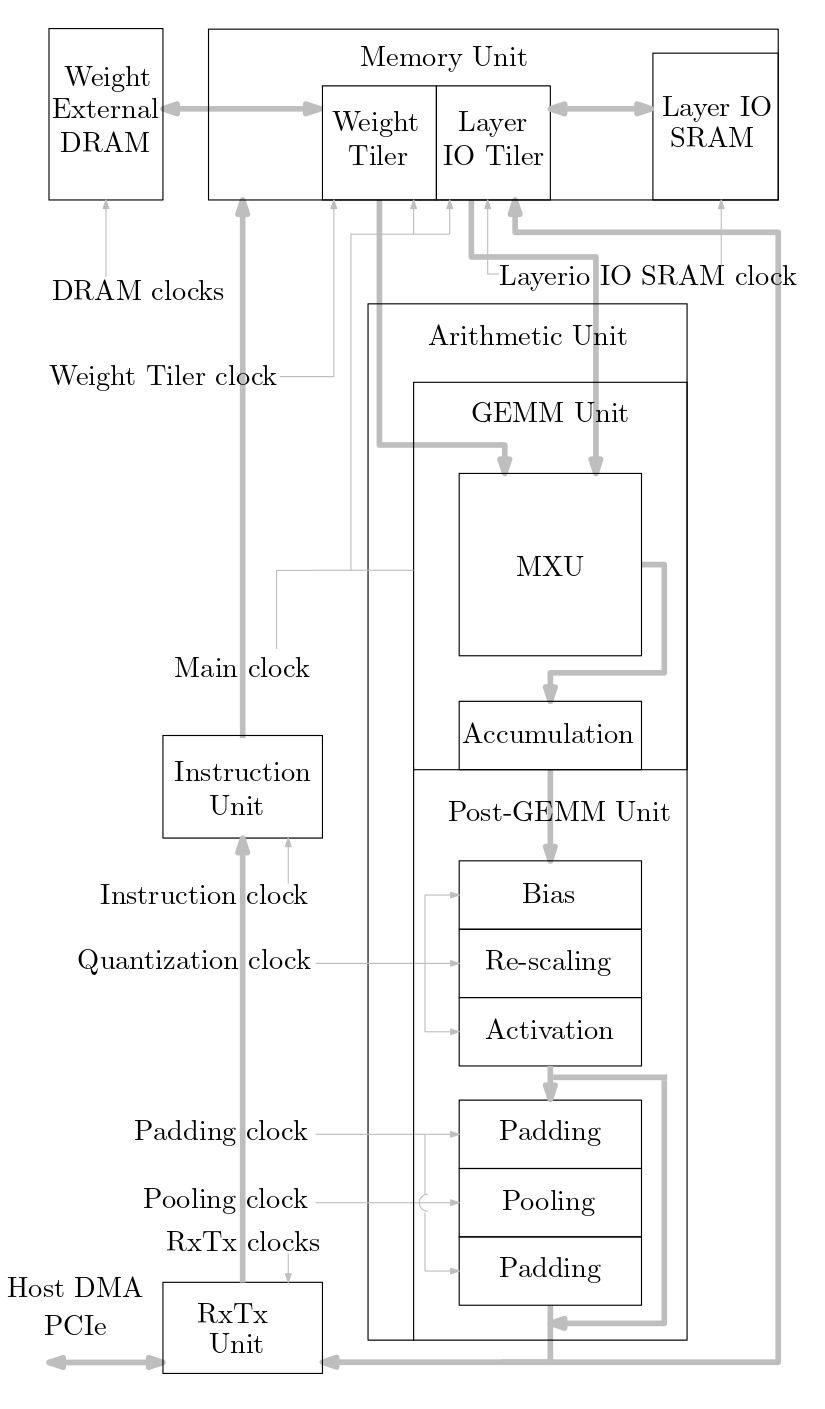
Систолический массив FIP и FFIP/элементы обработки (PE) MXU, показанные ниже в (b) и (c), реализуют алгоритмы внутреннего продукта FIP и FFIP, и каждый по отдельности обеспечивает ту же эффективную вычислительную мощность, что и два базовых PE, показанных в ( а) комбинированные, которые реализуют базовый внутренний продукт, как и в предыдущих ускорителях ML с систолической решеткой:

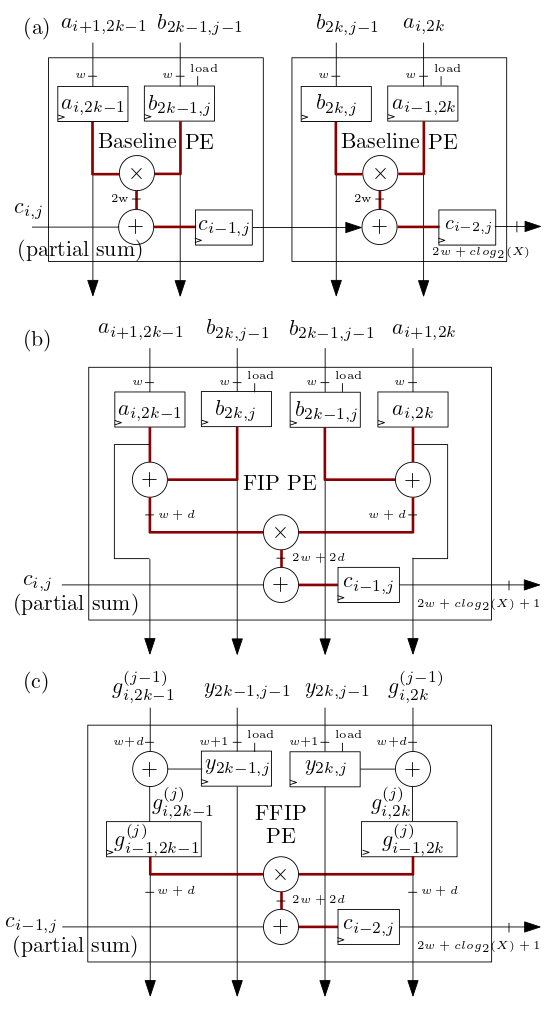
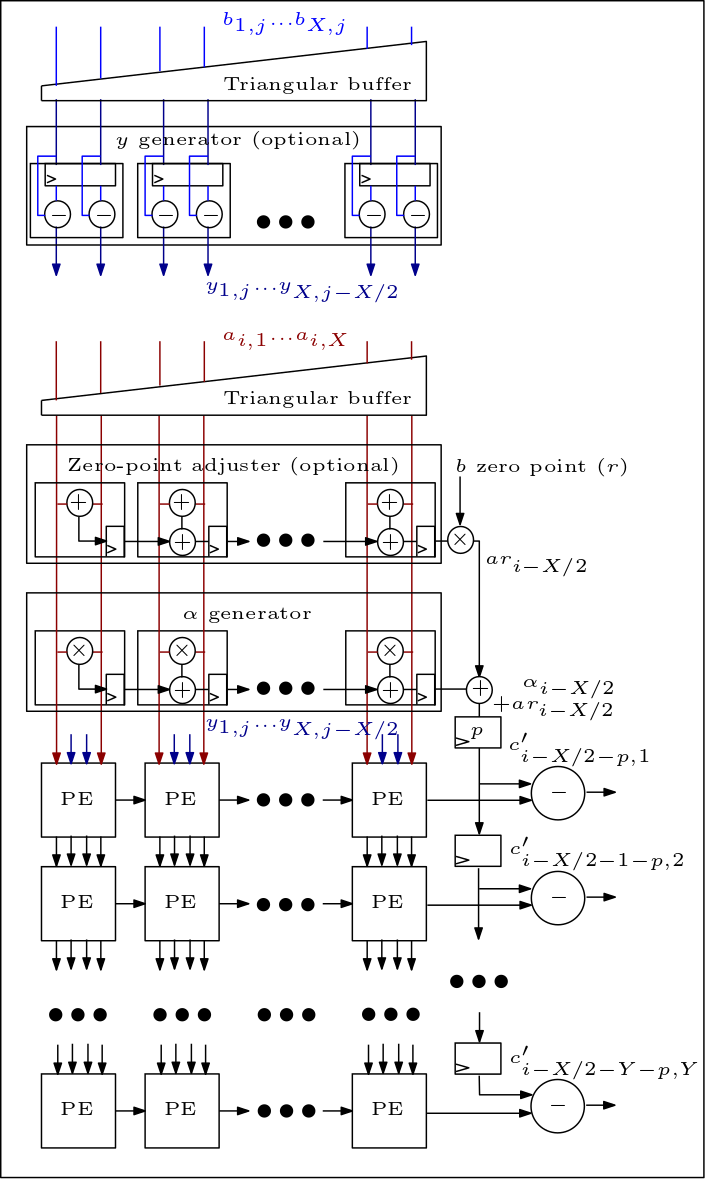
Ниже представлена ​​диаграмма MXU/систолического массива, на которой показано подключение PE:

Организация исходного кода следующая:

• компилятор
  • Компилятор для анализа описаний моделей Python в инструкции ускорителя, которые позволяют ускорить модель. Эта часть также включает в себя код для взаимодействия с драйвером PCIe для запуска выполнения модели на ускорителе, считывания результатов и счетчиков производительности, а также проверки правильности результатов.
• ртл
  • Синтезируемая системаVerilog RTL.
• сим
  • Скрипты для настройки среды моделирования для тестирования.
• тесты
  • Исходный код испытательного стенда на основе UVM для проверки ускорителя при моделировании с использованием Cocotb.
• утилиты
  • Дополнительные пакеты Python и сценарии, использованные в этом проекте, созданы автором для общих утилит и средств разработки.

Файлы rtl/top/define.svh и rtl/top/pkg.sv содержат ряд настраиваемых параметров, таких как FIP_METHOD в define.svh, который определяет тип систолического массива (базовый уровень, FIP или FFIP), SZI и SZJ, которые определяют высота/ширина систолического массива и LAYERIO_WIDTH/WEIGHT_WIDTH, которые определяют входные данные битовая ширина.

Каталог rtl/arith включает файлы mxu.sv и mac_array.sv, которые содержат RTL для архитектур систолического массива базового уровня, FIP и FFIP (в зависимости от значения параметра FIP_METHOD).