Инвертировать матрицу с использованием нейронной сети.
Инвертирующие матрицы представляют уникальные проблемы для нейронных сетей, в первую очередь из -за неотъемлемых ограничений при выполнении точных арифметических операций, таких как умножение и деление на активации. Традиционные плотные сети часто нуждаются в помощи с этими задачами, так как они явно не предназначены для обработки сложностей, связанных с инверсией матрицы. Эксперименты, проведенные с помощью простых плотных нейронных сетей, показали значительные трудности с достижением точных матричных инверсий. Несмотря на различные попытки оптимизировать процесс архитектуры и обучения, результаты часто нуждаются в улучшении. Тем не менее, переход к более сложной архитектуре-7-слойной остаточной сети (RESNET)-может привести к заметным улучшениям производительности.
Архитектура Resnet, известная своей способностью изучать глубокие представления с помощью остаточных соединений, оказалась эффективной в борьбе с инверсией матрицы. С миллионами параметров эта сеть может захватывать сложные шаблоны в данных, которые не могут простые модели. Тем не менее, эта сложность составляет стоимость: для эффективного обобщения требуются существенные данные обучения.
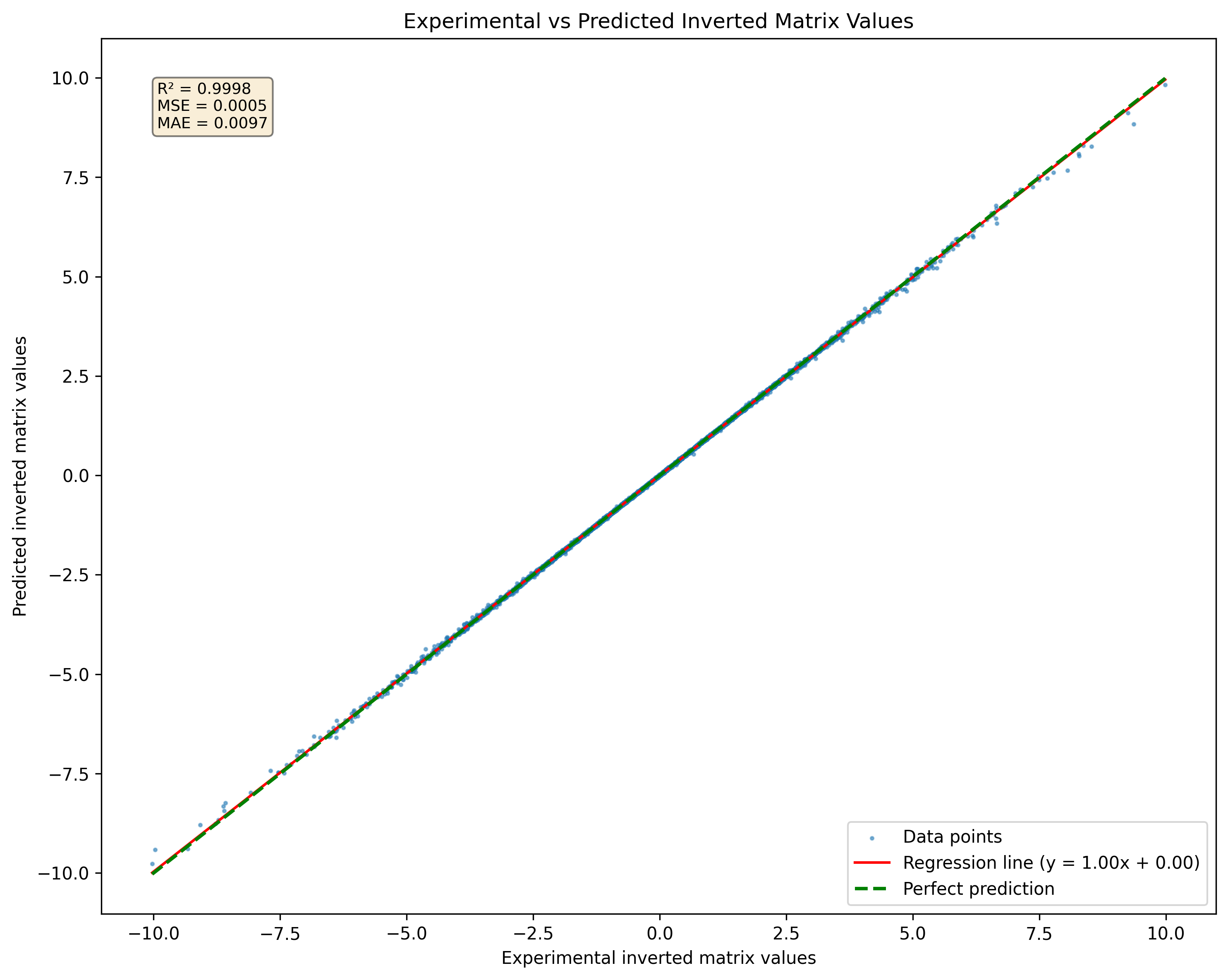Рисунок 1: Визуализация нейронной сети предсказала перевернутую матрицу для набора матриц 3x3, никогда не наблюдаясь в наборе данных
Чтобы оценить эффективность нейронной сети в прогнозировании инверсий матрицы, используется конкретная функция потерь:
В этом уравнении:
Цель состоит в том, чтобы минимизировать разницу между матрицей идентификации и продуктом оригинальной матрицы и ее прогнозируемой обратной. Эта функция потери эффективно измеряет, насколько близко прогнозируемые обратные - точнее.
Кроме того, если
Эта функция потерь предлагает различные преимущества по сравнению с традиционными функциями потерь, таких как средняя квадратная ошибка (MSE) или средняя абсолютная ошибка (MAE).
Прямое измерение точности инверсии Основная цель инверсии матрицы состоит в том, чтобы гарантировать, что произведение матрицы и ее обратная дача матрицы идентичности. Функция потерь непосредственно отражает это требование, измеряя отклонение от матрицы идентификации. Напротив, MSE и MAE сосредоточены на различиях между прогнозируемыми значениями и истинными значениями без явного устранения фундаментального свойства инверсии матрицы.
Акцент на структурной целостности с использованием функции потерь, которая оценивает, насколько близко продукт AA -1AA -1 к II, он подчеркивает поддержание структурной целостности вовлеченных матриц. Это особенно важно в приложениях, где сохранение линейных отношений имеет решающее значение. Традиционные функции потерь, такие как MSE и MAE, не учитывают этот структурный аспект, что потенциально приводит к решениям, которые минимизируют ошибку, но не могут удовлетворить математические требования инверсии матрицы.
Применимость к не-соседним матрицам эта функция потери по своей природе предполагает, что инвертированные матрицы не являются не-сингловальными (т.е., перемещенные). В сценариях, где присутствуют единственные матрицы, традиционные функции потерь могут привести к вводящим в заблуждение результатам, поскольку они не учитывают невозможность получения действительного обратного. Предложенная функция потерь подчеркивает это ограничение, создавая большие ошибки при попытке инвертировать единственные матрицы.
Одним из значительных ограничений при использовании нейронных сетей для матричной инверсии является их неспособность эффективно обрабатывать единственные матрицы. У единственной матрицы нет обратного; Таким образом, любая попытка нейронной сети предсказать обратное для таких матриц даст неверные результаты. На практике, если во время обучения или вывода представлена единственная матрица, сеть может по -прежнему вывести результат, но этот выход не будет действительным или значимым. Это ограничение подчеркивает важность обеспечения того, чтобы данные обучения состояли из не-симулярных матриц, когда это возможно.
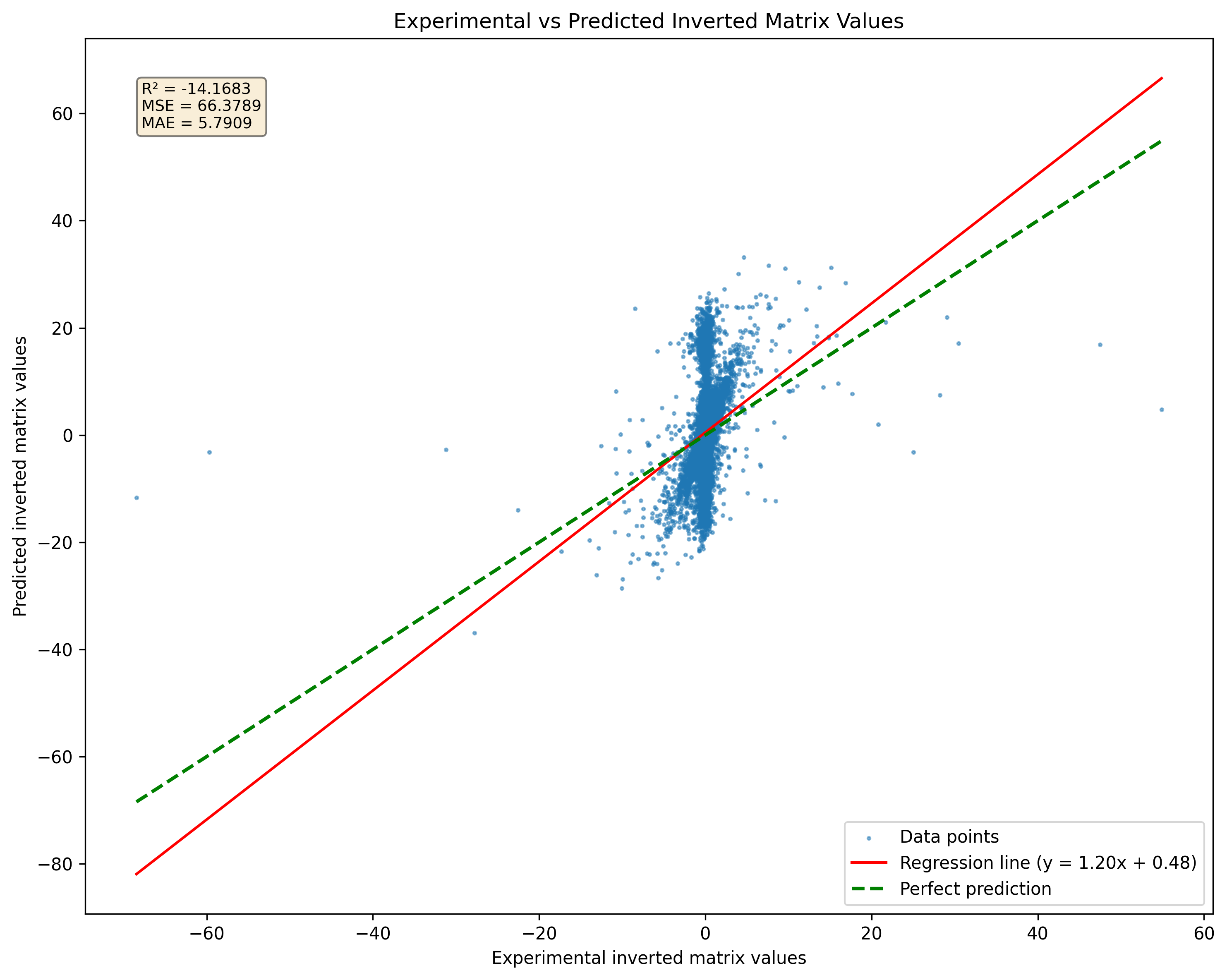Рисунок 2: Сравнение прогнозирования модели для сингулярных матриц по сравнению с псевдоинверсиями. Обратите внимание, что модель даст результаты независимо от матричной сингулярности.
Исследования показывают, что модель Resnet может запомнить хорошее количество образцов без значительной потери точности. Тем не менее, увеличение размера набора данных до 10 миллионов образцов может привести к серьезному переоснащению. Этот переосмысление происходит, несмотря на большой объем данных, подчеркивая, что простое увеличение размера набора данных не гарантирует улучшения обобщения для сложных моделей. Чтобы решить эту проблему, может быть принята стратегия непрерывной генерации данных. Вместо того, чтобы полагаться на статический набор данных, образцы могут генерироваться на лету и подавать в сеть по мере их создания. Этот подход, который имеет решающее значение при смягчении переосмысления, не только обеспечивает разнообразные примеры обучения, но и гарантирует, что модель подвергается воздействию постоянно развивающегося набора данных.
Таким образом, хотя инверсия матрицы по своей сути сложна для нейронных сетей из -за ограничений в арифметических операциях, использование передовых архитектур, таких как Resnet, может дать лучшие результаты. Тем не менее, необходимо уделять тщательное рассмотрение требований к данным и переосмысления. Непрерывное генерирование обучающих образцов может улучшить процесс обучения модели и повысить производительность в задачах инверсии матрицы. Эта версия поддерживает безличный тон, обсуждая проблемы и стратегии в обучении нейронных сетей для инверсии матрицы.
DeepMatrixinversion распределяется по лицензии LGPLV3
Чтобы узнать больше подробно, как работают лицензии, прочитайте файл «Лицензия» или перейдите на «http://www.gnu.org/licenses/lgpl-3.0.html»
DeepMatrixinversion в настоящее время является собственностью Джузеппе Марко Рандаццо.
Чтобы установить репозиторий DeepMatrixinversion, вы можете выбрать между использованием поэзии, PIP или PIPX ниже представлены инструкции для обоих методов.
git clone https://github.com/gmrandazzo/DeepMatrixInversion.git
cd DeepMatrixInversion
python3 -m venv .venv
. .venv/bin/activate
pip install poetry
poetry install
Это настроит вашу среду со всеми необходимыми пакетами для запуска DeepMatrixinversion.
Создайте виртуальную среду и установите deppmatrixinversion с помощью PIP
python3 -m venv .venv
. .venv/bin/activate
pip install git+https://github.com/gmrandazzo/DeepMatrixInversion.git
Если вы предпочитаете использовать PIPX, который позволяет устанавливать приложения Python в изолированных средах, выполните следующие действия:
python3 -m pip install --user pipx
apt-get install pipx
brew install pipx
sudo dnf install pipx
PIPX Установка git+https: //github.com/gmrandazzo/deepmatrixinversion.git
Чтобы обучить модель, которая может выполнять инверсию матрицы, вы будете использовать команду DMXTRAIN. Эта команда позволяет вам указать различные параметры, которые контролируют процесс обучения, такие как размер матриц, диапазон значений и продолжительность обучения.
dmxtrain --msize < matrix_size > --rmin < min_value > --rmax < max_value > --epochs < number_of_epochs > --batch_size < size_of_batches > --n_repeats < number_of_repeats > --mout < output_model_path > dmxtrain --msize --rmin -1 --rmax 1 --epochs 5000 --batch_size 1024 --n_repeats 3 --mout ./Model_3x3
--msize <matrix_size>: Specifies the size of the square matrices to be generated for training. For example, 3 for 3x3 matrices.
--rmin <min_value>: Sets the minimum value for the random elements in the matrices. For instance, -1 will allow negative values.
--rmax <max_value>: Sets the maximum value for the random elements in the matrices. For example, 1 will limit values to a maximum of 1.
--epochs <number_of_epochs>: Defines how many epochs (complete passes through the training dataset) to run during training. A higher number typically leads to better performance; in this case, 5000.
--batch_size <size_of_batches>: Determines how many samples are processed before the model is updated. A batch size of 1024 means that 1024 samples are used in each iteration.
--n_repeats <number_of_repeats>: Indicates how many times to repeat the training process with different random seeds or initializations. This can help ensure robustness; for instance, repeating 3 times.
--mout <output_model_path>: Specifies where to save the trained model. In this example, it saves to ./Model_3x3.
После того, как вы обучили свою модель, вы можете использовать ее для выполнения инверсии матрицы на новых входных матрицах. Команда для вывода - dmxinvert, которая принимает входную матрицу и выводит ее обратную.
Предупреждение: dmxinvert может инвертировать матрицу, больше, чем та, которая используется для обучения модели через формулу инверсии блока блока Шермана-Моррисон-Вудбери. Эта функция работает только с матрицами, размер блока, размер блока, размер обучающего блока модели без напоминания. Эта функция очень экспериментальная и может потребоваться пересмотреть.
dmxinvert --inputmx <input_matrix_file> --inverseout <output_csv_file> --model <model_path>
dmxinvert --inputmx input_matrix.csv --inverseout output_inverse.csv --model ./Model_3x3_*
--inputmx <input_matrix_file>: Specifies the path to the input matrix file that you want to invert. This file should contain a valid matrix format (e.g., CSV).
--inverseout <output_csv_file>: Indicates where to save the resulting inverted matrix. The output will be saved in CSV format.
--model <model_path>: Provides the path to the trained model that will be used for performing the inversion.
Сгенерирование искусственного набора данных с входной матрицей и выводом переворачивается
dmxdatasetgenerator 3 10 -1 1 test_3x3_range_-1+1
Это генерирует 10 матриц размера 3x3 с числами в диапазоне от -1 до +1.
dmxdatasetgenerator [matrix size] [number of samples] [range min] [range max] [outname_prefix]
Затем набор данных может быть подтвержден с помощью dmxdatasetVerify
dmxdatasetverify test_3x3_range_-1+1_matrices_3x3.mx test_3x3_range_-1+1_matrices_inverted_3x3.mx invertible
Dataset valid.
dmxdatasetverify [dataset matrix to invert] [dataset matrix inverted] [type: invertible or singular]
Файл ввода матрицы должен быть отформатирован следующим образом:
0.24077047370124594,-0.5012474139608847,-0.5409542929032876
-0.6257864520097793,-0.030705148203584942,-0.13723920334288975
-0.48095686716222064,0.19220406568380666,-0.34750000491973854
END
0.4575368007107925,0.9627977617090073,-0.4115240560547333
0.5191433428806012,0.9391491187187144,-0.000952683255491138
-0.17757763984424968,-0.7696584771443977,-0.9619759413623306
END
-0.49823271153034154,0.31993947803488587,0.9380291202366384
0.443652116558352,0.16745965310481048,-0.267270356721347
0.7075720067281346,-0.3310912886946993,-0.12013367141105102
END
Каждый блок чисел представляет собой отдельную матрицу, за которой следует конечный маркер, указывающий на конец этой матрицы.
