
и задачах Fiber в React, а разные задачи Fiber имеют разные приоритеты. React должен сначала обрабатывать задачи с высоким приоритетом. Например, клики и действия пользователя являются высокоприоритетными задачами, поскольку действия пользователя определенно будут иметь немедленный эффект и улучшат взаимодействие с пользователем. Например, приоритет событий анимации должен быть ниже. После того как новая задача с высоким приоритетом попадает в очередь, React должен сначала ее обработать.
Для хранения этих задач в React есть два пула задач.
// Задачи хранятся в минимальной куче вар TaskQueue = []; var timerQueue = [];
TaskQueue и timerQueue — оба массива. Первый хранит задачи, которые необходимо выполнить немедленно, а второй — задачи, которые можно отложить.
вар newTask = {
id: TaskIdCounter++, // Отмечаем идентификатор задачи
callback, // функция обратного вызова PriorityLevel, // приоритет задачи startTime, // время начала задачи, момент времени expirationTime, // время истечения срока действия, момент времени sortIndex: -1, // сортировка задачи, значение берется из времени истечения, поэтому значение Чем меньше значение, тем выше приоритет}; Как только в React появится новая задача, она сначала будет использовать currentTime для записи текущего времени (performance.now() или Date.now()). параметр задержки, то время начала выполнения задачи = currentTime + задержка;. Далее, если установлено startTime > currentTime, это доказывает, что задачу можно отложить, тогда задача попадает в timerQueue, иначе — в TaskQueue.
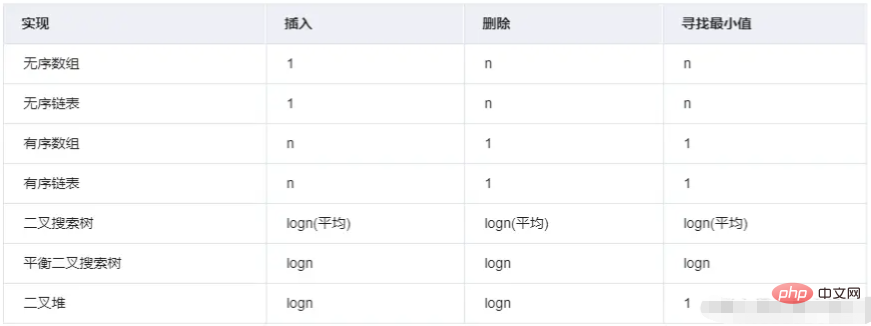
Как React находит задачу с наивысшим приоритетом. Возьмем, к примеру, TaskQueue. Это динамический пул задач (очередь задач), а форма данных — массив. Конечно, можно сортировать по приоритету, то есть Array.sort. Когда в очередь добавляется новая задача, сначала она сортируется, а затем находится и выполняется задача с наивысшим приоритетом. Но средняя временная сложность Array.sort равна O(nlogn), что не является лучшим решением.
SortIndex используется для сортировки в newTask TaskQueue. Это значение берется из времени истечения, а это означает, что чем выше приоритет задачи, тем больше ее нужно понять и выполнить, поэтому время истечения будет меньше. выше приоритет, время истечения срока действия. Чем меньше время, тем меньше будет sortIndex. По сути, это приоритетная очередь .
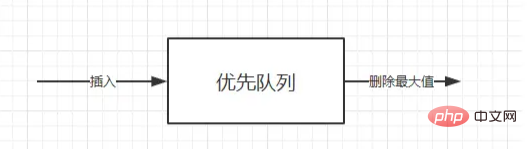
Приоритетная очередь — это тоже разновидность очереди ( во-первых, это очередь, во-вторых, хвостовой вход — первый выход ). Единственное отличие состоит в том, что порядок выхода из приоритетной очереди в некоторых случаях основан на приоритете; , вам может потребоваться найти минимальный или максимальный элемент в наборе элементов, которым можно управлять с помощью АТД очереди приоритетов. АТД очереди приоритетов — это структура данных, которая поддерживает операции вставки и удаления минимального значения (возврат и удаление минимального элемента) или. удаление операции максимального значения (возврат и удаление минимального элемента, удаление самого большого элемента).
Если элемент с наименьшим значением ключа имеет наивысший приоритет, то эта очередь с приоритетом называется очередью с возрастающим приоритетом (т. е. первым всегда удаляется наименьший элемент). Аналогично, если элемент с наибольшим значением ключа имеет наивысший приоритет, то этот тип приоритетной очереди называется очередью с нисходящим приоритетом (т. е. первым всегда удаляется самый большой элемент, поскольку эти два типа симметричны, вам нужно только); сосредоточиться на одном из них, например на очереди с возрастающим приоритетом.
Например : когда мы покупали билеты, мы все стояли в очереди и имели одинаковый приоритет. Тот, кто был перед очередью, покупал билет первым, но затем приходил солдат, и у него был более высокий приоритет, и он находился прямо в очереди. .Фронт.
Минимальная куча (маленькая корневая куча, небольшая верхняя куча...) используется в React для достижения этой функции. То есть превратить TaskQueue в минимальную кучу, затем извлечь верхнюю задачу для выполнения, создать кучу TaskQueue и сохранить ее как структуру данных с минимальной кучей. При вставке новой задачи в TaskQueue ее также необходимо создавать в куче и всегда сохранять минимальную кучу.
: В некоторых местах кучу называют очередью с приоритетом (неточно). Прежде всего, это очередь и имеет характеристики очереди, то есть « первым пришел — первым вышел ». . Во-вторых, элементы в этой очереди имеют приоритеты, и элементы с более высоким приоритетом будут ранжироваться первыми.
Если быть точным, куча — это способ реализации очереди с приоритетами. Конечно, очереди с приоритетами можно реализовать и другими способами.
Ранее мы говорили, что сортировка кучей — это нестабильная сортировка, но TaskQueue надеется, что этот процесс стабилен. То есть, если возможно, что время истечения двух задач одинаково, то это зависит от того, кто входит. во-первых, пул задач — это значение идентификатора newTask. Каждый раз, когда приходит новая задача, идентификатор увеличивается на 1.
функция сравнения(а, б) {
// Сначала сравниваем индекс сортировки, затем идентификатор задачи.
const diff = a.sortIndex - b.sortIndex;
вернуть разницу !== 0 ?
} Прежде чем понять, что такое минимальная куча, давайте повторим базовые знания.
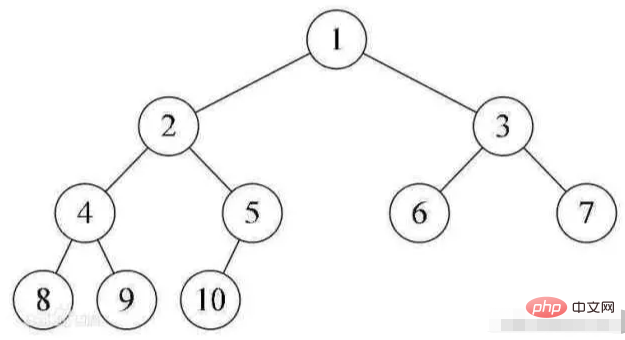
— это упорядоченное дерево, в котором степень узлов не превышает 2. Это самое простое и важное дерево.
— это двоичное дерево, в котором все узлы на каждом уровне имеют по два дочерних узла, за исключением последнего уровня, у которого нет дочерних узлов.
С графической точки зрения полное двоичное дерево выглядит как треугольник.
Если количество уровней двоичного дерева равно K, а общее количество узлов равно (2^k)-1, то это полное двоичное дерево.
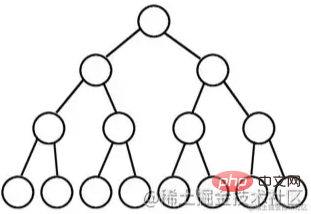
Полное двоичное дерево означает «дочерние элементы имеют обе стороны» и является очень совершенным, поэтому его называют полным двоичным деревом.
исключая листовые узлы, степень всех узлов равна 2. Другими словами, степень всех узлов может быть только 0 или 2.
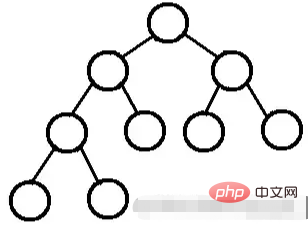
Идеальное двоичное дерево либо не имеет дочерних элементов, либо имеет обоих дочерних элементов.
Оригинальный английский текст полного двоичного дерева:
Полное двоичное дерево (FBT) — это дерево, в котором каждый узел, кроме листьев, имеет двух дочерних элементов.
Исходный английский текст идеального двоичного дерева:
Идеальное двоичное дерево (PBT) — это дерево, все листовые узлы которого находятся на одной и той же глубине. Все внутренние узлы имеют степень 2.
Все зарубежные книги ссылаются на самые ранние переведенные учебники по полным бинарным деревьям и совершенным бинарным деревьям, но самые ранние переведенные статьи переведены неправильно. Сейчас в Китае мы можем совершать ошибки только тогда, когда они неправы (все неправы, значит, неправильный тоже прав. Например, лоббисты...). Если вы хотите обсудить эти две концепции с зарубежными друзьями, вам следует обратить на это внимание.
двоичное дерево (CBT) — это двоичное дерево, в котором каждый уровень, за исключением, возможно, последнего, полностью заполнен, а все узлы расположены максимально слева.
Бинарное дерево с n узлами глубины k, пронумеруйте узлы в. дерево сверху вниз и слева направо. Если узел с номером i (1≤i≤n) находится в двоичном дереве с узлом с номером i в полном двоичном дереве, если позиции одинаковы, бинарное дерево. называется полным двоичным деревом.
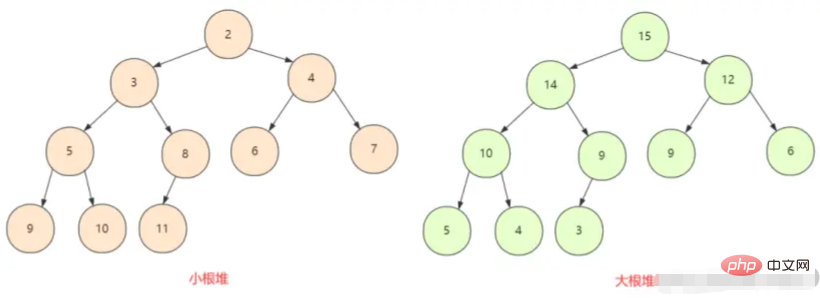
Куча всегда удовлетворяет следующим свойствам:
сначала мы должны понять, что такое большая корневая куча; небольшая корневая куча. В полном двоичном дереве все узлы больше (или меньше), чем их дочерние узлы, поэтому здесь есть две ситуации: максимальная куча и минимальная куча.
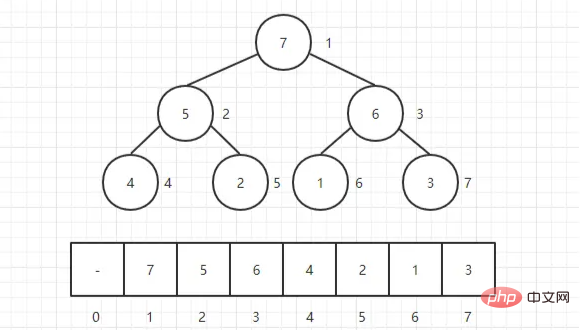
Куча обычно представляет собой массив объектов, который можно рассматривать как полное двоичное дерево . Конечно, двоичные деревья также могут быть представлены массивами.
— сначала построить кучу, а затем настроить ее.
для двоичного дерева (представление массива), мы проводим настройку снизу вверх, начиная с «первого нелистового узла» и продвигаясь вперед. Правила настройки следующие:
Построение кучи — это O(n). ) процесс временной сложности.
① Начните с первого нелистового узла, чтобы оценить обмен вниз (shiftDown), чтобы текущий узел и дочерний узел могли сохранить свойства кучи
. ② Однако обычная замена узла может не стать проблемой, если обмен нарушает свойства структуры кучи. дочернего элемента, то его необходимо повторно нажать ShiftDown на замененном узле до тех пор, пока он не будет остановлен.
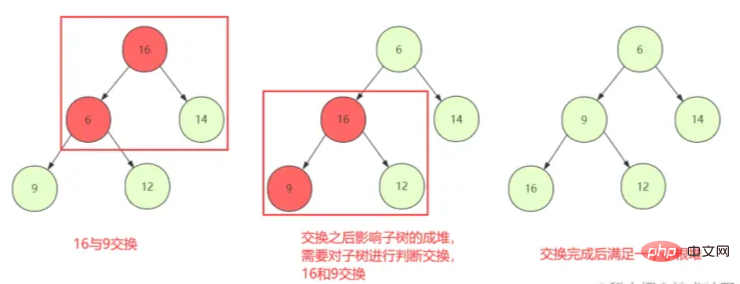
кучи
разрушить структуру кучи.
① Просто поместите последний элемент первым. Таким образом, вам нужно оценить только сдвиг подкачки (shiftDown), но нужно отметить, что в это время изменился размер всей кучи. Логически мы не будем использовать отброшенную позицию, поэтому нам нужно включить кучу. параметр size при разработке функции.
② Повторяйте описанную выше операцию, пока не будут получены все элементы кучи.
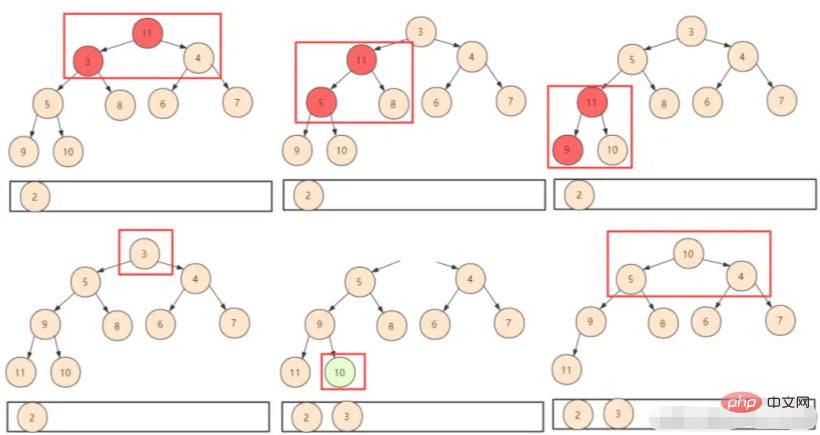
С точки зрения анализа сложности алгоритма кучи, предыдущая сложность времени построения кучи составляла O(n). Каждый раз, когда вершина кучи удаляется, а затем перемещается вниз, номер каждого из них регистрируется. Таким образом, сложность равна O(nlogn), а общая временная сложность равна O(n)+O(nlogn)=O(nlogn).
кучи Куча подходит для сохранения максимальной ценности коллекции.
После того, как элемент извлекается из кучи, стоимость повторной настройки для получения верхнего элемента кучи (то есть второго по величине значения) относительно невелика, поскольку после извлечения элемента куча представляет собой полуфабрикат. -готовый продукт, а второе по величине значение получается из полуфабриката. Конечно, стоимость относительно невелика, а временная сложность равна O(logn), но если пройти его один раз, чтобы найти второе по величине значение, временная сложность равна O(n).
Коднаписан на Javascript ES6.
классКуча {
конструктор (данные, комп) {
это.данные = данные? данные: [];
// Правила сравнения: более гибкие, можно сравнивать значения или объекты this.compartor = comp ? comp : (ab) => ab;
// Настройка кучи (приоритетная очередь)
это.heapify();
}
куча() {
if(this.size() <= 1) return;
// Начинаем настройку с первого нелистового узла или с последнего элемента for(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//Регулировка кучи. Регулировку вниз также можно реализовать с помощью рекурсии. Здесь для реализации this.shiftDown(i);
}
}
// Корректируем сдвиг вниз (i) {
пусть влево = 2*i +1;
пусть вправо = 2*i +2;
пусть len = this.size();
в то время как (я <len) {
пусть findIndex = я;
//Левый дочерний элемент «больше»
if(left < len && this.compartor(this.data[left], this.data[findIndex]) < 0) {
findIndex = слева;
}
// Правый дочерний элемент «больше»
if(right < len && this.compartor(this.data[right], this.data[findIndex]) < 0) {
findIndex = правильно;
}
if(i !== findIndex) {
//Заменяем текущий узел на большее значение [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// После настройки этого слоя это может повлиять на характеристики кучи нижнего уровня, поэтому продолжайте настраивать нижний уровень (итеративная реализация или рекурсивная)
я = найтиИндекс;
слева = 2*я +1;
вправо = 2*я +2;
}
еще {
// Если корректировка не требуется, выпрыгнуть (нужно выскочить, иначе цикл не сможет завершиться)
перерыв;
}
}
}
// Корректируем сдвиг вверх (i){
// Находим нижний индекс родительского элемента letparentIndex = Math.floor((i-1)/2);
// Устанавливаем максимум на 0
while(parentIndex >=0 ) {
пусть findIndex = я;
if(this.compartor(this.data[parentIndex], this.data[findIndex]) > 0) {
findIndex = родительскийиндекс;
}
если (findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
я = найтиИндекс;
родительскийиндекс = Math.floor((i-1)/2);
}
еще {
перерыв;
}
}
}
// Получаем количество всех элементов в куче size(){
вернуть this.data.length;
}
// Получаем первый элемент просмотра кучи(){
if(!this.size()) возвращает ноль;
вернуть this.data[0];
}
//Добавляем элемент в кучу push(x){
this.data.push(x);
this.shiftUp(this.data.length-1);
}
// Извлекаем первый элемент из кучи pop(){
if(!this.size()) возвращает ноль;
пусть res = this.data[0];
если(this.size() == 1) {
это.данные.поп();
}
еще {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
это.shiftDown(0);
}
вернуть разрешение;
}
} let arr = [2,9,8,6,3,10,5,7,4,1];
пусть comp = (a, b) => ab;
пусть куча = новая куча (arr, comp);
пусть рез = [];
в то время как (куча.размер()) {
res.push(куча.pop());
}
console.log(res); Элемент в arr также может быть объектом.
Каталог packages/scheduler в исходном коде React — это код, связанный с модулем планирования задач React.
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
/**
* Авторские права (c) Facebook, Inc. и ее дочерних компаний.
*
* Этот исходный код распространяется по лицензии MIT, которую можно найти в
* Файл LICENSE в корневом каталоге этого исходного дерева.
*
* @flow строгий
*/
тип Heap = Array<Node>;
тип Узел = {|
ID: номер,
сортировкаИндекс: число,
|};
функция экспорта push (куча: Куча, узел: Узел): void {
константный индекс = heap.length;
куча.push(узел);
siftUp(куча, узел, индекс);
}
функция экспорта peek(куча: Куча): Node |
const first = куча[0];
вернуть первый === неопределенное значение null: первый;
}
функция экспорта pop(heap: Heap): Node |
const first = куча[0];
если (первый !== не определено) {
const последний = heap.pop();
if (последний !== первый) {
куча[0] = последний;
siftDown (куча, последний, 0);
}
вернуться первым;
} еще {
вернуть ноль;
}
}
функция siftUp(куча, узел, я) {
пусть индекс = я;
в то время как (истина) {
const родительскийиндекс = (индекс - 1) >>> 1;
константный родитель = куча [parentIndex];
if (родительский !== неопределенное && сравнение(родительский узел) > 0) {
// Родительский объект больше.
куча [parentIndex] = узел;
куча[индекс] = родительский;
индекс = родительскийиндекс;
} еще {
// Родитель меньше.
возвращаться;
}
}
}
функция siftDown(куча, узел, я) {
пусть индекс = я;
константная длина = куча.длина;
while (индекс < длина) {
const leftIndex = (индекс + 1) * 2 - 1;
const left = куча [leftIndex];
const rightIndex = leftIndex + 1;
const right = куча [rightIndex];
// Если левый или правый узел меньше, поменяйте местами меньший из них.
if (left !== undefined && Compare(left, node) <0) {
если (справа !== неопределенно && сравнить(справа, слева) < 0) {
куча[индекс] = правильно;
куча [rightIndex] = узел;
индекс = правыйИндекс;
} еще {
куча [индекс] = слева;
куча [leftIndex] = узел;
индекс = левыйИндекс;
}
} else if (right !== undef && Compare(right, node) < 0) {
куча[индекс] = правильно;
куча [rightIndex] = узел;
индекс = правыйИндекс;
} еще {
// Ни один из дочерних элементов не меньше.
возвращаться;
}
}
}
функция сравнения(а, б) {
// Сначала сравниваем индекс сортировки, затем идентификатор задачи.
const diff = a.sortIndex - b.sortIndex;
вернуть разницу !== 0 ?
} Реализованная нами минимальная куча немного отличается от реализации в React, но идея та же, только код написан по-другому.
планирование задач в React реализовано с использованием минимальной кучи. Если у нас раньше было определенное понимание минимальной кучи, мы изучим этот контент быстрее. Лично я считаю, насколько важно накапливать знания на раннем этапе, но этот процесс может быть скучным. Как вы думаете, сейчас вы знаете какие-то алгоритмы? На самом деле эти алгоритмы начального уровня, а вы еще даже не начали? Потому что в сценарии планирования задач React требования, которые необходимо реализовать, очень ясны, а используемые структуры данных и алгоритмы также ясны. В некоторых реальных сценариях мы знаем конкретные требования, но не знаем, какие данные и алгоритмы использовать. Нам необходимо абстрагировать требования и разработать конкретные структуры данных и алгоритмы на основе абстрактной модели данных. Это ключевые моменты. .