การสุ่มตัวอย่าง Lanczos (อ่านว่า Lanchos) เป็นเทคนิคที่ซับซ้อนสำหรับการสอดแทรกสัญญาณดิจิทัล โดยให้คุณภาพของภาพที่เหนือกว่าเมื่อเปรียบเทียบกับวิธีที่ง่ายกว่า เช่น เพื่อนบ้านที่ใกล้ที่สุดและการแก้ไขแบบไบลิเนียร์ ด้วยการรักษารายละเอียดอย่างมีประสิทธิภาพและลดการสร้างนามแฝงให้เหลือน้อยที่สุด การสุ่มตัวอย่าง Lanczos จึงถูกนำมาใช้กันอย่างแพร่หลายในแอปพลิเคชันการประมวลผลภาพและสัญญาณ
แม้ว่า Lanczos จะเหนือกว่าในด้านคุณภาพของภาพ แต่ก็แลกมาด้วยความซับซ้อนในการคำนวณที่เพิ่มขึ้น นอกจากนี้ ศักยภาพในการ "ส่งเสียง" สิ่งประดิษฐ์ โดยเฉพาะบริเวณขอบแหลมคม อาจเป็นข้อเสียเปรียบได้ แม้จะมีความท้าทายเหล่านี้ Lanczos ยังคงเป็นตัวเลือกที่ต้องการสำหรับงานต่างๆ เช่น การปรับขนาดและการหมุนภาพ เนื่องจากคุณประโยชน์ด้านประสิทธิภาพโดยรวม
เอกสารนี้ให้ภาพรวมที่ครอบคลุมของการสุ่มตัวอย่างใหม่ของ Lanczos รวมถึงรากฐานทางทฤษฎี รายละเอียดการนำไปปฏิบัติ และการใช้งานจริง โดยทำหน้าที่เป็นทรัพยากรอันมีค่าสำหรับนักพัฒนาและนักวิจัยที่ต้องการทำความเข้าใจและใช้เทคนิคอันทรงพลังนี้ ในส่วนต่อๆ มาจะเจาะลึกประเด็นสำคัญของการสุ่มตัวอย่างใหม่ของ Lanczos เช่น เคอร์เนลของ Lanczos กระบวนการประมาณค่าและการสุ่มตัวอย่างใหม่ การเก็บรักษาฟลักซ์ การอัปแซมปลิง การสุ่มตัวอย่างต่ำ การวางตำแหน่งตัวอย่าง ช่วงเอาท์พุต การประมาณค่าแบบหลายมิติ และความสามารถในการแยกส่วน มีตัวอย่างการใช้งานจริงพร้อมซอร์สโค้ดที่แนบมาด้วย
เคอร์เนล Lanczos ที่กำหนดไว้สำหรับขนาดรองรับที่กำหนด เป็นฟังก์ชันที่ใช้ในการสุ่มตัวอย่าง Lanczos ใหม่ เคอร์เนลถูกกำหนดเป็น:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
ที่ไหน:
ฟังก์ชัน sinc ที่ทำให้เป็นมาตรฐานถูกกำหนดเป็น:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
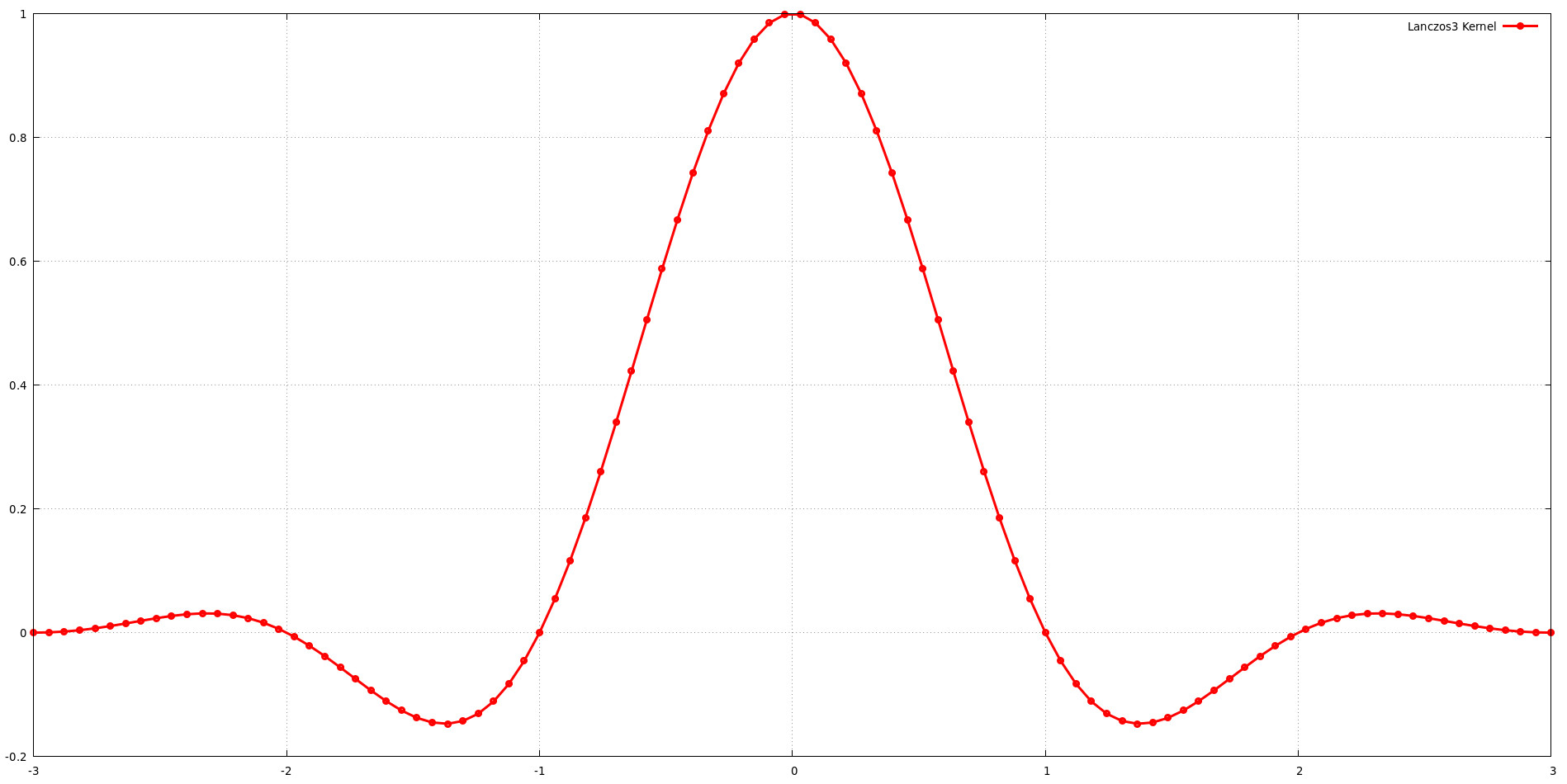
กราฟแสดงรูปร่างของเคอร์เนล Lanczos สำหรับขนาดรองรับ a = 3 ซึ่งหมายความว่าเคอร์เนลมีฟังก์ชัน sinc สามกลีบ แม้ว่าการเพิ่มขนาดการรองรับ (a) โดยทั่วไปจะให้ความยืดหยุ่นมากขึ้นในการกำหนดรูปแบบการตอบสนองความถี่ แต่ยังเพิ่มต้นทุนการคำนวณอีกด้วย ต้องมีความสมดุลระหว่างคุณภาพของภาพและประสิทธิภาพการคำนวณเมื่อเลือกขนาดรองรับ การค้นพบของ Jim Blinn ว่าเคอร์เนล Lanczos ที่มี = 3 ให้ความสมดุลที่ยอดเยี่ยมของการเก็บรักษาความถี่ต่ำและการปฏิเสธความถี่สูงสนับสนุนแนวคิดนี้
หมายเหตุ: คำว่า "ความกว้างเคอร์เนล" "ขนาดรองรับ" และ "ขนาดตัวกรอง" มักใช้สลับกันเพื่ออธิบายพารามิเตอร์ a อย่างไรก็ตาม ในบริบทของการสุ่มตัวอย่างใหม่ของ Lanczos "ขนาดรองรับ" สะท้อนแนวคิดได้แม่นยำที่สุด
การประมาณค่าของ Lanczos เป็นเทคนิคที่ใช้ในการสุ่มตัวอย่างสัญญาณแยกเป็นอัตราการสุ่มตัวอย่างใหม่ โดยสามารถแปลงสัญญาณต้นฉบับด้วยเคอร์เนล Lanczos ได้
สัญญาณอินเทอร์โพเลต s2(x) สามารถคำนวณได้ดังนี้:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
ที่ไหน:
การเก็บรักษาฟลักซ์:
ปัจจัยการทำให้เป็นมาตรฐาน w(x) มีความสำคัญอย่างยิ่งต่อการรักษาพลังงานสัญญาณโดยรวมหรือมวลในระหว่างกระบวนการแก้ไข ช่วยให้มั่นใจได้ว่าผลรวมของค่าที่ประมาณค่าจะใกล้เคียงกับผลรวมของตัวอย่างต้นฉบับ น้ำหนักตัวกรองคำนวณดังนี้:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
การสุ่มตัวอย่าง:
เมื่อเพิ่มอัตราการสุ่มตัวอย่าง สามารถใช้สมการประมาณค่าของ Lanczos ได้โดยตรงโดยไม่ต้องแก้ไข
การสุ่มตัวอย่าง:
เพื่อหลีกเลี่ยงการสร้างนามแฝงเมื่อลดอัตราการสุ่มตัวอย่าง ต้องปรับขนาดตัวกรองให้ตรงกับอัตราการสุ่มตัวอย่างใหม่
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
ที่ไหน:
เมื่อทำการสุ่มตัวอย่างสัญญาณจากตัวอย่าง n1 ไปเป็นตัวอย่าง n2 ตำแหน่งตัวอย่างต่อไปนี้จะถูกนำมาใช้ ดัชนี j ใช้เพื่อแสดงตัวอย่างจากสัญญาณตัวอย่าง s2(x) พจน์ (j + 0.5) เป็นจุดศูนย์กลางของกลุ่มตัวอย่างใน s2(x) ขั้นตอนจะปรับขนาดจุดใน s2(x) ไปยังจุดใน s1(x) เทอมสุดท้าย -0.5 ใน x คือการเปลี่ยนเฟสซึ่งทำให้ตัวอย่างสัมประสิทธิ์ Lanczos ถูกชดเชย
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
เมื่อทำการประมาณค่า Lanczos จะต้องได้รับการดูแลเป็นพิเศษที่ขอบเขตสัญญาณ เทคนิคการจัดการขอบทั่วไป ได้แก่:
ช่องว่างภายในเป็นศูนย์:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
การหนีบ:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
มักนิยมใช้การจับยึดเนื่องจากจะช่วยลดปัญหาขอบที่เกิดจากความไม่ต่อเนื่องของคมใกล้ขอบ อย่างไรก็ตาม การเลือกวิธีการจัดการคมตัดขึ้นอยู่กับการใช้งานเฉพาะและผลลัพธ์ที่ต้องการ
ช่วงของ s2(x) อาจมากกว่าช่วงของ s1(x) เนื่องจากกลีบของ L(x) ตัวอย่างเช่น สัญญาณอินพุต s1(x) ที่สอดคล้องกับสีพิกเซลในช่วง [0.0,1.0] จะต้องถูกยึดให้อยู่ในช่วงเดียวกันเพื่อให้แน่ใจว่าค่าเอาต์พุตจะไม่ล้นเมื่อแปลงกลับเป็นไบต์ที่ไม่ได้ลงชื่อที่ [0,255] .
เคอร์เนล Lanczos สามารถขยายไปยังหลายมิติเพื่อทำการประมาณค่ารูปภาพหรือข้อมูลที่มีมิติสูงกว่า
เคอร์เนล Lanczos สองมิติถูกกำหนดเป็น:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
สัญญาณอินเทอร์โพเลต s2(x, y) สามารถคำนวณได้โดยใช้สูตรต่อไปนี้:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
โดยที่ w(x, y) คือปัจจัยการทำให้เป็นมาตรฐานซึ่งคำนวณโดยใช้เคอร์เนล Lanczos สองมิติ
แตกต่างจากวิธีการประมาณค่าบางวิธี เคอร์เนล Lanczos ไม่สามารถแยกออกจากกันได้ ซึ่งหมายความว่าไม่สามารถแยกตัวประกอบเป็นผลคูณของเมล็ดในมิติเดียวได้ โดยทั่วไปคุณสมบัตินี้นำไปสู่ต้นทุนการคำนวณที่สูงขึ้นเมื่อเปรียบเทียบกับเคอร์เนลที่แยกได้ เพื่อปรับปรุงประสิทธิภาพ การใช้งานบางอย่างจะประมาณเคอร์เนล Lanczos โดยดำเนินการแยกส่วนสำหรับขนาดแนวนอนและแนวตั้ง
การแก้ไขแนวนอน:
การแก้ไขแนวตั้ง:
การเป็นตัวแทนทางคณิตศาสตร์:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
โปรดทราบว่าปัจจัยการทำให้เป็นมาตรฐาน w(x) และ w(y) คำนวณโดยใช้เคอร์เนล Lanczos หนึ่งมิติ
ประเด็นสำคัญ:
ในทำนองเดียวกัน การสุ่มตัวอย่างสัญญาณซ้ำหลายๆ ครั้ง เช่นเดียวกับที่ทำโดยทั่วไปในการสร้าง mipmap พื้นผิว อาจทำให้คุณภาพของภาพลดลงเนื่องจากการสะสมของข้อผิดพลาดจากขั้นตอนการสุ่มตัวอย่างแต่ละขั้นตอน
เรียกใช้ตัวอย่างการทดสอบ lancos และใช้ gnuplot เพื่อดูว่าการสุ่มตัวอย่าง Lanczos ส่งผลต่อสัญญาณมิติเดียวแบบธรรมดาอย่างไร เมื่ออัปแซมเพิลและดาวน์แซมเพิลด้วยปัจจัย 2
make
./lanczos-test
gnuplot
> load "output.plot"
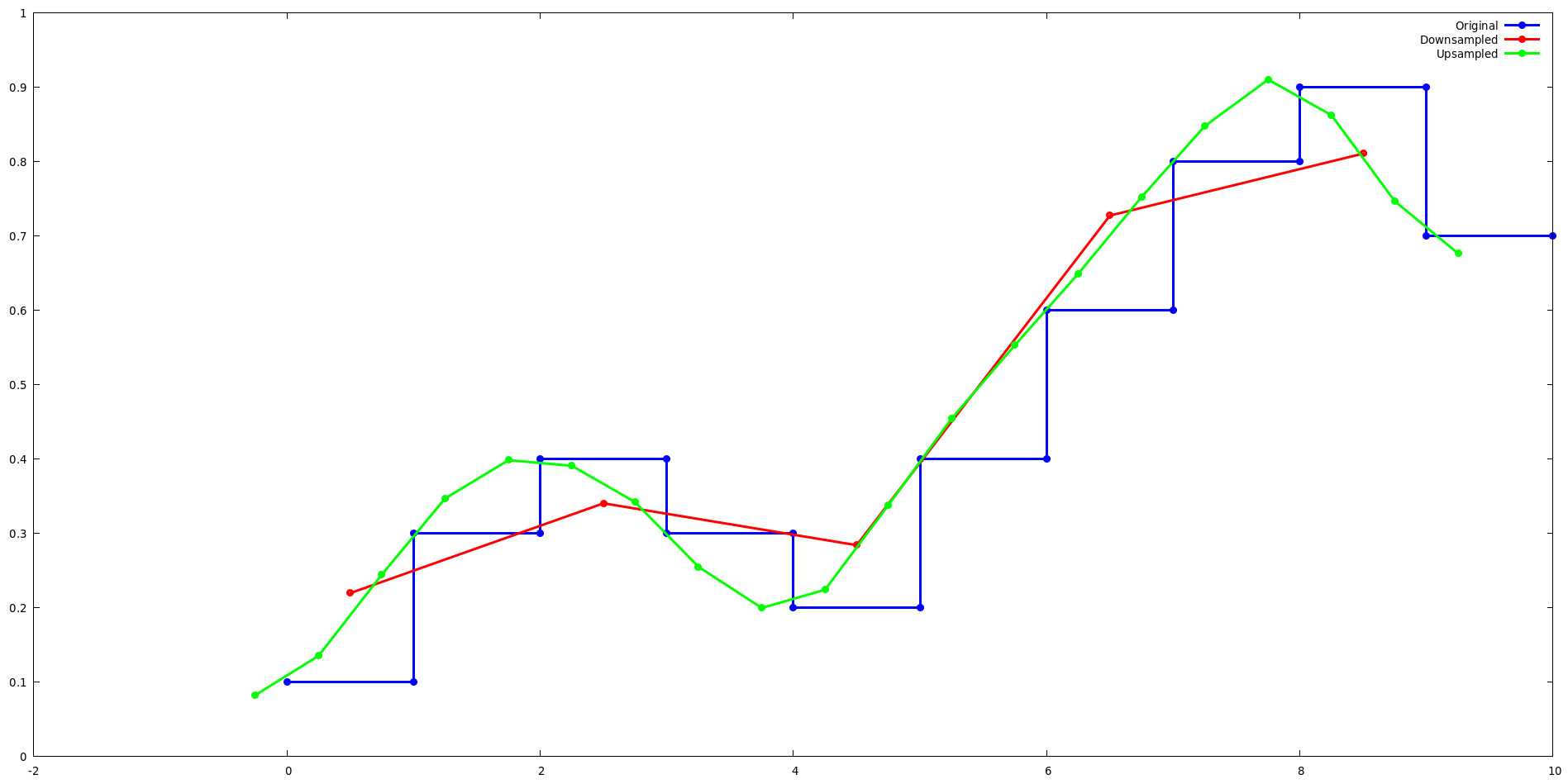
การสุ่มตัวอย่าง:
เมื่ออัปแซมปลิงด้วยกำลังสอง เคอร์เนล Lanczos จะหมุนเวียนระหว่างชุดค่าระดับ 2^ ตัวอย่างเช่น พิจารณาเอาต์พุต 4 รายการแรกของตัวอย่างอัปตัวอย่างการทดสอบ lanzcos โปรดสังเกตว่าเอาต์พุตสำหรับ L(x) ทำซ้ำสำหรับ j={0,2} และ j={1,3}
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
การสุ่มตัวอย่าง:
เมื่อดาวน์สุ่มตัวอย่างด้วยกำลังสอง เคอร์เนล Lanczos จะไม่ขึ้นอยู่กับ x เนื่องจาก (x - floor(x)) กลายเป็นค่าคงที่ซึ่งตรงกับการเปลี่ยนเฟส ตัวอย่างเช่น พิจารณาเอาต์พุต 2 รายการแรกของตัวอย่างดาวน์ตัวอย่างการทดสอบ lanzcos โปรดสังเกตว่าเอาต์พุตของ L(x) ทำซ้ำสำหรับแต่ละ j
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
เพื่อเพิ่มประสิทธิภาพเพิ่มเติม เคอร์เนล Lanczos อาจถูกคำนวณล่วงหน้าสำหรับกรณีเหล่านี้ เพื่อขจัดการคำนวณฟังก์ชัน sinc ที่มีราคาแพง
README นี้ถูกสร้างขึ้นด้วยความช่วยเหลือของ Google Gemini
ข้อมูลอ้างอิงเพิ่มเติมได้แก่:
รหัสนี้ถูกนำมาใช้โดย Jeff Boody ภายใต้ใบอนุญาต MIT
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.