ดาวน์โหลด GGS - ดาวน์โหลดซอร์สโค้ด GGS

GGS

ซอร์สโค้ดอื่น ๆ

1.0.0

ดาวน์โหลด

จีจีเอส

Greedy Gaussian Segmentation (GGS) เป็นตัวแก้ปัญหา Python สำหรับการแบ่งส่วนข้อมูลอนุกรมเวลาหลายตัวแปรอย่างมีประสิทธิภาพ สำหรับรายละเอียดการนำไปปฏิบัติ โปรดดูเอกสารของเราที่ http://stanford.edu/~boyd/papers/ggs.html

GGS Solver ใช้เมทริกซ์ข้อมูลแบบ n-by-T และแบ่งการประทับเวลา T บนเวกเตอร์ n-มิติออกเป็นส่วน ๆ ซึ่งข้อมูลได้รับการอธิบายอย่างดีในฐานะตัวอย่างอิสระจากการแจกแจงแบบเกาส์เซียนหลายตัวแปร โดยกำหนดปัญหาความเป็นไปได้สูงสุดที่ควบคุมความแปรปรวนร่วมและแก้ไขปัญหาโดยใช้ฮิวริสติกแบบละโมบ โดยมีรายละเอียดครบถ้วนตามที่อธิบายไว้ในรายงาน

ดาวน์โหลดและตั้งค่า

ดาวน์โหลดซอร์สโค้ดในเทอร์มินัลโดยเรียกใช้:

 git clone [email protected]:davidhallac/GGS.git

ยืนยันว่ารหัสถูกดาวน์โหลดอย่างถูกต้องโดยเรียกใช้:

 cd GGS
python helloworld.py

หากต้องการเขียนฟังก์ชัน Python ของคุณเองที่ใช้ ggs เพียงตรวจสอบให้แน่ใจว่า ggs.py อยู่ในไดเร็กทอรีเดียวกันกับไฟล์ใหม่ของคุณ จากนั้นเพิ่มโค้ดต่อไปนี้ที่จุดเริ่มต้นของสคริปต์:

 from ggs import *

ฟังก์ชั่นที่รองรับ

แพ็คเกจ GGS มีฟังก์ชั่นหลักสามประการ:

 bps, objectives = GGS(data, Kmax, lamb)

ค้นหาจุดพัก K ในข้อมูลสำหรับแลมบ์ดาพารามิเตอร์การทำให้เป็นมาตรฐานที่กำหนด

อินพุต

data - เมทริกซ์ข้อมูล n-by-T พร้อมการประทับเวลา T ของเวกเตอร์ n มิติ

Kmax - จำนวนเบรกพอยต์ที่จะค้นหา

lamb - พารามิเตอร์การทำให้เป็นมาตรฐานสำหรับความแปรปรวนร่วมที่ทำให้เป็นมาตรฐาน

การส่งคืน

bps - รายการของรายการ โดยที่องค์ประกอบ i ของรายการที่ใหญ่กว่าคือชุดของเบรกพอยต์ที่พบที่ K = i ในอัลกอริทึม GGS

วัตถุประสงค์ - รายการค่าวัตถุประสงค์ในแต่ละขั้นตอนระหว่างกลาง (สำหรับ K = 0 ถึง Kmax)

 meancovs = GGSMeanCov(data, breakpoints, lamb)

ค้นหาค่าเฉลี่ยและความแปรปรวนร่วมที่สม่ำเสมอของแต่ละส่วน โดยกำหนดชุดเบรกพอยท์

อินพุต

data - เมทริกซ์ข้อมูล n-by-T พร้อมการประทับเวลา T ของเวกเตอร์ n มิติ

เบรกพอยต์ - รายการตำแหน่งเบรกพอยต์

lamb - พารามิเตอร์การทำให้เป็นมาตรฐานสำหรับความแปรปรวนร่วมที่ทำให้เป็นมาตรฐาน

การส่งคืน

Meancovs - รายการสิ่งอันดับ (ค่าเฉลี่ย ความแปรปรวนร่วม) สำหรับแต่ละเซ็กเมนต์ในข้อมูล

 cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])

ดำเนินการตรวจสอบข้าม 10 เท่า และส่งคืนความน่าจะเป็นของชุดทดสอบและรถไฟสำหรับทุกๆ คู่ (K, lambda) จนถึง Kmax

อินพุต

data - เมทริกซ์ข้อมูล n-by-T พร้อมการประทับเวลา T ของเวกเตอร์ n มิติ

Kmax - จำนวนเบรกพอยต์สูงสุดที่จะเรียกใช้ GGS

lambList - รายการพารามิเตอร์การทำให้เป็นมาตรฐานที่จะทดสอบ

การส่งคืน

cvResults - รายการสิ่งอันดับ (lamb, ([TrainLL],[TestLL])) สำหรับพารามิเตอร์การทำให้เป็นมาตรฐานแต่ละรายการใน lambList ที่นี่ TrainLL และ TestLL คือความน่าจะเป็นของบันทึกต่อตัวอย่างโดยเฉลี่ยในการตรวจสอบความถูกต้องข้าม 10 เท่าสำหรับ K ทั้งหมดตั้งแต่ 0 ถึง Kmax

พารามิเตอร์เสริมเพิ่มเติม (สำหรับทั้งสามฟังก์ชันข้างต้น):

features = [] - เลือกชุดย่อยของคอลัมน์ในข้อมูลที่จะดำเนินการ

verbose = False - พิมพ์ขั้นตอนกลางเมื่อรันอัลกอริทึม

ตัวอย่างการใช้งาน

การรัน financeExample.py จะให้ผลลัพธ์ต่อไปนี้ โดยแสดงวัตถุประสงค์ (สมการที่ 4 ในรายงาน) เทียบกับจำนวนเบรกพอยท์:

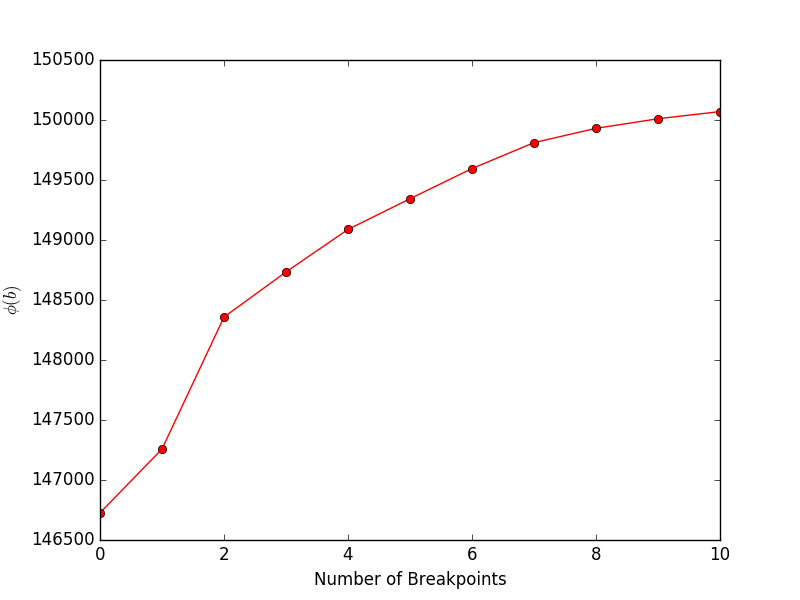
วัตถุประสงค์เทียบกับ # ของเบรกพอยต์

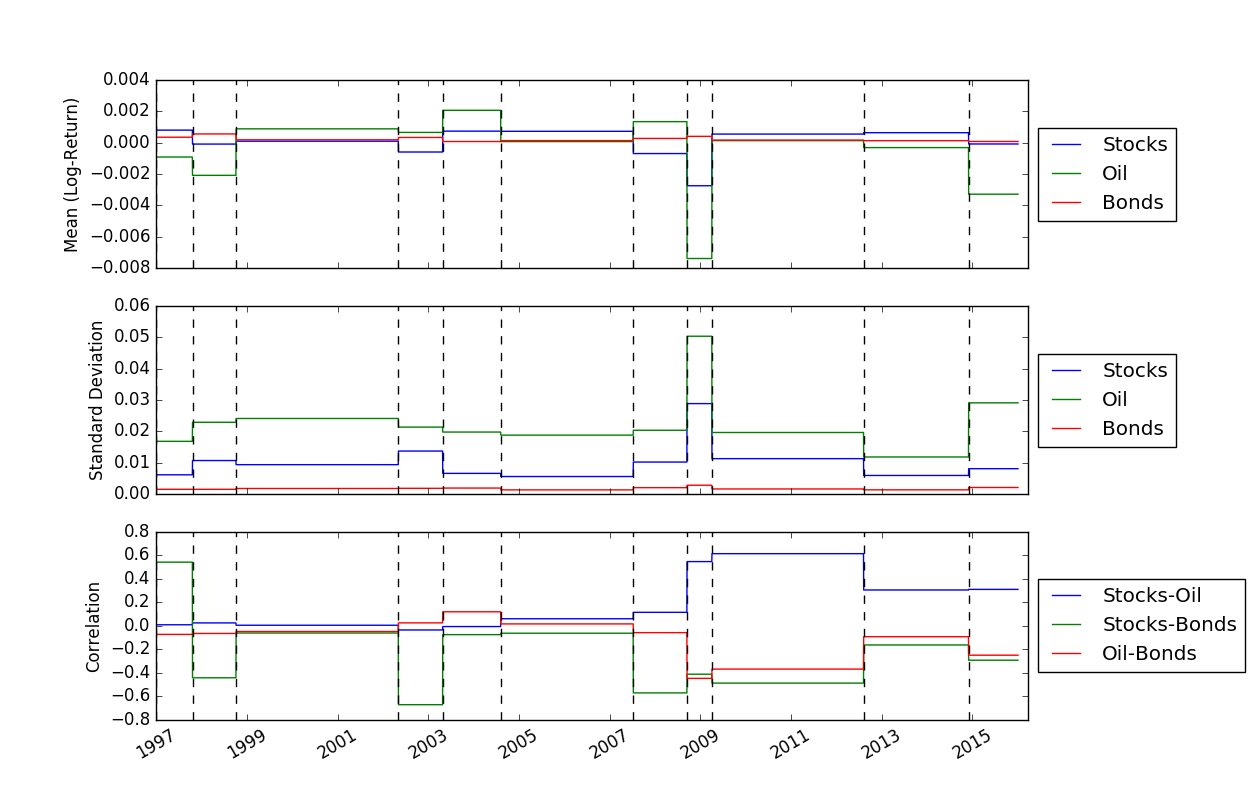
เมื่อเราแก้ไขตำแหน่งของเบรกพอยต์แล้ว เราสามารถใช้ฟังก์ชัน FindMeanCovs() เพื่อค้นหาค่าเฉลี่ยและความแปรปรวนร่วมของแต่ละส่วนได้ ในตัวอย่างใน helloworld.py การวางแผนค่าเฉลี่ย ความแปรปรวน และความแปรปรวนร่วมของสัญญาณทั้งสามจะให้ผล:

วิธีการและความแปรปรวนร่วมในช่วงเวลาหนึ่ง

ในการเรียกใช้การตรวจสอบข้ามซึ่งจะมีประโยชน์ในการกำหนดค่าที่เหมาะสมที่สุดของ K และ lambda เราสามารถใช้โค้ดต่อไปนี้เพื่อโหลดข้อมูล เรียกใช้การตรวจสอบความถูกต้องข้าม จากนั้นวางแผนการทดสอบและฝึกความน่าจะเป็น:

 from ggs import *
import numpy as np
import matplotlib.pyplot as plt

filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]

#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)

trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()

โครงเรื่องที่ได้จะมีลักษณะดังนี้:

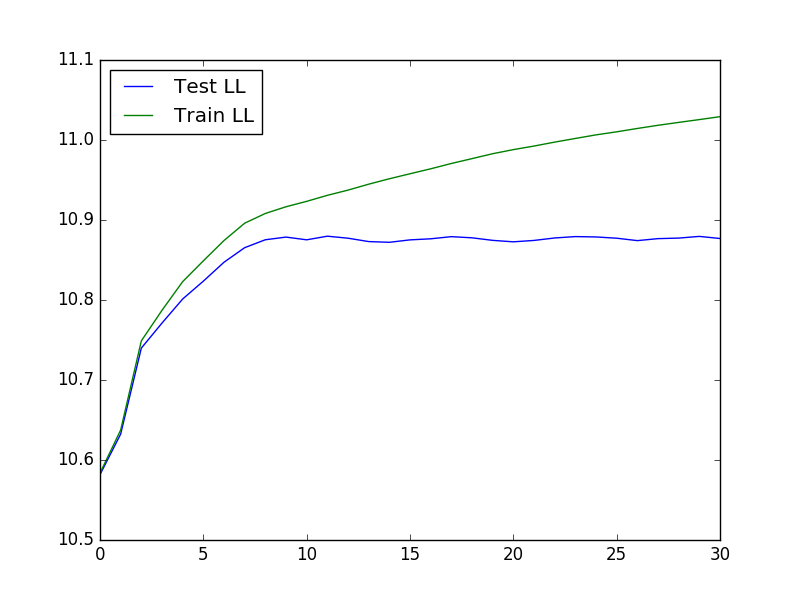
ทดสอบและฝึกความน่าจะเป็น