greta.gam: โมเดลการบวกทั่วไปใน greta โดยใช้ mgcv

greta.gam ช่วยให้คุณใช้ฟังก์ชันที่ราบรื่นยิ่งขึ้นและไวยากรณ์ของสูตรของ mgcv เพื่อกำหนดคำศัพท์ที่ราบรื่นสำหรับใช้ในแบบจำลอง greta จากนั้น คุณสามารถกำหนดความเป็นไปได้ของคุณเองในการสร้างแบบจำลองให้เสร็จสิ้น และปรับให้เหมาะสมโดย MCMC

นี่คืองานระหว่างดำเนินการ!

ตัวอย่าง

ต่อไปนี้คือตัวอย่างง่ายๆ ที่ดัดแปลงมาจากไฟล์วิธีใช้ mgcv ?gam :

ใน mgcv :

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

ตอนนี้ติดตั้งโมเดลเดียวกันใน greta :

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )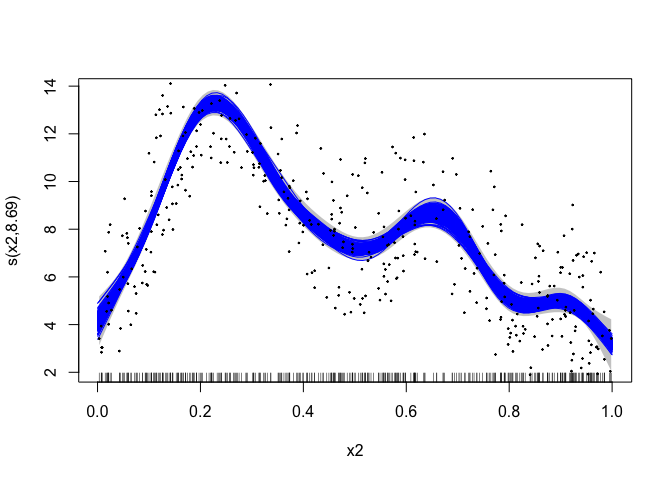

รายละเอียดทางเทคนิคโดยย่อ

greta.gam ใช้กลเม็ดเล็กๆ น้อยๆ จากรูทีน jagam (Wood, 2016) ใน mgcv เพื่อให้สิ่งต่าง ๆ ทำงานได้ นี่คือรายละเอียดโดยย่อสำหรับผู้ที่สนใจงานภายใน...

การตีความแบบเบย์ของ GAM

GAM เป็นโมเดลที่มีการตีความแบบเบย์ (แม้ว่าจะติดตั้งโดยใช้วิธี "ผู้บ่อยครั้ง") เราสามารถนึกถึงเมทริกซ์การลงโทษที่นุ่มนวลกว่าในฐานะเมทริกซ์ความแม่นยำก่อนหน้าในแบบจำลองเอฟเฟกต์สุ่มแบบเบย์ เมทริกซ์การออกแบบถูกสร้างขึ้นทุกประการเหมือนกับในกรณีที่ใช้บ่อย ดู Miller (2021) สำหรับข้อมูลพื้นฐานเพิ่มเติมเกี่ยวกับเรื่องนี้

เมทริกซ์การลงโทษ

มีความยากลำบากเล็กน้อยในการตีความ GAM แบบเบย์ ในรูปแบบที่ไร้เดียงสา นักบวชนั้นไม่เหมาะสมเนื่องจากเป็นโมฆะของการลงโทษ (ในกรณี 1D โดยปกติจะเป็นคำเชิงเส้น) เพื่อให้ได้นักบวชที่เหมาะสม เราสามารถใช้หนึ่งใน “กลเม็ด” ที่ใช้ใน Marra & Wood (2011) นั่นคือการลงโทษส่วนของบทลงโทษที่นำไปสู่การกระทำที่ไม่เหมาะสมก่อนหน้านี้ เราใช้ตัวเลือกที่ได้รับจาก jagam และสร้างเมทริกซ์การลงโทษเพิ่มเติมสำหรับเงื่อนไขเหล่านี้ (จากการสลายตัวแบบไอเกนของเมทริกซ์การลงโทษ; ดู Marra & Wood, 2011)