หน้าแรก | การติดตั้ง | เอกสารประกอบ | บทช่วยสอน | นักพัฒนา
rodeo เป็นไลบรารี Python ที่รวดเร็วซึ่งใช้ตัวเลขความน่าจะเป็นในการแก้สมการเชิงอนุพันธ์สามัญ (ODE) นั่นคือ ตัวแก้ปัญหา ODE ส่วนใหญ่ (เช่น วิธีของออยเลอร์) จะสร้างการประมาณค่าที่กำหนดให้กับ ODE บนตารางขนาดขั้นตอน
rodeo ให้การประมาณแบบน้ำหนักเบาและขยายได้สำหรับกระบวนทัศน์การกรองแบบเบย์แบบไม่เชิงเส้นซึ่งพบได้ทั่วไปในนักแก้ปัญหาที่น่าจะเป็นจำนวนมาก (Tronarp et al (2018)) สิ่งนี้เริ่มต้นด้วยการวางกระบวนการแบบเกาส์เซียนไว้ก่อนหน้าโซลูชัน ODE และอัปเดตตามลำดับเมื่อตัวแก้ปัญหาก้าวผ่านกริด rodeo สร้างขึ้นบน jax ซึ่งช่วยให้สามารถรวบรวมและแยกความแตกต่างได้โดยอัตโนมัติ API ของ jax เกือบจะเทียบเท่ากับของ numpy
rodeo มีเครื่องมือหลักสองอย่าง เครื่องมือหนึ่งสำหรับการประมาณโซลูชัน ODE และอีกเครื่องมือหนึ่งสำหรับการอนุมานพารามิเตอร์ สำหรับแบบแรกเราจัดเตรียมไว้ให้:
solve : การใช้ตัวแก้ปัญหา ODE ที่น่าจะเป็นซึ่งใช้กระบวนทัศน์การกรองแบบเบย์แบบไม่เชิงเส้นสำหรับอย่างหลัง เรามีวิธีการประมาณความน่าจะเป็น:
basic : การใช้วิธีการประมาณความน่าจะเป็นขั้นพื้นฐาน (รายละเอียดสามารถพบได้ใน Wu และ Lysy (2023))fenrir : การปรับใช้ Fenrir (Tronarp et al (2022))marginal_mcmc : การใช้ MCMC ของวิธีการของ Chkrebtii (Chkrebtii et al (2016))dalton : การใช้การประมาณค่าความน่าจะเป็นของ ODE ที่ปรับเปลี่ยนข้อมูลได้ (Wu และ Lysy (2023))ตัวอย่างโดยละเอียดสำหรับการใช้งานสามารถดูได้ในส่วนเอกสารประกอบ โปรดทราบว่านี่เป็นเวอร์ชัน jax -only ของ rodeo สำหรับเวอร์ชันเก่าที่ใช้แบ็กเอนด์อื่นๆ โปรดดูที่นี่
ดาวน์โหลด repo จาก GitHub จากนั้นติดตั้งด้วยสคริปต์ setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . ก่อนอื่น โปรดไปที่ readthedocs เพื่อดูเอกสารประกอบที่แสดงผลสำหรับตัวอย่างต่อไปนี้
บทช่วยสอนแบบเริ่มต้นอย่างรวดเร็วเกี่ยวกับการแก้ปัญหา ODE แบบง่ายๆ
ตัวอย่างการแก้ ODE ที่มีลำดับสูงกว่า
ตัวอย่างการแก้ปัญหา ODE ที่วุ่นวายอย่างยากลำบาก
ตัวอย่างของปัญหาการอนุมานพารามิเตอร์ที่เราใช้การประมาณลาปลาซ
ในการฝึกปฏิบัตินี้ เราจะแสดงทั้งวิธีแก้ปัญหา ODE ด้วยตัวแก้ปัญหาความน่าจะเป็นและการอนุมานพารามิเตอร์ ก่อนอื่นเราจะอธิบายการตั้งค่าสำหรับการแก้ไข ODE ด้วยเหตุนี้ ลองพิจารณาตัวอย่าง ODE ที่เรียงลำดับแรกต่อไปนี้ (โมเดล FitzHugh-Nagumo )
ทางออกอยู่ที่ไหน
ตามสัญกรณ์ของ (Wu และ Lysy (2023)) เรามี
สำหรับ
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) เราเปรียบเทียบโซลูชันจากตัวแก้ปัญหากับโซลูชันที่กำหนดโดย odeint ในไลบรารี scipy
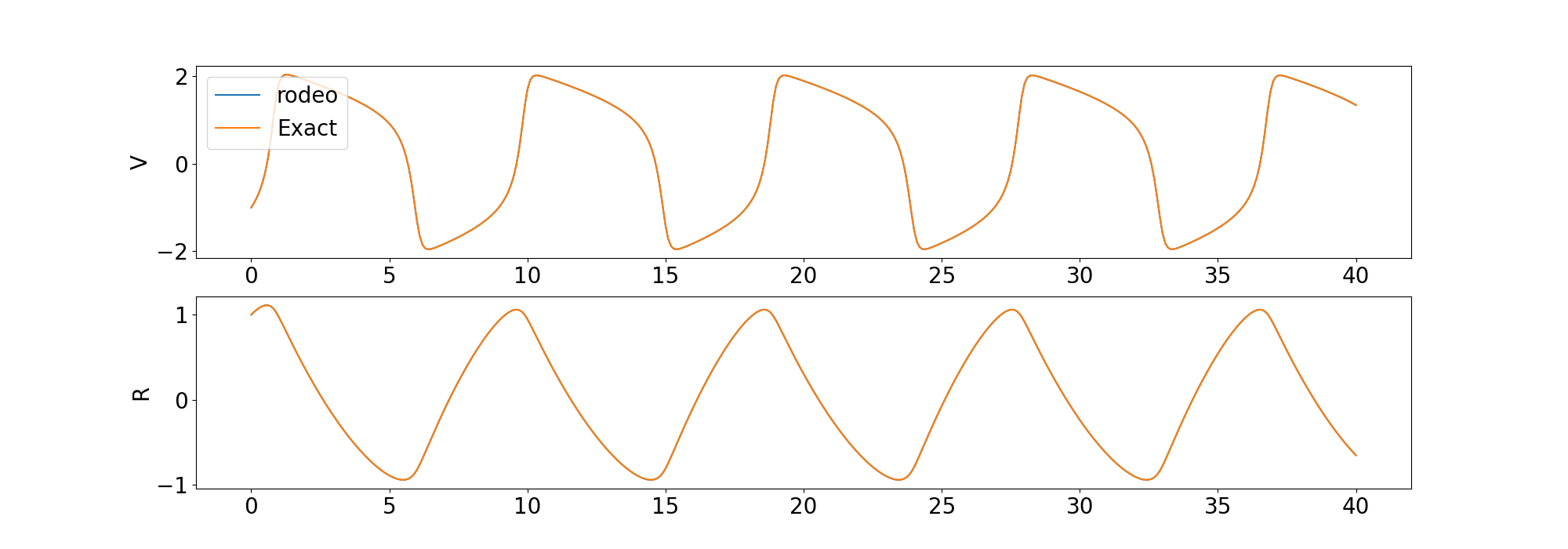
นอกจากนี้เรายังรวมตัวอย่างสำหรับการแก้ไข ODE ที่มีลำดับสูงกว่าและ ODE ที่วุ่นวายอีกด้วย
ตอนนี้เราย้ายไปที่ปัญหาการอนุมานพารามิเตอร์ rodeo มีวิธีประมาณความน่าจะเป็นหลายวิธีซึ่งสรุปไว้ในส่วนคำอธิบาย ในที่นี้ เราจะใช้วิธีการประมาณความน่าจะเป็น basic สมมติว่าการสังเกตถูกจำลองผ่านแบบจำลอง
ที่ไหน basic ได้
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) นี่เป็นตัวอย่างพื้นฐานในการสาธิตการใช้งาน เราขอแนะนำการประมาณความน่าจะเป็นที่ซับซ้อนมากขึ้น ซึ่งเผยแพร่ความไม่แน่นอนของการแก้ปัญหาไปสู่การประมาณความน่าจะเป็น เช่น fenrir , marginal_mcmc และ dalton โปรดดูบทช่วยสอนการอนุมานพารามิเตอร์สำหรับรายละเอียดเพิ่มเติม
ต่อไปนี้เป็นผลลัพธ์บางส่วนที่เกิดจากการประมาณความน่าจะเป็นต่างๆ ที่พบใน rodeo จาก /examples/ :
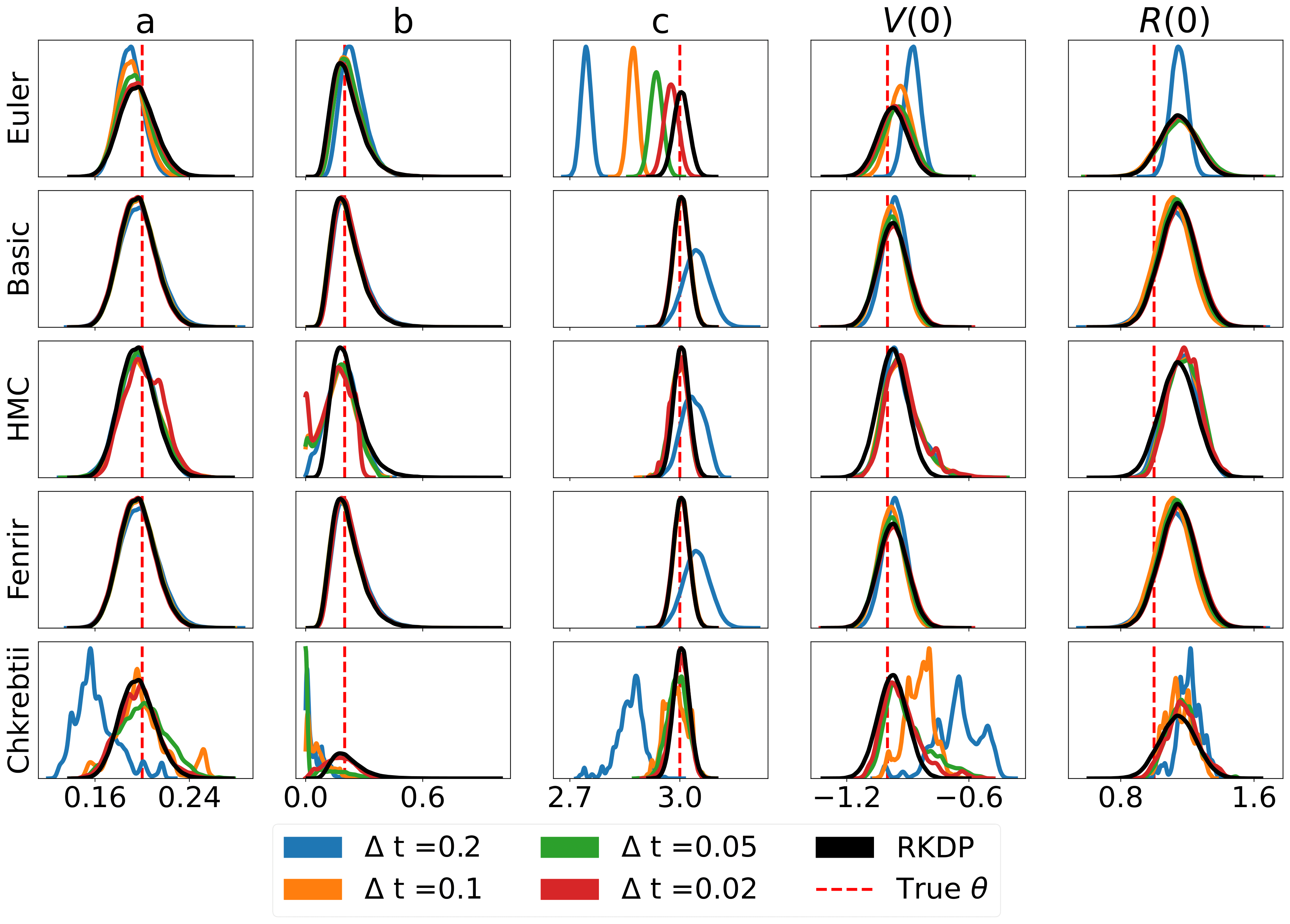
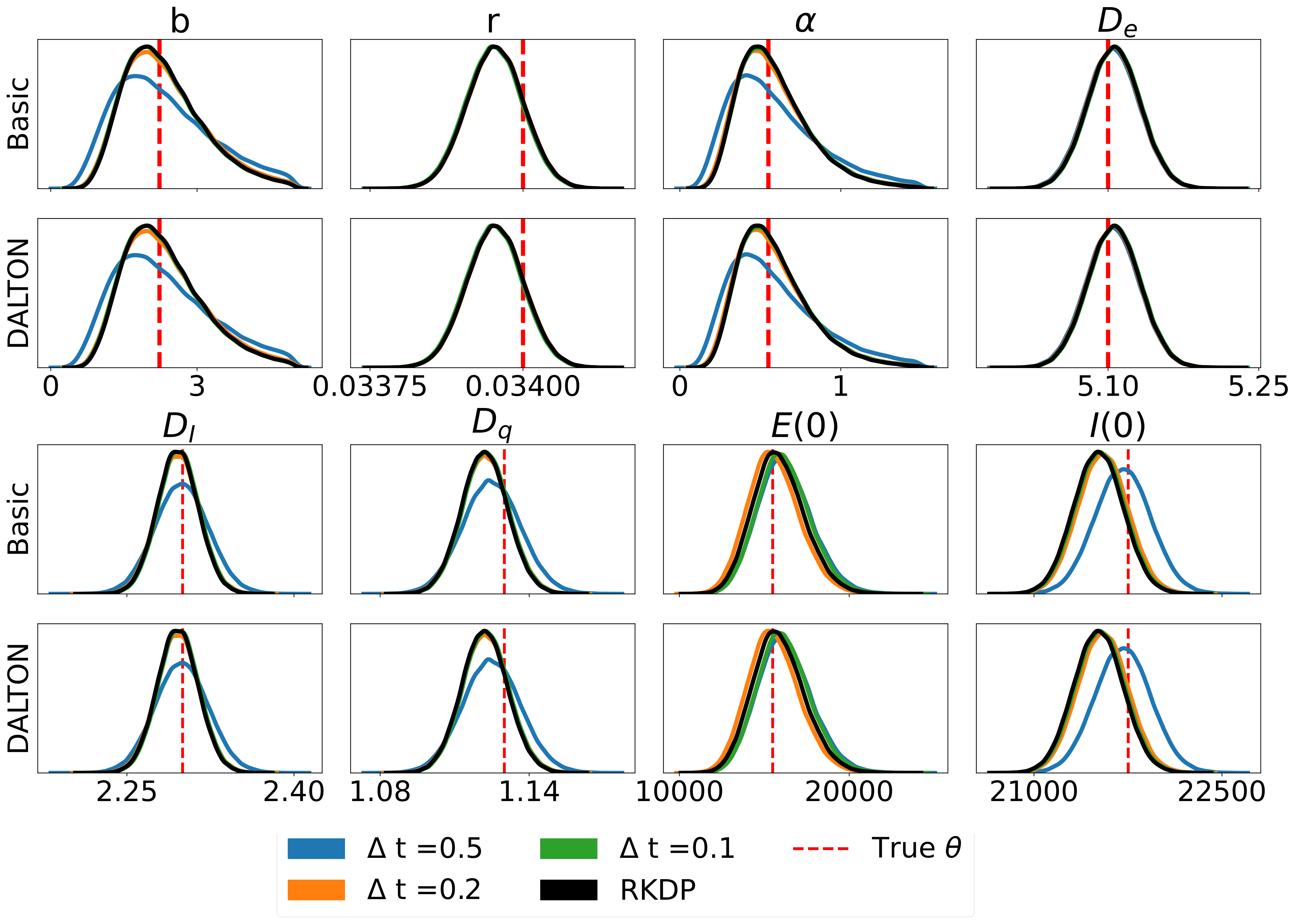
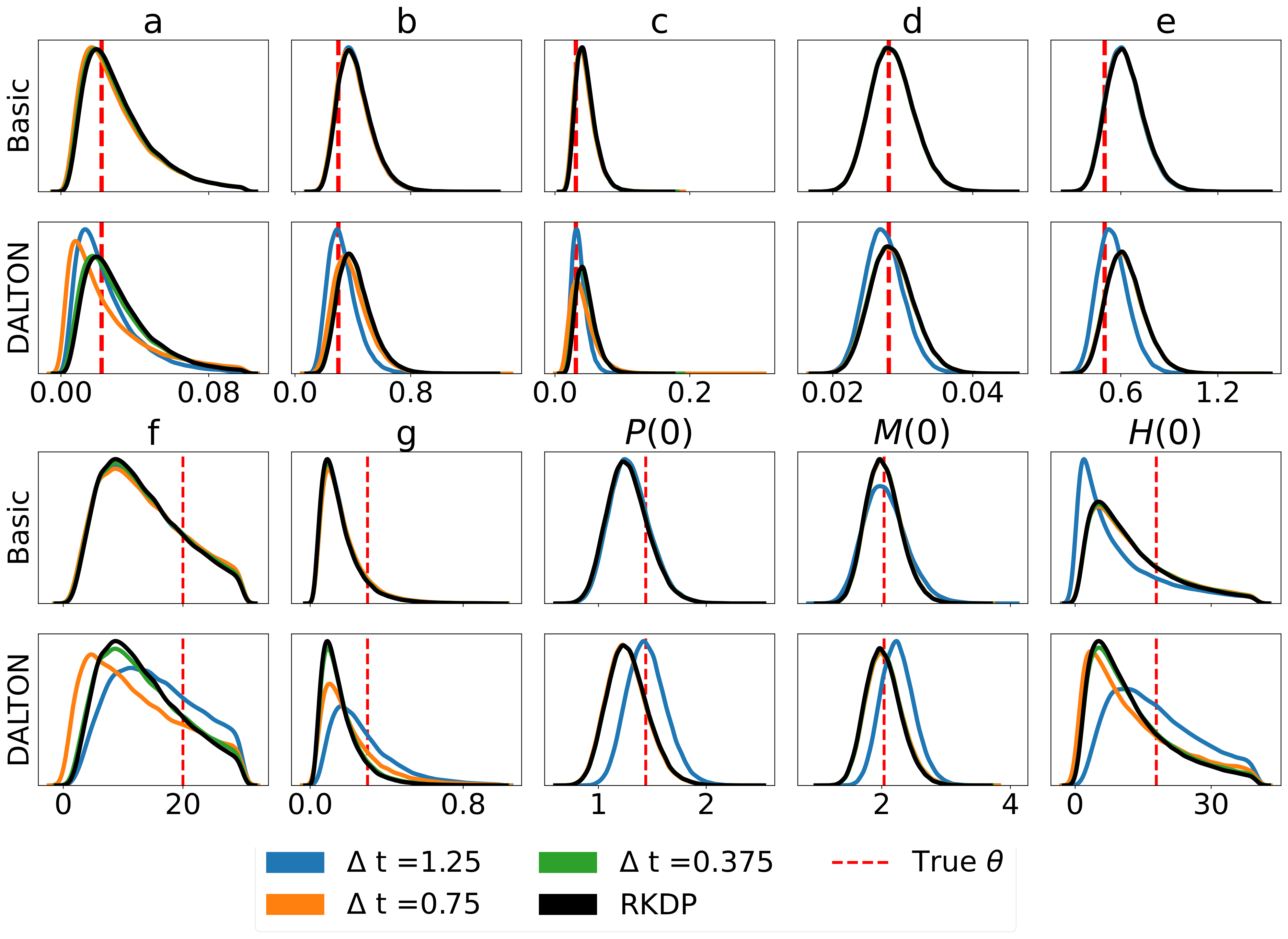
การทดสอบหน่วยสามารถรันผ่านคำสั่งต่อไปนี้:
cd tests
python -m unittest discover -v หรือติดตั้ง tox จากนั้นจากภายใน rodeo ให้ป้อนบรรทัดคำสั่ง: tox
เอกสาร HTML สามารถรวบรวมได้จากโฟลเดอร์รูท:
pip install .[docs]
cd docs
make html สิ่งนี้จะสร้างเอกสารประกอบใน docs/build