@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}คุณรู้หรือไม่ว่า neurodiffeq รองรับชุดโซลูชันและสามารถใช้เพื่อแก้ไขปัญหาแบบย้อนกลับได้ ดูที่นี่!
- คุ้นเคยกับ neurodiffeq แล้วหรือยัง? - ข้ามไปที่คำถามที่พบบ่อย
neurodiffeq เป็นแพ็คเกจสำหรับการแก้สมการเชิงอนุพันธ์ด้วยโครงข่ายประสาทเทียม สมการเชิงอนุพันธ์คือสมการที่เกี่ยวข้องกับฟังก์ชันบางอย่างกับอนุพันธ์ของมัน พวกมันปรากฏในขอบเขตทางวิทยาศาสตร์และวิศวกรรมศาสตร์ที่หลากหลาย โดยทั่วไปปัญหาเหล่านี้สามารถแก้ไขได้ด้วยวิธีตัวเลข (เช่น ผลต่างอันจำกัด องค์ประกอบจำกัด) แม้ว่าวิธีการเหล่านี้จะมีประสิทธิภาพและเพียงพอ แต่ความสามารถในการแสดงออกนั้นถูกจำกัดด้วยการแสดงฟังก์ชัน คงจะน่าสนใจถ้าเราสามารถคำนวณคำตอบของสมการเชิงอนุพันธ์ที่มีความต่อเนื่องและหาอนุพันธ์ได้
ในฐานะตัวประมาณฟังก์ชันสากล โครงข่ายประสาทเทียมได้รับการแสดงให้เห็นว่ามีศักยภาพในการแก้สมการเชิงอนุพันธ์สามัญ (ODE) และสมการเชิงอนุพันธ์ย่อย (PDE) ด้วยเงื่อนไขเริ่มต้น/ขอบเขตที่แน่นอน จุดมุ่งหมายของ neurodiffeq คือการใช้เทคนิคที่มีอยู่ของการใช้ ANN เพื่อแก้สมการเชิงอนุพันธ์ในลักษณะที่ช่วยให้ซอฟต์แวร์มีความยืดหยุ่นเพียงพอที่จะทำงานกับปัญหาต่างๆ ที่ผู้ใช้กำหนด
เช่นเดียวกับไลบรารีมาตรฐานส่วนใหญ่ neurodiffeq โฮสต์บน PyPI หากต้องการติดตั้งเวอร์ชันเสถียรล่าสุด
pip install -U neurodiffeq # '-U' หมายถึงการอัปเดตเป็นเวอร์ชันล่าสุด
หรือคุณสามารถติดตั้งไลบรารีด้วยตนเองเพื่อเข้าถึงคุณสมบัติใหม่ของเราก่อนใคร นี่เป็นวิธีที่แนะนำสำหรับนักพัฒนาที่ต้องการสนับสนุนห้องสมุด
git clone https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip ติดตั้ง -r ข้อกำหนด การติดตั้ง pip # หากต้องการเปลี่ยนแปลงไลบรารี ให้ใช้ `pip install -e .`pytest tests/ # รันการทดสอบ ไม่จำเป็น.
เรายินดีที่จะช่วยเหลือคุณในทุกคำถาม ในระหว่างนี้ คุณสามารถตรวจสอบคำถามที่พบบ่อยได้
หากต้องการดูบทช่วยสอนและเอกสารประกอบของ neurodiffeq โปรดตรวจสอบเอกสารอย่างเป็นทางการ
นอกเหนือจากเอกสารประกอบแล้ว เมื่อเร็วๆ นี้เราได้จัดทำวิดีโอสาธิตการใช้งานแบบสั้นๆ พร้อมสไลด์
จากการนำเข้า neurodiffeq แตกต่างจาก neurodiffeq.solvers นำเข้า Solver1D, Solver2D จาก neurodiffeq.conditions นำเข้า IVP, DirichletBVP2D จาก neurodiffeq.networks นำเข้า FCNN, SinActv
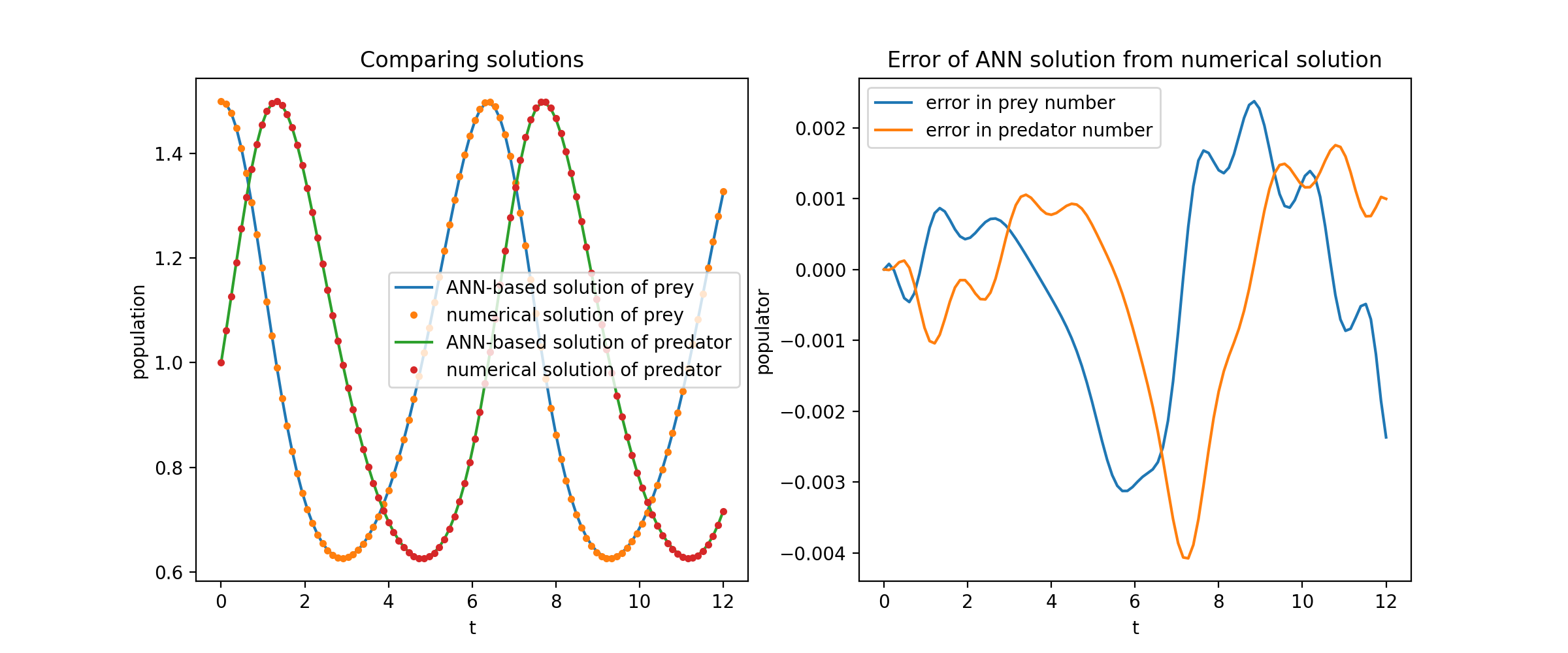
ที่นี่เราจะแก้ระบบไม่เชิงเส้นของ ODE สองตัวที่เรียกว่าสมการ Lotka–Volterra มีฟังก์ชันที่ไม่รู้จักสองฟังก์ชัน ( u และ v ) และตัวแปรอิสระตัวเดียว ( t )
def ode_system(u, v, t): กลับ [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]เงื่อนไข = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]ตัวแก้ปัญหา = Solver1D(ode_system, เงื่อนไข, t_min=0.1, t_max=12.0, nets=nets)solver.fit(max_epochs=3000)solution = solver.get_solution()
solution เป็นวัตถุที่สามารถเรียกได้ คุณสามารถส่งผ่านอาร์เรย์จำนวนมากหรือเทนเซอร์คบเพลิงได้
u, v = วิธีแก้ปัญหา (t, to_numpy=True) # t สามารถเป็น np.ndarray หรือ torch.Tensor
การวางแผน u และ v เทียบกับโซลูชันการวิเคราะห์ของพวกเขาให้ผลลัพธ์ดังนี้:
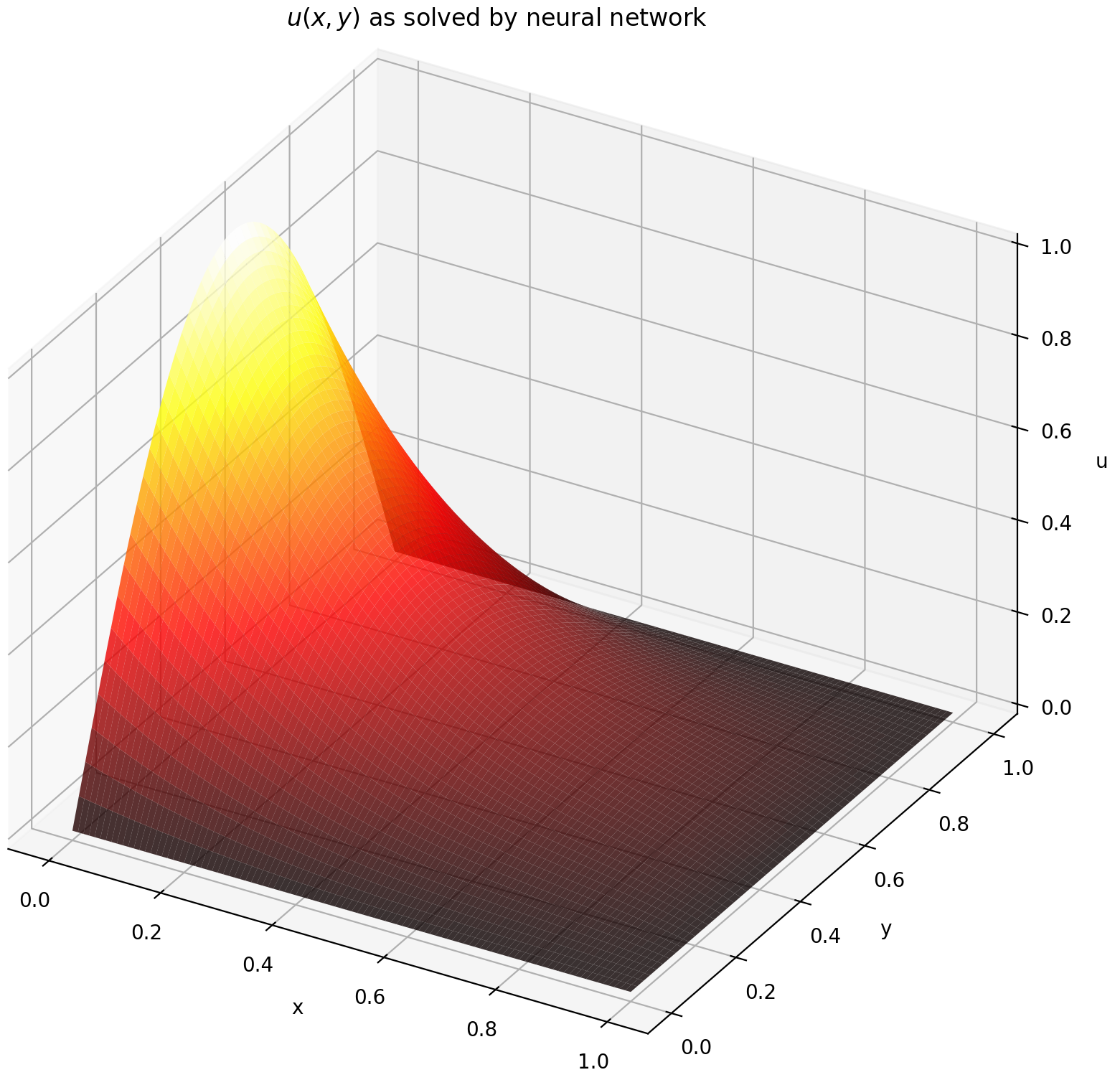
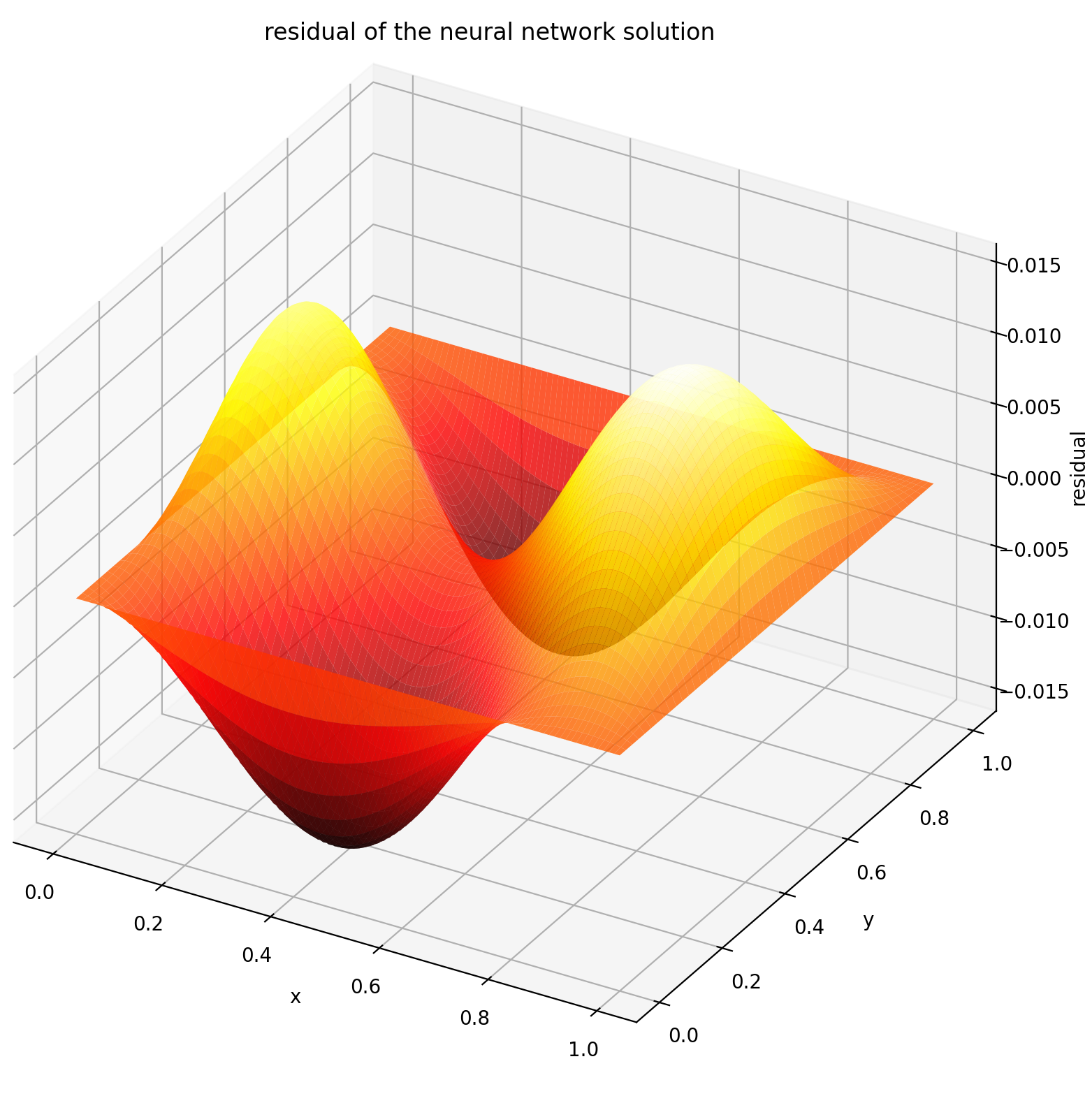
ที่นี่เราจะแก้สมการลาปลาซกับเงื่อนไขขอบเขตดิริชเลต์บนสี่เหลี่ยมมุมฉาก โปรดทราบว่าเราเลือกสมการลาปลาซเนื่องจากความเรียบง่ายของโซลูชันการวิเคราะห์ทางคอมพิวเตอร์ ในทางปฏิบัติ คุณสามารถลองใช้ PDE ที่ไม่เชิงเส้นและวุ่นวายใดๆ ได้ หากคุณปรับแต่งตัวแก้ปัญหาได้ดีเพียงพอ
การแก้ปัญหาระบบ 2-D PDE ค่อนข้างคล้ายกับการแก้ปัญหา ODE ยกเว้นว่ามีตัวแปร สอง ตัวคือ x และ y สำหรับปัญหาค่าขอบเขต หรือ x และ t สำหรับปัญหาค่าขอบเขตเริ่มต้น ซึ่งทั้งสองค่าได้รับการสนับสนุน
def pde_system(u, x, y): return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: torch. บาป(np.pi*y),x_max=1, x_max_val=แลมบ์ดา y: 0, y_min=0, y_min_val=แลมบ์ดา x: 0, y_max=1, y_max_val=แลมบ์ดา x: 0,
-
]nets = [FCNN(n_input_units=2, n_output_units=1, Hidden_units=(512,))]solver = Solver2D(pde_system, เงื่อนไข, xy_min=(0, 0), xy_max=(1, 1), nets=nets) Solver.fit(max_epochs=2000)โซลูชั่น = Solver.get_solution() ลักษณะเฉพาะของ solution สำหรับ 2D PDE นั้นแตกต่างจาก ODE เล็กน้อย ขอย้ำอีกครั้งว่ามันใช้อาร์เรย์จำนวนมากหรือเทนเซอร์คบเพลิง
u = วิธีแก้ปัญหา (x, y, to_numpy=True)
การประเมินคุณใน [0,1] × [0,1] จะได้ผลลัพธ์ดังต่อไปนี้
| โซลูชันที่ใช้ ANN | ส่วนที่เหลือของ PDE |
|---|---|
 |  |
จอภาพเป็นเครื่องมือสำหรับการแสดงภาพโซลูชัน PDE/ODE รวมถึงประวัติการสูญเสียและตัววัดแบบกำหนดเองระหว่างการฝึกอบรม ผู้ใช้ Jupyter Notebooks จำเป็นต้องเรียกใช้เวทมนตร์ %matplotlib notebook สำหรับผู้ใช้ Jupyter Lab ให้ลองใช้ %matplotlib widget
จาก neurodiffeq.monitors นำเข้า Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
คุณควรเห็นพล็อตอัปเดต ทุก ๆ 100 ยุค รวมถึง ยุคสุดท้าย โดยแสดงสองพล็อต - แผนหนึ่งสำหรับการแสดงภาพโซลูชันในช่วงเวลา [0,12] และอีกแผนสำหรับประวัติการสูญเสีย (การฝึกอบรมและการตรวจสอบ)
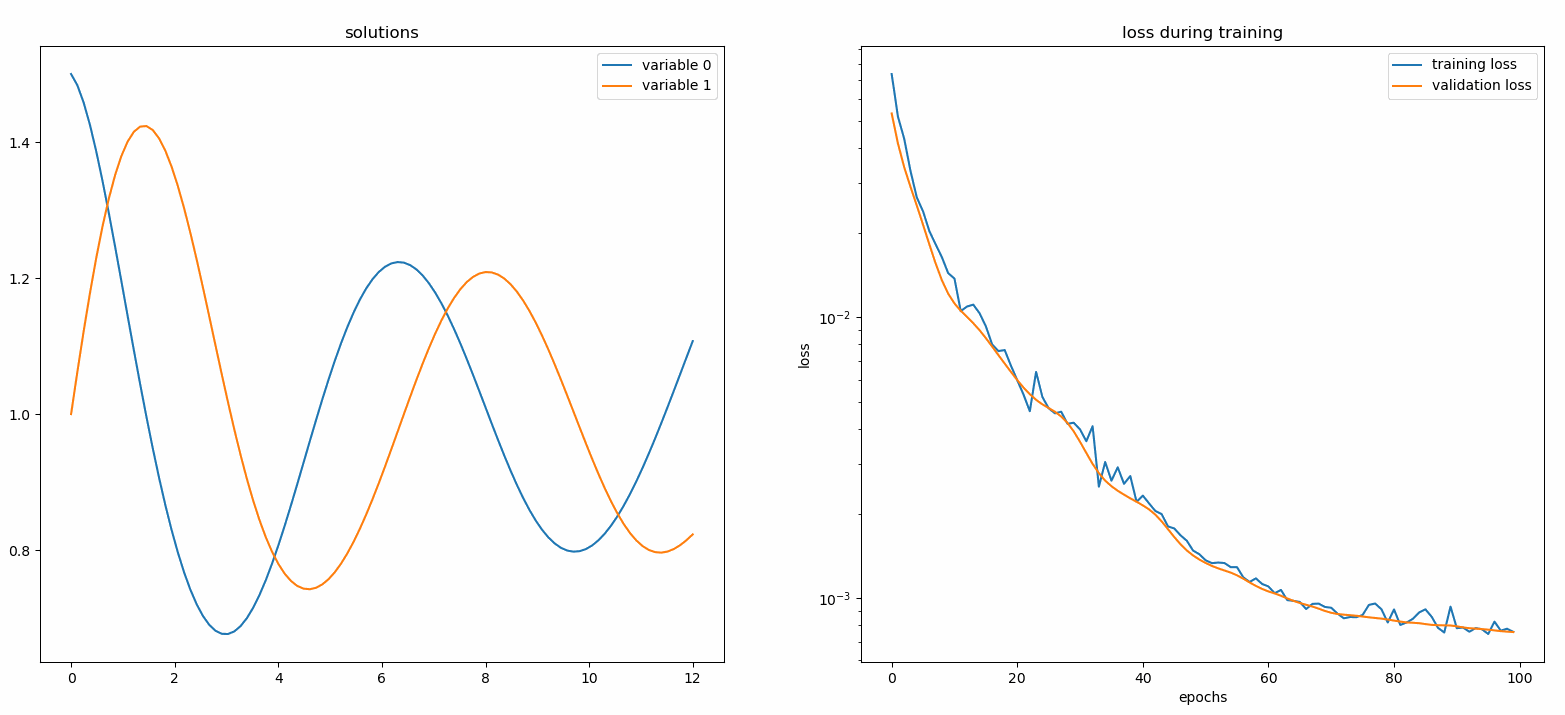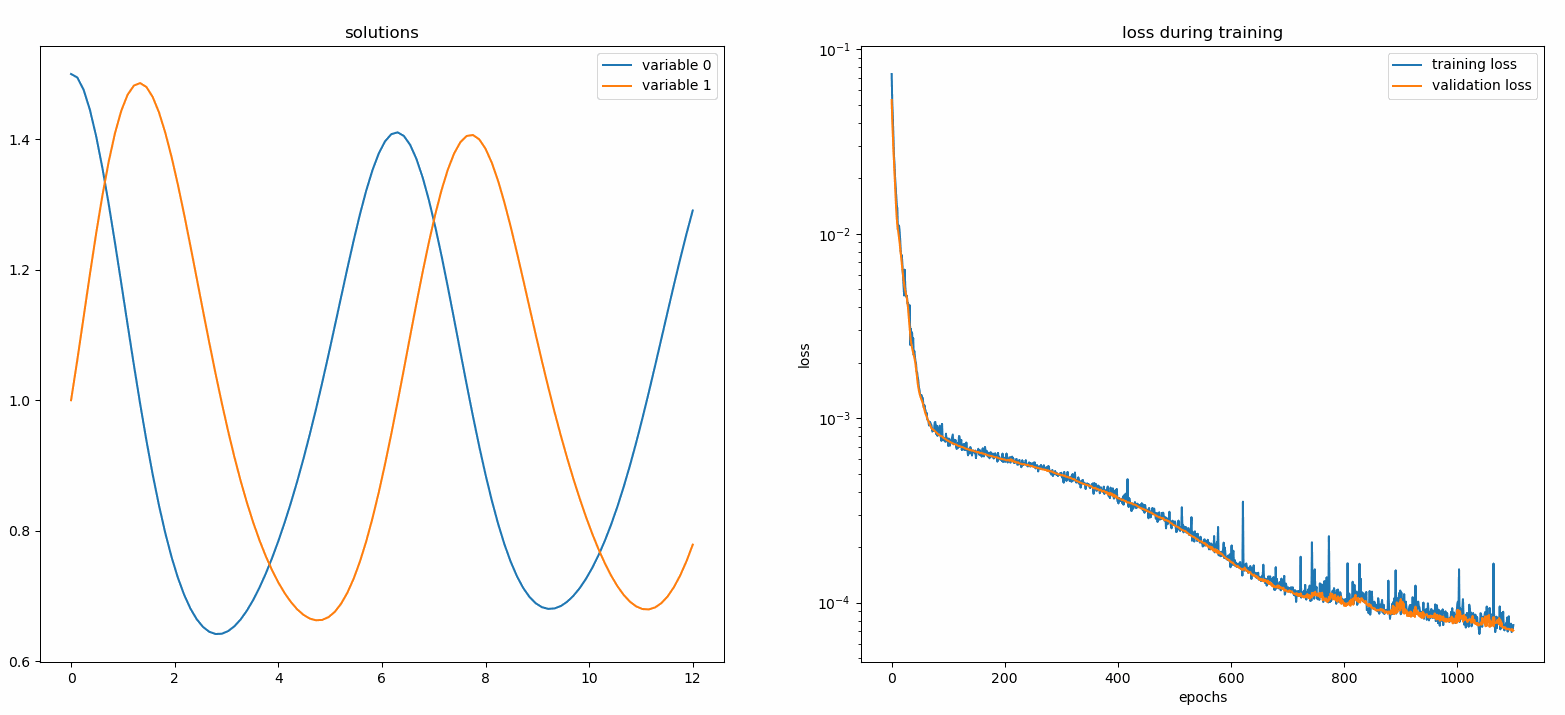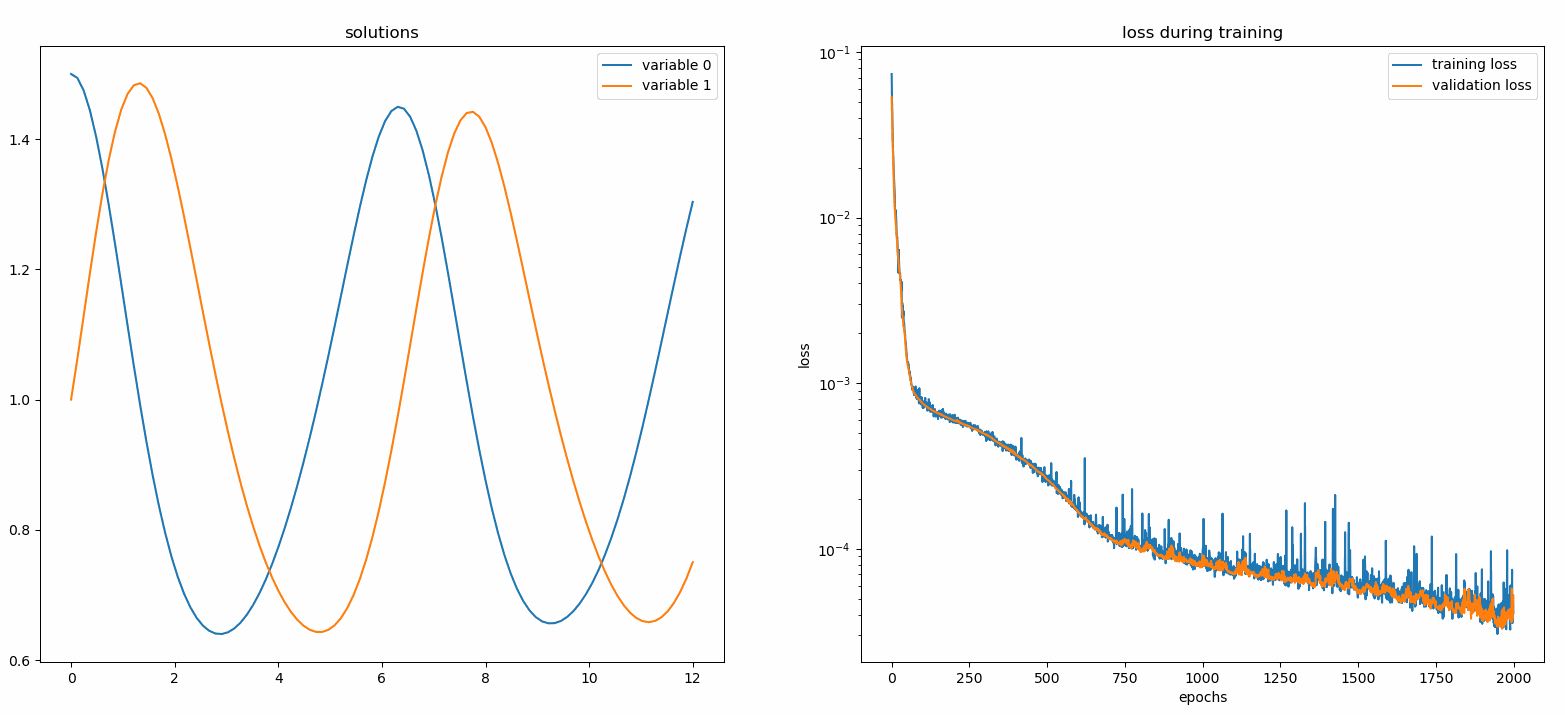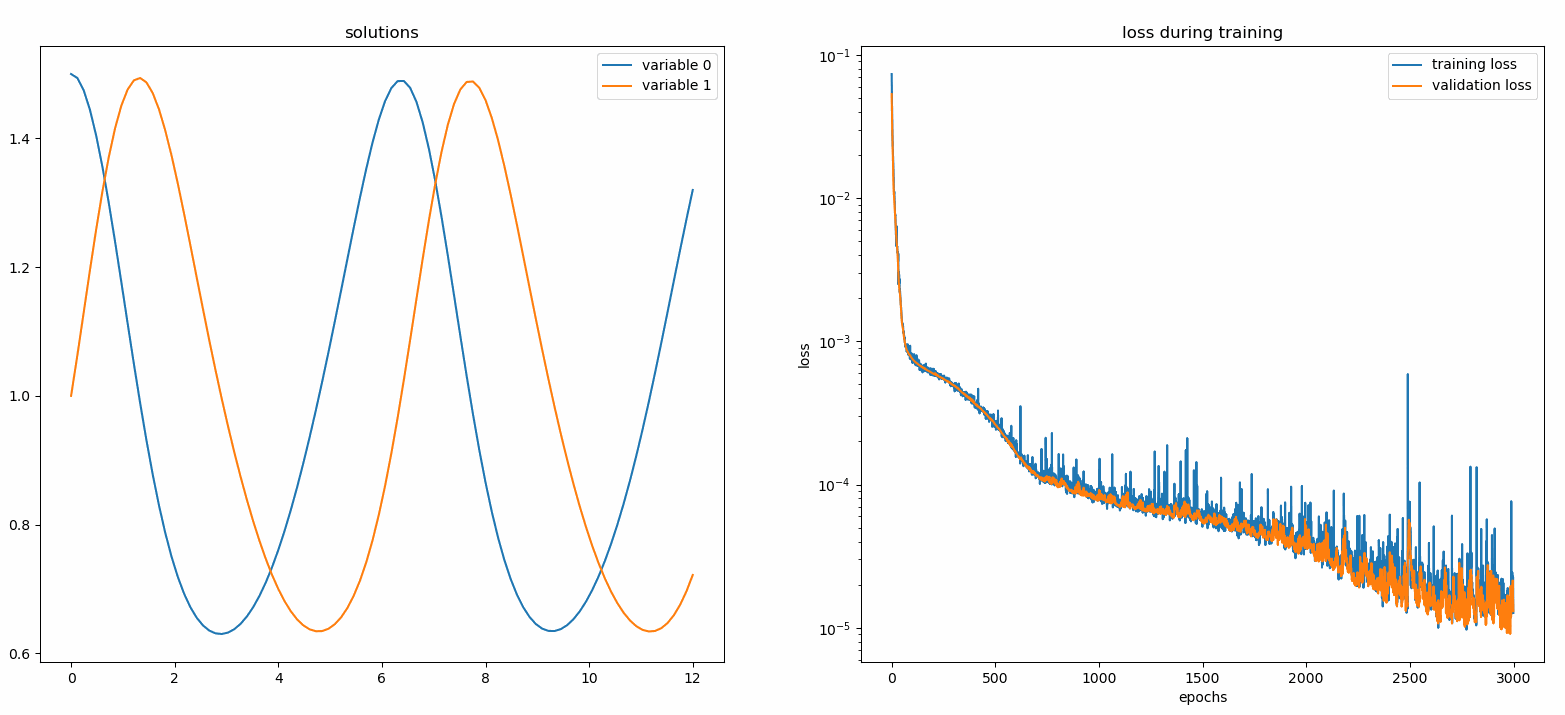
เพื่อความสะดวก เราได้ใช้ FCNN ซึ่งเป็นโครงข่ายประสาทเทียมที่เชื่อมต่อโดยสมบูรณ์ ซึ่งสามารถปรับแต่งหน่วยที่ซ่อนอยู่และฟังก์ชันการเปิดใช้งานได้
จาก neurodiffeq.networks นำเข้า FCNN# ค่าเริ่มต้น: n_input_units=1, n_output_units=1, Hidden_units=[32, 32], activation=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., Hidden_units=[ ..., ..., ...], การเปิดใช้งาน=...) ...อวน = [net1, net2, ...]
โดยปกติแล้ว FCNN จะเป็นจุดเริ่มต้นที่ดี สำหรับผู้ใช้ขั้นสูง ตัวแก้ปัญหาสามารถทำงานร่วมกับ torch.nn.Module แบบกำหนดเองใดๆ ได้ ข้อจำกัดเพียงอย่างเดียวคือ:
โมดูลใช้เทนเซอร์ของรูปร่าง (None, n_coords) และเอาท์พุตเทนเซอร์ของรูปร่าง (None, 1)
จะต้องมีโมดูล n_funcs ทั้งหมดใน nets ที่จะส่งผ่านไปยัง solver = Solver(..., nets=nets)
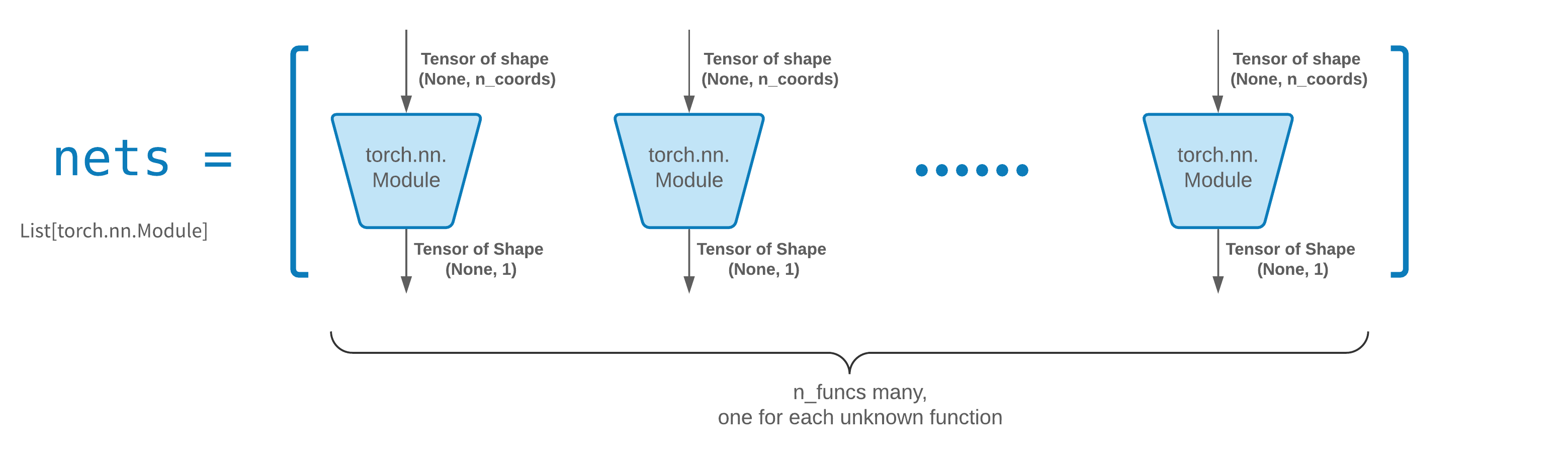
จริงๆ แล้ว neurodiffeq มีฟีเจอร์ single_net ที่ไม่เป็นไปตามกฎข้างต้น ซึ่งจะไม่กล่าวถึงในที่นี้
อ่านบทช่วยสอน PyTorch เกี่ยวกับการสร้างสถาปัตยกรรมเครือข่ายของคุณเอง (หรือที่เรียกว่าโมดูล)
การถ่ายโอนการเรียนรู้ทำได้อย่างง่ายดายโดยการทำให้เป็นอนุกรม old_solver.nets (รายการโมดูลคบเพลิง) ลงในดิสก์ จากนั้นโหลดโมดูลเหล่านั้นและส่งผ่านไปยังตัวแก้ปัญหาใหม่:
old_solver.fit(max_epochs=...)# ... ดัมพ์ `old_solver.nets` ไปยังดิสก์# ... โหลดเครือข่ายจากดิสก์ เก็บไว้ใน `loaded_nets` ตัวแปรnew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
ขณะนี้เรากำลังพัฒนาฟังก์ชัน wrapper เพื่อบันทึก/โหลดเครือข่ายและตัวแปรภายในอื่นๆ ของ Solvers ในระหว่างนี้ คุณสามารถอ่านบทช่วยสอน PyTorch เกี่ยวกับการบันทึกและโหลดเครือข่ายของคุณได้
ใน neurodiffeq เครือข่ายได้รับการฝึกอบรมโดยการลดการสูญเสีย (ODE/PDE ตกค้าง) ให้เหลือน้อยที่สุด โดยประเมินบนชุดของจุดในโดเมน คะแนนจะถูกสุ่มตัวอย่างใหม่ทุกครั้ง เพื่อควบคุมจำนวน การกระจาย และขอบเขตขอบเขตของจุดสุ่มตัวอย่าง คุณสามารถระบุ generator การฝึกอบรม/การตรวจสอบความถูกต้องของคุณเองได้
จาก neurodiffeq.generators นำเข้า Generator1D# ค่าเริ่มต้น t_min=0.0, t_max=1.0, method='uniform', noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., noise_std=...)g2 = เครื่องกำเนิด1D(ขนาด=..., t_min=..., t_max=..., วิธีการ=..., noise_std=...)ตัวแก้ปัญหา = Solver1D(..., train_generator=g1, valid_generator=g2)
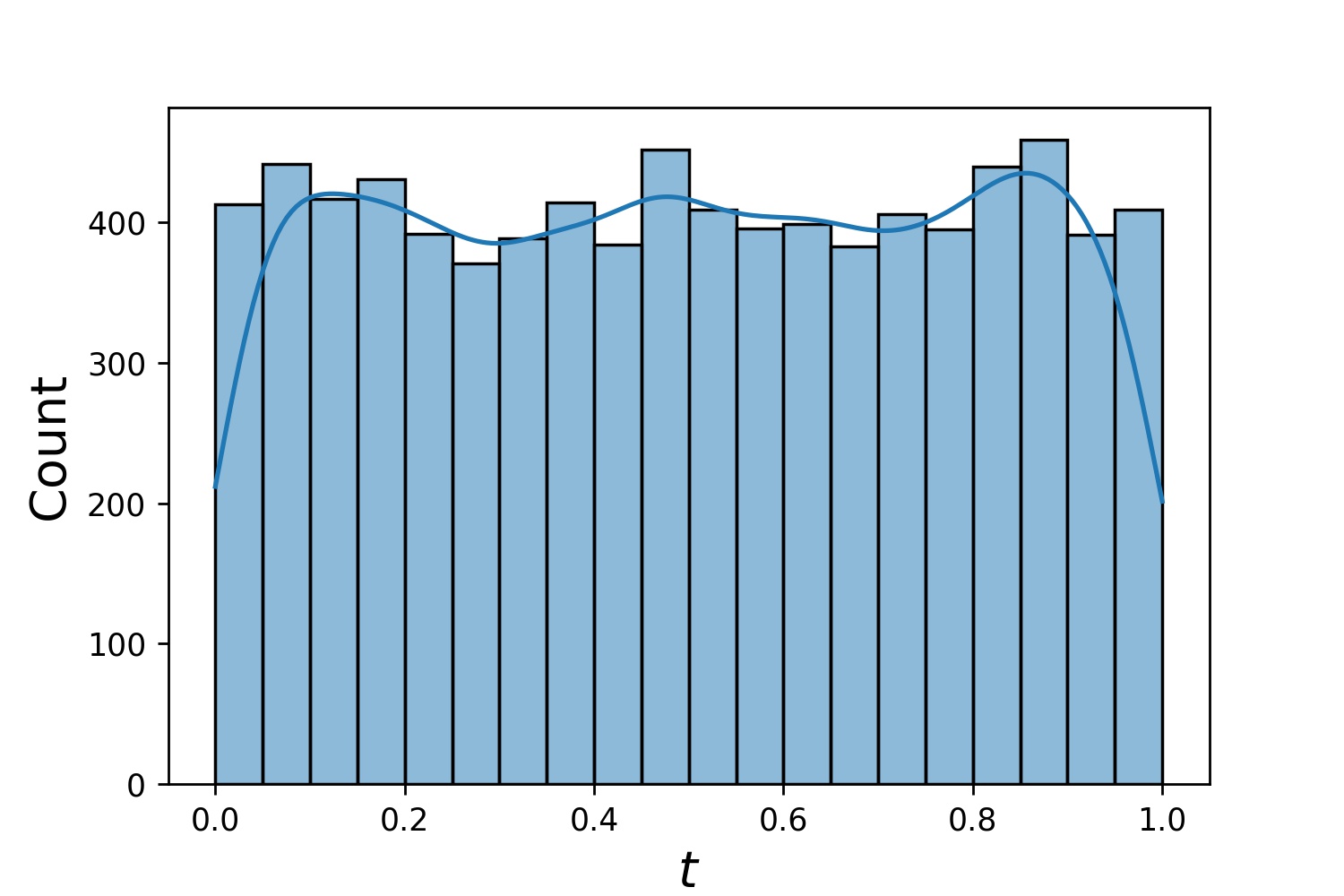
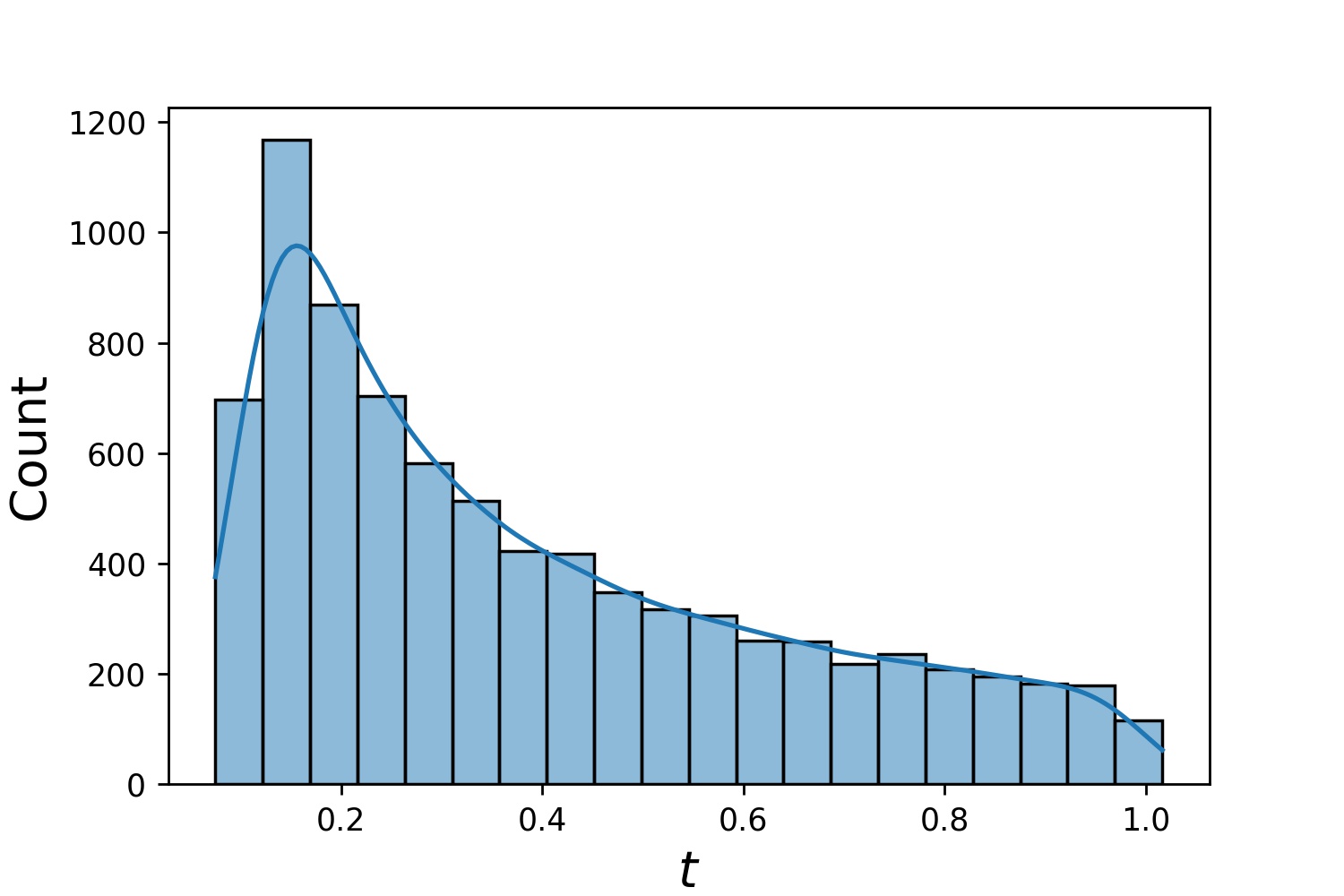
นี่คือตัวอย่างการแจกแจงของ Generator1D
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
 |  |
โปรดทราบว่าเมื่อมีการระบุทั้ง train_generator และ valid_generator t_min และ t_max สามารถละเว้นได้ใน Solver1D(...) ในความเป็นจริงแม้ว่าคุณจะผ่าน t_min , t_max , train_generator , valid_generator ด้วยกัน t_min และ t_max จะยังคงถูกละเว้น
คุณสมบัติที่ดีอีกประการหนึ่งของเครื่องกำเนิดไฟฟ้าก็คือคุณสามารถต่อเชื่อมเข้าด้วยกันได้
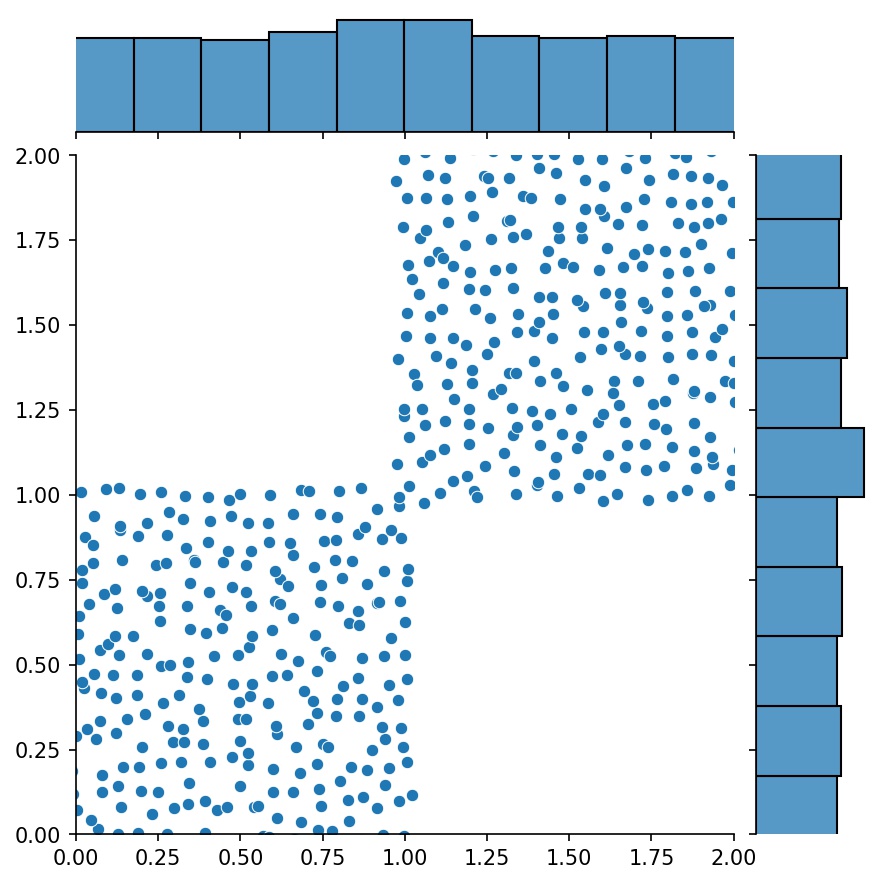
g1 = ตัวสร้าง2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = ตัวสร้าง2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))ก = g1 + g2
ในที่นี้ g จะเป็นเครื่องกำเนิดที่ส่งออกตัวอย่างที่รวมกันของ g1 และ g2
g1 | g2 | g1 + g2 |
|---|---|---|
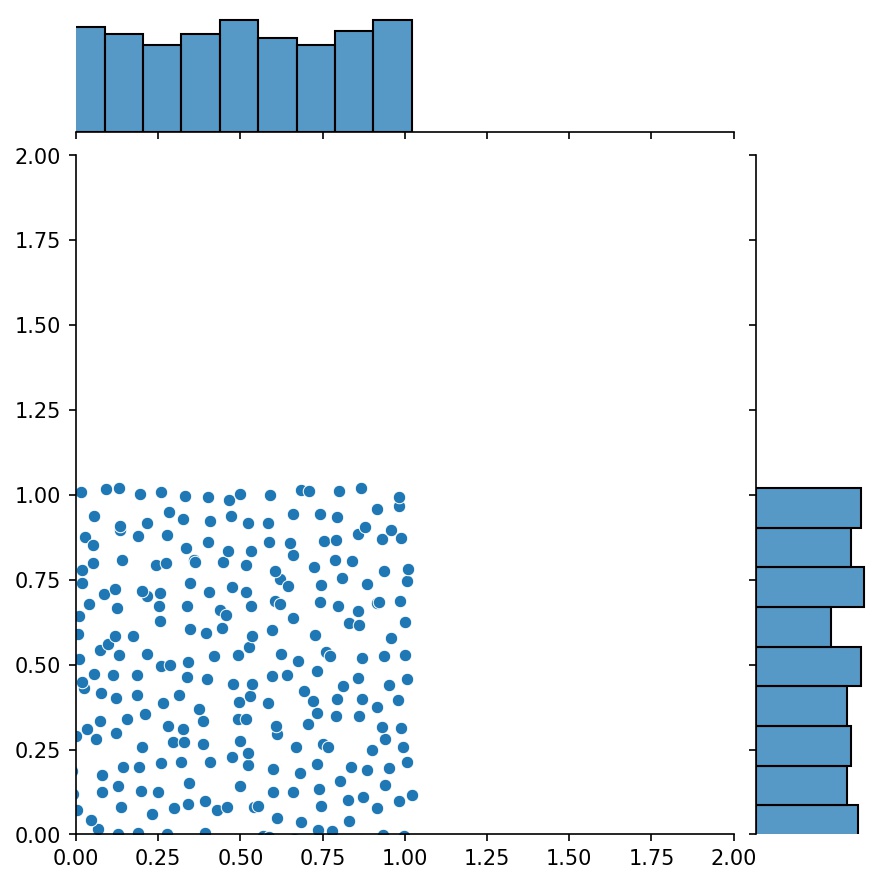 | 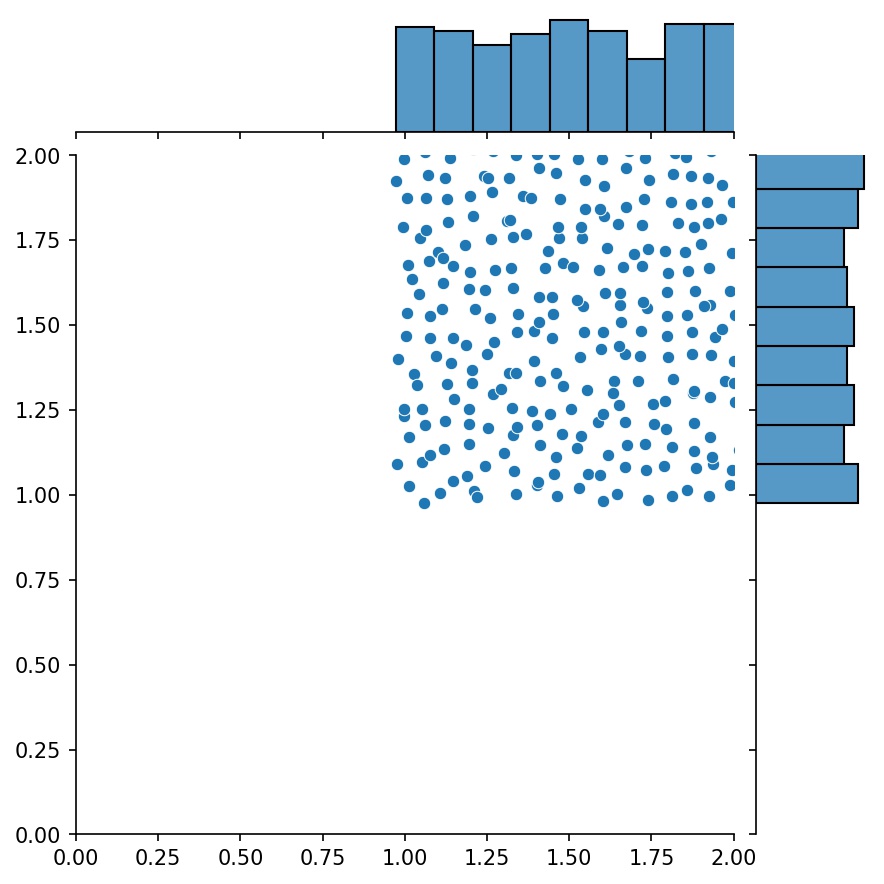 |  |
คุณสามารถใช้ Generator2D , Generator3D ฯลฯ สำหรับการสุ่มตัวอย่างจุดในมิติที่สูงกว่า แต่ยังมีวิธีอื่นอีกด้วย
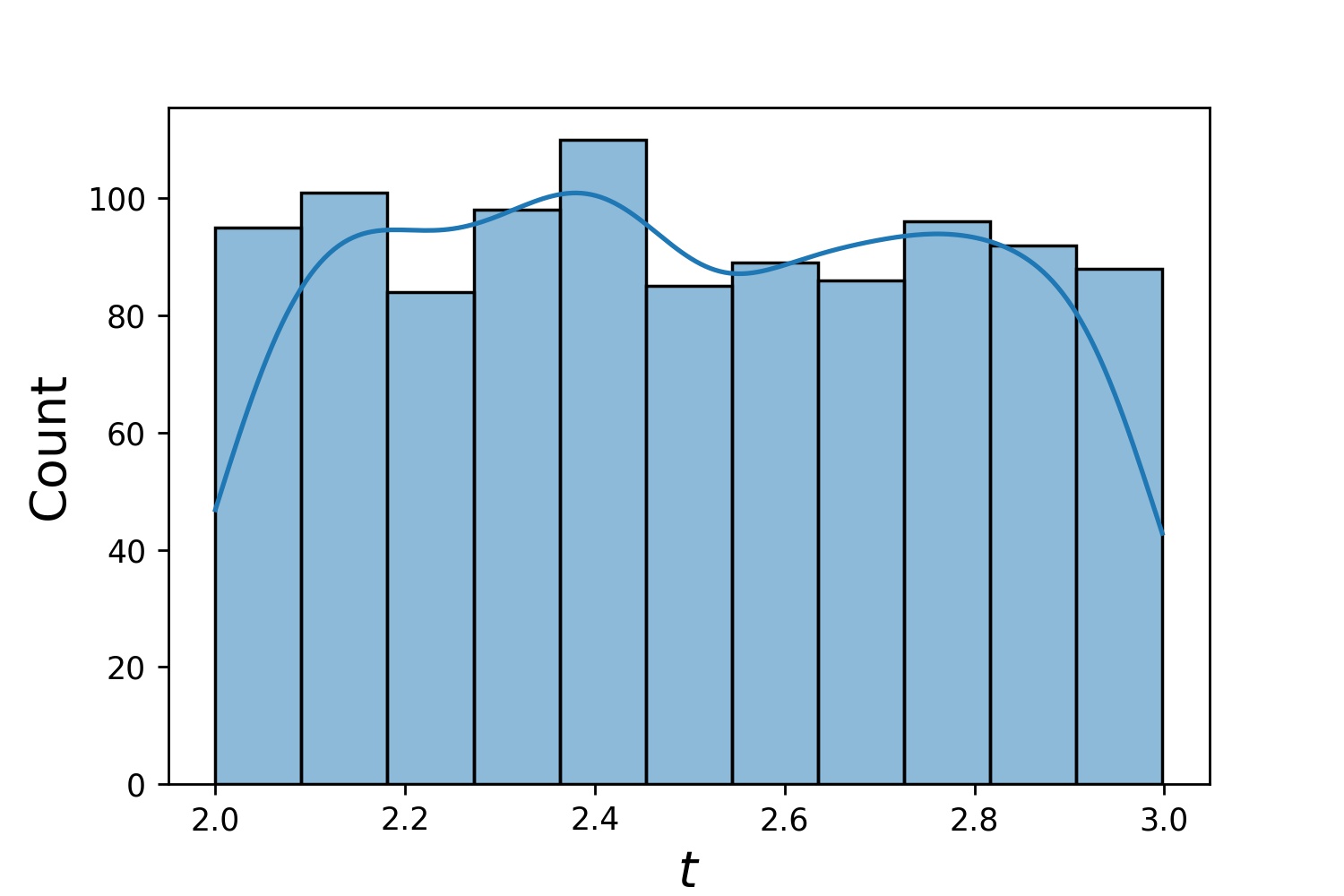
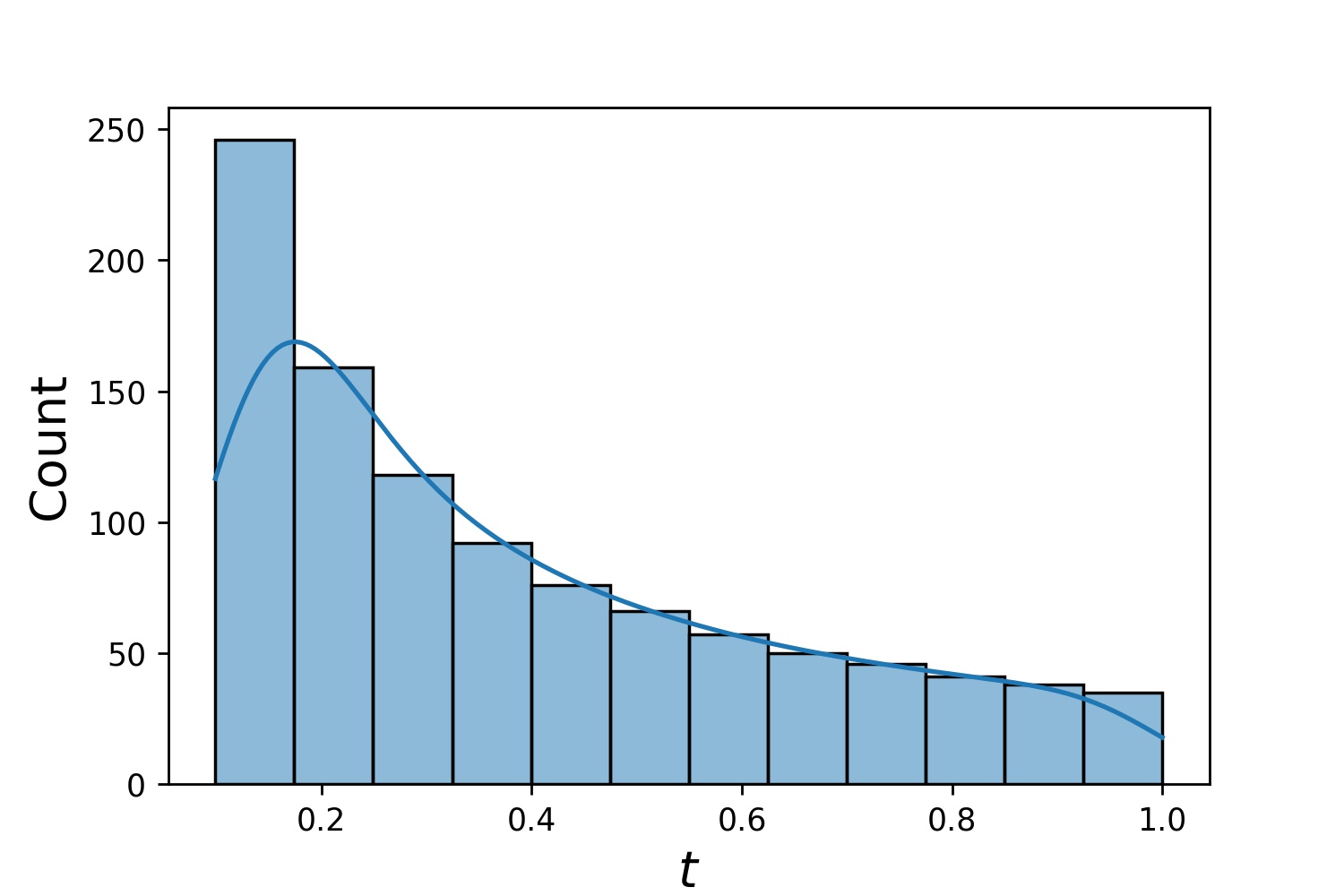
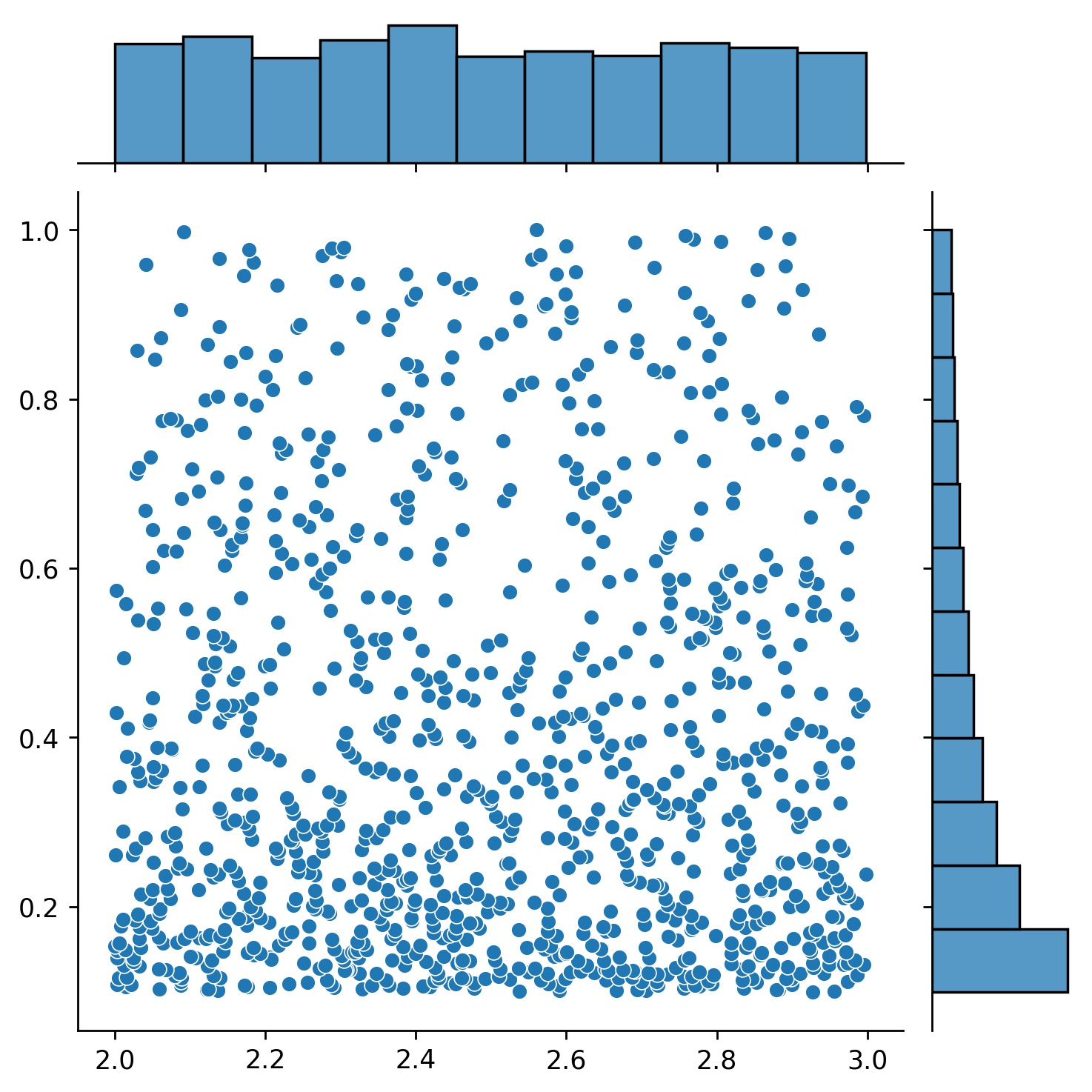
g1 = Generator1D(1024, 2.0, 3.0, method='uniform')g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy', noise_std=0.001)g = g1 * g2
ที่นี่ g จะเป็นเครื่องกำเนิดที่ให้ผล 1,024 จุดในรูปสี่เหลี่ยมผืนผ้า 2 มิติ (2,3) × (0.1,1) ทุกครั้ง พิกัด x ของพวกมันดึงมาจาก (2,3) โดยใช้ uniform กลยุทธ์ และพิกัด y ดึงมาจาก (0.1,1) โดยใช้กลยุทธ์ log-spaced-noisy
g1 | g2 | g1 * g2 |
|---|---|---|
 |  |  |
บางครั้ง การแก้สมการ หลายๆ ชุด พร้อมกันเป็นเรื่องที่น่าสนใจ ตัวอย่างเช่น คุณอาจต้องการแก้สมการเชิงอนุพันธ์ในรูปแบบ du/dt + λu = 0 ภายใต้เงื่อนไขเริ่มต้น u(0) = U0 คุณอาจต้องการแก้ปัญหานี้สำหรับ λ และ U0 ทั้งหมดพร้อมกัน โดยถือว่าพวกมันเป็นอินพุตของโครงข่ายประสาทเทียม
การใช้งานอย่างหนึ่งคือสำหรับปฏิกิริยาเคมี โดยไม่ทราบอัตราการเกิดปฏิกิริยา อัตราการเกิดปฏิกิริยาที่ต่างกันจะสอดคล้องกับสารละลายที่แตกต่างกัน และมีเพียงโซลูชันเดียวเท่านั้นที่ตรงกับจุดข้อมูลที่สังเกตได้ คุณอาจสนใจที่จะแก้ปัญหาเพื่อหากลุ่มสารละลายก่อน จากนั้นจึงกำหนดอัตราการเกิดปฏิกิริยาที่ดีที่สุด (หรือที่เรียกว่าพารามิเตอร์สมการ) ขั้นตอนที่สองเรียกว่า ปัญหาผกผัน
นี่คือตัวอย่างวิธีการใช้ neurodiffeq :
สมมติว่าเรามีสมการ du/dt + λu = 0 และเงื่อนไขเริ่มต้น u(0) = U0 โดยที่ λ และ U0 เป็นค่าคงที่ที่ไม่รู้จัก นอกจากนี้เรายังมีชุดข้อสังเกต t_obs และ u_obs ก่อนอื่นเราจะนำเข้า BundleSolver และ BundleIVP ซึ่งจำเป็นในการรับชุดโซลูชัน:
จาก neurodiffeq.conditions นำเข้า BundleIVP จาก neurodiffeq.solvers นำเข้า BundleSolver1Dimport matplotlib.pyplot เป็น pltimport numpy เป็น npimport torch จาก neurodiffeq import diff
เรากำหนดโดเมนของอินพุต t เช่นเดียวกับโดเมนของพารามิเตอร์ λ และ U0 . เรายังจำเป็นต้องตัดสินใจเกี่ยวกับลำดับของพารามิเตอร์ด้วย กล่าวคือ อันไหนควรเป็นพารามิเตอร์แรก และอันไหนควรเป็นพารามิเตอร์ตัวที่สอง สำหรับจุดประสงค์ของการสาธิตนี้ เราเลือก λ เป็นพารามิเตอร์ตัวแรก (ดัชนี 0) และ U0 เป็นพารามิเตอร์ตัวที่สอง (ดัชนี 1) การติดตามดัชนีของพารามิเตอร์เป็นสิ่งสำคัญมาก
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # พารามิเตอร์แรก, ดัชนี = 0U0_MIN, U0_MAX = 0.2, 0.6 # พารามิเตอร์วินาที, ดัชนี = 1
จากนั้นเราจะกำหนด conditions และ solver ตามปกติ ยกเว้นว่าเราใช้ BundleIVP และ BundleSolver1D แทน IVP และ Solver1D อินเทอร์เฟซของทั้งสองนี้คล้ายกับ IVP และ Solver1D มาก คุณสามารถดูข้อมูลเพิ่มเติมได้ในข้อมูลอ้างอิง API
# พารามิเตอร์สมการมาหลังจากอินพุต (โดยปกติจะเป็นพิกัดชั่วคราวและเชิงพื้นที่)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# อาร์กิวเมนต์ของคำหลักจะต้องตั้งชื่อว่า "u_0" ใน BundleIVP หากคุณใช้อย่างอื่น เช่น `y0`, `u0` ฯลฯ มันจะใช้งานไม่ได้ Conditions = [BundleIVP(t_0=0, u_0=None, Bundle_param_lookup={'u_0': 1}) # u_0 has ดัชนี 1]ตัวแก้ปัญหา = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # u_0 มีดัชนี 0; u_0 มีดัชนี 1theta_max=[LAMBDA_MAX, U0_MAX], # u_0 มีดัชนี 0; พารามิเตอร์สมการซึ่งมีดัชนี 0n_batches_valid=1
- เนื่องจาก λ เป็นพารามิเตอร์ในสมการ และ λ U0 พารามิเตอร์ในเงื่อนไขเริ่มต้น เราจึงต้องรวม แล ไว้ใน diff_eq และ U0 ไว้ในเงื่อนไข หากมีพารามิเตอร์อยู่ในทั้งสมการและเงื่อนไข จะต้องรวมไว้ในทั้งสองตำแหน่ง องค์ประกอบทั้งหมดของ conditions ที่ส่งไปยัง BundleSovler1D ต้องเป็นเงื่อนไข Bundle* แม้ว่าจะไม่มีพารามิเตอร์ก็ตาม
ตอนนี้เราสามารถฝึกมันและรับวิธีแก้ปัญหาได้ตามปกติ
solver.fit(max_epochs=1,000)solution = solver.get_solution(ดีที่สุด=True)
วิธีแก้ปัญหาคาดว่าจะมีอินพุตสามตัว - t , λ และ U0 อินพุตทั้งหมดจะต้องมีรูปร่างเหมือนกัน ตัวอย่างเช่น หากคุณสนใจที่จะแก้ไข แลม λ=4 และ U0=0.4 และวางแผนวิธีแก้ปัญหา u กับ t ∈ [0,1] คุณสามารถทำสิ่งต่อไปนี้ได้
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0.4 * np.ones_like(t)u = โซลูชัน (t, lmd, u0, to_numpy=True) นำเข้า matplotlib.pyplot เป็น pltplt .plot(t, คุณ)
เมื่อคุณมี solution แบบรวม คุณจะพบชุดพารามิเตอร์ (λ, U0) ที่ตรงกับจุดข้อมูลที่สังเกตได้ (t_i, u_i) ได้ใกล้เคียงที่สุด สามารถทำได้โดยใช้การไล่ระดับสีแบบง่าย ในตัวอย่างของเล่นต่อไปนี้ เราถือว่ามีจุดข้อมูลเพียงสามจุด u(0.2) = 0.273 , u(0.5)=0.129 และ u(0.8) = 0.0609 ต่อไปนี้เป็นเวิร์กโฟลว์ PyTorch แบบคลาสสิก
# ข้อมูลที่สังเกตได้ pointt_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# การเริ่มต้นแบบสุ่ม ของ แล และ U0; ติดตามการไล่ระดับสีlmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = torch.optim.Adam([lmd_tensor.requires_grad_(True) u0_tensor.requires_grad_(จริง)], lr=1e-2)# รันการไล่ระดับสีเป็นเวลา 10,000 ยุคสำหรับ _ ในช่วง (10,000): เอาต์พุต = โซลูชัน (t_obs, lmd_tensor * torch.ones_like (t_obs), u0_tensor * torch.ones_like (t_obs)) การสูญเสีย = ((เอาต์พุต - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
พิมพ์ (f"แล = {lmd_tensor.item()}, U0={u0_tensor.item()}, การสูญเสีย = {loss.item()}") เรียบง่าย. เมื่อนำเข้า neurodiffeq ไลบรารีจะตรวจจับโดยอัตโนมัติว่า CUDA มีอยู่ในเครื่องของคุณหรือไม่ เนื่องจากไลบรารี่ใช้ PyTorch จึงจะตั้งค่าประเภทเทนเซอร์เริ่มต้นเป็น torch.cuda.DoubleTensor หากพบอุปกรณ์ GPU ที่รองรับ
โปรดดูส่วนเครือข่ายที่กำหนดเองและการถ่ายโอนการเรียนรู้
วิธี PyTorch มาตรฐาน
สร้างเครือข่ายของคุณตามที่อธิบายไว้ในเครือข่ายที่กำหนดเอง: nets = [FCNN(), FCN(), ...]
สร้างอินสแตนซ์ของเครื่องมือเพิ่มประสิทธิภาพแบบกำหนดเองและส่งพารามิเตอร์ทั้งหมดของเครือข่ายเหล่านี้ไปให้
พารามิเตอร์ = [p สำหรับ net ใน nets สำหรับ p ใน net.parameters()] # รายการพารามิเตอร์ของเครือข่ายทั้งหมดMY_LEARNING_RATE = 5e-3optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
ส่งทั้ง nets และ optimizer ของคุณไปยังตัวแก้ปัญหา: solver = Solver1D(..., nets=nets, optimizer=optimizer)
ต่างจากวิธีการตัวเลขแบบดั้งเดิม (FEM, FVM ฯลฯ) โซลูชันที่ใช้ NN จำเป็นต้องมีการปรับแต่งขั้นสูงบางอย่าง ไลบรารีนำเสนอความยืดหยุ่นสูงสุดในการลองใช้ไฮเปอร์พารามิเตอร์ผสมกัน
หากต้องการใช้สถาปัตยกรรมเครือข่ายอื่น คุณสามารถส่งผ่าน torch.nn.Module ที่คุณกำหนดเองได้
หากต้องการใช้เครื่องมือเพิ่มประสิทธิภาพอื่น คุณสามารถส่งผ่านเครื่องมือเพิ่มประสิทธิภาพของคุณเองไปยัง solver = Solver(..., optimizer=my_optim)
หากต้องการใช้การกระจายตัวอย่างที่แตกต่างกัน คุณสามารถใช้ตัวสร้างในตัวหรือเขียนตัวสร้างของคุณเองตั้งแต่เริ่มต้นได้
หากต้องการใช้ขนาดการสุ่มตัวอย่างที่แตกต่างกัน คุณสามารถปรับแต่งตัวสร้างหรือเปลี่ยน solver = Solver(..., n_batches_train)
หากต้องการเปลี่ยนไฮเปอร์พารามิเตอร์แบบไดนามิกระหว่างการฝึก ให้ดูคุณสมบัติการโทรกลับของเรา
อย่าใช้ ReLU ในการเปิดใช้งาน เนื่องจากอนุพันธ์อันดับสองของมันคือ 0 เหมือนกัน
ปรับขนาด PDE/ODE ของคุณใหม่ในรูปแบบไร้มิติ โดยควรให้ทุกอย่างอยู่ในช่วง [0,1] การทำงานกับโดเมนเช่น [0,1000000] มีแนวโน้มที่จะล้มเหลวเนื่องจาก a) PyTorch เริ่มต้นน้ำหนักของโมดูลให้มีขนาดค่อนข้างเล็ก และ b) ฟังก์ชันการเปิดใช้งานส่วนใหญ่ (เช่น Sigmoid, Tanh, Swish) ส่วนใหญ่จะไม่เป็นเชิงเส้นใกล้กับ 0
หาก PDE/ODE ของคุณซับซ้อนเกินไป ลองพิจารณาการเรียนรู้ตามหลักสูตร เริ่มต้นการฝึกอบรมเครือข่ายของคุณบนโดเมนขนาดเล็ก จากนั้นค่อยๆ ขยายจนครอบคลุมทั้งโดเมน
ทุกคนยินดีที่จะมีส่วนร่วมในโครงการนี้
เมื่อสนับสนุนพื้นที่เก็บข้อมูลนี้ เราจะพิจารณากระบวนการต่อไปนี้:
เปิดประเด็นเพื่อหารือเกี่ยวกับการเปลี่ยนแปลงที่คุณวางแผนจะทำ
ผ่านแนวทางการบริจาค
ทำการเปลี่ยนแปลงบนที่เก็บแบบแยกส่วนและอัปเดต README.md หากมีการเปลี่ยนแปลงกับอินเทอร์เฟซ
เปิดคำขอดึง