การใช้อัลกอริทึม AI Minimax ในเกม Tic-Tac-Toe (หรือ Noughts and Crosses) ลองมัน: Tic-tac-toe - Minimax
เพื่อแก้ปัญหาเกมโดยใช้ AI เราจะแนะนำแนวคิดของแผนผังเกมตามด้วยอัลกอริธึมขั้นต่ำ สถานะต่างๆ ของเกมจะแสดงโดยโหนดในแผนผังเกม ซึ่งคล้ายกับปัญหาการวางแผนข้างต้นมาก ความคิดแตกต่างเพียงเล็กน้อย ในแผนผังเกม โหนดจะถูกจัดเรียงในระดับที่สอดคล้องกับเทิร์นของผู้เล่นแต่ละคนในเกม ดังนั้นโหนด "ราก" ของแผนผัง (โดยปกติจะแสดงที่ด้านบนของแผนภาพ) เป็นตำแหน่งเริ่มต้นในเกม ในโอเอกซ์ นี่จะเป็นตารางว่างที่ยังไม่มีการเล่น Xs หรือ Os ภายใต้รูท ในระดับที่สอง มีสถานะที่เป็นไปได้ที่อาจเป็นผลมาจากการเคลื่อนไหวของผู้เล่นคนแรก ไม่ว่าจะเป็น X หรือ O เราเรียกโหนดเหล่านี้ว่า "ลูก" ของโหนดรูท
แต่ละโหนดในระดับที่สอง จะมีเพิ่มเติมเมื่อลูก ๆ ของมันโหนดสถานะที่สามารถเข้าถึงได้จากการเคลื่อนไหวของผู้เล่นฝ่ายตรงข้าม สิ่งนี้จะดำเนินต่อไปทีละระดับจนกระทั่งถึงจุดที่เกมจบลง ในโอเอกซ์ หมายความว่าผู้เล่นคนใดคนหนึ่งได้แถวสามและชนะ หรือกระดานเต็มและเกมจบลงด้วยการเสมอกัน
Minimax เป็นปัญญาประดิษฐ์ที่ใช้ในเกมสำหรับผู้เล่นสองคน เช่น โอเอกซ์ หมากฮอส หมากรุกและโก เกมนี้เรียกว่าเกมผลรวมเป็นศูนย์ เพราะในทางคณิตศาสตร์ ผู้เล่นคนหนึ่งชนะ (+1) และผู้เล่นอีกคนแพ้ (-1) หรือทั้งสองคนไม่ชนะ (0)
การค้นหาอัลกอริธึมแบบวนซ้ำการเคลื่อนไหวที่ดีที่สุดที่ทำให้ผู้เล่น Max ชนะหรือไม่แพ้ (เสมอ) โดยจะพิจารณาสถานะปัจจุบันของเกมและการเคลื่อนไหวที่มีอยู่ในสถานะนั้น จากนั้นจะเล่นในแต่ละการเคลื่อนไหวที่ถูกต้อง (สลับต่ำ สุด และ สูงสุด ) จนกว่าจะพบสถานะเทอร์มินัล (ชนะ เสมอ หรือแพ้)
อัลกอริธึมได้รับการศึกษาโดยหนังสือ Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009) รหัสเทียม (ดัดแปลง):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
ตอนนี้เราจะเห็นแต่ละส่วนของรหัสเทียมนี้พร้อมกับการนำ Python ไปใช้ การใช้งาน Python มีอยู่ในพื้นที่เก็บข้อมูลนี้ ก่อนอื่น ให้พิจารณาว่า:
คณะกรรมการ = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
สูงสุด = +1
นาที = -1
MAX อาจเป็น X หรือ O และ MIN อาจเป็น O หรือ X อะไรก็ได้ กระดานมีขนาด 3x3
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]ผู้เล่นทั้งสองเริ่มต้นด้วยคะแนนที่แย่ที่สุดของคุณ หากผู้เล่นมีค่าสูงสุด คะแนนจะเป็น -อนันต์ มิฉะนั้นหากผู้เล่นเป็น MIN คะแนนจะเป็น + อนันต์ หมายเหตุ: infinity เป็นนามแฝงสำหรับ inf (จากโมดูลคณิตศาสตร์ใน Python)
การเคลื่อนไหวที่ดีที่สุดบนกระดานคือ [-1, -1] (แถวและคอลัมน์) สำหรับทุกคน
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreหากความลึกเท่ากับศูนย์ แสดงว่ากระดานไม่มีเซลล์ว่างใหม่ให้เล่น หรือหากผู้เล่นชนะ เกมจะจบลงที่ MAX หรือ MIN ดังนั้นคะแนนสำหรับสถานะนั้นจะถูกส่งกลับ
ตอนนี้เราจะเห็นส่วนหลักของโค้ดนี้ที่มีการเรียกซ้ำ
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yสำหรับการเคลื่อนไหวที่ถูกต้องแต่ละครั้ง (เซลล์ว่าง):
การย้าย (+1 หรือ -1) บนกระดานถูกยกเลิก และแถว คอลัมน์จะถูกรวบรวม
ขั้นตอนต่อไปคือการเปรียบเทียบคะแนนกับคะแนนที่ดีที่สุด
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreสำหรับผู้เล่น MAX จะได้รับคะแนนที่มากขึ้น สำหรับผู้เล่น MIN จะได้รับคะแนนที่ต่ำกว่า และสุดท้ายการเคลื่อนไหวที่ดีที่สุดก็กลับคืนมา อัลกอริธึมสุดท้าย:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best ด้านล่าง การเคลื่อนไหวที่ดีที่สุดจะอยู่ตรงกลางเนื่องจากค่าสูงสุดอยู่ที่โหนดที่ 2 ทางด้านซ้าย
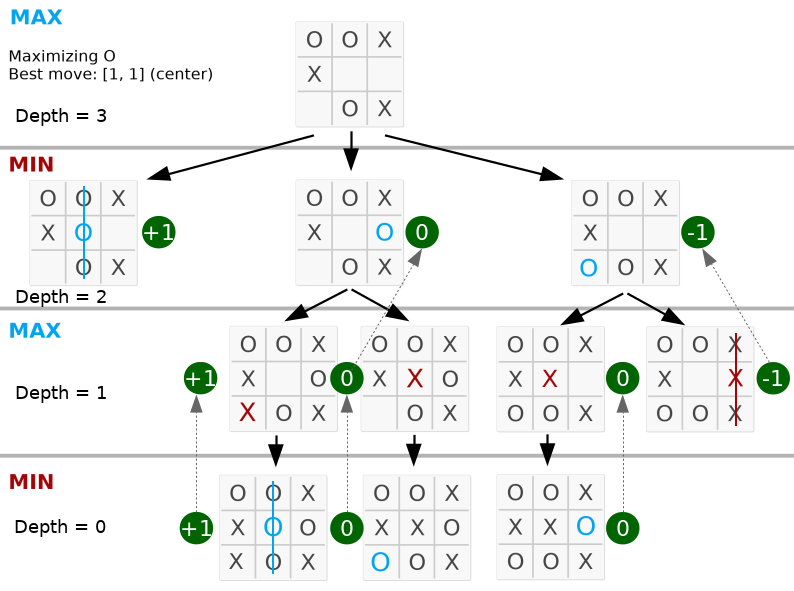
ลองดูว่าความลึกเท่ากับการเคลื่อนไหวที่ถูกต้องบนกระดาน รหัสที่สมบูรณ์มีอยู่ใน py_version/
แผนผังเกมแบบง่าย:
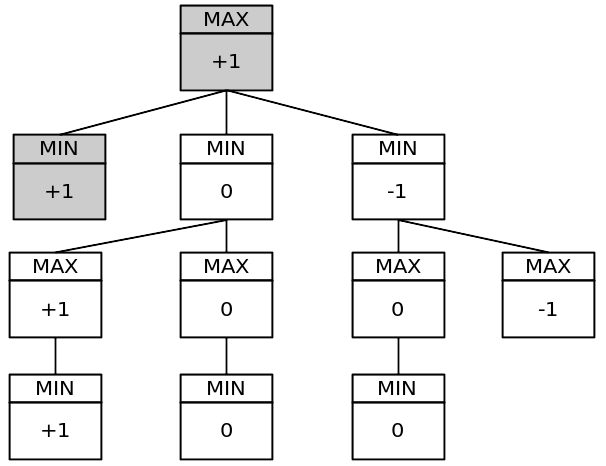
ต้นไม้นั้นมี 11 โหนด แผนผังเกมเต็มมี 549.946 โหนด! คุณสามารถทดสอบได้โดยใส่ตัวแปรโกลบอลแบบคงที่ในโปรแกรมของคุณและเพิ่มค่าสำหรับการเรียกใช้ฟังก์ชัน minimax แต่ละครั้งต่อเทิร์น
ในเกมที่ซับซ้อนมากขึ้น เช่น หมากรุก การค้นหาแผนผังเกมทั้งหมดเป็นเรื่องยาก อย่างไรก็ตาม การตัดแต่งกิ่งอัลฟ่า–เบต้าเป็นวิธีการปรับให้เหมาะสมสำหรับอัลกอริธึมขั้นต่ำสุดซึ่งช่วยให้เรามองข้ามบางสาขาในแผนผังการค้นหาได้ เนื่องจากเขาจะตัดโหนดที่ไม่เกี่ยวข้อง (แผนผังย่อย) ในการค้นหา สำหรับข้อมูลเพิ่มเติม โปรดดู: