การทดสอบความเท่าเทียมกันสามารถนำไปใช้เพื่อประเมินว่าผลกระทบที่สังเกตได้จากตัวทำนายแต่ละตัวในแบบจำลองการถดถอยหลายตัวนั้นมีขนาดเล็กพอที่จะพิจารณาทางสถิติและในทางปฏิบัติ (Alter & Counsell, 2021) สำหรับข้อมูลเพิ่มเติมโปรดดูหน้า OSF และ/หรือ preprint ที่ใช้งานได้อย่างอิสระบน psyarxiv
ฟังก์ชั่นต่อไปนี้เสนอทางเลือกตามความเท่าเทียมกันที่เหมาะสมสำหรับการสรุปผลกระทบเล็กน้อยระหว่างตัวทำนายและผลลัพธ์ในการถดถอยหลายครั้ง
ฟังก์ชั่น R เหล่านี้ได้รับการออกแบบมาเพื่อรองรับบริบทการวิจัยที่หลากหลายได้อย่างง่ายดายโดยมีหรือไม่มีการเข้าถึงชุดข้อมูลเต็มรูปแบบ ฟังก์ชั่นทั้งสองคือ reg.equiv.fd() และ reg.equiv() ให้ผลลัพธ์ที่คล้ายกัน แต่แตกต่างกันไปตามประเภทของข้อมูลอินพุตที่ผู้ใช้ต้องการ
โดยเฉพาะฟังก์ชั่นแรก reg.equiv.fd() ต้องการชุดข้อมูลและโมเดลเต็มรูปแบบในวัตถุ R ( lm ) ในขณะที่ที่สองไม่ได้ reg.equiv() มีไว้สำหรับนักวิจัยที่ไม่สามารถเข้าถึงชุดข้อมูลที่สมบูรณ์ แต่ยังต้องการประเมินการขาดการเชื่อมโยงของตัวทำนายบางอย่างกับตัวแปรผลลัพธ์ในการถดถอยหลายครั้งเช่นโดยใช้ข้อมูลที่แสดงในส่วนผลลัพธ์หรือ ตารางที่รายงานในบทความที่เผยแพร่
reg.equiv.fd() : ชุดข้อมูลเต็มรูปแบบที่ต้องการdatfra= a data frame (เช่น mtcars)model= the model, วัตถุ LM (เช่น mod1 , โดยที่ mod1<- mpg~hp+cyl )delta= ขนาดเอฟเฟกต์ที่เล็กที่สุดที่น่าสนใจ (SESOI) ขนาดเอฟเฟกต์ที่มีความหมายน้อยที่สุด (MMEs) หรือขอบเขตบนของช่วงเวลาที่เทียบเท่า (?) (เช่น .15)predictor= ชื่อของตัวทำนายที่จะทดสอบ (เช่น "cyl" )test= ประเภทการทดสอบถูกตั้งค่าโดยอัตโนมัติเป็นสองการทดสอบด้านเดียว (TOST; Schuirmann, 1987) ตัวเลือกอื่นคือ Anderson-Hauck (Ah; Anderson & Hauck, 1983)std= เดลต้า (หรือ, sesoi) เป็นชุดเป็นมาตรฐานตามค่าเริ่มต้น ระบุ std=FALSE เพื่อรับหน่วยที่ไม่ได้มาตรฐานalpha= อัตราความผิดพลาดประเภทที่ 1 เล็กน้อยถูกตั้งค่าเป็น. 05 โดยค่าเริ่มต้น หากต้องการเปลี่ยนแปลงเพียงระบุระดับอัลฟ่า เช่น alpha=.10 reg.equiv.fd() ตัวอย่าง: 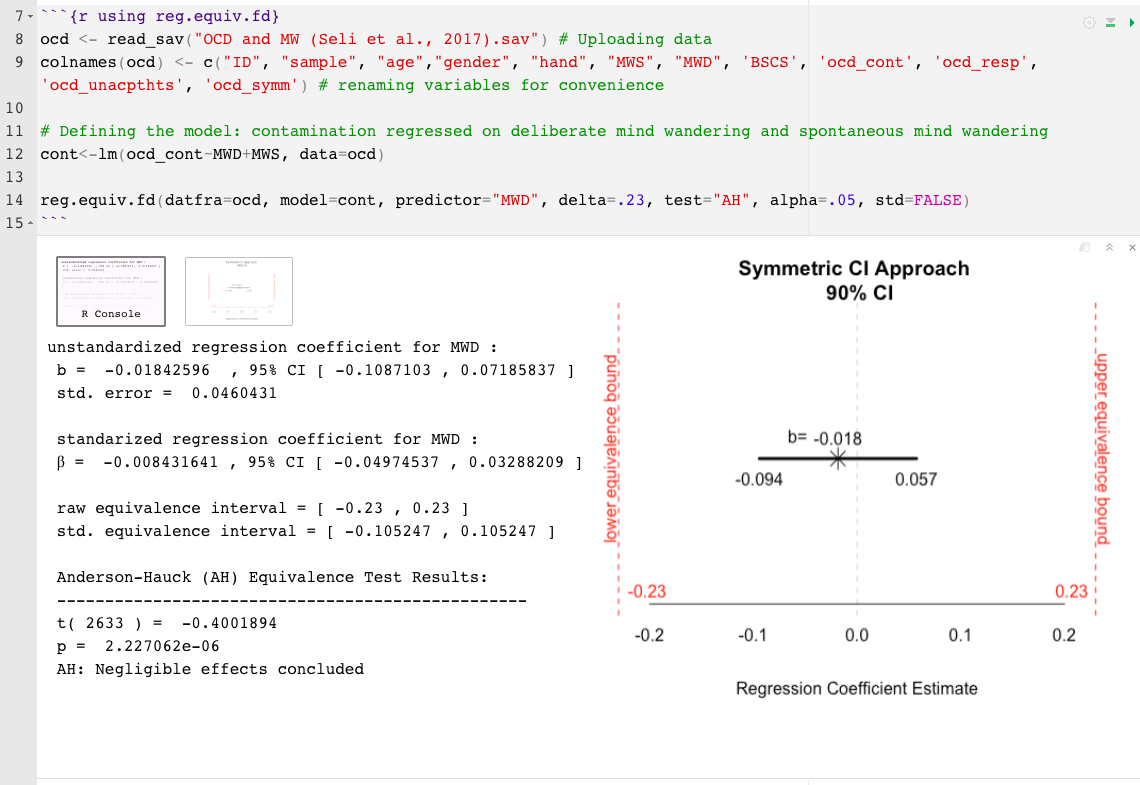
reg.equiv() : ไม่ จำเป็นต้องใช้ชุดข้อมูลเต็มรูปแบบb= ขนาดเอฟเฟกต์โดยประมาณที่เกี่ยวข้องกับตัวทำนายที่น่าสนใจซึ่งอาจเป็นมาตรฐานหรือไม่ได้มาตรฐาน (เช่น .02)se= ข้อผิดพลาดมาตรฐานที่เกี่ยวข้องกับขนาดเอฟเฟกต์ของตัวทำนายที่น่าสนใจ (หากขนาดเอฟเฟกต์เป็นมาตรฐานตรวจสอบให้แน่ใจว่าค่า se เชื่อมโยงกับมาตรฐานและไม่ใช่เอฟเฟกต์ดิบ)p= จำนวนตัวทำนายทั้งหมดในแบบจำลองการถดถอย (ไม่รวมการสกัดกั้น)n= ขนาดตัวอย่างdelta= ขนาดเอฟเฟกต์ที่เล็กที่สุดที่น่าสนใจ (SESOI) ขนาดเอฟเฟกต์ที่มีความหมายน้อยที่สุด (MMEs) หรือขอบเขตบนของช่วงเวลาที่เทียบเท่า (?) (เช่น .15)predictor= ชื่อของตัวทำนายที่จะทดสอบ (เช่น "cyl" )test= ประเภทการทดสอบถูกตั้งค่าโดยอัตโนมัติเป็นสองการทดสอบด้านเดียว (TOST; Schuirmann, 1987) ตัวเลือกอื่นคือ Anderson-Hauck (Ah; Anderson & Hauck, 1983)std= เดลต้า (หรือ sesoi) และขนาดเอฟเฟกต์ที่ระบุถูกตั้งค่าเป็นมาตรฐานตามค่าเริ่มต้น ระบุ std=FALSE เพื่อรับหน่วยที่ไม่ได้มาตรฐานalpha= อัตราความผิดพลาดประเภทที่ 1 เล็กน้อยถูกตั้งค่าเป็น. 05 โดยค่าเริ่มต้น หากต้องการเปลี่ยนแปลงเพียงระบุระดับอัลฟ่า เช่น alpha=.10 reg.equiv() ตัวอย่าง: 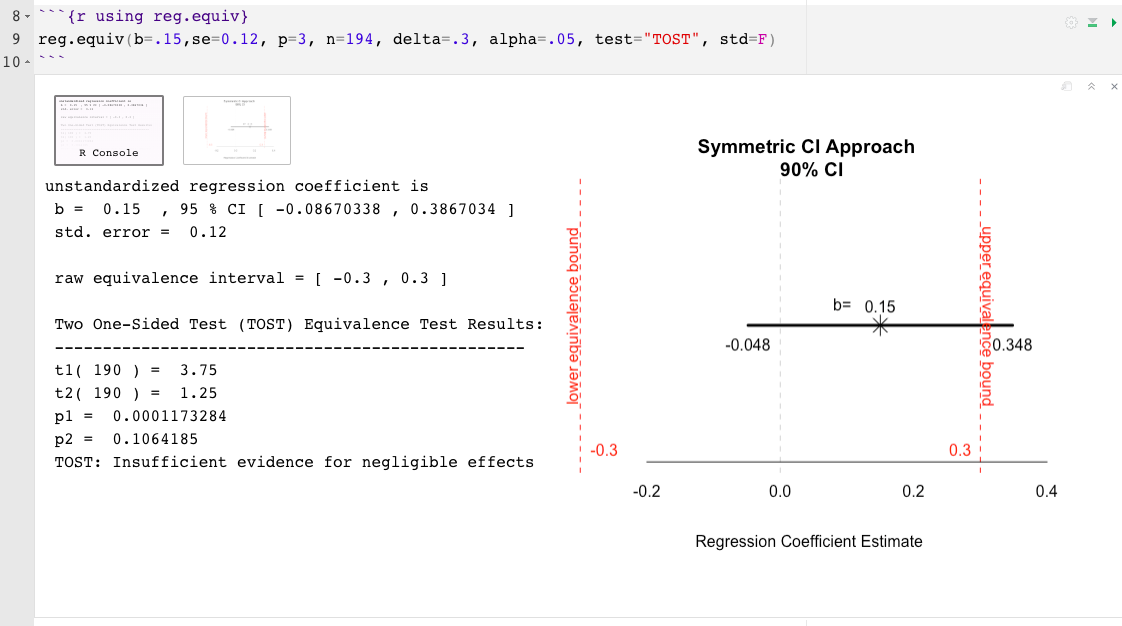
การทดสอบความเท่าเทียมเป็นวิธีการที่ออกแบบมาภายในกรอบการทดสอบความสำคัญ Null-Hypothesis (NHST) NHST ได้รับการวิพากษ์วิจารณ์อย่างหนักจากการพึ่งพามากเกินไปเกี่ยวกับผลลัพธ์แบบแบ่งขั้วของค่า P โดยไม่พิจารณาขนาดของเอฟเฟกต์หรือผลกระทบในทางปฏิบัติ (เช่นคัมมิง, 2012; Fidler & Loftus, 2009; Harlow, 1997; Kirk, 2003, 2003, 2003, 2003; Lee, 2016 2014) นักวิจัยจะต้องคำนึงถึงข้อ จำกัด ของ NHST และคลี่คลายด้านการปฏิบัติและสถิติของผลการทดสอบ
เพื่อลดข้อ จำกัด ของค่า P จะมีข้อมูลมากขึ้นใน การตีความขนาดและความแม่นยำของเอฟเฟกต์ที่สังเกตได้ นอกเหนือจากบทสรุปของ“ ผลกระทบเล็กน้อย” หรือ“ หลักฐานไม่เพียงพอสำหรับผลกระทบเล็กน้อย” ผลกระทบที่สังเกตได้ควรตีความในความสัมพันธ์กับขอบเขตความเท่าเทียมกันขอบเขตของความไม่แน่นอนและผลกระทบเชิงปฏิบัติของพวกเขา (หรือขาดมัน) ด้วยเหตุผลนี้ ฟังก์ชั่น R ทั้งสองที่นำเสนอที่นี่จึงรวมถึงการแสดงกราฟิกของเอฟเฟกต์ที่สังเกตได้และความไม่แน่นอนที่เกี่ยวข้องกับช่วงเวลาที่เทียบเท่า พล็อตที่เกิดขึ้นช่วยในการแสดงให้เห็นว่าเอฟเฟกต์ที่สังเกตได้ใกล้หรือกว้างและกว้างหรือแคบลงและระยะขอบของข้อผิดพลาดนั้นมาจากขอบเขตที่เท่าเทียมกัน การอนุมานเกี่ยวกับสัดส่วนและตำแหน่งของแถบความเชื่อมั่นที่เกี่ยวข้องกับช่วงเวลาที่เทียบเท่าสามารถช่วยตีความผลลัพธ์ที่มากกว่าและสูงกว่าค่า P