โครงการนี้ได้ย้ายไปที่ Boost (คณิตศาสตร์/ความแตกต่าง/autodiff) และที่เก็บนี้จะไม่ได้รับการปรับปรุงอีกต่อไป
| สาขา | เทรวิส | ผู้ที่มีความสามารถ | codecov.io |
|---|---|---|---|
master | |||
develop |
Autodiff เป็นไลบรารี C ++ เฉพาะส่วนหัวที่อำนวยความสะดวกในการสร้างความแตกต่างอัตโนมัติ (โหมดไปข้างหน้า) ของฟังก์ชั่นทางคณิตศาสตร์ของตัวแปรเดี่ยวและหลายตัวแปร
การใช้งานนี้ขึ้นอยู่กับการขยายซีรีย์เทย์เลอร์ของฟังก์ชั่นการวิเคราะห์ F ณ จุด X₀ :
แนวคิดที่สำคัญของ Autodiff คือการทดแทนตัวเลขที่มีพหุนามในการประเมิน F (x₀) โดยการแทนที่หมายเลข x₀ ด้วยพหุนามลำดับแรก X₀+ε และใช้อัลกอริทึมเดียวกันเพื่อคำนวณ F (x₀+ε) , พหุนามที่เกิดขึ้นใน ε ประกอบด้วยอนุพันธ์ของฟังก์ชัน f '(x₀) , f' '(x₀) , f '' '(x₀) , ... ภายในค่าสัมประสิทธิ์ แต่ละสัมประสิทธิ์มีค่าเท่ากับอนุพันธ์ของคำสั่งที่เกี่ยวข้องหารด้วยแฟคทอเรียลของคำสั่ง
โดยละเอียดมากขึ้นสมมติว่ามีความสนใจในการคำนวณอนุพันธ์ N แรกของ F ที่ x₀ หากไม่มีการสูญเสียความแม่นยำในการคำนวณอนุพันธ์คำศัพท์ทั้งหมด O (ε n+1 ) ซึ่งรวมถึงพลังของ ε มากกว่า n สามารถยกเลิกได้ (นี่เป็นเพราะความจริงที่ว่าแต่ละคำในพหุนามขึ้นอยู่กับคำศัพท์ที่เท่าเทียมกันและต่ำกว่าภายใต้การดำเนินการทางคณิตศาสตร์) ภายใต้กฎการตัดทอนเหล่านี้ F ให้การเปลี่ยนแปลงพหุนามกับพหุนาม:
ความสามารถของ C ++ ในการโอเวอร์โหลดตัวดำเนินการและฟังก์ชั่นช่วยให้สามารถสร้างคลาส fvar ที่แสดงถึงพหุนามใน ε ดังนั้นอัลกอริทึมเดียวกัน F ที่คำนวณค่าตัวเลขของ y₀ = f (x₀) เมื่อเขียนเพื่อยอมรับและส่งคืนตัวแปรของประเภททั่วไป (เทมเพลต) ยังใช้ในการคำนวณพหุนาม ʃ n y n εⁿ = f (x₀+ ε) อนุพันธ์ f (n) (x₀) จะพบได้จากผลิตภัณฑ์ของแฟคทอเรียลที่เกี่ยวข้อง n! และสัมประสิทธิ์ y n :

#include <boost/math/difference/autodiff.hpp> #include <iostream> แม่แบบ <typename t>
t Fourth_Power (t const & x) {
t x4 = x * x; // retval ในตัวดำเนินการ*() ใช้หน่วยความจำของ X4 ผ่าน NRVO
x4 *= x4; // ไม่มีสำเนาของ X4 ที่ทำภายในตัวดำเนินการ*= () แม้ว่าจะกำลังยกกำลังสอง
กลับ x4; // x4 ใช้หน่วยความจำของ y ใน main () ผ่าน nrvo.} int main () {การใช้ namespace boost :: math :: ความแตกต่าง;
คำสั่งที่ไม่ได้ลงนาม constexpr = 5; // อนุพันธ์ลำดับสูงสุดที่จะคำนวณ
อัตโนมัติ const x = make_fvar <double, order> (2.0); // ค้นหาอนุพันธ์ที่ x = 2
อัตโนมัติ const y = fourth_power (x); สำหรับ (ไม่ได้ลงนาม i = 0; i <= order; ++ i)
std :: cout << "y.derivative (" << i << ") =" << y.derivative (i) << std :: endl; กลับ 0;
}/*เอาท์พุท: y.derivative (0) = 16y.derivative (1) = 32y.derivative (2) = 48y.derivative (3) = 48y.derivative (4) = 24y.derivative (5) = 0*////ด้านบนคำนวณ
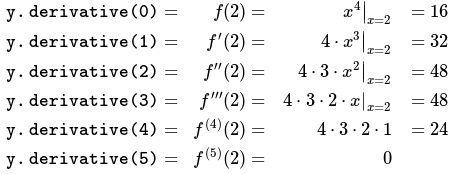
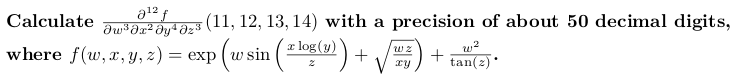
#include <boost/math/difference/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <iostream> การใช้ namespace boost :: math :: difference; tymplate <typename w, typename x, typename y typename z>
โปรโมต <w, x, y, z> f (const w & w, const x & x, const y & y, const z & z) {การใช้ namespace std;
ส่งคืน exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {ใช้ float50 = boost :: multiprecision :: cpp_bin_float_50; Constexpr NW ที่ไม่ได้ลงชื่อ = 3; // คำสั่งสูงสุดของอนุพันธ์เพื่อคำนวณสำหรับ w
constexpr nx ที่ไม่ได้ลงชื่อ = 2; // คำสั่งสูงสุดของอนุพันธ์เพื่อคำนวณสำหรับ x
Constexpr NY ที่ไม่ได้ลงชื่อ = 4; // คำสั่งสูงสุดของอนุพันธ์เพื่อคำนวณสำหรับ y
Constexpr NZ ที่ไม่ได้ลงนาม = 3; // คำสั่งสูงสุดของอนุพันธ์เพื่อคำนวณสำหรับ z
// ประกาศตัวแปรอิสระ 4 ตัวเข้าด้วยกันเป็น std :: tuple
ตัวแปร const อัตโนมัติ = make_ftuple <float50, nw, nx, ny, nz> (11, 12, 13, 14); อัตโนมัติ const & w = std :: get <0> (ตัวแปร); // อนุพันธ์ของ NW ที่ w = 11
อัตโนมัติ const & x = std :: get <1> (ตัวแปร); // สูงสุด NX อนุพันธ์ที่ x = 12
อัตโนมัติ const & y = std :: get <2> (ตัวแปร); // ถึงอนุพันธ์ NY ที่ y = 13
อัตโนมัติ const & z = std :: get <3> (ตัวแปร); // ถึงอนุพันธ์ของนิวซีแลนด์ที่ z = 14
อัตโนมัติ const v = f (w, x, y, z); // คำนวณจากความแตกต่างของสัญลักษณ์ Mathematica
คำตอบ Float50 const ("1976.3196007477977777779881875290418720908121189218755");
std :: cout << std :: setprecision (std :: numeric_limits <float50> :: digits10)
<< "Mathematica:" << คำตอบ << 'n' << "autodiff:" << v.derivative (NW, NX, NY, NZ) << 'n' << std :: setPrecision (3)
<< "ข้อผิดพลาดสัมพัทธ์:" << (V.Derivative (NW, NX, NY, NZ) / คำตอบ - 1) << 'N'; กลับ 0;
}/*เอาท์พุท: Mathematica: 1976.31960074777771777798818752904187209081211892188881821212121212121218181818181818181818181818818212182 #include <boost/math/difference/autodiff.hpp> #include <iostream> การใช้ namespace boost :: math :: cold; https://en.wikipedia.org/wiki/greeks_(finance)#formulas_for_european_option_greeks// มาตรฐานการแจกแจงแบบสะสมปกติ
x phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x);
} enum คลาส cp {call, put}; // สมมติว่าอัตราการจ่ายเงินปันผลประจำปีเป็นศูนย์ (q = 0) .template <ราคา typename, typename sigma, typename tau, typename rate>
โปรโมต <ราคา, ซิกมา, เอกภาพ, อัตรา> black_scholes_option_price (CP CP, double k,
ราคา const & s
Sigma Const & Sigma
Tau Const & Tau
ให้คะแนน const & r) {การใช้เนมสเปซ std;
อัตโนมัติ const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (tau)); อัตโนมัติ const d2 = (log (s / k) + (r - sigma * sigma / 2) * tau) / (sigma * sqrt (tau)); สวิตช์ (cp) {case cp :: call: return s * phi (d1)-exp (-r * tau) * k * phi (d2); case cp :: put: return exp (-r * tau) * k * phi (-d2)-s * phi (-d1);
-
} int main () {double const k = 100.0; // ราคานัดหยุดงาน
อัตโนมัติ const s = make_fvar <double, 2> (105); // ราคาหุ้น
สอง const sigma = 5; // ความผันผวน
double const tau = 30.0 / 365; // ถึงเวลาหมดอายุในปีที่ผ่านมา (30 วัน)
double const r = 1.25 / 100; // อัตราดอกเบี้ย
auto const call_price = black_scholes_option_price (cp :: call, k, s, sigma, tau, r); auto const put_price = black_scholes_option_price (cp :: put, k, s, sigma, tau, r);
std :: cout << "Black-Scholes Call Price =" << call_price.derivative (0) << 'n' << "Black-Scholes วางราคา =" << put_price.derivative (0) << 'n' << "โทรหา delta =" << call_price.derivative (1) << 'n' << "ใส่ delta =" << put_price.derivative (1) << 'n' << "โทร gamma =" << call_price .Derivative (2) << 'n' << "ใส่ gamma =" << put_price.derivative (2) << 'n'; กลับ 0;
}/*เอาท์พุท: Black-Scholes Call ราคา = 56.5136black-Scholes วางราคา = 51.4109CALL Delta = 0.773818put Delta = -0.226182CALL GAMMA = 0.00199852 BUT GAMMA = 0.00199852ดูตัวอย่าง/black_scholes.cpp สำหรับรายการที่ใหญ่กว่าของตัวเลือกที่คำนวณโดยอัตโนมัติ
ตัวอย่างข้างต้นแสดงให้เห็นถึงข้อดีบางประการของการใช้ Autodiff:
การกำจัดความซ้ำซ้อนของรหัส การมีอยู่ของฟังก์ชันแยก ต่างหาก ในการคำนวณอนุพันธ์เป็นรูปแบบของการซ้ำซ้อนของรหัสโดยมีหนี้สินทั้งหมดที่มาพร้อมกับมัน:
การเปลี่ยนแปลงฟังก์ชั่นหนึ่งต้องการ การ เปลี่ยนแปลงเพิ่มเติมกับฟังก์ชั่นอื่น ๆ ในตัวอย่างที่ 3 ด้านบนให้พิจารณาว่าฐานรหัสด้านบนจะใหญ่ขึ้นและขึ้นอยู่กับการทำงานของฟังก์ชันแยกต่างหากสำหรับค่ากรีกแต่ละค่า
การพึ่งพาฟังก์ชั่นอนุพันธ์เพื่อจุดประสงค์ที่แตกต่างกันจะแตกหักเมื่อมีการเปลี่ยนแปลงกับฟังก์ชั่นดั้งเดิม สิ่งที่ไม่จำเป็นต้องมีอยู่ไม่สามารถทำลายได้
โค้ด bloat ลดความสมบูรณ์ของแนวคิด การควบคุมวิวัฒนาการของรหัสนั้นง่ายขึ้น/ปลอดภัยกว่าเมื่อฐานรหัสมีขนาดเล็กลงและสามารถจับได้อย่างสังหรณ์ใจ
ความแม่นยำของอนุพันธ์ผ่านวิธีการแตกต่างกันอย่าง จำกัด วิธีการที่แตกต่างกันอย่าง จำกัด ด้วยเครื่องประดับเดียวมักจะมีตัวแปรฟรี Δx ที่ต้องเลือกอย่างรอบคอบสำหรับแต่ละแอปพลิเคชัน ถ้า Δx มีขนาดเล็กเกินไปข้อผิดพลาดเชิงตัวเลขจะมีขนาดใหญ่ หาก Δx มีขนาดใหญ่เกินไปข้อผิดพลาดทางคณิตศาสตร์จะมีขนาดใหญ่ ด้วย Autodiff ไม่มีตัวแปรฟรีที่จะตั้งค่าและความแม่นยำของคำตอบโดยทั่วไปจะดีกว่าวิธีการแตกต่างที่ จำกัด แม้จะมีตัวเลือกที่ดีที่สุดของ Δx
รายละเอียดเพิ่มเติมอยู่ในคู่มืออัตโนมัติ
แจกจ่ายภายใต้ใบอนุญาตซอฟต์แวร์ Boost เวอร์ชัน 1.0
ส่วนหัวเท่านั้น
ปรับให้เหมาะสมสำหรับ C ++ 17 นอกจากนี้ยังรวบรวมและทดสอบด้วย C ++ 11, C ++ 14 และเสนอมาตรฐาน C ++ 20
หน่วยความจำทั้งหมดได้รับการจัดสรรบนสแต็ก
| ชื่อ | วัตถุประสงค์ |
|---|---|
doc | เอกสาร |
example | ตัวอย่าง |
include | ส่วนหัว |
test | การทดสอบหน่วย |
รายงานข้อบกพร่อง: อย่าลืมพูดถึงรุ่น Boost แพลตฟอร์มและคอมไพเลอร์ที่คุณใช้ ตัวอย่างรหัสขนาดเล็กที่รวบรวมได้เพื่อทำซ้ำปัญหาก็ดีเช่นกัน
ส่งแพตช์ของคุณเป็นคำขอดึงกับสาขาพัฒนา โปรดทราบว่าโดยการส่งแพตช์คุณตกลงที่จะอนุญาตการแก้ไขของคุณภายใต้ใบอนุญาตซอฟต์แวร์ Boost เวอร์ชัน 1.0