
และงาน Fiber ใน React และงาน Fiber ต่างๆ มีลำดับความสำคัญที่แตกต่างกัน React จำเป็นต้องประมวลผลงานที่มีลำดับความสำคัญสูงก่อน ตัวอย่างเช่น การคลิกและการป้อนข้อมูลของผู้ใช้เป็นงานที่มีลำดับความสำคัญสูง เนื่องจากการดำเนินงานของผู้ใช้หวังว่าจะมีผลทันที เพื่อปรับปรุงประสบการณ์ผู้ใช้ ตัวอย่างเช่น ลำดับความสำคัญของกิจกรรมแอนิเมชั่นจะต้องต่ำกว่านี้ หลังจากที่งานที่มีลำดับความสำคัญสูงใหม่เข้าสู่คิว React จะต้องประมวลผลก่อน
ในการจัดเก็บงานเหล่านี้ มีกลุ่มงานสองกลุ่มใน React
// งานจะถูกเก็บไว้ในฮีปขั้นต่ำ var TaskQueue = []; var timerQueue = [];
taskQueue และ timerQueue เป็นทั้งอาร์เรย์ งานเก็บก่อนหน้านี้ที่จะดำเนินการทันที ในขณะที่งานหลังเก็บงานที่อาจล่าช้าได้
var newTask = {
id: taskIdCounter++, // ทำเครื่องหมายรหัสงาน
callback, // ฟังก์ชันการเรียกกลับ PriorityLevel, // ลำดับความสำคัญของงาน startTime, // เวลาเริ่มต้นงาน, จุดเวลา expirationTime, // เวลาหมดอายุ, จุดเวลา sortIndex: -1, // การเรียงลำดับงาน, ค่ามาจากเวลาหมดอายุ ดังนั้น ค่า ยิ่งค่าน้อยลง ลำดับความสำคัญก็จะยิ่งสูงขึ้น} เมื่องานใหม่เข้ามา React จะใช้ currentTime เพื่อบันทึกเวลาปัจจุบันก่อน (Performance.now() หรือ Date.now()) พารามิเตอร์ล่าช้า จากนั้นงานจะเริ่มเวลาดำเนินการ startTime = currentTime + Delay;. ถัดไป หากกำหนด startTime > currentTime ไว้ จะพิสูจน์ว่างานสามารถเลื่อนออกไปได้ จากนั้นงานจะเข้าสู่ timerQueue ไม่เช่นนั้นจะเข้าสู่ TaskQueue
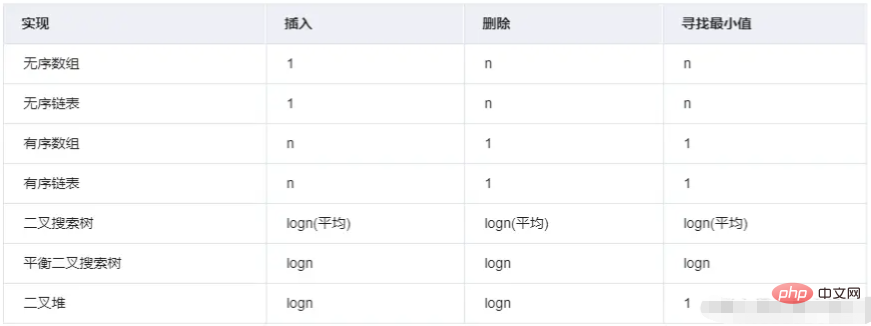
React ค้นหางานที่มีลำดับความสำคัญสูงสุดได้อย่างไร ใช้ TaskQueue เป็นตัวอย่าง มันเป็นกลุ่มงานแบบไดนามิก (คิวงาน) และแบบฟอร์มข้อมูลเป็นอาร์เรย์ แน่นอน คุณสามารถเรียงลำดับตามลำดับความสำคัญได้ นั่นคือ Array.sort เมื่อมีการเพิ่มงานใหม่ลงในคิว งานนั้นจะถูกเรียงลำดับก่อน จากนั้นจึงพบและดำเนินการงานที่มีลำดับความสำคัญสูงสุด แต่ความซับซ้อนของเวลาโดยเฉลี่ยของ Array.sort คือ O(nlogn) ซึ่งไม่ใช่วิธีแก้ปัญหาที่ดีที่สุด
SortIndex ใช้สำหรับการเรียงลำดับในงาน newTask ของ TaskQueue ค่านี้นำมาจากเวลาหมดอายุ ซึ่งหมายความว่ายิ่งงานมีลำดับความสำคัญสูงเท่าไรก็ยิ่งต้องเข้าใจและดำเนินการมากขึ้นเท่านั้น ดังนั้นเวลาหมดอายุก็จะน้อยลง ยิ่งมีลำดับความสำคัญสูง เวลาหมดอายุก็จะยิ่งน้อยลงเท่านั้น sortIndex ก็จะยิ่งน้อยลงตามไปด้วย อันที่จริง นี่คือคิวลำดับความสำคัญ
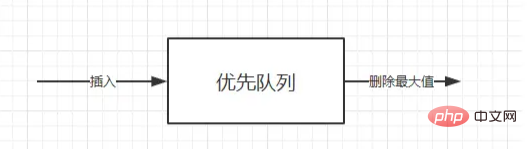
ลำดับความสำคัญยังเป็นคิวชนิดหนึ่ง ( ประการแรก มันคือคิว และประการที่สอง เข้ามาก่อน ออกก่อน ) ข้อแตกต่างเพียงอย่างเดียวคือลำดับการถอนคิวของคิวลำดับความสำคัญจะขึ้นอยู่กับลำดับความสำคัญในบางกรณี คุณอาจต้องค้นหาองค์ประกอบขั้นต่ำหรือสูงสุดในชุดองค์ประกอบที่สามารถดำเนินการได้โดยใช้ลำดับความสำคัญของคิว ADT การลบการดำเนินการค่าสูงสุด (การส่งคืนและการลบองค์ประกอบขั้นต่ำ)
หากองค์ประกอบที่มีค่าคีย์น้อยที่สุดมีลำดับความสำคัญสูงสุด คิวลำดับความสำคัญนี้เรียกว่าคิวลำดับความสำคัญจากน้อยไปหามาก (นั่นคือ องค์ประกอบที่เล็กที่สุดจะถูกลบออกก่อนเสมอ) ในทำนองเดียวกัน หากองค์ประกอบที่มีค่าคีย์ที่ใหญ่ที่สุดมีลำดับความสำคัญสูงสุด คิวลำดับความสำคัญประเภทนี้จะเรียกว่าคิวลำดับความสำคัญจากมากไปน้อย (นั่นคือ องค์ประกอบที่ใหญ่ที่สุดจะถูกลบออกก่อนเสมอ) เนื่องจากทั้งสองประเภทนี้มีความสมมาตร คุณเพียงต้องการเท่านั้น เพื่อมุ่งเน้นไปที่ประเภทใดประเภทหนึ่งเช่นการเรียงลำดับลำดับความสำคัญ
เช่น ตอนที่เราซื้อตั๋ว เราก็เข้าคิวกันหมดแล้วใครก็ตามที่อยู่ข้างหน้าคิวก็จะซื้อตั๋วก่อน . ด้านหน้า.
ฮีปขั้นต่ำ (ฮีปรูทเล็ก ฮีปบนเล็ก...) ถูกใช้ใน React เพื่อให้ได้ฟังก์ชันนี้ นั่นคือการเปลี่ยน TaskQueue ให้เป็นฮีปขั้นต่ำ จากนั้นนำงานอันดับต้นๆ ออกมาเพื่อดำเนินการ ฮีป TaskQueue และคงไว้เป็นโครงสร้างข้อมูลฮีปขั้นต่ำ เมื่อแทรกงานใหม่ลงใน TaskQueue งานนั้นจะต้องถูกฮีปด้วยและคงเป็นฮีปขั้นต่ำเสมอ
: ในบางจุดฮีปเรียกว่าคิวลำดับความสำคัญ (ไม่ถูกต้อง) ประการแรกคือคิวและมีลักษณะเป็นคิวคือ " เข้าก่อน ออกก่อน " . ประการที่สอง องค์ประกอบในคิวนี้มีลำดับความสำคัญ และองค์ประกอบที่มีลำดับความสำคัญสูงกว่าจะได้รับการจัดอันดับเป็นอันดับแรก
พูดให้ถูกคือฮีปคือวิธีหนึ่งในการดำเนินการคิวลำดับความสำคัญ แน่นอนว่าการจัดลำดับความสำคัญสามารถนำไปใช้ในรูปแบบอื่นได้เช่นกัน
เรากล่าวไว้ก่อนหน้านี้ว่าการเรียงลำดับฮีปนั้นเป็นการเรียงลำดับที่ไม่เสถียร แต่ TaskQueue หวังว่ากระบวนการนี้จะเสถียร กล่าวคือ หากเป็นไปได้ที่เวลาหมดอายุของสองงานจะเท่ากัน ก็ขึ้นอยู่กับว่าใครเข้ามา อันดับแรก กลุ่มงานคือค่าของ id ของ newTask ทุกครั้งที่มีงานใหม่ id จะเพิ่มขึ้น 1
ฟังก์ชั่นเปรียบเทียบ (a, b) {
// เปรียบเทียบดัชนีการเรียงลำดับก่อน จากนั้นจึงระบุรหัสงาน
const diff = a.sortIndex - b.sortIndex;
กลับความแตกต่าง !== 0 ? diff : a.id - b.id;
} ก่อนที่จะทำความเข้าใจฮีปขั้นต่ำ เรามาทบทวนความรู้พื้นฐานกันก่อน
หมายถึงต้นไม้ที่ได้รับคำสั่งซึ่งมีระดับของโหนดในต้นไม้ไม่เกิน 2 เป็นต้นไม้ที่ง่ายที่สุดและสำคัญที่สุด
คือ binary tree ซึ่งโหนดทั้งหมดในแต่ละระดับจะมีโหนดย่อยสองโหนด ยกเว้นระดับสุดท้ายที่ไม่มีโหนดย่อย
จากมุมมองแบบกราฟิก ต้นไม้ไบนารี่แบบเต็มจะดูเหมือนสามเหลี่ยม
หากจำนวนระดับของต้นไม้ไบนารี่คือ K และจำนวนโหนดทั้งหมดคือ (2^k) -1 แสดงว่าต้นไม้ไบนารี่เต็ม
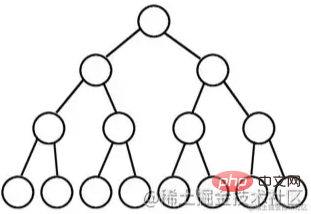
ต้นไม้ไบนารีเต็ม หมายถึง "ลูกสาวมีทั้งสองด้าน" และสมบูรณ์แบบมาก จึงเรียกว่าต้นไม้ไบนารีเต็ม
ไม่รวมโหนดใบ ระดับของโหนดทั้งหมดคือ 2 กล่าวอีกนัยหนึ่ง ระดับของโหนดทั้งหมดสามารถเป็น 0 หรือ 2 เท่านั้น
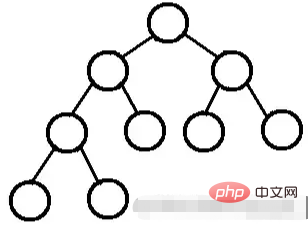
ต้นไม้ไบนารี่ที่สมบูรณ์แบบไม่มีลูกหรือลูกทั้งสองคน
ข้อความต้นฉบับภาษาอังกฤษของ Full Binary Tree:
Full Binary Tree (FBT) คือต้นไม้ที่ทุกโหนดนอกเหนือจากใบไม้มีลูกสองคน
ข้อความต้นฉบับภาษาอังกฤษของต้นไม้ไบนารี่ที่สมบูรณ์แบบ:
A Perfect Binary Tree (PBT) คือต้นไม้ที่มีโหนดใบทั้งหมดที่มีความลึกเท่ากัน โหนดภายในทั้งหมดมีระดับ 2
หนังสือต่างประเทศทั้งหมดอ้างถึงหนังสือเรียนที่แปลเร็วที่สุดบนต้นไม้ไบนารี่แบบเต็มและต้นไม้ไบนารี่ที่สมบูรณ์แบบ แต่บทความที่แปลเร็วที่สุดนั้นแปลผิด ตอนนี้ในประเทศจีนเราทำผิดได้ก็ต่อเมื่อมันผิดเท่านั้น (ใครๆ ก็ผิด แล้วคนผิดก็ถูกด้วย เช่น ผู้ทำการแนะนำชักชวนสมาชิกรัฐสภา...) หากคุณต้องการหารือเกี่ยวกับแนวคิดทั้งสองนี้กับเพื่อนชาวต่างชาติคุณควรให้ความสนใจ
Binary Tree (CBT) คือ binary tree ซึ่งทุกระดับยกเว้นระดับสุดท้ายจะถูกเติมเต็ม และโหนดทั้งหมดจะอยู่ทางซ้ายสุดที่เป็นไป
ได้ tree จากบนลงล่างและจากซ้ายไปขวา หากโหนดหมายเลข i (1≤i≤n) อยู่ในไบนารีทรีโดยมีโหนดหมายเลข i อยู่ในไบนารีทรีแบบเต็ม หากตำแหน่งเท่ากัน ต้นไม้ไบนารีก็จะเป็น เรียกว่าต้นไม้ไบนารีสมบูรณ์
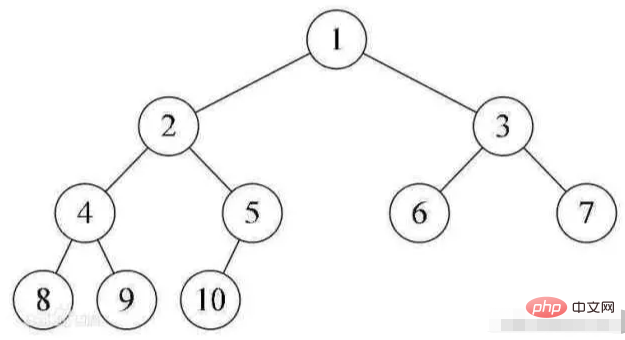
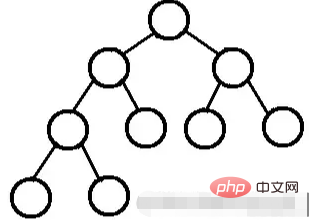
ฮีปจะเป็นไปตามคุณสมบัติต่อไปนี้เสมอ:
ก่อนเสมอ รูตฮีปขนาดเล็ก ในแผนผังไบนารี่ที่สมบูรณ์ โหนดทั้งหมดมีขนาดใหญ่กว่า (หรือเล็กกว่า) โหนดย่อย ดังนั้นจึงมีสองสถานการณ์ที่นี่ คือ ฮีปสูงสุดและฮีปขั้นต่ำ
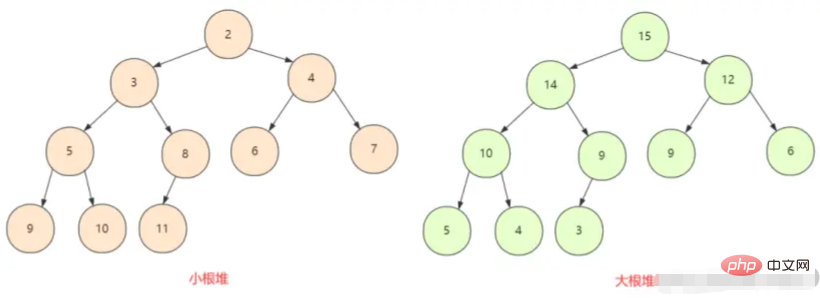
ฮีปมักจะเป็นอาร์เรย์ของอ็อบเจ็กต์ที่สามารถดูได้เป็น แผนผังไบนารีที่ สมบูรณ์ แน่นอนว่าไบนารีทรีสามารถแสดงด้วยอาร์เรย์ได้เช่นกัน
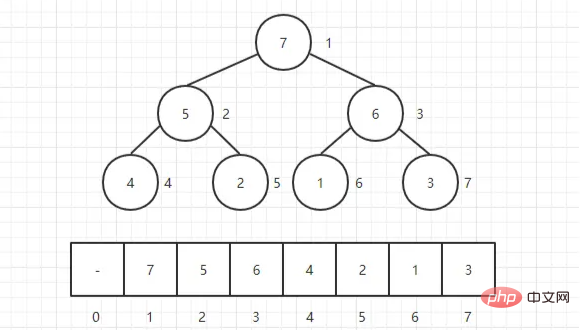
คือการสร้างฮีปก่อนแล้วค่อยปรับเปลี่ยน
สำหรับแผนผังไบนารี (การแสดงอาร์เรย์) เราจะปรับจากล่างขึ้นบน โดยเริ่มจาก "โหนดที่ไม่ใช่ลีฟแรก" และปรับไปข้างหน้า กฎสำหรับการปรับเปลี่ยนมีดังนี้:
การสร้างฮีปคือ O(n ) กระบวนการความซับซ้อนของเวลา
1 เริ่มจากโหนดที่ไม่ใช่ลีฟแรกเพื่อตัดสินการสลับลง (shiftDown) เพื่อให้โหนดปัจจุบันและลูกสามารถรักษาคุณสมบัติฮีปได้
2 อย่างไรก็ตาม การแทนที่โหนดธรรมดาอาจไม่เป็นปัญหา หากการแลกเปลี่ยนทำลายคุณสมบัติโครงสร้างฮีป ของเด็กแล้วจะต้องกด ShiftDown โหนดที่สลับอีกครั้งจนกว่าจะหยุด
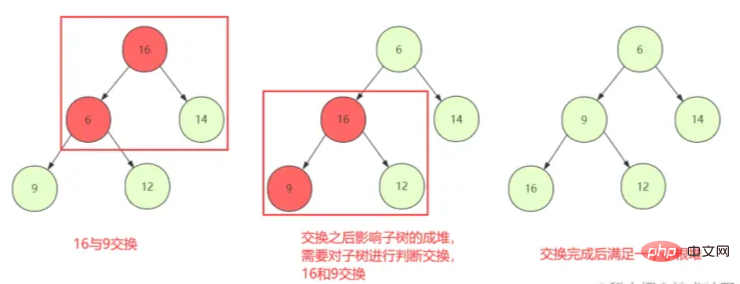
ฮีป
ทำลายโครงสร้างฮีปได้
1. ดังนั้น ให้ใส่องค์ประกอบสุดท้ายก่อน ด้วยวิธีนี้ คุณเพียงแค่ต้องตัดสินการสลับกะ (shiftDown) แต่คุณต้องทราบว่าขนาดของฮีปทั้งหมดมีการเปลี่ยนแปลงในขณะนี้ เราจะไม่ใช้ตำแหน่งที่ถูกละทิ้งอย่างมีเหตุผล ดังนั้นเราจึงจำเป็นต้องรวมฮีปด้วย พารามิเตอร์ขนาดเมื่อออกแบบฟังก์ชัน
② ทำซ้ำการดำเนินการข้างต้นจนกว่าจะได้รับองค์ประกอบทั้งหมดในฮีป
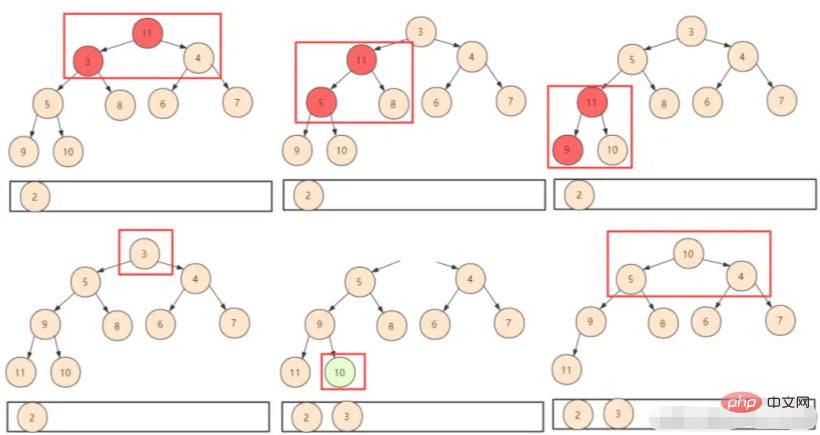
ในแง่ของการวิเคราะห์ความซับซ้อนของอัลกอริธึมฮีป ความซับซ้อนของเวลาในการสร้างฮีปก่อนหน้านี้คือ O(n) แต่ละครั้งที่ด้านบนสุดของฮีปถูกลบแล้วสลับลง จำนวนของแต่ละฮีปจะถูกบันทึกไว้ ด้วยวิธีนี้ ความซับซ้อนคือ O(nlogn) และความซับซ้อนของเวลาทั้งหมดคือ O(n)+O(nlogn)=O(nlogn)
Heap เหมาะสำหรับการรักษามูลค่าสูงสุดของคอลเลกชัน
หลังจากที่องค์ประกอบถูกดึงออกจากฮีป ค่าใช้จ่ายในการปรับใหม่เพื่อให้ได้องค์ประกอบบนสุดของฮีป (นั่นคือค่าสูงสุดอันดับสอง) จะค่อนข้างต่ำ เนื่องจากหลังจากองค์ประกอบถูกดึงออกมา ฮีปจะเป็นแบบกึ่ง -ผลิตภัณฑ์สำเร็จรูป และค่าสูงสุดอันดับสองได้มาจากผลิตภัณฑ์กึ่งสำเร็จรูป แน่นอนว่าต้นทุนค่อนข้างต่ำ และความซับซ้อนของเวลาคือ O(logn) แต่ถ้ามีการสำรวจหนึ่งครั้งเพื่อค้นหาค่าสูงสุดอันดับสอง ความซับซ้อนของเวลาคือ O(n)
เขียนด้วย Javascript ES6
คลาสฮีป {
ตัวสร้าง (ข้อมูลคอมพ์) {
this.data = ข้อมูล ? ข้อมูล : [];
// กฎการเปรียบเทียบ: ยืดหยุ่นมากขึ้นคุณสามารถเปรียบเทียบค่าหรือวัตถุได้ this.compartor = comp ? comp : (ab) => ab;
// ปรับเป็นฮีป (คิวลำดับความสำคัญ)
นี้.heapify();
-
สร้างกอง() {
if(this.size() <= 1) กลับ;
// เริ่มการปรับจากโหนดที่ไม่ใช่ลีฟแรก หรือคุณสามารถปรับจากองค์ประกอบสุดท้ายสำหรับ(let i=Math.floor((this.size()-2)/2); i>=0; i-- ) {
//ปรับฮีป การปรับด้านล่างสามารถทำได้โดยใช้การเรียกซ้ำ ในที่นี้ การวนซ้ำจะใช้เพื่อใช้งาน this.shiftDown(i);
-
-
// ปรับ shiftDown ลง (i) {
ปล่อยให้ซ้าย = 2*i +1;
ให้ขวา = 2*i +2;
ให้ len = this.size();
ในขณะที่ (ฉัน <เลน) {
ให้ findIndex = i;
//ลูกซ้าย "ใหญ่กว่า"
ถ้า (ซ้าย < len && this.compartor (this.data [ซ้าย], this.data [findIndex]) < 0) {
findIndex = ซ้าย;
-
// ลูกที่ถูกต้องคือ "ใหญ่กว่า"
ถ้า (ขวา < len && this.compartor (this.data [ขวา], this.data [findIndex]) < 0) {
findIndex = ขวา;
-
ถ้า (i !== findIndex) {
//แลกเปลี่ยนโหนดปัจจุบันด้วยค่าที่มากขึ้น [this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
// หลังจากปรับเลเยอร์นี้แล้ว อาจส่งผลต่อคุณลักษณะของฮีปของเลเยอร์ด้านล่าง ดังนั้นให้ปรับเลเยอร์ด้านล่างต่อไป (การใช้งานซ้ำหรือเรียกซ้ำ)
ฉัน = findIndex;
ซ้าย = 2*i +1;
ขวา = 2*i +2;
-
อื่น {
// หากไม่ต้องการปรับให้กระโดดออก (ต้องกระโดดออก ไม่เช่นนั้นวงจะสิ้นสุดไม่ได้)
หยุดพัก;
-
-
-
// ปรับ shiftUp ขึ้น (i) {
// ค้นหาตัวห้อยของ parent ให้ parentIndex = Math.floor((i-1)/2);
// ปรับค่าสูงสุดเป็น 0
ในขณะที่ (parentIndex >=0 ) {
ให้ findIndex = i;
ถ้า (this.compartor (this.data [parentIndex], this.data [findIndex]) > 0) {
findIndex = parentIndex;
-
ถ้า (findIndex !== i) {
[this.data[i], this.data[findIndex]] = [this.data[findIndex], this.data[i]];
ฉัน = findIndex;
parentIndex = Math.floor((i-1)/2);
-
อื่น {
หยุดพัก;
-
-
-
// รับจำนวนองค์ประกอบทั้งหมดในขนาดฮีป(){
กลับ this.data.length;
-
// รับองค์ประกอบแรกของฮีป peek(){
if(!this.size()) กลับ null;
กลับ this.data[0];
-
//เพิ่มองค์ประกอบให้กับฮีปพุช(x){
นี้.data.push(x);
this.shiftUp(this.data.length-1);
-
// ป๊อปองค์ประกอบแรกจากฮีปป๊อป () {
if(!this.size()) กลับ null;
ให้ความละเอียด = this.data[0];
ถ้า(this.size() == 1) {
this.data.pop();
-
อื่น {
this.data[0] = this.data[this.data.length-1];
this.data.length = this.data.length-1;
นี้.shiftDown(0);
-
ส่งคืนความละเอียด;
-
} ให้ arr = [2,9,8,6,3,10,5,7,4,1];
ให้คอมพ์ = (a, b) => ab;
ให้ heap = Heap ใหม่ (arr, comp);
ให้ความละเอียด = [];
ในขณะที่ (ฮีป. ขนาด ()) {
res.push(ฮีป.ป๊อป());
-
console.log(res); องค์ประกอบใน arr ยังสามารถเป็นวัตถุได้
แพ็คเกจไดเร็กทอรี/ตัวกำหนดเวลาในซอร์สโค้ด React เป็นโค้ดที่เกี่ยวข้องกับโมดูลการกำหนดเวลางานของ React
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src/Scheduler.js
https://github.com/facebook/react/blob/17.0.2/packages/scheduler/src /SchedulerMinHeap.js
-
* ลิขสิทธิ์ (c) Facebook, Inc. และบริษัทในเครือ
-
* ซอร์สโค้ดนี้ได้รับอนุญาตภายใต้ใบอนุญาต MIT ที่พบใน
* ไฟล์ลิขสิทธิ์ในไดเร็กทอรีรากของแผนผังต้นทางนี้
-
* @flow เข้มงวด
-
พิมพ์ Heap = Array<Node>;
พิมพ์โหนด = {|
รหัส: หมายเลข
sortIndex: ตัวเลข,
-
ฟังก์ชั่นการส่งออกผลักดัน (ฮีป: ฮีป, โหนด: โหนด): เป็นโมฆะ {
ดัชนี const = heap.length;
ฮีป.พุช(โหนด);
siftUp(ฮีป, โหนด, ดัชนี);
-
ฟังก์ชั่นการส่งออกดู (ฮีป: ฮีป): โหนด | .
const ก่อน = ฮีป [0];
กลับก่อน === ไม่ได้กำหนด ? null : ก่อน;
-
ฟังก์ชั่นการส่งออกป๊อป (ฮีป: ฮีป): โหนด | .
const ก่อน = ฮีป [0];
ถ้า (แรก !== ไม่ได้กำหนด) {
const สุดท้าย = heap.pop();
ถ้า (สุดท้าย !== ก่อน) {
ฮีป[0] = สุดท้าย;
ร่อนลง (ฮีป, สุดท้าย, 0);
-
กลับมาก่อน;
} อื่น {
กลับเป็นโมฆะ;
-
-
ฟังก์ชั่น siftUp (ฮีป, โหนด, i) {
ให้ดัชนี = i;
ในขณะที่ (จริง) {
const parentIndex = (ดัชนี - 1) >>> 1;
const parent = ฮีป [parentIndex];
ถ้า (พาเรนต์ !== ไม่ได้กำหนด && เปรียบเทียบ (พาเรนต์, โหนด) > 0) {
// ตำแหน่งแม่มีขนาดใหญ่กว่า
ฮีป [parentIndex] = โหนด;
ฮีป [ดัชนี] = ผู้ปกครอง;
ดัชนี = parentIndex;
} อื่น {
// ผู้ปกครองมีขนาดเล็กกว่า
กลับ;
-
-
-
ฟังก์ชั่น siftDown (ฮีป, โหนด, i) {
ให้ดัชนี = i;
ความยาว const = heap.length;
ในขณะที่ (ดัชนี <ความยาว) {
const leftIndex = (ดัชนี + 1) * 2 - 1;
const ซ้าย = ฮีป [leftIndex];
const rightIndex = ดัชนีซ้าย + 1;
const ขวา = ฮีป [rightIndex];
// หากโหนดซ้ายหรือขวาเล็กกว่า ให้สลับกับโหนดที่เล็กกว่า
ถ้า (ซ้าย !== ไม่ได้กำหนด && เปรียบเทียบ (ซ้าย, โหนด) < 0) {
ถ้า (ขวา !== ไม่ได้กำหนด && เปรียบเทียบ (ขวา, ซ้าย) < 0) {
ฮีป [ดัชนี] = ขวา;
ฮีป [rightIndex] = โหนด;
ดัชนี = ดัชนีขวา;
} อื่น {
ฮีป [ดัชนี] = ซ้าย;
ฮีป [leftIndex] = โหนด;
ดัชนี = ดัชนีซ้าย;
-
} อื่น ๆ ถ้า (ขวา !== ไม่ได้กำหนด && เปรียบเทียบ (ขวา โหนด) < 0) {
ฮีป [ดัชนี] = ขวา;
ฮีป [rightIndex] = โหนด;
ดัชนี = ดัชนีขวา;
} อื่น {
// ไม่มีลูกคนไหนเล็กลง
กลับ;
-
-
-
ฟังก์ชั่นเปรียบเทียบ (a, b) {
// เปรียบเทียบดัชนีการเรียงลำดับก่อน จากนั้นจึงระบุรหัสงาน
const diff = a.sortIndex - b.sortIndex;
กลับความแตกต่าง !== 0 ? diff : a.id - b.id;
} ฮีปขั้นต่ำที่เรานำไปใช้นั้นแตกต่างจากการใช้งานใน React เล็กน้อย แต่แนวคิดก็เหมือนกัน มีเพียงโค้ดเท่านั้นที่เขียนแตกต่างออกไป
การกำหนดเวลางานใน React ถูกนำมาใช้โดยใช้ฮีปขั้นต่ำ หากเรามีความเข้าใจเกี่ยวกับฮีปขั้นต่ำมาก่อน เราจะเรียนรู้เนื้อหานี้ได้เร็วขึ้น โดยส่วนตัวผมคิดว่าการสั่งสมความรู้ตั้งแต่เนิ่นๆ นั้นสำคัญขนาดไหน แต่กระบวนการนี้อาจจะน่าเบื่อ ในเวลานี้ คุณคิดว่าคุณรู้จักอัลกอริธึมบางอย่างแล้วหรือยัง อันที่จริง อัลกอริธึมเหล่านี้เป็นระดับเริ่มต้นและคุณยังไม่ได้เริ่มเลยด้วยซ้ำ เนื่องจากในสถานการณ์การกำหนดเวลางานของ React ข้อกำหนดที่ต้องนำไปใช้มีความชัดเจนมาก โครงสร้างข้อมูลและอัลกอริธึมที่จะใช้ก็มีความชัดเจนเช่นกัน ในสถานการณ์จริงบางสถานการณ์ เรารู้ข้อกำหนดเฉพาะ แต่เราไม่รู้ว่าจะใช้ผลลัพธ์และอัลกอริธึมข้อมูลใด เราจำเป็นต้องสรุปข้อกำหนดและออกแบบโครงสร้างข้อมูลและอัลกอริธึมเฉพาะตามแบบจำลองข้อมูลเชิงนามธรรม สิ่งเหล่านี้คือประเด็นสำคัญ .