ปัญหาบีเวอร์แสนยุ่ง ซึ่งเป็นปัญหาวิทยาการคอมพิวเตอร์ที่กินเวลานานถึงสี่สิบปี ในที่สุดกลุ่มมือสมัครเล่นก็ได้รับการแก้ไขแล้ว! การพัฒนาที่ก้าวล้ำนี้ไม่เพียงแต่สร้างความตกตะลึงให้กับชุมชนวิชาการเท่านั้น แต่ยังได้รับการยอมรับจากนักคณิตศาสตร์ชื่อดังอย่าง Terence Tao และได้รับการยกย่องว่าเป็นการพัฒนาที่สำคัญที่สุดในสาขานี้นับตั้งแต่ปี 1983 ด้วยการใช้ตัวช่วยพิสูจน์ Coq พวกเขายืนยันได้สำเร็จว่าค่าของหมายเลขบีเวอร์ตัวที่ห้า BB(5) คือ 47,176,870 ซึ่งแสดงให้เห็นถึงศักยภาพที่ยอดเยี่ยมของการพิสูจน์โดยใช้ซอฟต์แวร์ช่วยในการแก้ปัญหาทางคณิตศาสตร์ที่ซับซ้อน และยังให้ข้อมูลเชิงลึกเกี่ยวกับพฤติกรรมของเครื่องจักรทัวริงอีกด้วย และยุติปัญหามุมมองใหม่
ในพื้นที่ลึกลับของวิทยาการคอมพิวเตอร์ ปัญหาอายุสี่สิบปีที่เรียกว่าปัญหาบีเวอร์ยุ่ง เพิ่งได้รับการแก้ไขโดยกลุ่มมือสมัครเล่นได้สำเร็จ ความสำเร็จนี้ไม่เพียงแต่สร้างความฮือฮาในโลกวิชาการเท่านั้น แต่ยังได้รับการยอมรับจากนักคณิตศาสตร์ชื่อดัง เทอเรนซ์ เต๋า ผู้ส่งต่อข่าวบนโซเชียลมีเดีย และเน้นย้ำถึงความสำคัญของผู้ช่วยพิสูจน์อักษรในการวิจัยทางคณิตศาสตร์
นักวิทยาศาสตร์คอมพิวเตอร์ Scott Aaronson ยังได้ชื่นชมการค้นพบนี้ด้วย โดยเชื่อว่าเป็นการพัฒนาที่สำคัญที่สุดในการวิจัยการทำงานของบีเวอร์ที่มีงานยุ่งมาตั้งแต่ปี 1983 ความสำเร็จนี้แสดงให้เห็นถึงความเข้าใจอย่างลึกซึ้งเกี่ยวกับขอบเขตของทฤษฎีการคำนวณ และแสดงให้เห็นถึงศักยภาพของการพิสูจน์โดยใช้ซอฟต์แวร์ช่วยในการแก้ปัญหาทางคณิตศาสตร์ที่ซับซ้อน
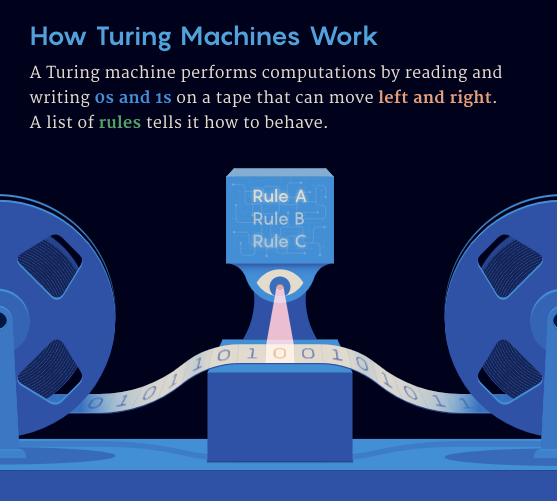
ปัญหาบีเวอร์ที่ยุ่งวุ่นวายเกิดขึ้นเมื่อ 40 ปีที่แล้วในเมืองดอร์ทมุนด์ ประเทศเยอรมนี เมื่อนักวิทยาศาสตร์คอมพิวเตอร์พยายามค้นหาเครื่องจักรทัวริงเฉพาะที่สามารถเขียนเลข 1 ได้มากที่สุดก่อนที่จะหยุด เครื่องจักรทัวริงเป็นแบบจำลองการคำนวณเชิงนามธรรมที่เสนอโดยอลัน ทัวริงในปี 1936 ซึ่งทำการคำนวณบนเทปแม่เหล็กที่มีความยาวเป็นอนันต์โดยการอ่านและเขียน 0 และ 1

หลังจากระบุหมายเลขบีเวอร์ตัวที่สี่ในปี 1974 การค้นหาบีเวอร์ตัวที่ห้าก็กลายเป็นคำถามเปิด ขณะนี้ ชุมชนออนไลน์ที่มีผู้ร่วมให้ข้อมูลมากกว่า 20 รายจากทั่วโลก โดยใช้ซอฟต์แวร์ผู้ช่วยพิสูจน์ชื่อ Coq ได้ยืนยันเรียบร้อยแล้วว่าหมายเลข Busy Beaver หมายเลขที่ห้า BB(5) มีค่าเท่ากับ 47,176,870
ความสำเร็จนี้ไม่เพียงแต่สร้างความตื่นเต้นให้กับชุมชนเท่านั้น แต่ยังกระตุ้นความประหลาดใจของนักวิทยาศาสตร์คอมพิวเตอร์ Damien Woods ซึ่งเปรียบความก้าวหน้ากับความเร็วของ Usain Bolt แม้ว่าการแก้ปัญหานี้อาจไม่สามารถใช้ได้กับสาขาอื่นๆ ของวิทยาการคอมพิวเตอร์โดยตรง แต่สำหรับผู้เข้าร่วม การต่อสู้กับความเป็นไปไม่ได้ทางคณิตศาสตร์ครั้งนี้ถือเป็นรางวัลที่ยิ่งใหญ่ที่สุดในตัวมันเอง
แก่นแท้ของปัญหาบีเวอร์ไม่ว่างอยู่ที่การทำความเข้าใจพฤติกรรมของเครื่องทัวริง โดยเฉพาะประสิทธิภาพในการหยุดปัญหา พฤติกรรมของเครื่องทัวริงถูกกำหนดโดยชุดกฎ ซึ่งสามารถจินตนาการได้เป็นตาราง แต่ละกฎระบุการกระทำที่ควรดำเนินการเมื่อหัวอ่าน/เขียนพบ 0 หรือ 1 ในสถานะเฉพาะ
แม้ว่าเครื่องจักรทัวริงอาจติดอยู่ในลูปไม่สิ้นสุด แต่การพิจารณาว่าเครื่องจักรจะหยุดทำงานหรือไม่นั้นเป็นปัญหาที่ยังไม่ได้รับการแก้ไข นักคณิตศาสตร์ ติบอร์ ราโด ไม่พอใจกับข้อสรุปนี้ จึงได้คิดค้น "เกมบีเวอร์ยุ่ง" เพื่อสำรวจธรรมชาติของปัญหาที่หยุดชะงักโดยการจัดกลุ่มเครื่องจักรทัวริงตามกฎจำนวนที่พวกเขามี
นักวิจัยในยุคแรกๆ เช่น Allen Brady ได้สำรวจปัญหานี้โดยการเขียนโปรแกรมเพื่อจำลองพฤติกรรมของเครื่องจักรทัวริง งานของเขาและการค้นพบของนักวิจัยคนอื่นๆ ได้วางรากฐานสำหรับนักสำรวจรุ่นหลัง
จนถึงปี 2022 Tristan Stérin นักศึกษาระดับบัณฑิตศึกษาได้เปิดตัว Busy Beaver Challenge ซึ่งเป็นโครงการความร่วมมือออนไลน์ที่มุ่งเป้าไปที่การสรุป BB(5) ด้วยวิธีการที่เป็นนวัตกรรมใหม่และความช่วยเหลือจากผู้ช่วยพิสูจน์ Coq ในที่สุดทีมก็ประสบความสำเร็จในการค้นหาบีเวอร์ตัวที่ห้าที่มีงานยุ่ง
ความสำเร็จนี้ไม่เพียงแต่เป็นความท้าทายต่อความเป็นไปไม่ได้ของคณิตศาสตร์เท่านั้น แต่ยังเป็นการสำรวจขีดจำกัดของวิทยาการคอมพิวเตอร์อีกด้วย เมื่อได้รับการยืนยันจาก BB(5) แล้ว นักวิจัยกำลังร่างรายงานทางวิชาการซึ่งจะเป็นเวอร์ชันที่มนุษย์สามารถอ่านได้ ซึ่งจะช่วยเสริมการพิสูจน์ Coq ขณะเดียวกันพวกเขากำลังคิดว่าการสำรวจบีบี(6) จะกลายเป็นเป้าหมายต่อไปหรือไม่
อ้างอิง: https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
การแก้ปัญหาบีเวอร์ที่ยุ่งวุ่นวายไม่เพียงแต่เป็นความก้าวหน้าครั้งสำคัญในสาขาคณิตศาสตร์เท่านั้น แต่ยังให้แนวทางและแนวคิดใหม่ๆ สำหรับการวิจัยทฤษฎีคอมพิวเตอร์ในอนาคตอีกด้วย ความสำเร็จนี้กระตุ้นให้ผู้คนมีส่วนร่วมในการวิจัยคณิตศาสตร์และวิทยาการคอมพิวเตอร์มากขึ้น และสำรวจพื้นที่ที่ไม่รู้จักร่วมกัน