Lanczos下载 - Lanczos源码下载

兰佐斯重采样

介绍

Lanczos（发音为 Lanchos）重采样是一种复杂的数字信号插值技术，与最近邻插值和双线性插值等简单方法相比，可提供卓越的图像质量。通过有效保留细节并最大限度地减少混叠伪影，Lanczos 重采样广泛应用于图像和信号处理应用中。

虽然 Lanczos 在图像质量方面表现出色，但它的代价是计算复杂性增加。此外，潜在的“振铃”伪影（尤其是在锐利边缘周围）可能是一个缺点。尽管面临这些挑战，Lanczos 由于其整体性能优势，仍然是图像缩放和旋转等任务的首选。

本文档全面概述了 Lanczos 重采样，包括其理论基础、实现细节和实际应用。对于寻求理解和利用这种强大技术的开发人员和研究人员来说，它是宝贵的资源。随后的部分深入研究 Lanczos 重采样的关键方面，例如 Lanczos 核、插值和重采样过程、通量保留、上采样、下采样、样本定位、输出范围、多维插值和可分离性。包含一个带有源代码的实际示例。

兰佐斯内核

针对给定支持大小定义的 Lanczos 内核是 Lanczos 重采样中使用的函数。内核定义为：

 L(x) = sinc(x)*sinc(x/a) : -a < x < a
     = 0.0               : otherwise

在哪里：

x 是通过 Lanczos 窗口计算的自变量
a是kernel的支撑尺寸，控制宽度

归一化 sinc 函数定义为：

 sinc(x) = 1.0              : x = 0.0
        = sin(PI*x)/(PI*x) : otherwise

Lanczos3 Kernel

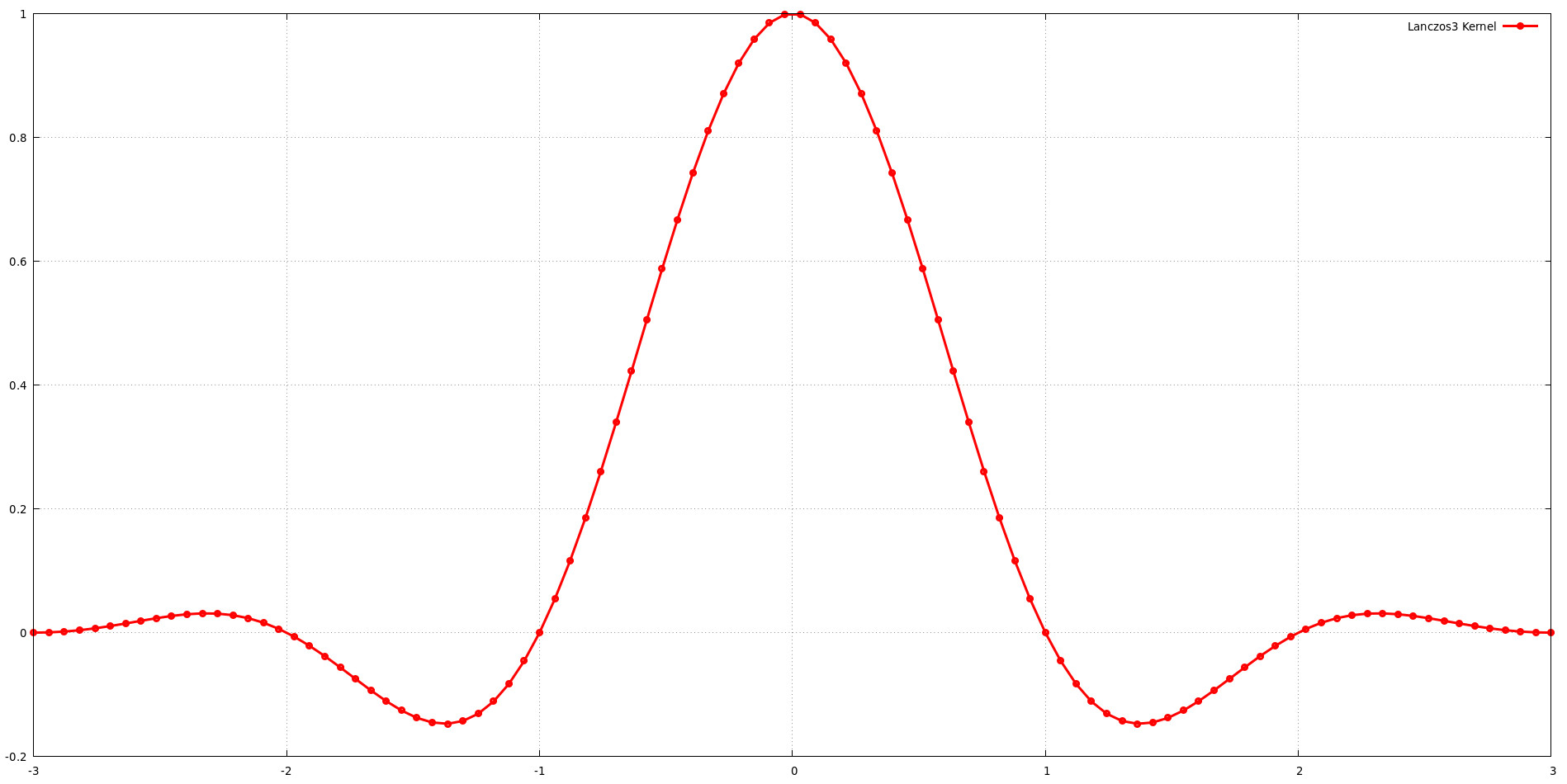
该图说明了支持大小 a = 3 时 Lanczos 核的形状。这意味着该核包括 sinc 函数的三个瓣。虽然增加支撑尺寸 (a) 通常可以为塑造频率响应提供更大的灵活性，但它也会增加计算成本。选择支撑尺寸时，必须在图像质量和计算效率之间取得平衡。 Jim Blinn 发现 a = 3 的 Lanczos 内核在低频保留和高频抑制之间实现了出色的平衡，这支持了这一观点。

注意：术语“内核宽度”、“支持尺寸”和“滤波器尺寸”通常可互换使用来描述参数 a。然而，在 Lanczos 重采样的背景下，“支持大小”最准确地反映了这个概念。

Lanczos 插值和重采样

Lanczos 插值是一种用于将离散信号重新采样到新采样率的技术。它通过将原始信号与 Lanczos 内核进行卷积来实现这一点。

插值信号 s2(x) 可以计算如下：

 s2(x) = (1/w(x))*
        SUM(i = -a + 1, i = a,
            s1(floor(x) + i)*
            L(i - x + floor(x)))

在哪里：

s1(x) 是原始输入信号，视为连续函数
w(x) 是保持通量的归一化因子

保持通量：

归一化因子 w(x) 对于在插值过程中保留整体信号能量或质量至关重要。它确保插值的总和接近原始样本的总和。过滤器重量计算如下：

 w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))

上采样：

当提高采样率时，可以直接使用Lanczos插值方程，无需修改。

下采样：

为了避免降低采样率时出现混叠伪影，必须调整滤波器比例以匹配新的采样率。

 fs = n1/n2

s2(x) = (1/w(x))*
        SUM(i = -(fs*a) + 1, i = (fs*a),
            s1(floor(x) + i)*
            L((i - x + floor(x))/fs))

在哪里：

fs 是下采样因子
n1 是原始信号中的样本数
n2 是插值信号中的样本数

职位示例

将信号从 n1 个样本重采样到 n2 个样本时，将使用以下样本位置。索引j用于表示来自采样信号s2(x)的样本。 (j + 0.5) 项是 s2(x) 中样本的中心。该步骤将 s2(x) 中的点缩放到 s1(x) 中的点。 x 中的最后一项 -0.5 是导致 Lanczos 系数样本偏移的相移。

 step = n1/n2
j    = [0..n2)
x    = (j + 0.5)*step - 0.5

边缘处理

执行 Lanczos 插值时，必须特别注意信号边界。常见的边缘处理技术包括：

零填充：用零将信号扩展到其原始范围之外。
钳位：将边缘值分配给信号边界之外的样本。
镜像：在边界处反射信号。
重复：多次重复边缘值。

零填充：

 s1(x) = s1[floor(x)] : x = [0, n1)
      = 0.0          : otherwise

夹紧：

 s1(x) = s1[clamp(floor(x), 0, n1 - 1)]

钳位通常是首选，因为它可以减少由边缘附近的尖锐不连续性引起的边缘伪影。然而，边缘处理方法的选择取决于具体应用和所需的输出。

输出范围

由于 L(x) 的波瓣，s2(x) 的范围可能大于 s1(x) 的范围。例如，[0.0,1.0]范围内的像素颜色对应的输入信号s1(x)需要钳位到同一范围，以确保转换回[0,255]的无符号字节时输出值不会溢出。

多维插值

Lanczos 核可以扩展到多个维度，以对图像或更高维的数据执行插值。

二维 Lanczos 核定义为：

 L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)

插值信号 s2(x, y) 可以使用以下公式计算：

 s2(x, y) = (1/w(x, y))*
           SUM(i = -a + 1, i = a,
               SUM(j = -a + 1, j = a,
                   s1(floor(x) + j, floor(y) + i)*
                   L(j - x + floor(x), i - y + floor(y))))

其中 w(x, y) 是使用二维 Lanczos 核计算的归一化因子。

可分离性

与某些插值方法不同，Lanczos 核是不可分离的，这意味着它不能分解为一维核的乘积。与可分离内核相比，此属性通常会导致更高的计算成本。为了提高性能，一些实现通过对水平和垂直维度执行单独的传递来近似 Lanczos 内核。

水平插值：

将一维 Lanczos 核应用于输入信号 s1(x, y) 的每一行。
这会产生一个中间结果 s2(x, y)。

垂直插值：

将一维 Lanczos 核应用于中间结果 s2(x, y) 的每一列。
这会产生最终的插值信号 s3(x, y)。

数学表示：

 s2(x, y) = (1/w(x))*
           SUM(j = -a + 1, j = a,
               s1(floor(x) + j, y)*
               L(j - x + floor(x)))

s3(x, y) = (1/w(y))*
           SUM(i = -a + 1, i = a,
               s2(x, floor(y) + i)*
               L(i - y + floor(y)))

请注意，归一化因子 w(x) 和 w(y) 是使用一维 Lanczos 核计算的。

要点：

与全二维 Lanczos 插值相比，可分离近似显着降低了计算成本。
然而，由于 Lanczos 内核不可分离组件的信息丢失，它引入了伪影。
完全 Lanczos 插值和可分离近似之间的选择取决于特定应用对质量和计算效率的要求。

类似地，对信号进行多次递归重采样（通常用于生成纹理 mipmap）也会由于每个重采样步骤的误差累积而降低图像质量。

例子

运行 lancos-test 示例并使用 gnuplot 来查看 Lanczos 重采样在按 2 倍上采样和下采样时如何影响简单的一维信号。

 make
./lanczos-test
gnuplot
> load "output.plot"

Example

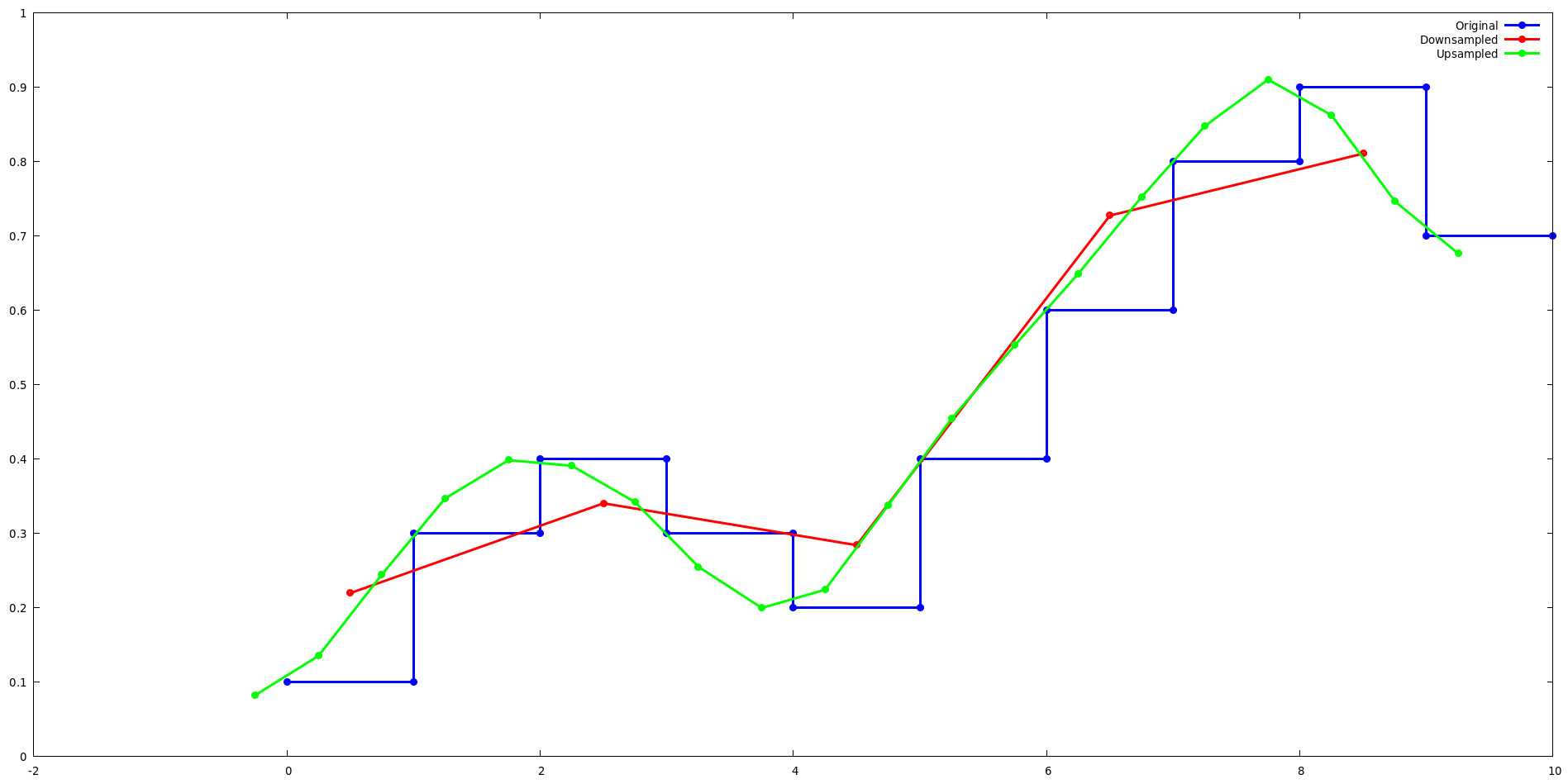
上采样：

当按 2 的幂进行上采样时，Lanczos 内核在 2^level 组值之间循环。例如，考虑 lanzcos-test 上采样示例的前 4 个输出。请注意，L(x) 的输出对于 j={0,2} 和 j={1,3} 重复。

 upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972

下采样：

当按 2 的幂进行下采样时，Lanczos 内核变得独立于 x，因为 (x - Floor(x)) 成为与相移匹配的常数。例如，考虑 lanzcos-test 下采样示例的前 2 个输出。请注意，L(x) 的输出对于每个 j 都是重复的。

 downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943

作为进一步的优化，可以针对这些情况预先计算 Lanczos 内核，以消除昂贵的 sinc 函数计算。

参考

本自述文件是在 Google Gemini 的帮助下创建的。

其他参考资料包括：

兰佐斯重采样
Lanczos 插值和重采样
插值算法
常见重采样任务的过滤器
枕头实施
图像重采样器

执照

该代码由 Jeff Boody 根据 MIT 许可证实现。

 Copyright (c) 2024 Jeff Boody

Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.

展开