GGS

地质勘探局

贪心高斯分割 (GGS) 是一个 Python 求解器，用于有效分割多元时间序列数据。有关实施细节，请参阅我们的论文：http://stanford.edu/~boyd/papers/ggs.html。

---

GGS 求解器采用 n×T 数据矩阵，并将 n 维向量上的 T 个时间戳分成多个片段，在这些片段上，数据可以很好地解释为来自多元高斯分布的独立样本。它通过制定协方差正则化最大似然问题并使用贪心启发式解决该问题来实现这一点，论文中描述了完整的细节。

下载和设置

1. 通过运行以下命令在终端中下载源代码：

 git clone [email protected]:davidhallac/GGS.git

2. 通过运行以下命令确认代码已正确下载：

 cd GGS
python helloworld.py

3. 要编写您自己的使用 ggs 的 Python 函数，只需确保ggs.py与新文件位于同一目录中，然后将以下代码添加到脚本的开头：

 from ggs import *

支持的功能

GGS包具有三个主要功能：

 bps, objectives = GGS(data, Kmax, lamb)

在数据中查找给定正则化参数 lambda 的 K 个断点

输入

data - n×T 数据矩阵，具有 n 维向量的 T 个时间戳

Kmax - 要查找的断点数量

羔羊 - 正则化协方差的正则化参数

退货

bps - 列表的列表，其中较大列表的元素i是 GGS 算法中在K = i处找到的断点集

目标 - 每个中间步骤的目标值列表（ K = 0 到 Kmax）

---

 meancovs = GGSMeanCov(data, breakpoints, lamb)

给定一组断点，查找每个段的均值和正则化协方差。

输入

data - n×T 数据矩阵，具有 n 维向量的 T 个时间戳

断点 - 断点位置列表

羔羊 - 正则化协方差的正则化参数

退货

meancovs - 数据中每个段的（均值、协方差）元组列表

---

 cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])

运行 10 倍交叉验证，并返回每个 (K, lambda) 对的训练集和测试集似然度，最高可达 Kmax

输入

data - n×T 数据矩阵，具有 n 维向量的 T 个时间戳

Kmax - 运行 GGS 的最大断点数

lambdaList - 要测试的正则化参数列表

退货

cvResults -羔羊列表中每个正则化参数的（羔羊，（[TrainLL]，[TestLL]））元组列表。此处，TrainLL 和 TestLL 是从 0 到 Kmax 的所有K的 10 倍交叉验证中的平均每个样本对数似然

---

其他可选参数（对于上述所有三个功能）：

features = [] - 选择数据中的某个列子集进行操作

verbose = False - 运行算法时打印中间步骤

用法示例

运行financeExample.py将生成以下图，显示目标（论文中的公式 4）与断点数量：

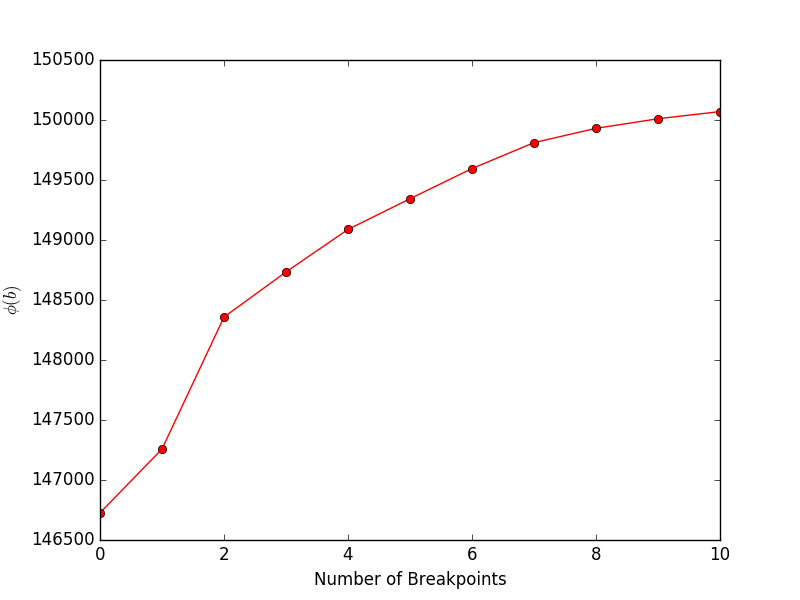
一旦我们解决了断点的位置，我们就可以使用FindMeanCovs()函数来查找每个段的均值和协方差。在helloworld.py的示例中，绘制三个信号的均值、方差和协方差得出：

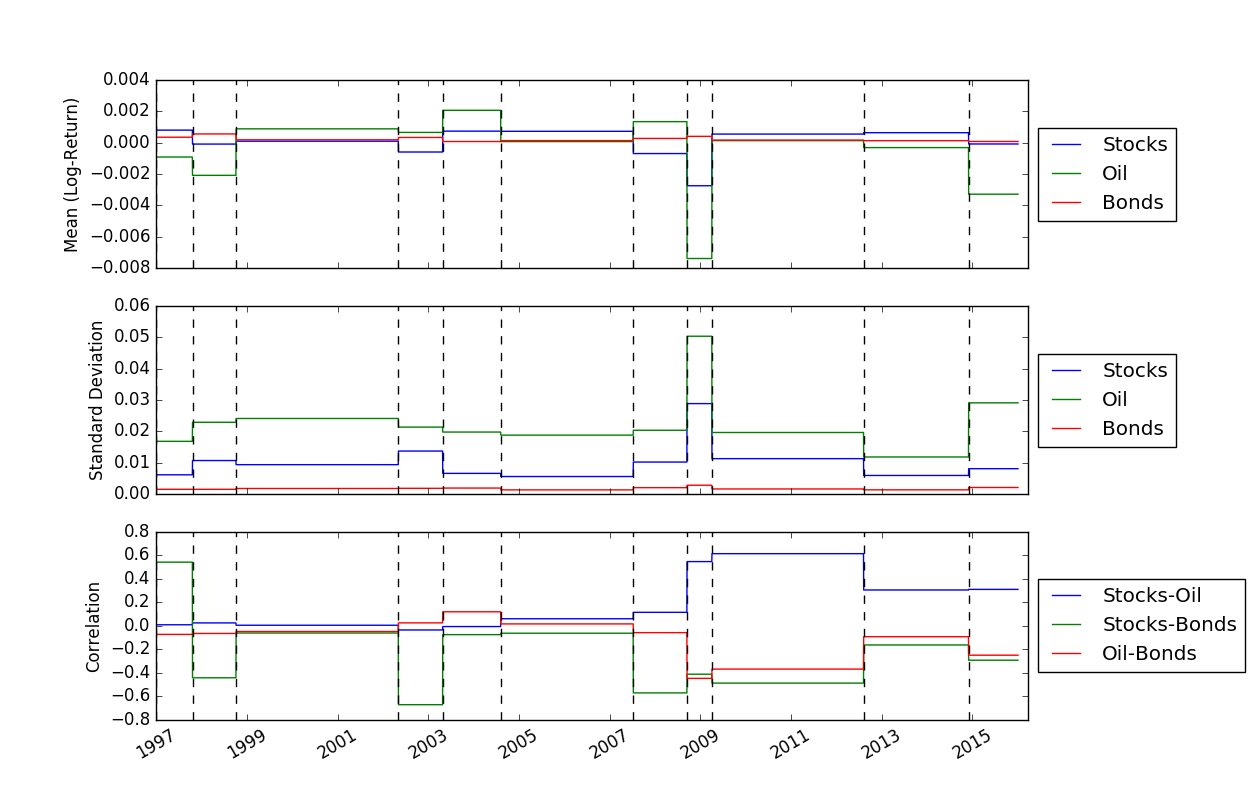
要运行交叉验证（这对于确定 K 和 lambda 的最佳值非常有用），我们可以使用以下代码加载数据，运行交叉验证，然后绘制测试和训练似然：

 from ggs import *
import numpy as np
import matplotlib.pyplot as plt

filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]

#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)

trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()

结果图如下所示：

参考

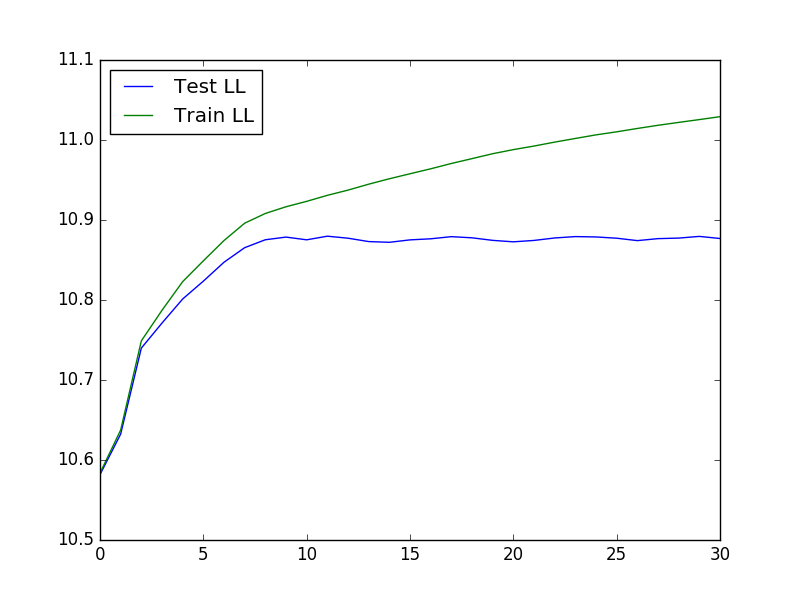
时间序列数据的贪婪高斯分割——D. Hallac、P. Nystrup 和 S. Boyd

作者

大卫·哈拉克、彼得·尼斯特鲁普和斯蒂芬·博伊德。