

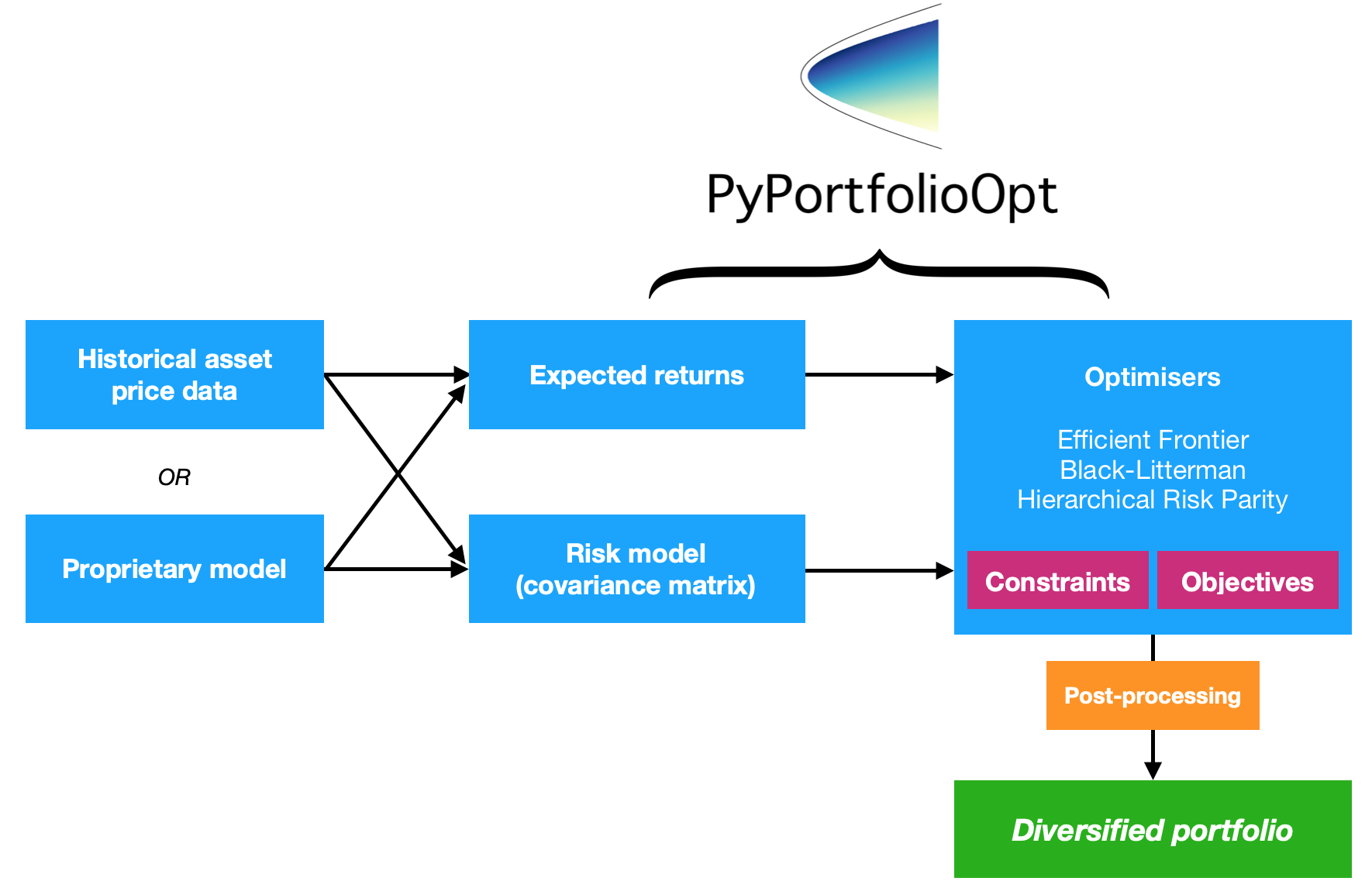
PyPortfolioOpt 是一个实现投资组合优化方法的库,包括经典的均值方差优化技术和 Black-Litterman 分配,以及该领域的最新发展,例如收缩和分层风险平价。
它功能广泛且易于扩展,对于休闲投资者或寻求简单原型设计工具的专业人士来说都非常有用。无论您是一个以基本面为导向、已经确定了一些被低估的选择的投资者,还是一个拥有一揽子策略的算法交易者,PyPortfolioOpt 都可以帮助您以风险有效的方式组合您的阿尔法来源。
PyPortfolioOpt 已发表在《开源软件杂志》上?
PyPortfolioOpt 现在由 Tuan Tran 维护。
请访问ReadTheDocs 上的文档来深入了解该项目,或者查看说明书以查看一些示例,这些示例显示了从下载数据到构建投资组合的完整过程。
如果您想在浏览器中以交互方式使用 PyPortfolioOpt,您可以在此处启动 Binder。设置需要一段时间,但它可以让您尝试食谱,而不必处理所有要求。
注意:macOS 用户需要安装命令行工具。
注意:如果您使用的是 Windows,则首先需要安装 C++。 (下载、安装说明)
该项目可在 PyPI 上使用,这意味着您可以:
pip install PyPortfolioOpt(您可能需要遵循 cvxopt 和 cvxpy 的单独安装说明)。
但是,最佳实践是在虚拟环境中使用依赖项管理器。我目前的建议是让自己熟悉诗歌,然后就跑步
poetry add PyPortfolioOpt否则,克隆/下载项目并在项目目录中运行:
python setup.py install PyPortfolioOpt 支持 Docker。使用docker build -f docker/Dockerfile . -t pypfopt 。您可以使用该映像来运行测试,甚至启动 Jupyter 服务器。
# iPython interpreter:
docker run -it pypfopt poetry run ipython
# Jupyter notebook server:
docker run -it -p 8888:8888 pypfopt poetry run jupyter notebook --allow-root --no-browser --ip 0.0.0.0
# click on http://127.0.0.1:8888/?token=xxx
# Pytest
docker run -t pypfopt poetry run pytest
# Bash
docker run -it pypfopt bash欲了解更多信息,请阅读本指南。
如果您想进行重大更改以将其与您的专有系统集成,则克隆此存储库并仅使用源代码可能是有意义的。
git clone https://github.com/robertmartin8/PyPortfolioOpt或者,您可以尝试:
pip install -e git+https://github.com/robertmartin8/PyPortfolioOpt.git这是一个关于现实生活股票数据的示例,展示了找到最大化夏普比率(风险调整回报的衡量标准)的多头投资组合是多么容易。
import pandas as pd
from pypfopt import EfficientFrontier
from pypfopt import risk_models
from pypfopt import expected_returns
# Read in price data
df = pd . read_csv ( "tests/resources/stock_prices.csv" , parse_dates = True , index_col = "date" )
# Calculate expected returns and sample covariance
mu = expected_returns . mean_historical_return ( df )
S = risk_models . sample_cov ( df )
# Optimize for maximal Sharpe ratio
ef = EfficientFrontier ( mu , S )
raw_weights = ef . max_sharpe ()
cleaned_weights = ef . clean_weights ()
ef . save_weights_to_file ( "weights.csv" ) # saves to file
print ( cleaned_weights )
ef . portfolio_performance ( verbose = True )这会输出以下权重:
{'GOOG': 0.03835,
'AAPL': 0.0689,
'FB': 0.20603,
'BABA': 0.07315,
'AMZN': 0.04033,
'GE': 0.0,
'AMD': 0.0,
'WMT': 0.0,
'BAC': 0.0,
'GM': 0.0,
'T': 0.0,
'UAA': 0.0,
'SHLD': 0.0,
'XOM': 0.0,
'RRC': 0.0,
'BBY': 0.01324,
'MA': 0.35349,
'PFE': 0.1957,
'JPM': 0.0,
'SBUX': 0.01082}
Expected annual return: 30.5%
Annual volatility: 22.2%
Sharpe Ratio: 1.28这很有趣,但其本身并没有什么用处。然而,PyPortfolioOpt 提供了一种方法,允许您将上述连续权重转换为您可以购买的实际分配。只需输入最新价格和所需的投资组合规模(本例中为 10,000 美元):
from pypfopt . discrete_allocation import DiscreteAllocation , get_latest_prices
latest_prices = get_latest_prices ( df )
da = DiscreteAllocation ( weights , latest_prices , total_portfolio_value = 10000 )
allocation , leftover = da . greedy_portfolio ()
print ( "Discrete allocation:" , allocation )
print ( "Funds remaining: ${:.2f}" . format ( leftover ))12 out of 20 tickers were removed
Discrete allocation: {'GOOG': 1, 'AAPL': 4, 'FB': 12, 'BABA': 4, 'BBY': 2,
'MA': 20, 'PFE': 54, 'SBUX': 1}
Funds remaining: $ 11.89免责声明:本项目不构成投资建议,作者对您后续的投资决策不承担任何责任。请参阅许可证以获取更多信息。
Harry Markowitz 1952 年的论文是不可否认的经典,它将投资组合优化从一门艺术变成了一门科学。关键的见解是,通过将具有不同预期收益和波动性的资产组合起来,人们可以决定一种数学上的最优配置,从而最大限度地降低目标收益的风险——所有此类最优投资组合的集合被称为有效前沿。
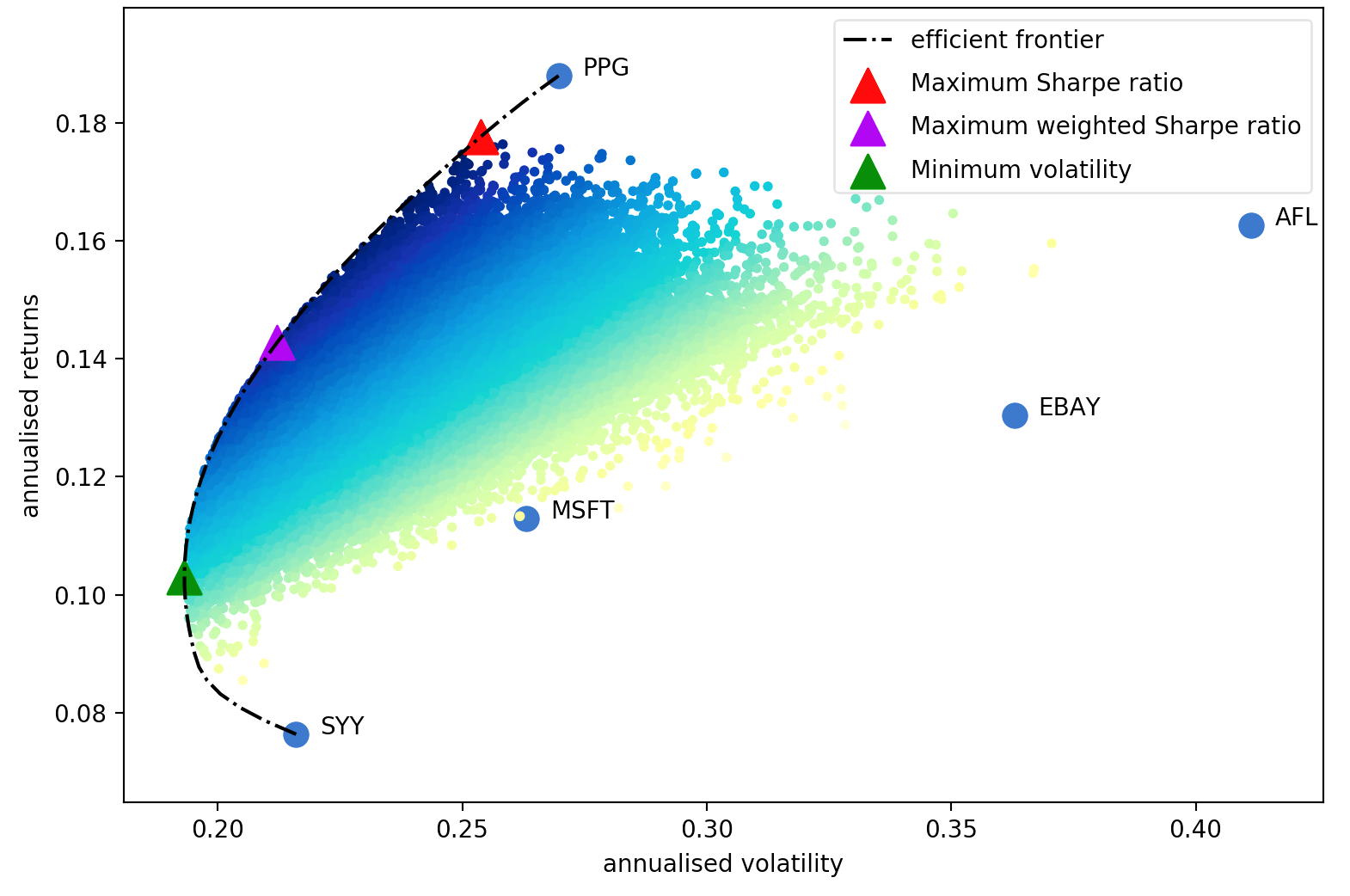
尽管该主题已经取得了很大的发展,但半个多世纪后,马科维茨的核心思想仍然具有根本性的重要意义,并且在许多投资组合管理公司中得到日常应用。均值方差优化的主要缺点是理论处理需要了解资产的预期收益和未来风险特征(协方差)。显然,如果我们知道股票的预期回报,生活会容易得多,但整个游戏是股票回报很难预测。相反,我们可以根据历史数据得出预期回报和协方差的估计——尽管我们确实失去了马科维茨提供的理论保证,但我们的估计越接近实际值,我们的投资组合就越好。
因此,这个项目提供了四组主要的功能(尽管它们当然是密切相关的)
PyPortfolioOpt 的一个关键设计目标是模块化——用户应该能够交换其组件,同时仍然使用 PyPortfolioOpt 提供的框架。
在本节中,我们将详细介绍 PyPortfolioOpt 的一些可用功能。此处的 Jupyter 笔记本中提供了更多示例。另一个好的资源是测试。
可以在 ReadTheDocs 上找到更全面的版本,以及针对更高级用户的可能扩展。
协方差矩阵不仅编码资产的波动性,还编码它与其他资产的相关性。这很重要,因为为了获得多元化的好处(从而增加单位风险的回报),投资组合中的资产应尽可能不相关。
sklearn.covariance提供的高效矢量化实现的包装器。constant_variance 、 single_factor和constant_correlation 。sklearn.covariance中实现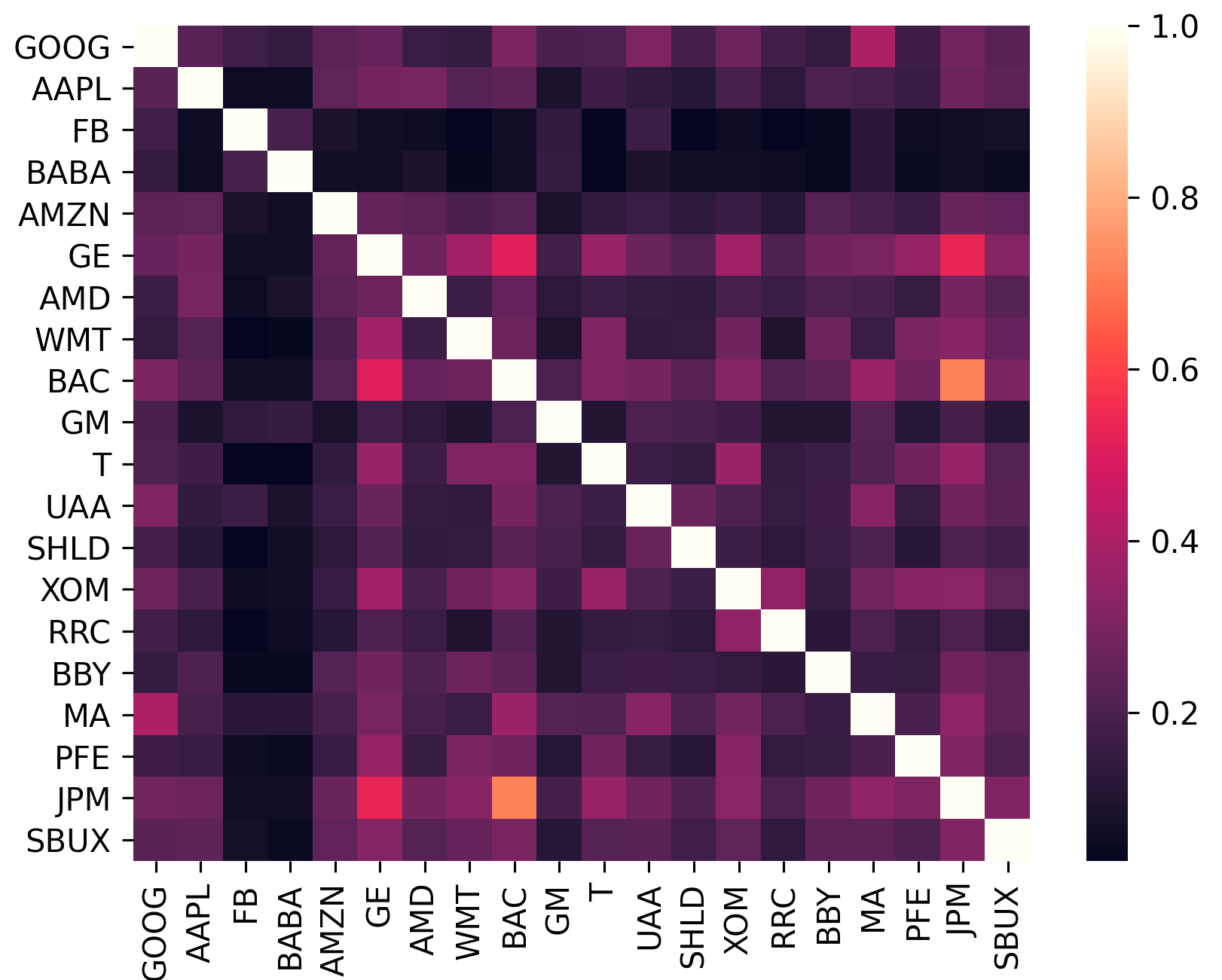
(该图是使用plotting.plot_covariance生成的)
ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))efficient_risk和efficient_return方法,PyPortfolioOpt提供了形成市场中性投资组合的选项(即权重总和为零)。这对于最大夏普投资组合和最小波动率投资组合来说是不可能的,因为在这些情况下,它们对于杠杆而言不是不变的。市场中性需要负权重: ef = EfficientFrontier ( mu , S , weight_bounds = ( - 1 , 1 ))
ef . efficient_return ( target_return = 0.2 , market_neutral = True ) ef = EfficientFrontier ( mu , S , weight_bounds = ( 0 , 0.1 ))均值方差优化的一个问题是它会导致许多零权重。虽然这些在样本内是“最佳”的,但大量研究表明,这一特征导致均值方差投资组合的表现低于样本外。为此,我引入了一个目标函数,它可以减少任何目标函数的可忽略权重的数量。本质上,它在小权重上添加了惩罚(由gamma参数化),这个术语看起来就像机器学习中的 L2 正则化。可能需要尝试多个gamma值才能获得所需数量的不可忽略的权重。对于 20 种证券的测试组合, gamma ~ 1就足够了
ef = EfficientFrontier ( mu , S )
ef . add_objective ( objective_functions . L2_reg , gamma = 1 )
ef . max_sharpe ()从 v0.5.0 开始,我们现在支持 Black-Litterman 资产配置,它允许您将先前的回报估计(例如市场隐含回报)与您自己的观点相结合,形成后验估计。与仅使用平均历史回报相比,这可以更好地估计预期回报。查看文档以获取理论讨论以及有关格式化输入的建议。
S = risk_models . sample_cov ( df )
viewdict = { "AAPL" : 0.20 , "BBY" : - 0.30 , "BAC" : 0 , "SBUX" : - 0.2 , "T" : 0.131321 }
bl = BlackLittermanModel ( S , pi = "equal" , absolute_views = viewdict , omega = "default" )
rets = bl . bl_returns ()
ef = EfficientFrontier ( rets , S )
ef . max_sharpe ()上述功能主要涉及通过二次规划解决均值方差优化问题(尽管这是由cvxpy处理的)。但是,我们也提供不同的优化器:
请参阅文档了解更多信息。
测试是用 pytest 编写的(在我看来,比unittest和变体更直观),并且我试图确保接近 100% 的覆盖率。通过导航到包目录并简单地在命令行上运行pytest来运行测试。
PyPortfolioOpt 提供了 20 个股票每日收益的测试数据集:
[ 'GOOG' , 'AAPL' , 'FB' , 'BABA' , 'AMZN' , 'GE' , 'AMD' , 'WMT' , 'BAC' , 'GM' ,
'T' , 'UAA' , 'SHLD' , 'XOM' , 'RRC' , 'BBY' , 'MA' , 'PFE' , 'JPM' , 'SBUX' ]这些股票经过非正式选择,以满足以下几个标准:
目前,测试尚未探索所有边缘情况以及目标函数和参数的组合。然而,每种方法和参数都经过测试,可以按预期工作。
如果您使用 PyPortfolioOpt 来发表作品,请引用 JOSS 论文。
引文字符串:
Martin, R. A., (2021). PyPortfolioOpt: portfolio optimization in Python. Journal of Open Source Software, 6(61), 3066, https://doi.org/10.21105/joss.03066
书目索引::
@article { Martin2021 ,
doi = { 10.21105/joss.03066 } ,
url = { https://doi.org/10.21105/joss.03066 } ,
year = { 2021 } ,
publisher = { The Open Journal } ,
volume = { 6 } ,
number = { 61 } ,
pages = { 3066 } ,
author = { Robert Andrew Martin } ,
title = { PyPortfolioOpt: portfolio optimization in Python } ,
journal = { Journal of Open Source Software }
}非常欢迎您的贡献。请参阅贡献指南了解更多信息。
我要感谢自 2018 年发布以来为 PyPortfolioOpt 做出贡献的所有人员。特别感谢: