Dropout NeuralNetworks

Dropout：防止神经网络过度拟合的简单方法

在这个研究项目中，我将重点关注改变辍学率对 MNIST 数据集的影响。我的目标是用研究论文中使用的数据重现下图。该项目的目的是了解机器学习图形是如何生成的。具体来说，了解更改/不更改丢失概率时对分类错误的影响。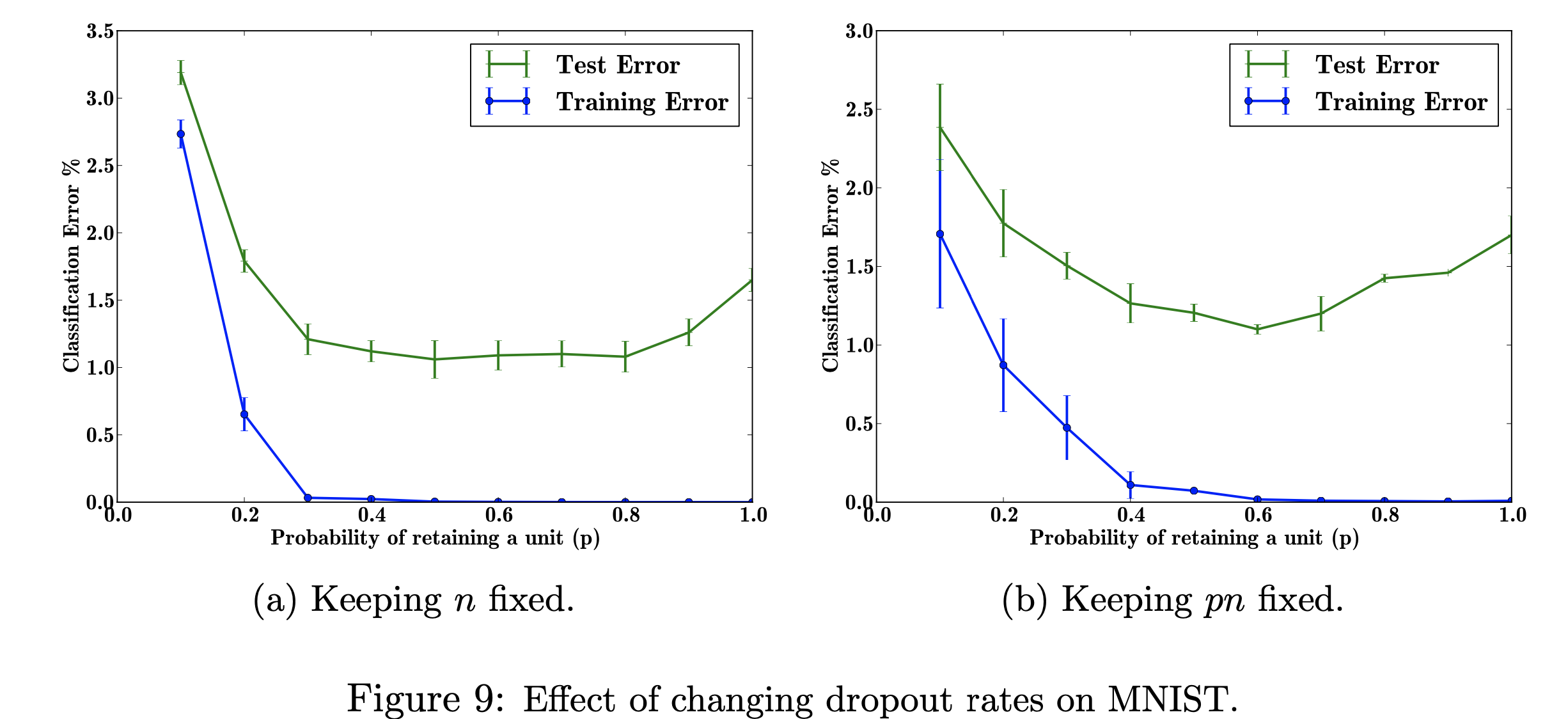图参考自：Srivastava, N.、Hinton, G.、Krizhevsky, A.、Krizhevsky, I.、Salakhutdinov, R.，Dropout：防止神经网络过拟合的简单方法，图 9

如何重现分析：

• 必须安装 python 2.7.X
• 在终端中使用命令“make”
• 最好在 UNIX/Linux 环境中运行

使用的软件/库

我使用 TensorFlow 在 MNIST 数据集上运行 dropout，使用 Matplotlib 来帮助重新创建论文中的图形。我还使用内置的 Decimal 库来计算 p 的不同值，从 0.0 到 1.0。导入库“csv”用于将之前运行的数据添加到 CSV 文件中，以节省计算已计算的 p 值的时间。导入 Numpy 是为了使绘图在 x 轴和 y 轴上具有相同的步长。最后，我导入了“os”，这样我就可以消除由于使用 CPU 而不是 GPU 导致的错误。

编码项目的目的：

探索可调超参数“p”（在网络中保留单元的概率）和隐藏层数量“n”的不同值对错误率的影响。当 p 和 n 的乘积固定时，我们可以看到，与保持隐藏层数量不变（图 9b）相比，小 p 值的误差幅度有所减小（图 9a）。

问题设置：

由于训练数据有限，输入/输出之间的许多复杂关系将是采样噪声的结果。它们将存在于训练集中，但不会存在于真实的测试数据中，即使它是从相同的分布中提取的。这种复杂性会导致过度拟合，这是有助于防止这种情况发生的算法之一。该图的输入是手写数字的数据集，添加 dropout 后的输出是描述应用 dropout 方法的结果的不同值。总而言之，添加 dropout 后错误会减少。

数据来源：

这可以适用的一个现实世界问题是谷歌搜索，有人可能正在搜索电影标题，但他们可能只是在寻找图像，因为他们是更多的视觉学习者。因此，删除文本部分或简短的解释将帮助您专注于图像特征。文章指出了他们从何处检索数据 (http://yann.lecun.com/exdb/mnist/)。每个图像都是 28x28 数字表示。 y 标签似乎是图像数据列。

算法：

我重现该图的目标是测试/训练数据并计算每个概率 p（在网络中保留单元的概率）的分类误差。我的目标是让 p 随着误差的下降而增加，以表明我的实现是有效的，并且我将调整这个超参数以获得相同的结果。我将通过使用 784-2048-2048-2048-10 架构循环遍历所有训练和测试数据来完成此操作，并保持 n 固定，然后更改 pn 进行固定。然后我会将数据收集/写入 csv 文件。然后，该 csv 文件将包含输出图形所需的所有数据。在这个项目中，我将了解丢失率如何有利于神经网络中的整体误差。

项目建议：

点击查看