首页|安装|文档|教程|开发商
rodeo是一个快速的 Python 库,它使用概率数值来求解常微分方程 (ODE)。也就是说,大多数 ODE 求解器(例如欧拉方法)会在步长网格上生成 ODE 的确定性近似值
rodeo为许多概率求解器常见的非线性贝叶斯过滤范例提供了轻量级且可扩展的近似系列(Tronarp 等人(2018))。首先将高斯过程置于 ODE 解的前面,并在求解器逐步遍历网格时按顺序更新它。 rodeo基于jax构建,允许即时编译和自动微分。 jax的 API 几乎等同于numpy的 API。
rodeo提供了两种主要工具:一种用于近似 ODE 解,另一种用于参数推断。对于前者我们提供:
solve :使用非线性贝叶斯过滤范例的概率 ODE 求解器的实现。对于后者,我们提供似然近似方法:
basic :基本似然近似方法的实现(详细信息可以在 Wu 和 Lysy (2023) 中找到)。fenrir :Fenrir 的实现(Tronarp 等人(2022))。marginal_mcmc :Chkrebtii 方法的 MCMC 实现(Chkrebtii 等人(2016))。dalton :数据自适应 ODE 似然近似的实现(Wu 和 Lysy (2023))。其使用的详细示例可以在文档部分找到。请注意,这是rodeo的仅jax版本。对于使用各种其他后端的旧版本,请参阅此处。
从 GitHub 下载存储库,然后使用setup.cfg脚本进行安装:
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . 请首先转到 readthedocs 查看以下示例的渲染文档。
有关解决简单 ODE 问题的快速入门教程。
求解高阶 ODE 的示例。
求解困难的混沌 ODE 的示例。
我们使用拉普拉斯近似的参数推断问题的示例。
在本演练中,我们展示了如何使用概率求解器求解 ODE 并进行参数推断。我们将首先说明求解 ODE 的设置。为此,我们考虑以下一阶 ODE 示例( FitzHugh-Nagumo模型),
解决方案在哪里
根据 (Wu and Lysy (2023)) 的记号,我们有
为了
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
)我们将求解器的解与scipy库中odeint提供的确定性解进行比较。
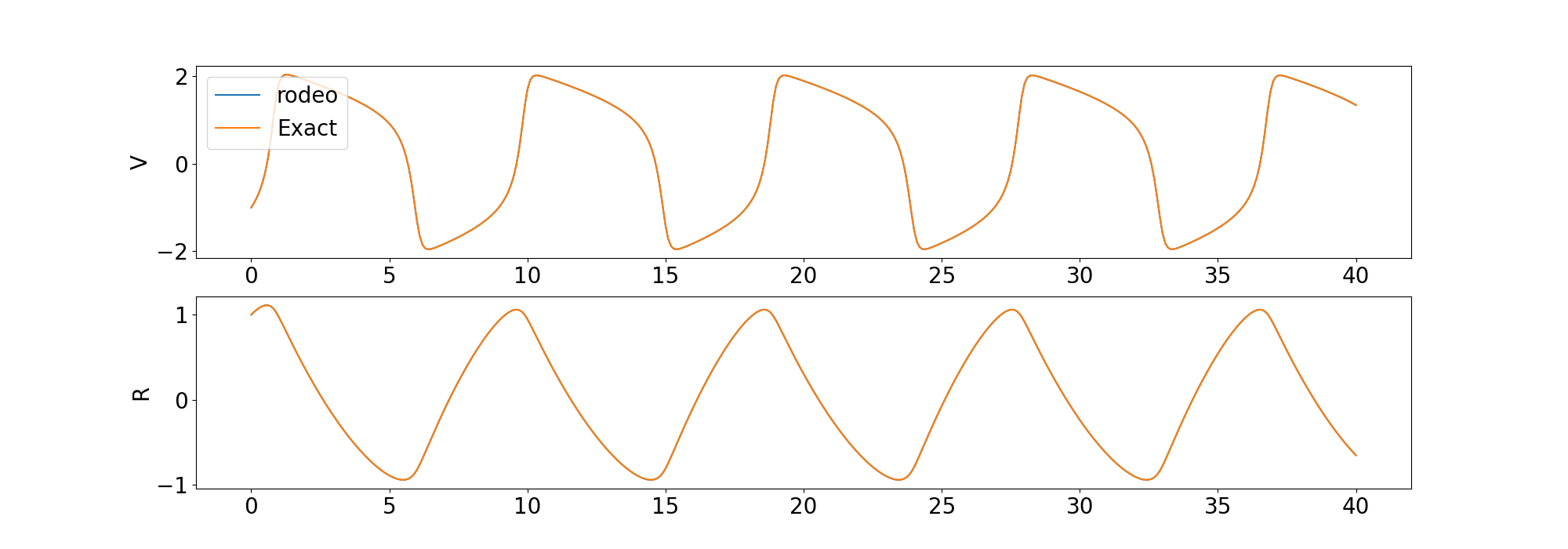
我们还提供了求解高阶 ODE 和混沌 ODE 的示例。
我们现在转向参数推断问题。 rodeo包含描述部分中总结的几种似然近似方法。在这里,我们将使用basic似然近似方法。假设通过模型模拟观察结果
在哪里basic似然近似
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars ))这是演示用法的基本示例。我们建议使用更复杂的似然近似,将解的不确定性传播到似然近似,例如fenrir 、 marginal_mcmc和dalton 。更多详情请参考参数推断教程。
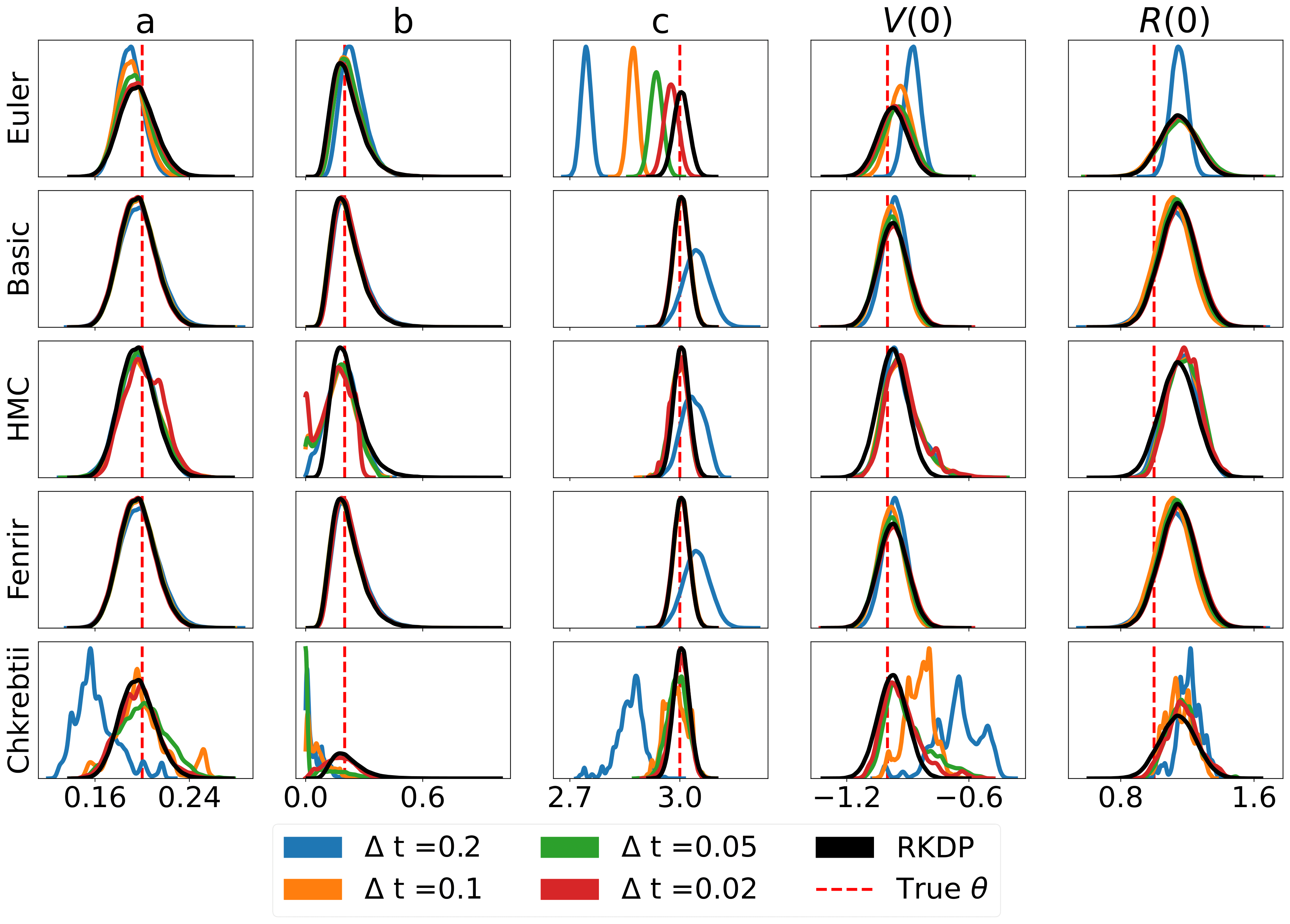
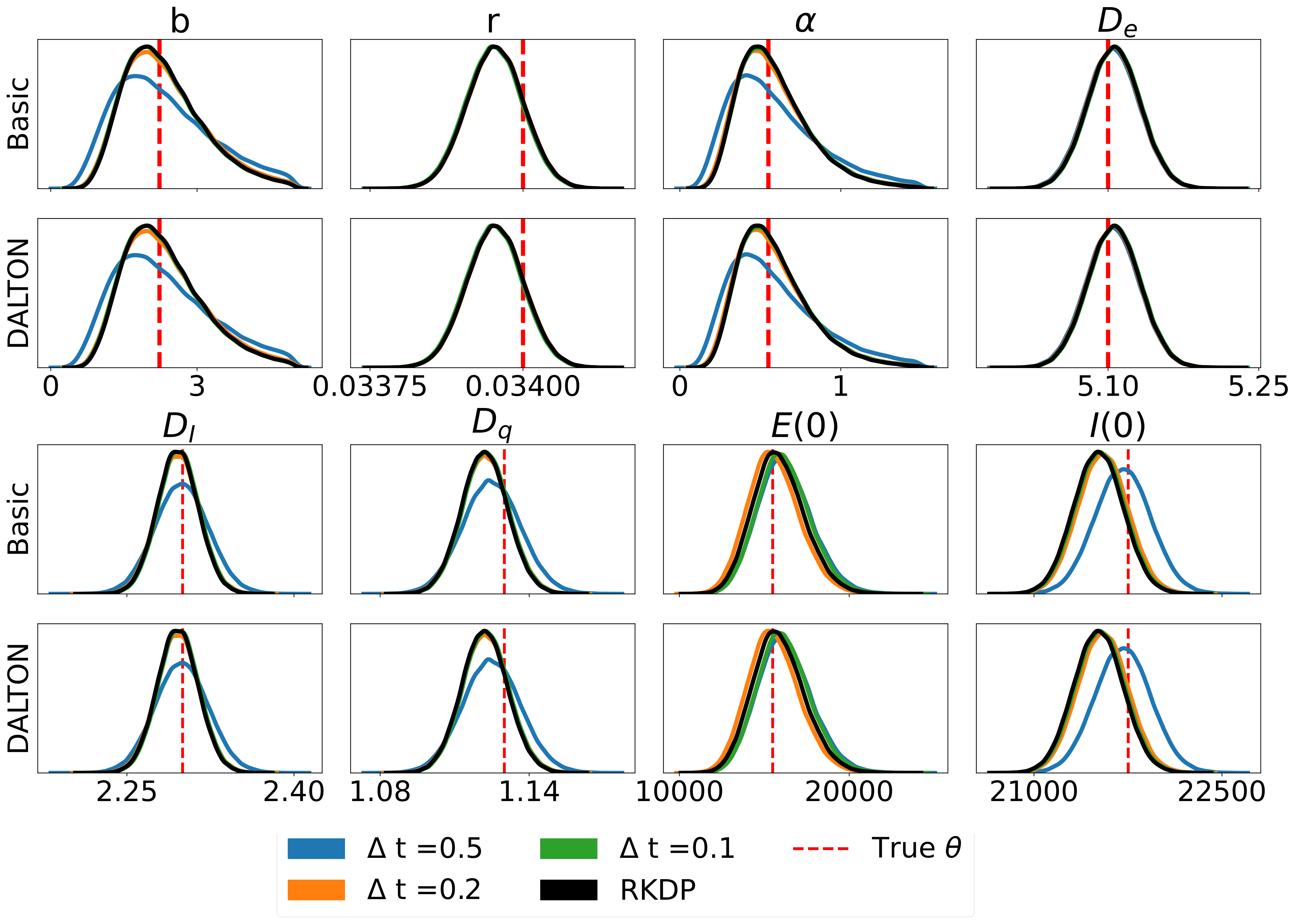
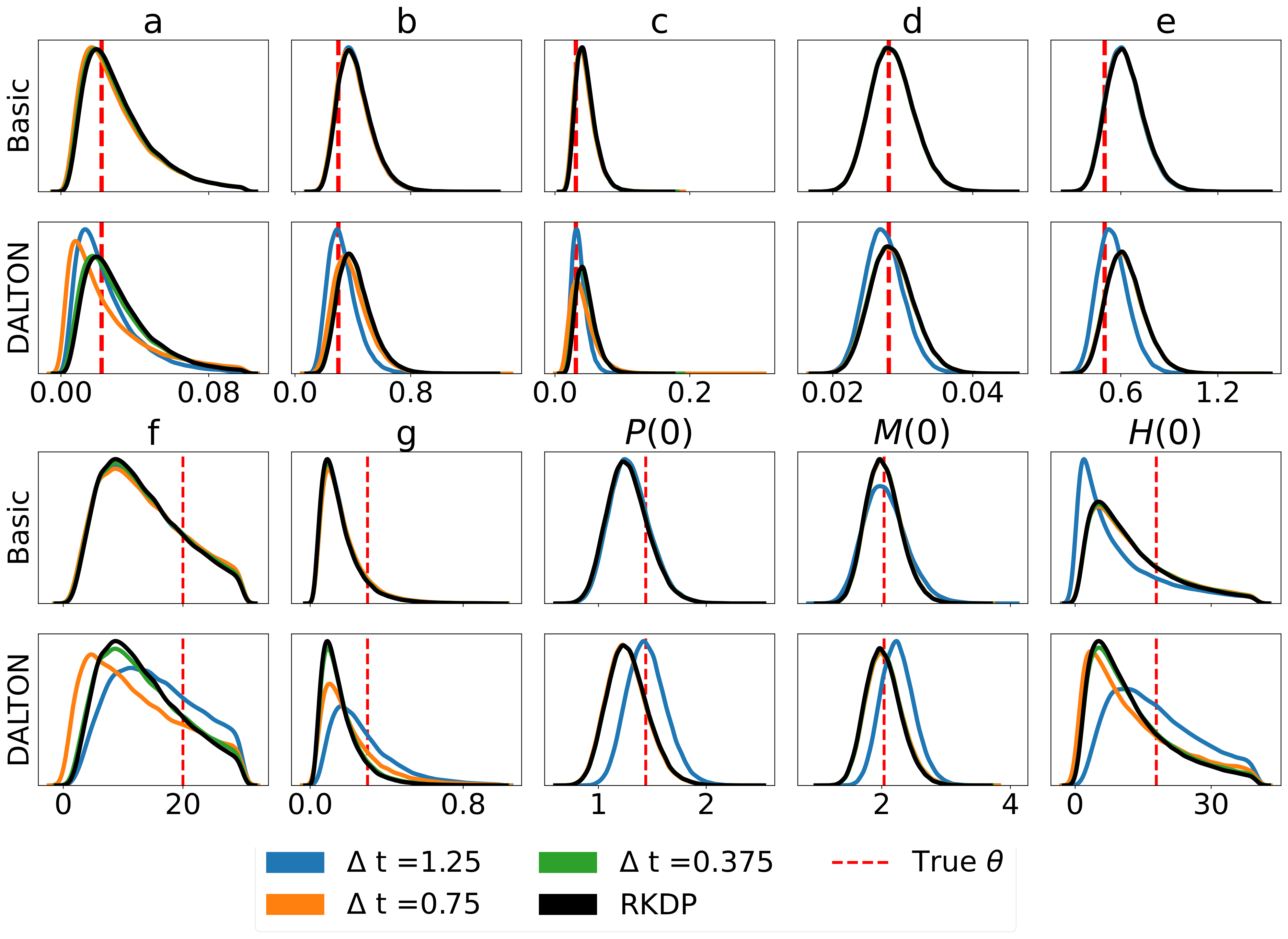
以下是/examples/中在rodeo中发现的各种似然近似产生的一些结果:
可以通过以下命令运行单元测试:
cd tests
python -m unittest discover -v或者,安装tox ,然后从rodeo中输入命令行: tox 。
HTML 文档可以从根文件夹编译:
pip install .[docs]
cd docs
make html这将在docs/build中创建文档。